Что такое остовное дерево

Остовное дерево

Остовное дерево связного неориентированного графа — ациклический связный подграф данного графа, в который входят все его вершины. Неформально говоря, остовное дерево состоит из некоторого подмножества рёбер графа, таких, что из любой вершины графа можно попасть в любую другую вершину, двигаясь по этим рёбрам, и в нём нет циклов, то есть из любой вершины нельзя попасть в саму себя, не пройдя какое-то ребро дважды.

Понятие остовный лес неоднозначно, под ним могут понимать один из следующих подграфов:

Остовное дерево также иногда называют покрывающим деревом, остовом или скелетом графа. Ударение в слове «остовный» у разных авторов указывается на первый [1] (от слова о́стов) или на второй слог.

Содержание

Свойства

Алгоритмы

Остовное дерево может быть построено практически любым алгоритмом обхода графа, например поиском в глубину или поиском в ширину. Оно состоит из всех пар рёбер , таких, что алгоритм, просматривая вершину обнаруживает в её списке смежности новую, не обнаруженную ранее вершину .

Остовные деревья, построенные при обходе графа алгоритмом Дейкстры, начиная из вершины , обладают тем свойством, что кратчайший путь в графе из до любой другой вершины — это (единственный) путь из до этой вершины в построенном остовном дереве.

Существует также несколько параллельных и распределённых алгоритмов нахождения остовного дерева. Как практический пример распределённого алгоритма можно привести протокол STP.

Если каждому ребру графа присвоен вес (длина, стоимость и т. п.), то нахождением оптимального остовного дерева, которое минимизирует сумму весов входящих в него рёбер, занимаются многочисленные алгоритмы нахождения минимального остовного дерева.

Задача о нахождении остовного дерева, в котором степень каждой вершины не превышает некоторой наперёд заданной константы , является NP-полной. [3]

См. также

Примечания

Полезное

Смотреть что такое «Остовное дерево» в других словарях:

остовное дерево — Метод, используемый в стандарте IEEE 802.1 для обнаружения и исключения логических петель в сетях с мостами или коммутаторами. При наличии нескольких путей алгоритм STP конфигурирует сеть так, чтобы использовался единственный путь (наиболее… … Справочник технического переводчика

Минимальное остовное дерево — (или минимальное покрывающее дерево) в связанном, взвешенном, неориентированном графе это остовное дерево этого графа, имеющее минимальный возможный вес, где под весом дерева понимается сумма весов входящих в него рёбер. Содержание 1 Пример … Википедия

алгоритм SpanningTree (остовное дерево) — Алгоритм, используемый для обеспечения в каждый момент времени единственного пути между любыми двумя станциями многосвязной ЛВС. Метод определения наилучшего пути между станциями в многосвязной сети с мостами. … … Справочник технического переводчика

Дерево (теория графов) — У этого термина существуют и другие значения, см. Дерево (значения). Дерево это связный ациклический граф.[1] Связность означает наличие путей между любой парой вершин, ацикличность отсутствие циклов и то, что между парами вершин… … Википедия

Дерево (граф) — В теории графов, дерево связный (ориентированный или неориентированный) граф, не содержащий циклов (для любой вершины есть один и только один способ добраться до любой другой вершины). Древовидная структура тип организации, в котором каждый… … Википедия

ДЕРЕВО — в теории графов связный неориентированный граф G, не содержащий циклов. Д. не имеет кратных ребер и петель. Являясь простейшими связными графами, Д. служат хорошими моделями для рассмотрения различных вопросов теории графов. Любое Д. с пвершинами … Математическая энциклопедия

Список алгоритмов — Эта страница информационный список. Основная статья: Алгоритм Ниже приводится список алгоритмов, группированный по категориям. Более детальные сведения приводятся в списке структур данных и … Википедия

Программируемые алгоритмы — Служебный список статей, созданный для координации работ по развитию темы. Данное предупреждение не устанавл … Википедия

Алгоритм Крускала — (или алгоритм Краскала) алгоритм построения минимального остовного дерева взвешенного связного неориентированного графа. Алгоритм впервые описан Джозефом Крускалом в 1956 году. Содержание 1 Формулировка 2 Оценка … Википедия

ГРАФОВ ТЕОРИЯ — в химии, область конечной математики, изучающая дискретные структуры, наз. графами; применяется для решения различных теоретич. и прикладных задач. Некоторые основные понятия. Граф совокупность точек (вершин) и совокупность пар этих точек (не… … Химическая энциклопедия

Источник

Алгоритм Краскала, Прима для нахождения минимального остовного дерева

Привет, Хабр!
В свободное от учебы время пишу статьи, которых мне не хватало несколько лет назад.

Алгоритмы нахождения MST применимы в различных областях, начиная от кластеризации данных до построения компьютерных, транспортных сетей.
Я надеюсь, что вы после прочтения данной статьи, примерно понимали, как работают жадные алгоритмы нахождения MST.

Формальная постановка задачи

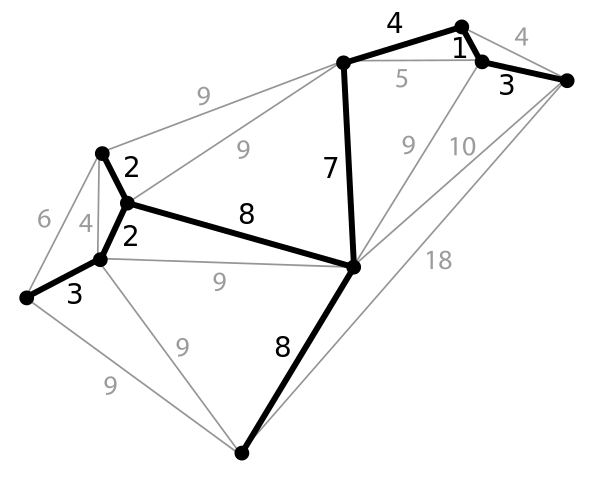
Имеется следующий неориентированный взвешенный граф. Назовем остовным деревом подграф, содержащий все вершины исходного графа, который является деревом. И задача состоит в том, чтобы найти такое остовное дерево, сумма рёбер которого минимальна.

Исходный граф

Неформальная постановка задачи

Представьте исходный граф без рёбер, теперь вам нужно как-то соединить все вершины между собой, чтобы можно было бы попасть из любой вершины в другую, не имея при этом циклов в получившемся графе с минимально возможной суммой весов включенных рёбер.

Алгоритм Краскала

Механизм, по которому работает данный алгоритм, очень прост. На входе имеется пустой подграф, который и будем достраивать до потенциального минимального остовного дерева. Будем рассматривать только связные графы, в другом случае при применении алгоритма Краскала мы будем получать не минимальное остовное дерево, а просто остовной лес.

Вначале мы производим сортировку рёбер по неубыванию по их весам.

Алгоритм завершит свою работу после того, как множество вершин нашего подграфа совпадет с множеством вершин исходного графа.

Данный алгоритм называется жадным из-за того, что мы на каждом шаге пытаемся найти оптимальный вариант, который приведет к оптимальному решению в целом.

Разбор конкретного примера по шагам

Из представленного сверху графа, выпишем все его ребра в отсортированном порядке:

1) D B; w = 2
2) D C; w = 6
3) A B; w = 7
4) A C; w = 8
5) C E; w = 9
6) D F; w = 9
7) F E; w = 10
8) B C; w = 11
9) D E; w = 11

И начнем по списку добавлять эти ребра в наш остов:

Подграф после добавиления 1-го ребра Подграф после добавления 2-го и 3-го рёбер

При добавлении в наше остовное дерево ребра A C, как вы можете заметить, образовывается цикл, поэтому мы просто пропускаем данное ребро.

По итогу у нас образовывается следующий подграф, и как вы заметили, мы соединили все вершины ребрами с минимально-возможными весами, а значит, нашли минимальное остовное дерево для нашего исходного графа.

Минимальный остов

Проводим проверку с помощью встроенного алгоритма для нахождения MST на graphonline, и видим, что подграфы идентичны.
И да, из-за того, что при равенстве весов рёбер мы можем выбрать любое из них, конечные подграфы, являющиеся минимальными остовными деревьями, могут различаться с точностью до некоторых рёбер.

Провели проверку

Суммарный вес искомого MST равен 33.

Реализация

Реализовать представленный алгоритм проще всего с помощью СНМ(система непересекающихся отрезков).

Вначале, как мы уже раннее говорили, необходимо отсортировать ребра по неубыванию по их весам. Далее с помощью вызовов функции make_set() мы каждую вершину можем поместить в свое собственное дерево, то есть, создаем некоторое множество подграфов. Дальше итерируемся по всем ребрам в отсортированном порядке и смотрим, принадлежат ли инцидентные вершины текущего ребра разным подграфам с помощью функции find_set() или нет, если оба конца лежат в разных компонентах, то объединяем два разных подграфа в один с помощью функции union_sets().

В итоге асимптотическая сложность данного алгоритма сводится к:

Алгоритм Прима

Суть самого алгоритма Прима тоже сводится к жадному перебору рёбер, но уже из определенного множества. На входе так же имеется пустой подграф, который и будем достраивать до потенциального минимального остовного дерева.

Изначально наш подграф состоит из одной любой вершины исходного графа.

Затем из рёбер инцидентных этой вершине, выбирается такое минимальное ребро, которое связала бы две абсолютно разные компоненты связности, одной из которых и является наш подграф. То есть, как только у нас появляется возможность добавить новую вершину в наш подграф, мы тут же включаем ее по минимальмально возможному весу.

Продолжаем выполнять предыдущий шаг до тех пор, пока не найдем искомое MST.

Разбор конкретного примера

Выбираем чисто случайно вершину E, далее рассмотрим все ребра исходящие из нее, включаем в наше остовное дерево ребро C E; w = 9, так как данное ребро имеет минимальный вес из всех рёбер инцидентных множеству вершин нашего подграфа. Имеем следующее:

Подграф после добавления 1-го ребра

Теперь выборка производится из рёбер:
D C; w = 6
A C; w = 8
F E; w = 10
B C; w = 11
D E; w = 11

То есть, в данный момент, мы знаем только о двух вершинах, соответственно, знаем о всех ребрах, исходящих из них. Про связи между другими вершинами, которые не включены в наш подграф, мы ничего не знаем, поэтому они на этом шаге не рассматриваются.

Подграф, полученный после добавления рассмотренных рёбер

Давайте добьем наш подграф до минимального остовного дерева. Вы, наверное, уже догадались о том, по каким ребрам мы будем связывать наши оставшиеся вершины:
A и F.

Искомое минимальное остовное дерево

Суммарный вес искомого MST равен 33.

Источник

Минимальное остовное дерево. Алгоритм Прима. Алгоритм Крускала

Минимальное остовное дерево

Остовным деревом графа называется дерево, которое можно получить из него путём удаления некоторых рёбер. У графа может существовать несколько остовных деревьев, и чаще всех их достаточно много.

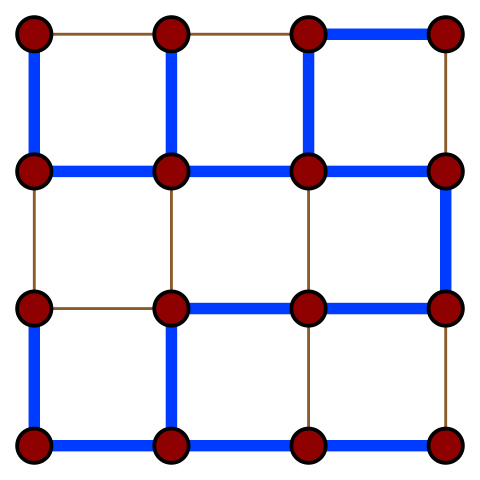
На иллюстрации приведено одно из остовных деревьев (рёбра выделены синим цветом) решёткообразного графа.

Для нахождения минимального остовного дерева графа существуют два основных алгоритма: алгоритм Прима и алгоритм Крускала. Они оба имеют сложность \(O(M \log N)\), поэтому выбор одного из них зависит от ваших личных предпочтений. В этой лекции мы разберём оба.

Алгоритм Прима

Алгоритм Прима в идее и реализации очень похож на алгоритм Дейкстры. Как и в алгоритме Дейкстры, мы поддерживаем уже обработанную часть графа (минимального остовного дерева), и постепенно её расширяем за счёт ближайших вершин.

Утверждается, что если разделить вершины графа на два множества (обработанные и необработанные), первое из которых составляет связную часть минимального остовного дерева, то ребро минимальной длины, связывающее эти два множества гарантированно будет входить в минимальное остовное дерево.

Таким образом, для нахождения минимального остовного дерева начнём с произвольной вершины и будем постепенно добавлять ближайшие к уже имеющимся.

Реализация алгоритма Прима

Будем искать вес минимального остовного дерева. Для нахождения ближайшей вершины воспользуемся очередью с приоритетом (аналогично алгоритму Дейкстры), в которой будем хранить пары (расстояние от остова до вершины, номер вершины).

Алгоритм Крускала

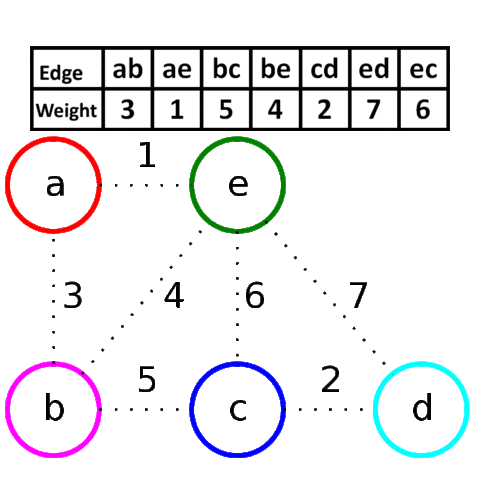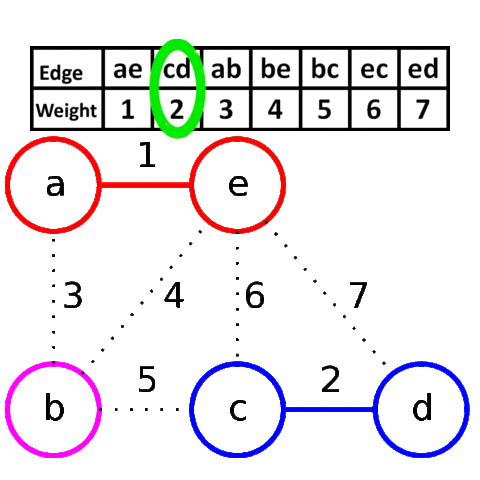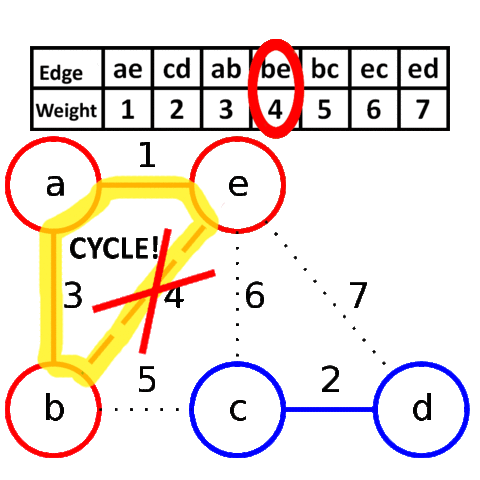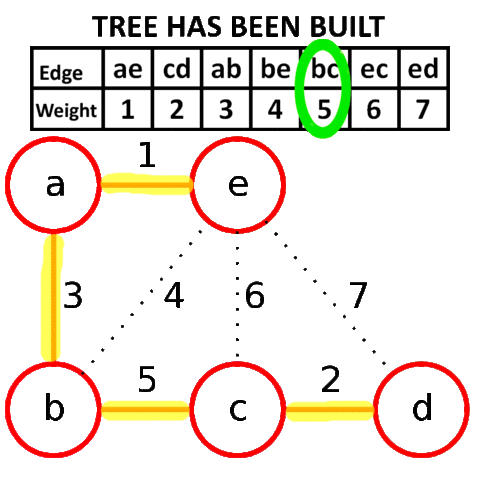
Алгоритм Крускала достаточно прост в своей идее и реализации. Он заключается в сортировке всех рёбер в порядке возрастания длины, и поочерёдному добавлению их в минимальный остов, если они соединяют различные компоненты связности.

Более формально: пусть мы уже нашли некоторые рёбра, входящие в минимальный остов. Утверждается, что среди всех рёбер, соединяющих различные компоненты связности, в минимальный остов будет входить ребро с минимальной длиной.

Для реализации алгоритма Крускала необходимо уметь сортировать рёбра по возрастанию длины (для этого воспользуемся собственным типом данных) и проверять, соединяет ли ребро две различных компоненты связности. Для этого будем просто поддерживать текущие компоненты связности с помощью структуры данных DSU.

Визуализация работы алгоритма Крускала:

Реализация алгоритма Крускала

Используем реализацию DSU со всеми оптимизациями из соответствующей лекции:

Различия в скорости работы

На практике чаще используется алгоритм Крускала.

brestprog

Олимпиадное программирование в Бресте и Беларуси

Источник

Сколько деревьев в графе

Графы и их остовные деревья

Рассмотрим план шести ежедневных рейсов некоторой авиакомпании между некоторыми парами из аэропортов a, b, c и d, показанный на рисунке 1. Для формализации такой и многих других ситуаций в математике используется понятие граф.

Граф — это конечный и не пустой набор вершин и конечный набор ребер, каждое из которых соединяет пару вершин. В нашем примере вершина графа — это аэропорт, а ребро — это рейс авиакомпании. Пара вершин графа может быть соединена несколькими ребрами (это может означать, что авиакомпания совершает несколько рейсов в день). Также ребро может соединять вершину с самой собой; в этом случае оно называется петлей (про такое ребро можно думать, как про прогулочный рейс авиакомпании).

Иначе говоря, с математической точки зрения, на рисунке 1 мы видим граф с четырьмя вершинами a, b, c и d, шестью ребрами, из них одно ребро — петля при вершине c и пара ребер соединяет b с d. Число ребер, исходящих из данной вершины, называется ее степенью, при этом петли считаются дважды; степени вершин a, b, c и d — 1, 4, 4 и 3 соответственно.

Изображенный граф является связным, т.е. из любой его вершины можно пройти в любую другую, пройдя по нескольким его ребрам.

Предположим, нам требуется сократить число ребер связного графа, сохранив его связность. Нетрудно видеть, что это можно сделать тогда и только тогда, когда граф содержит цикл.

Цикл — это маршрут, составленный из различных ребер, обходящий несколько вершин без повторений и возвращающийся в исходную вершину. Число ребер в цикле называется длиной цикла. Например, в нашем графе есть два цикла длины три с вершинами b, c и d, один цикл длины два с вершинами b и d, а также петля при вершине c образует цикл длины один.

Действительно, если из любого цикла связного графа выбросить любое ребро, то граф останется связным. Более того, если после удаления некоторого ребра граф остался связным, то это ребро принадлежало некоторому циклу — этот цикл образован самим ребром и кратчайшим путем между его концами в оставшемся графе.

Удаление ребра из цикла можно повторять, пока мы не придем к графу без цикла. Полученный граф называется остовным деревом исходного графа.

Вообще говоря, связный граф без циклов называется деревом. В таких графах нет петель и из любой их вершины в любую другую есть единственный путь по ребрам без повторений вершин.

На рисунке 2 вы видите все пять различных остовных деревьев нашего исходного графа.

Число остовных деревьев в данном графе Γ мы будем обозначать τ(Γ). Например, если Γ — это граф, рассмотренный выше, то τ(Γ) = 5.

Чтобы проверить понимание данных определений, мы советуем решить следующие два стандартных упражнения про деревья.

1. Докажите, что если дерево имеет хотя бы две вершины, то в нем найдется вершина степени 1.

2. Докажите, что число ребер в любом дереве на единицу меньше числа его вершин. Воспользуйтесь индукцией по числу вершин и предыдущим упражнением.

В частности, из упражнения 2 следует, что независимо от выбора ребер число удаленных ребер в процедуре получения остовного дерева из графа, описанной выше, — одно и то же. (Для связного графа Γ это число называют его первым числом Бэтти; оно обычно обозначается β₁(Γ).)

Ребро связного графа называется мостом, если удаление этого ребра из графа делает граф несвязным; такой граф разбивается на два связных графа, называемые его островами (рис. 3).

Упражнение 3. Пусть граф Γ содержит мост между островами Δ₁ и Δ₂. Докажите, что τ(Γ) = τ(Δ₁) · τ(Δ₂).

Удаление-плюс-стягивание

Пусть ρ есть ребро в графе Γ. Обозначим через Γ\ρ граф, полученный из Γ удалением ребра ρ, и через Γ/ρ — граф, полученный из Γ стягиванием ребра ρ в точку (рис. 4).

Если ребро ρ не является петлей, тогда выполняется следующее соотношение:

которое мы будем называть удаление-плюс-стягивание.

Действительно, остовные деревья в Γ можно разделить на две категории — те, что содержат ребро ρ, и те, что его не содержат. Для деревьев из первой категории стягивание ребра ρ в точку дает остовное дерево в Γ/ρ, а деревья второй категории являются также остовными деревьями в графе Γ\ρ. Более того, оба этих соответствия взаимно однозначны. Отсюда вытекает формула (*).

Например, если Γ — это первый пример и ρ есть ребро между вершинами b и c, тогда первые два остовных дерева на рисунке 2 соответствуют дереву в Γ\ρ, а последние два соответствуют дереву в Γ/ρ.

Формулу (*) удобно записывать схематически, как показано на рисунке 4. На графе Γ ребро ρ, для которого применяется формула, перечеркнуто.

Заметим, что никакое остовное дерево не содержит петель. Поэтому можно удалить все петли из графа, и число его остовных деревьев останется неизменным. Иначе говоря, для любой петли ρ выполняется равенство

Из формулы удаление-плюс-стягивание можно вывести несколько других полезных соотношений. Например, если в графе Γ есть концевая вершина w (т.е. вершина степени 1), то w и единственное ребро при w можно удалить и в полученном графе Γ\w число его остовных графов не изменится, т.е.

Действительно, обозначим через ρ единственное ребро при w. Заметим, что граф Γ\ρ несвязен, поскольку вершина w не имеет ребер, и, значит, τ(Γ\ρ) = 0. С другой стороны, Γ/ρ = Γ\w, откуда и получаем наше равенство.

На схемах двусторонняя стрелка «↔» будет означать, что соответствующие графы имеют то же число остовных деревьев; например, из выведенных соотношений можно получить следующую диаграмму (рис. 5), означающую, в частности, что τ(Γ) = 2 · τ(Δ).

Равенства, описанные выше, дают алгоритм вычисления τ(Γ). Действительно, для любого ребра ρ оба графа Γ\ρ и Γ/ρ имеют меньшее число ребер. Таким образом, удаление-плюс-стягивание сводит нахождение числа остовных деревьев Γ к нахождению числа остовных деревьев более простых графов.

Деревья в веерах

Графы следующего вида (рис. 6) называются веерами; веер с n + 1 вершиной будет обозначаться Θ_n.

Применив соотношения, полученные в предыдущем разделе, мы можем составить бесконечную схему, показанную на рисунке 7. В дополнение к веерам \( Θ_n \) в схеме участвуют их вариации \( Θ^′_n \), отличающиеся от \( Θ_n \) дополнительным ребром. При возникновении петель или концевых вершин мы их тут же удаляем.

Введем обозначения \( a_n = τ(Θ_n) \) и \( a^′_n = τ(Θ^′_n) \). Из схемы легко вывести два рекуррентных соотношения:

Таким образом, в последовательности чисел \( a_1, a^′_1, a_2, a^′_2, a_3. \) каждое следующее является суммой двух предыдущих.

Напомним, что последовательность чисел Фибоначчи F_n задается тем же соотношением F_n+1 = F_n + F_n−1 с F₁ = F₂ = 1. Она начинается так:

Далее заметим, что \( Θ_1 \) — это две вершины, соединенные единственным ребром, а \( Θ^′_1 \) — это две вершины, соединенные двойным ребром. Отсюда \( a_1 = 1 = F_2 \) и \( a^′_1 = 2 = F_3 \), а значит,

Можно также вывести рекуррентное соотношение на \( a_n \) без использования \( a^′_n \):

Последовательности, для которых выполняется подобное соотношение, называются линейными рекуррентными последовательностями. Для такой последовательности можно найти формулу для ее общего члена. В нашем случае

Этот процесс подробно описан в книжке [4], которую мы рекомендуем читателю. Поскольку \( 0 Рис. 8

5. Пусть b_n обозначает число остовных деревьев в лестнице Λ_n с n ступеньками в последовательности графов следующего типа (рис. 9):

Воспользуйтесь разработанным методом и докажите, что последовательность b_n удовлетворяет соотношению

(Заметим, что b₁ = 1 и b₂ = 4; отсюда можно быстро посчитать первые члены последовательности:

Вам потребуются еще пара последовательностей графов \( Λ^′_n \) и \( Λ^″_n \), показанных на рисунке 10.

Продвинутое упражнение 6. Колесами называются графы Φ_n следующего типа (рис. 11):

Докажите, что последовательность c_n = τ(Φ_n) удовлетворяет такой рекуррентной формуле:

Замечание. Проще вывести соотношение

Зная, что c₁ = 1, c₂ = 5, последнее равенство позволяет получить выражение для c_n:

здесь L_n = F_n−1 + F_n+1 ; эта последовательность называется числами Люка. Как и числа Фибоначчи, числа Люка часто появляются в различных комбинаторных задачах.

Заключительные замечания

Подсчет числа остовных деревьев связан с расчетом электрических цепей. Предположим, граф Γ описывает электрическую цепь, в которой каждое ребро — это сопротивление в один ом, источник питания подключен к вершинам a и b и I есть общий ток в цепи, измеренный в амперах. Нам надо посчитать ток через одно из сопротивлений.

Пусть ρ есть ребро Γ с выбранным направлением. Заметим, что все остовные деревья Γ можно разделить на три типа: (1) те, в которых на пути из a в b ребро ρ появляется с положительной ориентацией; (2) те, в которых на пути из a в b ребро ρ появляется с отрицательной ориентацией; (3) те, в которых на пути из a в b ребро ρ не появляется. Обозначим через τ₊, τ₋ и τ₀ число деревьев в этих трех категориях. Очевидно, что τ(Γ) = τ₊ + τ₋ + τ₀.

Силу тока I_ρ вдоль ρ можно вычислить по следующей формуле:

Доказательство получается прямой проверкой правил Кирхгофа для значений токов, полученных по этой формуле, для всех ребер в Γ.

Есть множество других примеров использования правил Кирхгофа в теории графов. Например, в [7] они используются в физическом доказательстве формулы Эйлера

где В, Р и Г обозначают число вершин, ребер и граней многогранника соответственно.

Формула удаление-плюс-стягивание применялась при решении так называемой задачи о квадрировании квадрата. История этой задачи и ее замечательное решение обсуждаются в книжках [6] и [2]; идея этого решения также основана на оригинальном использовании электрических цепей.

Приведенный нами вывод рекуррентных формул для чисел остовных деревьев в веерах, лестницах и колесах дается в [8]; эта задача также обсуждается в классической книжке [3].

где Π_n обозначает полный граф с n вершинами (рис. 12).

Равенство (**) называется формулой Кэли. Наиболее известным доказательством является так называемый код Прюфера — способ однозначного кодирования дерева упорядоченной последовательностью из его вершин; нескольким другим доказательствам посвящена глава 30 в [1]. В расширенной версии настоящей статьи [5] приводится доказательство, основанное на формуле удаление-плюс-стягивание.

Для числа раскрасок вершин графа выполняется аналогичная формула: удаление-минус-стягивание. А именно, пусть χ(Γ, k) обозначает число раскрасок графа Γ в k цветов, при которых концы каждого ребра покрашены в разные цвета. Тогда выполняется соотношение

Действительно, допустимые раскраски графа Γ\ρ можно разбить на две категории: (1) те, в которых концы ребра ρ покрашены в разные цвета, такие остаются допустимыми в графе Γ; (2) те, в которых концы ребра ρ покрашены в один цвет, каждой такой раскраске соответствует единственная раскраска Γ/ρ. Отсюда — формула.

Упражнение 7. Докажите что для любого графа Γ функция χ(Γ, k) является многочленом с целыми коэффициентами от k; он называется хроматическим многочленом графа Γ.

Подсказка. Воспользуйтесь индукцией по общему числу ребер и вершин графа и формулой удаление-минус-стягивание.

Источник