Что такое пересечение фигур

Презентация к уроку

Цели:

Литература: Учебник Л.Г. Петерсон «Математика» 2 (1-4) с.76-77, мет. пособия: Л.Г. Петерсон «Математика во 2 классе» с. 87-88.

Оборудование: Компьютер, интерактивная доска, мультимедийный проектор, карточки с индивидуальными заданиями, инвентарь для фокусов, краски.

По типу урок введения нового знания.

Применяются фронтальная, индивидуальная, самостоятельная формы организации познавательной деятельности учащихся:

Форму урока составляют традиционные структурные компоненты.

Организационный момент имеет мобилизующий характер, реализуется в стихотворной форме. Он же обозначает в уроке сюжетную линию.

Устный счет включал в себя разноплановые задания:

Работа с геометрическим материалом реализуется в виде индивидуальной самостоятельной формы работы.

Отработка вычислительных навыков проходит в форме самостоятельной работы одновременно на индивидуальных карточках и у доски. Поэтапное нажатие правильных ответов на интерактивной доске приводит к раскрашиванию изображенной лошадки.

Данный тип урока предполагает закрепление умения решать задачу на сравнение.

Электронные физкультминутки были специально разработаны для данного урока и использованы с целью здоровьесбережения учащихся, раскрепощения.

Включение фокусов, подводящих к выполнению определенного задания не только помогают поддержать сюжетную линию, но и позволяют включить в урок сведения, способствовавшие познавательной активности детей, развитию кругозора, снятию эмоционального напряжения.

Интеграцией в данный урок является цветовая диагностика с использованием техники фотокопии. Это позволяет детям выразить чувства на символическом уровне и выявить благоприятное воздействие происходящих на уроке событий. Ведь восприятие цвета меняется в зависимости от состояния и настроения.

Ход урока

I. Организационный момент.

Мы в цирк идём,
Займём места
Согласно вашему билету.
Нам интересно будет здесь,
Ведь здесь чудес у нас не счесть
И вы увидите все это!

II. Этап положительного самоопределения в учебной деятельности.

Упомянуть о клоуне Фоке (стих приветствие, проверка готовности, настрой на урок)

Вот первый гость,
Он клоун – Фока.
Умеет всё,
Он в деле дока.
И настроенье у него – Во… (показать…)
Всегда отличное.
А у вас какое?

(Цветовая диагностика настроения)

– У кого сегодня хорошее настроение? Раскрасьте карандашом бантик у клоуна Фоки в зеленый цвет, если настроение хорошее, в синий – если не очень хорошее, в красный – если плохое.

– Постараемся с хорошим настроением поработать на уроке.

Устный счёт:

– Ребята, мы с Фокой приглашаем сюда счастливого обладателя билета под номером 420! (выходит ребёнок) За смелость примите конфету!

– Нам нужны ещё смельчаки.

– Назовите предыдущее от 420 число (419).

– Назовите число, следующее за 699 (700).

– Назовите число, состоящее из 4 сотен, 5 единиц. (405).

– Назовите число, состоящее из 3 сотен, 4 десятков, 2 единиц (342).

– Какое число увеличили на 117 и получили 247 (130).

– Какое число в этом примере является самым маленьким (832-30+25=827)? (25).

– Какое в этом примере самое большое однозначное число (16-6-2=8)? (8).

– Обладатели билетов с номерами 2 и 366.

– Какой цирк без ФОКУСОВ?

Цирк без фокусов не цирк –
Это знает каждый.
Если скажем: «Але-апп!»
И перевернём вдруг карты,
То получим слово мы.
Ну, готовы, раз, два, три. (Але-апп!)

– Получилось слово? (Слово – ПЕРЕСЕЧЕНИЕ) (Слайд)

– Как вы понимаете слово пересечение?

– Кто догадался, какая тема сегодняшнего урока?

Тема нашего урока «Пересечение геометрических фигур»

Фокус с ниткой.
Фока, что это такое
У тебя на пиджаке?
Убери скорее нитку,
Спрячь её своей руке.

Бесконечная нитка

Фокусник замечает у себя на пиджаке, около лацкана, белую нитку, несколько раз пытается смахнуть ее. Но нитка не «смахивается». Фокусник берет ее конец и тянет вниз. Нитка начинает вытягиваться из пиджака. Чем больше она вытягивается, тем больше удивляется фокусник. А длина нитки — несколько десятков метров! Механика фокуса: белая нитка с катушки наматывается на короткий цветной карандаш (столько, сколько намотается), кладется в боковой внутренний карман и ее хвостик (1—2 см) протаскивается иголкой сквозь ткань пиджака наружу. Карандаш нужен для того, чтобы в кармане «не осталось следов», если кто-то из зрителей попросит фокусника показать карман; карандаш — не катушка, он не поможет разгадке этого фокуса.

– На какую геометрическую фигуру похожа эта ниточка? (прямая, отрезок, луч) (Интернет-ресурс)

III. «Открытие» учащимися новых знаний.

1. Посмотрите на этот рисунок.

Кот в путь отправиться готов,
Но как ему пройти?
Ведь параллельные
Натянуты пути.

Что вы здесь видите? (геометрические фигуры)

– Назовите их. (точка, прямые параллельные и пересекающиеся,)

– Какие прямые на рисунке можно назвать параллельными?

– Какие могут пересекаться?

– Они могут пересекаться только в одной точке?

– Где в жизни мы можем встретить пересекающиеся прямые?(рамы на окне)

– А параллельные прямые?(рельсы, высоковольтные линии)

2. Работа на индивидуальных листочках.

Чтобы найти точки пересечения прямых, лучей и отрезков, нужно:

– Начертить параллельные линии и пересекающиеся.

– Проверьте друг у друга правильность выполнения задания.

IV. Физминутка двигательная

V. Самостоятельная работа с проверкой

Математический фокус с карандашами

Факир, волшебник он и маг
Всё отгадать ему пустяк.
Он вам карандаши припас.
А сколько? Ты узнай сейчас.

Из коробки уберите часть карандашей. Предложите желающему из зрителей задумать любое число из второго десятка. Цифры этого числа пусть сложит между собой. Когда вам назовут результат, такое количество карандашей верните обратно в коробку.

Если теперь зритель пересчитает в коробке все карандаши, то их количество будет равно задуманному числу.

Секрет фокуса: В коробке нужно оставить девять карандашей — остальные убирать. Какое бы число ни задумали зрители, сумма его цифр (если к ней прибавить 9) будет равна задуманному числу. Например: задумали число 17. 1 + 7 = 8. Восемь карандашей верните обратно в коробку. 9 + 8 = 17.(Интернет-ресурс)

– Внимание, на арене нашего цирка благороднейшая маркиза по имени Алиса!

Вот лошадка без попоны,
Но скакать она готова.
Только помогите ей
И раскрасьте поскорей.

При нажатии правильного ответа закрашивается определенная часть лошадки.

VI. Физминутка для глаз.

VII. Закрепление изученного материала.

– У нас в цирке есть ещё одна незаменимая артистка! И вы не поверите, это тоже крупнокопытное млекопитающее животное!

Выгоняли рога
Погулять на луга.
И рога вечерком
Прибрели с молочком.
(Ответ: Корова) (Слайд)

– Ребята, кто первым найдёт в учебнике задание о наших артистках, тому – приз! (задача № 8) (Слайд с этими животными)

VIII. Д/з.

IХ. Подведение итогов урока.

(стих)

– Вот и окончено наше представление!

– Чему учились? Что вы нового узнали?

– Вам понравилось? И клоун Фока очень доволен вашими успехами!

Спасибо, Фока говорит.
Вас всех, ребята, хвалит
И на прощанье вам всем
Он свой портрет подарит.

Фока дарит вам свой портрет. Переверните карточки. Видите его счастливую мордочку? Нет? И не удивительно! Как же в цирке без фокусов? Этот фокус вы сделаете сами. Для того чтобы увидеть изображение Фоки, вы должны ярко закрасить лист цветом своего настроения. (Сквозь краску проявляется восковое изображение).

Источник

Основные геометрические фигуры

Содержание:

Общие представления о геометрических фигурах. Объединение и пересечение фигур

На рисунках 2.1 и 2.2 изображены различные геометрические фигуры. Всякую геометрическую фигуру мы представляем себе составленной из точек.

Часть любой геометрической фигуры ТЭ.КЖ6 ЯВ-ляется геометрической фигурой.

Определение. Любое множество точек называют геометрической фигурой.

На рисунке 2.3 отрезок АВ есть часть прямой а, на рисунке 2.4 круг есть часть круга , на рисунке 2.5 шар вписан в куб и является частью куба.

Объединение нескольких фигур есть геометрическая фигура. На рисунке 2.6 фигура состоит из трех кругов, на рисунке 2.7 фигура состоит из треугольника и квадратов, на рисунке 2.8 фигура составлена из двух тетраэдров, на рисунке 2.9 фигура состоит из нескольких кубов. Объединение обозначается знаком .

Пересечение геометрических фигур есть также геометрическая фигура. На рисунке 2.10 отрезки АВ и CD пересекаются в точке Р. На рисунке 2.11 также отрезки MP и РК пересекаются в точке Р. Пересечением же отрезков ЕН и КХ на рисунке 2.12 является отрезок НК. Пересечение обозначается знаком .

Пример:

Рассмотрите возможные случаи взаимного расположения двух треугольников. В каждом случае назовите их пересечение.

Решение:

На рисунках 2.13—2.19 показано, что пересечение двух треугольников может:

а) не содержать точек (рис. 2.13);

б) состоять из одной точки (рис. 2.14);

в) быть отрезком (рис. 2.15);

г) быть треугольником (рис. 2.16);

д) быть четырехугольником (рис. 2.17);

е) быть пятиугольником (рис. 2.18);

ж) быть шестиугольником (рис. 2.19).

На рисунках 2.13—2.19 изображены различные случаи пересечения треугольников, если они лежат в одной плоскости. Однако, если треугольники лежат в разных плоскостях, то пересечением может быть:

б) отрезок (рис. 2.21, 2.22);

в) пустое множество точек (рис. 2.23).

Изображение геометрических фигур

Изображение плоских фигур на листе бумаги (или на доске) подчинено некоторым правилам и выполняется с использованием различных инструментов: линейки, угольника, транспортира, циркуля.

При изображении или построении плоских фигур мы не меняем формы и размеры тех фигур, которые изображаем. При этом сохраняются длины отрезков, величины углов, параллельность прямых и т. д. В геометрии говорят, что при этом получаются равные фигуры. Если нужно изобразить очень большие или очень маленькие фигуры, то сохраняются формы, а размеры могут быть изменены (в одном и том же отношении). При этом получают так называемые подобные фигуры.

Изображать пространственные фигуры на плоскости (листе бумаги) намного сложнее.

Наиболее важные из правил изображения пространственных фигур:

— все линии, которые не видны, которые закрыты гранями (плоскостями), изображаются пунктирными линиями;

— плоскости на рисунках изображаются иногда параллелограммами (рис. 2.24), а чаще — произвольной областью (рис. 2.25);

— длины отрезков сохраняются не всегда, но всегда середины отрезков изображаются серединами их изображения (это свойство означает, что если на модели у нас отмечена середина ребра, то и на рисунке будет обозначена тоже середина ребра);

— параллельные прямые (отрезки), имеющиеся на реальной модели, на рисунках тоже изображаются параллельными прямыми (отрезками).

Точки и прямые

Точки могут произвольно располагаться в пространстве: лежать и не лежать на плоскости (на рис. 2.26 точки А и Б лежат на плоскости, а точка С не лежит), принадлежать различным фигурам и не принадлежать им (на рис. 2.27 точка А принадлежит шару, а на рис. 2.28 не принадлежит ему).

Пусть даны две точки А и В. Проведем через точки А л В прямую (рис. 2.29). У нас появляется еще одно, важное понятие геометрии — прямая, которая также состоит из точек.

Изобразить прямую целиком невозможно, мы лишь условно изображаем ее часть (рис. 2.29).

Некоторые важные проблемы в геометрии решают путем введения законов — аксиом, которые принимаются без доказательства.

Слово «аксиома» в переводе с греческого языка означает «бесспорная истина, не требующая доказательств», т. е. очевидный факт, ясный сам по себе.

Аксиома 1.

Через любые две точки можно провести прямую, и только одну.

Прямые обозначаются строчными латинскими буквами: и т. д., а также соответствующими точками, лежащими на ней. Например, прямую на рисунке 2.29 можно обозначить АВ.

Взаимное расположение точек и прямых

Точки и прямые могут по-разному располагаться по отношению друг к другу (рис. 2.30).

Про точки М и К говорят, что они лежат на прямой , или что точки М и К принадлежат прямой . Точки А и В не лежат на прямой или не принадлежат прямой а.

Про прямую иногда говорят, что она проходит через точки. Так, прямая на рисунке 2.30 проходит через точки М, К. Можно также сказать, что прямая не проходит через точку А.

В курсе геометрии применяются некоторые удобные знаки, которые относятся к так называемой теории множеств: знак принадлежности и знак непринадлежности .

Запись читается: точка С принадлежит прямой р. Глядя на рисунок 2.30, можно записать:

Запись читается: точка D не принадлежит прямой р. Глядя на рисунок 2.30 можно записать:

Плоскости

Плоскости расположены в пространстве, в пространстве есть бесконечно много различных плоскостей. На рисунке 2.31 изображены несколько плоскостей, пересекающихся по одной прямой, а на рисунке 2.32 — параллельные друг другу плоскости.

На рисунке 2.33 изображены плоскость , прямые и точки А, В и С. Про точку А и прямую говорят, что они лежат в плоскости или принадлежат ей. Про точки Б и С и прямую говорят, что они не лежат в плоскости или не принадлежат ей.

Принадлежность прямой плоскости обозначают знаком — включение, который показывает, что некоторое множество точек принадлежит другому множеству точек, например:

— точка А принадлежит плоскости ; — точка Б не лежит в плоскости ;

— прямая принадлежит плоскости ; — прямая не принадлежит плоскости .

Одно из свойств взаимного расположения прямой и плоскости формулируется как аксиома — аксиома прямой и плоскости.

Аксиома 2.

Прямая, проходящая через две точки плоскости, принадлежит этой плоскости. (Аксиома прямой и плоскости.)

Аксиома 3.

Через три точки, не лежащие на одной прямой, проходит одна и только одна плоскость. (Аксиома плоскости.)

Теорема 1. Через прямую и не лежащую на ней точку проходит одна, и только одна плоскость.

Любая прямая разбивает плоскость на два непустых множества (рис. 2.34). Объединение прямой с одним из образовавшихся множеств называется полуплоскостью. Прямую называют границей полуплоскости. На рисунке 2.34 прямая одновременно является границей обеих полуплоскостей.

Плоскость разбивает пространство на два множества, которые на рисунке 2.35 заштрихованы. Объединение этой плоскости с одним из образовавшихся множеств и называется полупространством. Плоскость называется границей полупространства. Из рисунка 2.35 ясно, что плоскость определяет сразу два полупространства.

Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:

Смотрите также дополнительные лекции по предмету «Математика»:

Источник

Пересечение поверхностей и способы построения линий пресечения

Пересечение поверхностей и способы построения линий пресечения

Линия пересечения принадлежит обеим пересекающимся поверхностям и образуется множеством их общих точек. Следовательно, построение линии пересечения поверхностей сводится к построению этих общих точек.

При пересечении поверхностей вращения порядок линии пересечения определяется умножением порядков пересекающихся поверхностей. Например, если пересекаются круговой конус (поверхность 2-го порядка) и сфера (поверхность 2-го порядка), то линия пересечения является кривой 4-го порядка.

Определение способа построения линии пересечения зависит от взаимного расположения пересекающихся поверхностей, а также от их расположения относительно плоскостей проекций.

вариантов пересечения поверхностей геометрических тел в зависимости от их взаимного расположения можно выделить четыре случая, которые позволяют определить и представить форму линии пересечения поверхностей:

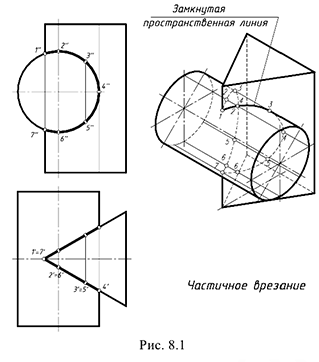
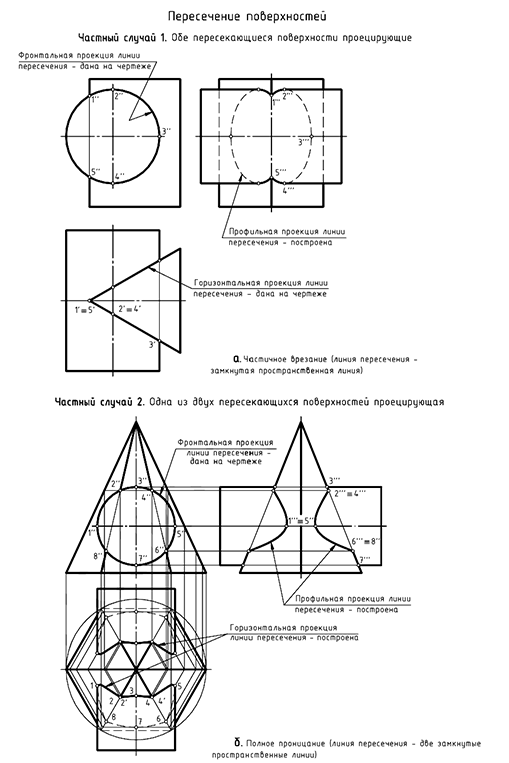
I случай. Частичное врезание (рис. 8.1). В этом случае линией пересечения является одна замкнутая пространственная линия.

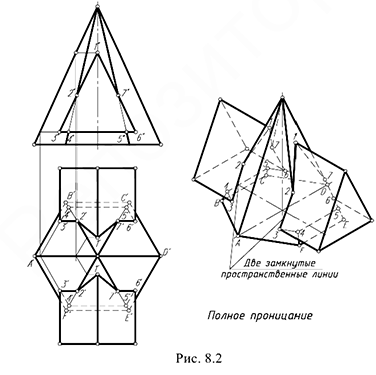
II случай. Полное проницание (рис. 8.2). В этом случае линией пересечения являются две замкнутые пространственные линии.

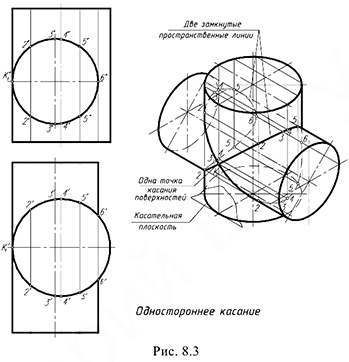
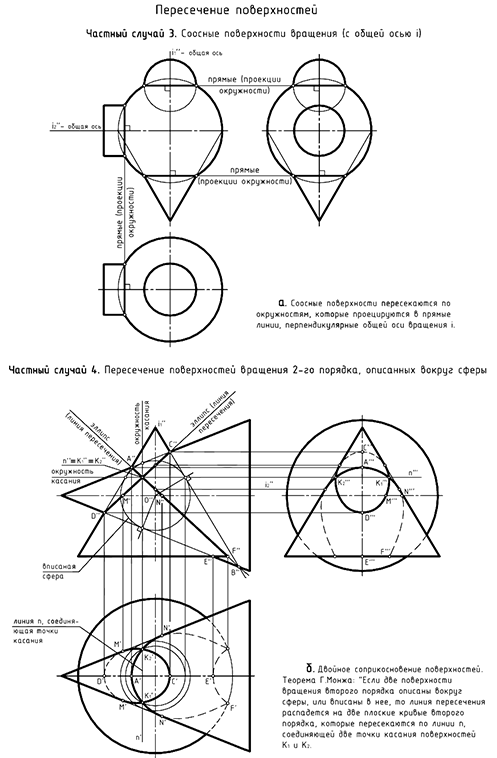
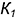
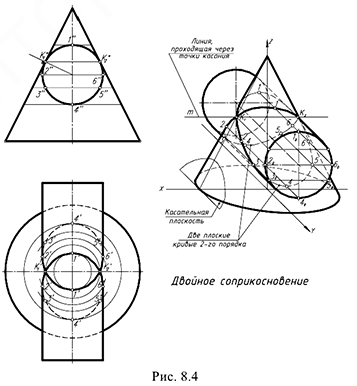
III случай. Одностороннее соприкосновение (рис. 8.3). В этом случае поверхности соприкасаются в одной общей точке и линия их пересечения, проходя через эту точку, распадается на две замкнутые пространственные линии (поверхности имеют одну общую касательную плоскость).

IV случай. Двойное соприкосновение (рис. 8.4).

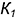
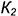
В этом случае поверхности имеют две точки соприкосновения и и линия их пересечения распадается на две плоские кривые в соответствии с теоремой 2 (С. А. Фролов «начертательная геометрия»):

«Если две поверхности вращения второго порядка имеют касание в двух точках, то линия их пересечения распадается на две кривые второго порядка, плоскости которых проходят через прямую /77, соединяющую точки касания» (поверхности имеют две общие касательные плоскости).

В зависимости от расположения пересекающихся геометрических тел относительно плоскостей проекции и участия в пересечении геометрических тел, имеющих проецирующую поверхность (как призма или цилиндр) или не имеющих проецирующей поверхности (пирамида, конус, шар, тор, тороид, наклонная призма или наклонный цилиндр, глобоид и др.), следует выбрать оптимальный способ построения проекций линии пересечения поверхностей на чертеже.

По этим признакам способы построения линий пересечения поверхностей можно объединить в две группы:

Первая группа: частные случаи пересечения поверхностей, когда для построения линий пересечения не требуется применения специальных способов, а используется частное положение пересекающихся геометрических тел относительно плоскостей проекций.

Вторая группа: общие случаи пересечения поверхностей, когда для построения линий пересечения требуется применить специальные способы посредников.

Частные случаи пересечения поверхностей

К первой группе частных случаев пересечения поверхностей относятся следующих четыре случая:

1 случай: пересечение геометрических тел, боковые поверхности которых являются проецирующими, то есть, перпендикулярны какой-либо плоскости проекций.

2 случай: пересечение геометрических тел, у одного из которых боковая поверхность является проецирующей.

3 случай: пересечение соосных поверхностей вращения, т. е. имеющих общую ось вращения,

4 случай: пересечение поверхностей вращения второго порядка, описанных вокруг сферы (по теореме Г. Монжа).

Рассмотрим на примерах построение проекций линий пересечения поверхностей геометрических тел в четырех частных случаях первой группы.

Следует отметить, что перечисленные частные случаи пересечения поверхностей наиболее часто встречаются при формообразовании различных реальных деталей.

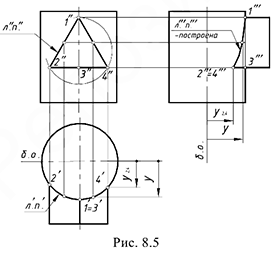
1-й частный случай. На рис. 8.5 показан пример построения проекций линии пересечения поверхностей горизонтально-проецирующего цилиндра и фронтально-проецирующей прямой правильной треугольной призмы, то есть пересекаются два геометрических тела, боковые поверхности которых занимают относительно плоскостей проекций проецирующее положение.

Характерный признак 1-го частного случая: на заданных проекциях тел определяются две проекции искомой линии пересечения:

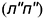
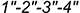
-фронтальная проекция линии пересечения совпадает с вырожденной в ломаную линию боковой поверхностью призмы;

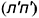
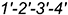
-горизонтальная проекция линии пересечения совпадает с участком окружности, которая является вырожденной проекцией боковой поверхности цилиндра.

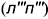
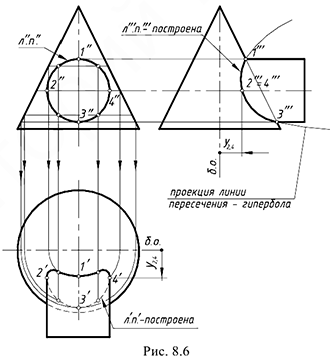
Следовательно, требуется достроить только профильную проекцию линии пересечения, построив профильные проекции обозначенных точек по их принадлежности одному из тел (в данной задаче — цилиндру), и соединить их плавной кривой с учетом ее видимости на поверхностях. 2-й частный случай.

На рис. 8.6 показан пример построения проекций линии пересечения поверхностей прямого кругового конуса и фронтально-проецирующего цилиндра, то есть пересекающихся геометрических тел, у одного из которых боковая поверхность проецирующая.

Характерный признак 2-го частного случая: на заданных проекциях тел определяется одна проекция линии пересечения:

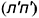
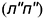
Следовательно, требуется достроить горизонтальную и профильную проекции линии пересечения, построив горизонтальные и профильные проекции обозначенных точек по их принадлежности конусу, и соединить построенные на проекциях точки плавными кривыми линиями с учетом их видимости на поверхностях.

. На профильную проекцию предмета пространственная кривая линия пересечения 4-го порядка проецируется в виде участка гиперболы.

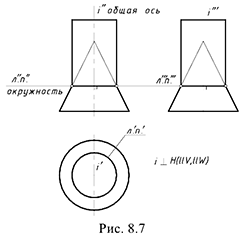
Пересечение соосных геометрических тел

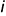
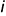
Соосными называются геометрические тела вращения, имеющие общую ось вращения «». Поверхности соосных тел пересекаются по окружностям, перпендикулярным их общей оси. Если общая ось «» соосных геометрических тел является прямой проецирующей (т. е. она перпендикулярна какой-либо одной плоскости проекций, а двум другим параллельна), то окружность пересечения проецируется дважды в прямую линию, перпендикулярную их общей оси, на те плоскости проекций, которым эта общая ось параллельна.

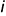
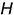
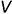
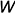
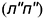
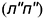
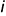
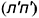
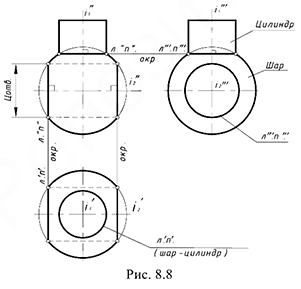
На рис. 8.7 показан пример построения линии пересечения соосных геометрических тел — конуса и горизонтально-проецирующего цилиндра, имеющих общую горизонтально-проецирующую ось (ось перпендикулярна и параллельна и ). Линией пересечения является окружность, фронтальная и профильная проекции которой представляют собой прямые линии, перпендикулярные их общей оси и проходящие через точки пересечения фронтальных и профильных очерков поверхностей. Горизонтальная проекция этой окружности пересечения совпадает с вырожденной горизонтальной проекцией боковой поверхности цилиндра.

На рис. 8.8 показан пример цилиндр построения линий пересечения двух пар соосных поверхностей:

Пересечение поверхностей вращения второго порядка, описанных вокруг сферы (по теореме Г. Монжа).

Напоминаем, к поверхностям вращения второго порядка относятся круговые цилиндр и конус, шар, эллипсоиды, параболоид и одно-, двуполостные гиперболоиды.

Эллиптические цилиндры и конусы, а также наклонный круговой конус — это не поверхности вращения!

Все торы (открытый, закрытый и самопересекающийся), глобоиды и тороиды относятся к поверхностям вращения четвертого порядка!

В 4-м частном случае имеет место двойное соприкосновение пересекающихся поверхностей вращения второго порядка, описанных вокруг сферы, и построение линии пересечения основано на теореме 2 (С. А. Фролов «Начертательная геометрия» [23]):

Теорема 3, известная как теорема Г. Монжа, вытекает из теоремы 2: «Если две поверхности вращения второго порядка описаны вокруг третьей поверхности второго порядка или вписаны в нее, то линия их пересечения распадается на две кривые второго порядка, плоскости которых проходят через прямую, соединяющую точки касания».

Практическое применение теоремы возможно в том случае, когда две поверхности вращения второго порядка описаны вокруг сферы или вписаны в нее.

Использовать теорему Г. Монжа для построения на чертеже линии пересечения поверхностей можно при наличии в задаче четырех обязательных графических условий:

При соблюдении этих четырех условий на одной из заданных проекций можно построить проекции двух плоских кривых, на которые распадается искомая линия пересечения:

-точки пересечения очерков поверхностей на этой проекции принадлежат искомой линии пересечения и через эти точки проходят прямые, в которые проецируются плоские кривые пресечения;

. Точки касания (соприкосновения) поверхностей и определяются на пересечении проекций окружностей касания вписанной сферы с каждой из поверхностей.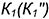

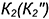
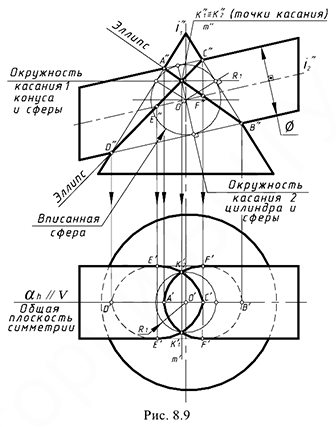
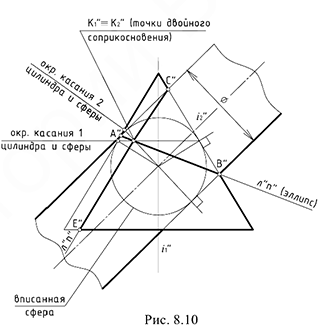
На рис. 8.9 показан пример построения проекций линии пересечения поверхностей вращения второго порядка — прямого кругового конуса и наклонного кругового цилиндра, описанных вокруг общей сферы. Для решения задачи использована теорема Г. Монжа, поскольку здесь соблюдены все четыре обязательных условия ее применения:

Построение проекций линии пересечения поверхностей по теореме Г. Монжа выполняется по следующему графическому алгоритму:

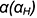
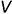
1-е действие. Определить проекцию предмета, на которую плоские кривые проецируются в отрезки прямых линий: в данной задаче это фронтальная проекция, так как общая плоскость симметрии параллельна фронтальной плоскости проекций .

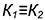
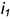
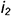
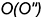
2-е действие. Построить фронтальные совпадающие проекции точек соприкосновения заданных поверхностей, лежащих на пересечении проекций окружностей касания вписанной сферы с каждой из поверхностей (прямые линии — проекций этих окружностей касания — строятся как линии пересечения соосных поверхностей, так как вписанная сфера образует две пары соосных поверхностей — конус/сфера с общей осью и цилиндр/сфера с общей осью . На чертеже проекции этих окружностей касания проходят через точки, полученные на пересечении перпендикуляров, проведенных из точки — центра вписанной сферы — к образующим конуса (окружность касания 1) и цилиндра (окружность касания 2).

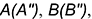
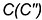
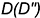
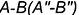
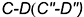
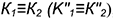
3-е действие. Отметить на фронтальной проекции точки и пересечения очерков поверхностей и построить фронтальные проекции плоских кривых пересечения 2-го порядка, соединив прямыми линиями и противоположные точки пересечения очерков (обе прямые обязательно должны пройти через построенные проекции точек соприкосновения поверхностей ;

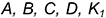
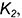
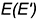
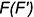
4-е действие. Построить горизонтальные проекции двух плоских кривых пересечения — эллипсов, по горизонтальным проекциях обозначенных точек и построенных по принадлежности поверхности конуса; обозначить и построить точки и , которые лежат на очерковых образующих горизонтальной проекции цилиндра и определяют границу видимости кривых на горизонтальной проекции предмета, а также отметить и построить необходимое количество промежуточных точек (здесь не обозначены).

5-е действие. Оформить фронтальный и горизонтальный очерки пресекающихся поверхностей.

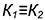
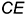
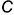
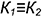
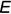
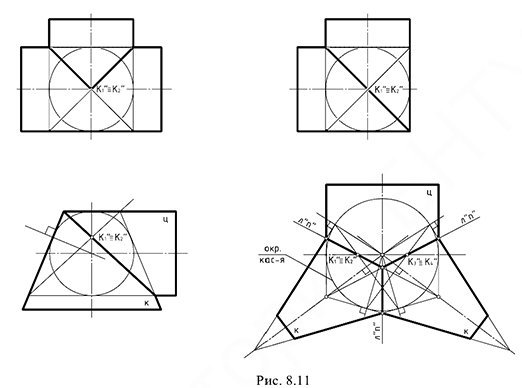
. Построение точек соприкосновения поверхностей особенно важно в задачах, где по условию нельзя определить одну из четырех точек пересечения очерков поверхностей. Совпадающие проекции точек соприкосновения в этом случае определят направление одной из двух прямых линий — проекций плоских кривых пересечения (рис. 8.10). В данном случае проекция плоской кривой линии пересечения проведена через точки и . Точка определяется на основании конуса.

На рис. 8.11 показаны примеры построения линий пересечения поверхностей второго порядка, описанных вокруг сферы, с применением теоремы Г. Монжа. Они часто встречаются при конструировании различных переходов цилиндрических и конических труб, или пересечений отверстий в деталях.

Общие случаи пересечения поверхностей и способы построения линий пересечения поверхностей

Ко второй рассматриваемой группе относятся общие случаи пересечения геометрических тел, боковые поверхности которых могут занимать относительно плоскостей проекций непроецирующее положение (это наклонные призмы и цилиндры), а также геометрические тела, поверхности которых непроецирующие — это конус, сфера, торы, глобоид, эллипсоид, параболоид и гиперболоиды. Сюда же относятся наклонный эллиптический цилиндр, имеющий круговые сечения, и наклонный круговой конус.

предмета, на которой следует начинать решение задачи, и границы введения посредников.

Для построения проекций точек, принадлежащих линии пересечения поверхностей, способом посредников следует применять общий для всех рассматриваемых способов графический алгоритм.

Графический алгоритм I:

1-е действие. Ввести вспомогательную плоскость или поверхность-посредник.

2-е действие. Построить вспомогательные линии пересечения плоскости — или поверхности-посредника с каждой из заданных поверхностей.

3-е действие. Определить точки пересечения построенных вспомогательных линий пересечения — эти точки принадлежат искомой линии пересечения.

Рассмотрим на примерах применение различных способов вспомогательных посредников для построения проекций линий пересечения поверхностей.

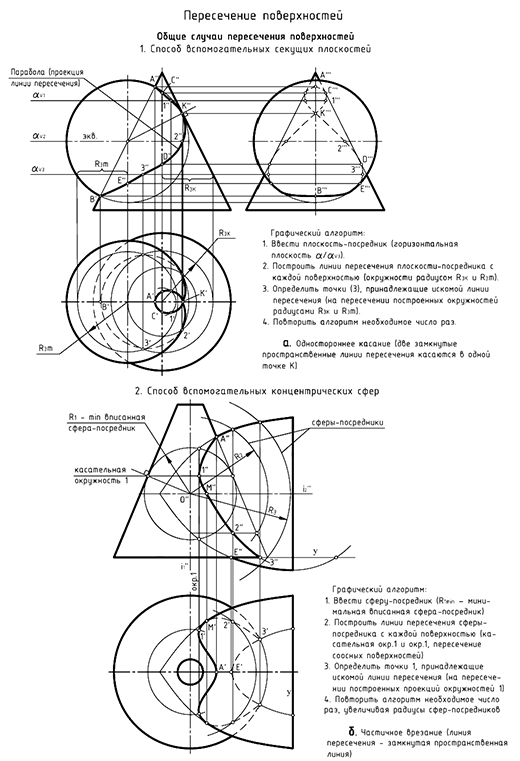
Способ вспомогательных секущих плоскостей уровня

Применение способа вспомогательных секущих плоскостей рационально при наличии д в у х графических условий:

очерков поверхностей принадлежат искомой линии пересечения и определяют верхнюю и нижнюю границу введения плоскостей-посредников на соответствующей проекции предмета.

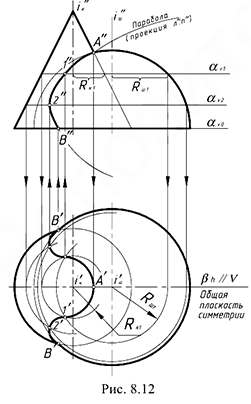
На рис. 8.12 показан пример построения проекций линии пересечения прямого конуса и половины шара.

Для решения задачи требуется предварительно выполнить графический анализ заданных проекций предмета:

А. Выбираем для решения задачи способ вспомогательных секущих плоскостей, так как здесь соблюдены два Рис. 8.12 графических условия его применения:

Б. Решение задачи, то есть введение плоскостей-посредников, начинаем на фронтальной проекции предмета, так как общая плоскость симметрии геометрических тел является фронтальной плоскостью уровня.

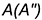
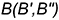
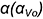
В. Определяем границы введения плоскостей-посредников — это точка пересечения фронтальных очерков и точки пересечения окружностей оснований конуса и полушара, лежащие в горизонтальной плоскости уровня .

Построить проекции точек искомой линии пересечения, выполнив действия предложенного графического алгоритма I:

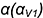
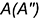
1-е действие. Ввести на фронтальной проекции предмета первую вспомогательную секущую горизонтальную плоскость-посредник произвольно и ниже точки .

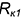
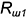
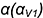
2-е действие. Построить на горизонтальной проекции предмета вспомогательные окружности радиусами и , по которым секущая плоскость-посредник пересекает поверхности конуса и шара.

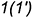
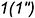
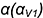
3-е действие. Определить на пересечении построенных вспомогательных окружностей горизонтальные проекции точек , принадлежащих линии пересечения; фронтальные совпадающие проекции этих точек определяются по линии связи на фронтальной проекции плоскости-посредника .

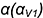
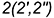
3.1. Повторить действия основного графического алгоритма, введя вторую плоскость-посредник , и построить проекции точек и т. д.

4-е действие. Соединить проекции построенных точек на фронтальной и горизонтальной проекциях предмета плавными кривыми линиями с учетом их видимости на проекциях: на фронтальную проекцию предмета пространственная кривая пересечения проецируется в видимую плоскую кривую второго порядка (участок параболы), поскольку горизонтальная проекция предмета имеет фронтальную симметрию; на горизонтальную проекцию предмета — в участок видимой кривой 4-го порядка сложной формы.

5-е действие. Оформить очерки поверхностей на заданных проекциях предмета с учетом их относительной видимости:

вправо от точек 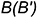(несуществующие части окружностей оснований конуса и шара оставить тонкими линиями).

. Способ вспомогательных секущих плоскостей позволяет строить одновременно две проекции искомой линии пересечения.

Способ вспомогательных концентрических сфер

Основанием для применения сферы в качестве вспомогательной поверх-ности-посредника являются две ее характерные особенности:

Сфера-посредник образует две пары соосных поверхностей с каждой из заданных поверхностей. Каждая образованная пара соосных поверхностей пересекается по соответствующим окружностям, которые проецируются в прямые, перпендикулярные общей оси каждой пары, и проходят через точки пересечения очерков каждой пары соосных поверхностей.

Применение способа вспомогательных концентрических сфер для построения линии пересечения поверхностей возможно при наличии трех следующих графических условий:

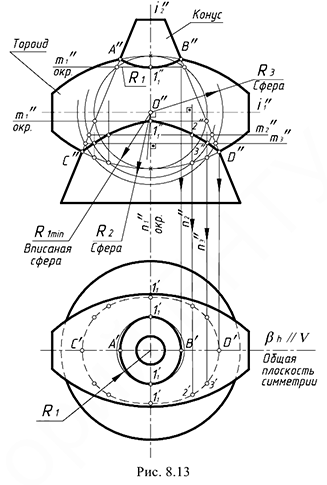
На рис. 8.13 показан пример построения проекций линии пересечения усеченного конуса и тороида (самопересекающийся тор).

Рассмотренный способ вспомогательных секущих плоскостей здесь применять не следует, так как ни одна плоскость уровня не пересекает поверхности одновременно по окружностям (одно из условия применения).

Для решения задачи требуется предварительно выполнить графический анализ заданных проекций предмета.

А. Выбираем для решения задачи способ вспомогательных концентрических сфер, так как здесь соблюдены три графических условия его применения:

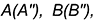
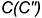
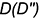
Б. Решение задачи, то есть введение вспомогательных сфер-посредников начинаем на фронтальной проекции предмета, так как общая плоскость симметрии является фронтальной плоскостью уровня и точки и пересечения фронтальных очерков принадлежат линии пересечения.

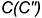
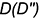
В. Определяем границы введения сфер — это точки и пересечения фронтальных очерков пересекающихся геометрических тел.

Построить проекции точек линии пересечения, выполнив действия предложенного графического алгоритма I.

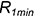
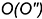
1-е действие. Ввести на фронтальной проекции вспомогательную сферу-посредник минимального радиуса , с центром в точке , вписанную в тороид (минимальная сфера-посредник должна вписываться в одну из поверхностей, а с другой поверхностью — пересекаться).

2-е действие. Построить проекции вспомогательных окружностей пересечения двух пар соосных поверхностей, образованных сферой-посред-ником с каждой заданной поверхностью:

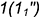
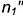
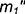
3-е действие. Определить точки пересечения построенных проекций вспомогательных окружностей и , которые принадлежат искомым линиям пересечения (по две пары совпадающих точек).

. Здесь имеет место случай полного проницания (II случай), и линия пересечения распадается на две замкнутые кривые.

Дополнительные действия:

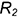
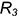
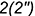
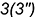
4-е действие. Повторить действия основного графического алгоритма, введя вспомогательные сферы большего радиуса и с тем же центром в точке , и построить следующие пары точек и .

4.1. Достроить горизонтальные проекции построенных точек линии пересечения по принадлежности параллелям конуса.

4.2. Соединить проекции построенных точек на фронтальной и горизонтальной проекциях предмета плавными кривыми линиями с учетом их видимости на проекциях (только линия пересечения 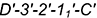будет невидимой на горизонтальной проекции предмета).

5-е действие. Оформить очерки поверхностей на заданных проекциях предмета с учетом их относительной видимости.

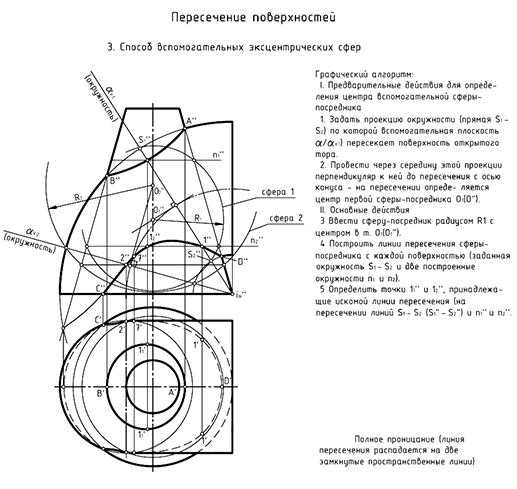
Способ вспомогательных эксцентрических сфер

Наименование способа говорит о том, что вспомогательные сферы имеют разные центры, которые и нужно определять в процессе построения проекций линии пересечения поверхностей.

Способ вспомогательных эксцентрических сфер для построения линии пересечения поверхностей возможно применять при наличии трех следующих графических условий:

Поскольку в этом способе центр каждой вспомогательной сферы нужно определять графическими построениями, первое действие графического алгоритма для построения проекций точек линии пересечения дополняется построением центра каждой вспомогательной сферы.

Порядок графических действий для построения линий пересечения способом вспомогательных эксцентрических сфер показан на двух примерах.

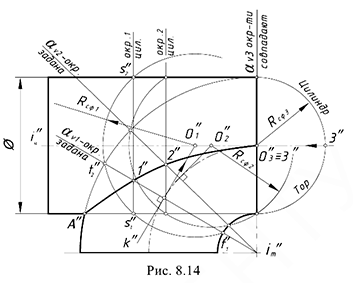
На рис. 8.14 показан пример построения проекции линии пересечения профильно-проецирующего цилиндра с поверхностью четвертой части открытого тора. Задача решается способом вспомогательных эксцентрических сфер, так как здесь соблюдены три необходимых условия для применения этого способа:

Построение проекций точек линии пересечения поверхностей выполняется на заданной фронтальной проекции предмета по предлагаемому графическому алгоритму II.

Графический алгоритм II.

1-е действие. Ввести вспомогательную сферу, выполнив предварительно следующие графические действия.

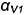
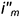
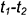
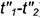
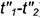
1.1. Задать произвольное круговое сечение поверхности тора фронтально-проецирующей плоскостью , проходящей через его ось ; окружность (ее проекция — прямая линия ) — это заданная линия пересечения тора с искомой вспомогательной сферой, центр которой должен лежать на перпендикуляре к проекции этой окружности — прямой (хорда окружности, в которую проецируется вспомогательная сфера).

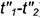
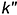
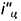
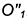
1.2. Провести к прямой через ее середину перпендикуляр и на его пересечении с осью цилиндра определить центр первой вспомогательной сферы — точку .

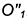
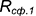
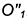
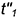
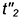
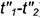
1.3. Провести окружность — проекцию вспомогательной сферы-посредника — с центром в точке , радиус которой определяется расстоянием от точки до одной из крайних точек или прямой .

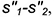
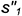
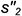
2-е действие. Построить проекцию окружности пересечения построенной сферы-посредника с поверхностью соосного ей цилиндра — это прямая , проходящая через точки и пересечения очерков цилиндра и сферы-посредника.

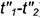
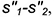
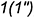
3-е действие. Определить на пересечении построенных проекций заданной окружности и построенной окружности совпадающие точки , принадлежащие искомой линии пересечения заданных поверхностей.

Дополнительные действия:

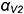
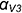
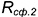
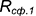
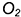
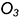
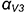
4-е действие. Повторить действия графического алгоритма и построить достаточное количество точек линии пересечения. В данном примере дополнительными сечениями вспомогательных плоскостей и и вспомогательными сферами и с центрами и построены точки 2 и 3, принадлежащие линии пересечения. Причем в плоскости окружности сечений совпадают и совпадающие точки 3 делят существование этих окружностей на две половины — верхняя часть принадлежит цилиндру, а нижняя — тору.

5-е действие. Соединить на фронтальной проекции точки 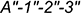линии пересечения плавной видимой кривой.

6-е действие. Оформить очерки поверхностей на заданной проекции.

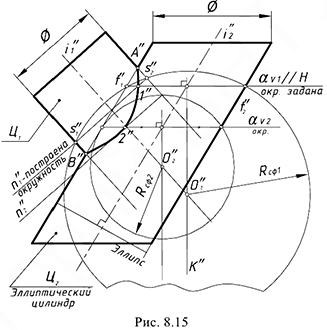
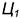
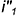
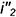
На рис. 8.15 показан пример построения линии пересечения наклонного кругового цилиндра с осью и наклонного эллиптического цилиндра с осью , у которого есть круговые сечения в горизонтальных плоскостях уровня.

Выполнить графический анализ условия и исключить нерациональный способ решения задачи.

Рассмотренный способ вспомогательных секущих плоскостей применять не следует, так как на заданной фронтальной проекции ни одна плоскость уровня не пересекает поверхности одновременно по окружностям или образующим (одно из условий применения).

Рассмотренный способ вспомогательных концентрических сфер применять нельзя, так как проведенные сферы с центром в точке пересечения осей образуют соосные пары только с одной заданной поверхностью 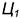(одно из условий применения).

Выбираем для решения задачи способ вспомогательных эксцентрических сфер, так как здесь соблюдены три условия его применения:

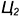
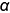
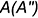
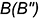
Решение задачи, то есть введение сечений цилиндра (параллельных заданному) горизонтальными плоскостями уровня , начинаем на фронтальной проекции предмета, так как общая плоскость симметрии является фронтальной плоскостью уровня и точки и пересечения фронтальных очерков принадлежат линии пересечения.

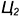
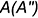
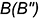
Определяем границы введения сечений цилиндра — это точки и пересечения фронтальных очерков пересекающихся геометрических тел.

Построить проекции точек линии пересечения поверхностей, выполнив действия предложенного графического алгоритма II.

Графический алгоритм II.

1-е действие. Ввести вспомогательную сферу, выполнив предварительные графические действия.

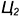
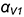
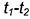
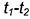
1.1. Задать произвольное круговое сечение эллиптического цилиндра горизонтальной плоскостью — прямую . Эта заданная линия -окружность пересечения эллиптического цилиндра с искомой вспомогательной сферой, центр которой лежит на перпендикуляре, проведенном из середины этой прямой.

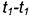
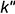
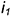
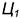
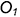
1.2. Провести к прямой через ее середину перпендикуляр и на пересечении с осью кругового цилиндра определить точку — центр первой вспомогательной сферы-посредника.

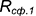
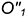
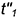
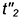
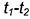
1.3. Провести окружность сферы-посредника радиусом , который определяется расстоянием от точки до одной из точек или прямой .

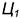
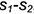
2-е действие. Построить проекцию окружности пересечения сферы-посредника с соосной ей поверхностью кругового цилиндра — это прямая , проходящая через точки пересечения очерков сферы и цилиндра.

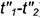
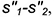
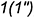
3-е действие. Определить на пересечении заданной окружности и построенной окружности совпадающие точки , принадлежащие искомой линии пересечения.

4-е действие. Повторить действия графического алгоритма II и построить проекции точек ;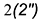

5-е действие. Соединить на фронтальной проекции точки 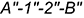линии пересечения плавной видимой кривой.

6-е действие. Оформить очерки поверхностей на заданной проекции.

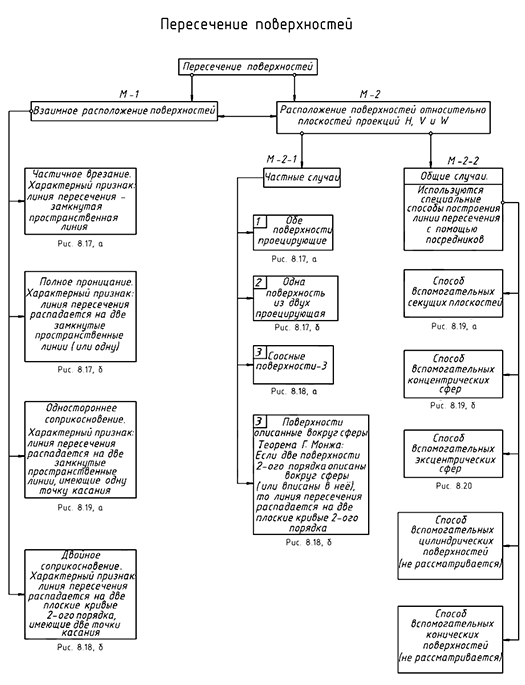
Структуризация материала восьмой лекции в рассмотренном объеме схематически представлена на рис. 8.16 (лист 1). На последующих листах 2-5 приведены иллюстрации к этой схеме для быстрого визуального закрепления изученного материала при повторении (рис. 8.17-8.20).

Эта теория взята со страницы лекций для 1 курса по предмету «начертательная геометрия»:

Возможно эти страницы вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник