Что такое площадь основания пирамиды

Площадь основания пирамиды: формулы для треугольных и четырехугольных правильных фигур

Вычисление площадей фигур является одной из приоритетных задач геометрии на плоскости и в пространстве. В данной статье рассмотрим объемную фигуру пирамиду. И покажем, какие формулы площади основания пирамиды следует применять для вычисления этой величины.

Что представляет собой пирамида?

Ответ на этот вопрос не столь очевиден, как многим может показаться. Когда люди слышат слово «пирамида», то в их воображении всплывает великое каменное сооружение египетских фараонов. Однако это лишь частный случай фигур этого класса.

Вам будет интересно: Образ русской женщины в классической литературе

Здесь изображен набор самых разных пирамид. Верхняя левая называется треугольной, поскольку ее основание является треугольником. Нижняя правая пирамида называется двадцатиугольной.

Правильные и неправильные фигуры

Мы выяснили, что такое основание фигуры. Тем не менее, до того как начать обсуждение формулы площади основания пирамиды, следует дать определение правильных и неправильных фигур этого класса.

Выше было упомянуто о вершине пирамиды. Она соответствует точке, где пересекаются все треугольные боковые грани фигуры. Если из вершины опустить перпендикуляр к основанию, то длина полученного отрезка будет соответствовать расстоянию от вершины до основания. Этот отрезок называется высотой фигуры.

Если высота пересекает многоугольник в его геометрическом центре, то пирамида называется прямой. Если основанием прямой пирамиды будет многоугольник, имеющий стороны одинаковой длины и равные между собой углы, то пирамида называется правильной. Соответственно, если какое-либо из названных условий не выполняется, то говорят о неправильной пирамиде.

Согласно описанной классификации, пирамида Хеопса является правильной четырехугольной, имеющей в основании квадрат.

Площадь основания правильной пирамиды

Если n-угольник является правильным, то формула площади основания пирамиды будет универсальной. Запишем ее:

Пирамида треугольная правильная

Равносторонний треугольник является основанием правильной пирамиды треугольной. Площадь основания ее можно определить, если применить записанную в пункте выше формулу для Sn. Учитывая, что n = 3, получаем:

S3 = n/4*a2*ctg(pi/n) = 3/4*a2*ctg(pi/3) = √3/4*a2

Зная длину основания a, можно рассчитать соответствующую площадь.

Любопытно отметить, что в треугольной пирамиде, которую часто называют тетраэдром, все четыре стороны являются треугольниками. В правильной фигуре в общем случае только одна из сторон представляет собой равносторонний треугольник (основание). Остальные грани являются треугольниками равнобедренными.

Четырехугольная пирамида правильная

Пожалуй, она является самой знаменитой среди класса пирамид. Формула для площади основания пирамиды четырехугольной правильной известна школьнику уже в начальных классах, поскольку речь идет о площади квадрата. Следуя общему подходу, воспользуемся выражением для Sn. Подставляя n = 4, получаем:

S4 = 4/4*a2*ctg(pi/4) = a2

Например, найдем площадь основания четырехугольной пирамиды Хеопса. Длина стороны ее основания составляет приблизительно 230 метров. Это означает, что соответствующая площадь равна 52,9 тыс. м2, что больше площади 10 футбольных полей.

Источник

Площадь основания пирамиды

Основание правильной пирамиды является правильный многоугольник — равносторонний треугольник, квадрат. Основанием пирамиды называют ту фигуру, над которой расположена вершина пирамиды.То есть это та грань пирамиды, которая не включает в себя ее вершину. Площадь основания пирамиды — это площадь этой плоской фигуры.

Площадь основания правильной пирамиды

Правильная пирамида может быть трех видов:

Соответственно у правильной треугольной пирамида основание — равносторонний треугольник. У правильной четырехугольной пирамиды основание — квадрат. В основании шестиугольной правильной пирамиды в основании лежит шестиугольник. Приведем формулы для нахождения площади основания пирамиды:

Площадь основания правильной треугольной пирамиды

В основании равносторонний треугольник — находим его площадь:

, где — сторона треугольника.

Основание треугольной пирамиды

Площадь основания правильной четырехугольной пирамиды

В основании правильной четырехугольной пирамиды лежит квадрат, площадь квадрата:

, где — сторона квадрата.

Основание четырехугольной пирамиды

Площадь основания правильной шестиугольной пирамиды

Это площадь правильного шестиугольника. Если известна сторона шестиугольника, то площадь правильного шестиугольника находится по формуле:

Основание шестиугольной пирамиды

Площадь основания любой пирамиды

Площадь основания любой пирамиды — это площадь ее основания.

Если в основании пирамиды треугольник, то формулы для нахождения площади любого треугольника вы можете посмотреть в статье «Площадь треугольника».

В основании пирамиды может лежать любой прямоугольник, любой многоугольник. Обычно в школьных задачах, в основании пирамиды часто лежит треугольник, редко прямоугольник. Задачи, в которых в основании пирамиды лежит пятиугольник, семиугольник или произвольных многоугольник, практически не встречаются. Хотя их можно увидеть в олимпиадных задачах.

Теперь давайте решим несколько задач для нахождения площади основания пирамиды

Примеры решения задач

Задача 1

Дана правильная треугольная пирамида. Сторона основания пирамиды равна 2. Найдите площадь основания пирамиды.

Решение: пирамида правильная и треугольная, значит, в основании равносторонний треугольник. Тогда площадь основания пирамиды находится по формуле: . Нам дана сторона , тогда

Ответ:

Задача 2

Теперь подсчитаем, сколько нам понадобится досок: .

Задача 3

Основанием пирамиды является прямоугольный равнобедренный треугольник, с катетом, равным 4. Найдите площадь основания пирамиды.

Решение: иными словами — нас просят определить площадь прямоугольного равнобедренного треугольника. Так как треугольник прямоугольный и равнобедренный, то один из катетов будет основанием треугольника, а другой — высотой. Определяем площадь по формуле:

.

Источник

Вычисление площади правильной треугольной пирамиды

Вычисление площади правильной треугольной пирамиды

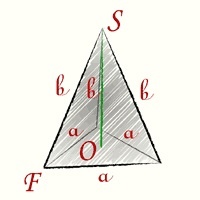
Правильная треугольная пирамида (тетраэдр) — это многогранник, в основании которого лежит правильный треугольник со сторонами a и боковыми гранями в виде равнобедренных треугольников с основанием a и сторонами b.

Площадь поверхности такой фигуры складывается из площадей основания многогранника и трех боковых граней. В записи на математический язык это выглядит так:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Нахождение площади основания пирамиды

Поскольку правильный тетраэдр основан на треугольнике, для определения площади основания рассматриваемого многогранника воспользуемся формулой нахождения площади треугольника:

Значение переменных: a — длина стороны равностороннего треугольника, h — его высота.

Далее произведем подстановку формулы вычисления высоты правильного треугольника и получим искомое выражение:

Вычисление площади боковых граней и полной поверхности

Боковые грани правильной треугольной пирамиды представлены тремя равнобедренными треугольниками. Выведем формулу расчета площади каждого из них из классического способа вычисления площади треугольника:

Здесь переменная a обозначает основание треугольника, h — его высоту.

Теперь выполним подстановку выражения, с помощью которого находится высота треугольника с одинаковыми бедрами, и получим уравнение определения площади равнобедренного треугольника:

В этом случае b — это боковые ребра треугольника, равные между собой.

Подставим в выражение (1) формулы (2) и (3) и получим уравнение, с помощью которого рассчитывается площадь полной поверхности правильного тетраэдра:

Примеры задач с решением

Задача

Дано

Правильный тетраэдр MABC с вершиной М. Высота основания AK=3 см.

∠MAB=∠MAC=∠MBA=∠MBC=∠MAB=∠MCA=∠MCB=45°. Необходимо вычислить площадь пирамиды MABC.

Решение

В основании правильного тетраэдра лежит равносторонний треугольник с известной длиной высоты. Применим свойство правильного треугольника, состоящее в следующем:

Преобразуем данное выражение так, чтобы вывести формулу стороны a:

Теперь найдем a:

Подставим полученное выражение в формулу нахождения площади основания правильного многогранника с тремя боковыми гранями:

Далее необходимо найти площадь боковых граней тетраэдра. Для этого произведем вычисление высоты MK. Так как угол между гранью и основанием пирамиды равен 45°, то ∠OKM=45°, следовательно:

По свойству правильного треугольника, отрезок OK равен радиусу вписанной в ΔABC окружности.

Найдем ее по соответствующей формуле:

Подставим найденную величину в отношение ОК к МК:

Из данной пропорции выведем выражение, по которому можно определить длину высоты MK:

Теперь, когда известны основание и высота равнобедренного треугольника, составляющего боковую грань пирамиды MABC, подставим значения в классическую формулу нахождения площади треугольника:

Суммируем площадь основания и боковых граней пирамиды:

Ответ, выраженный в квадратных сантиметрах: \(3\sqrt3+18\sqrt6\;(см^2)\)

Источник

Нахождение площади правильной пирамиды: формулы

В данной публикации мы рассмотрим, как можно вычислить площадь поверхности различных видов правильных пирамид: треугольной, четырехугольной и шестиугольной.

Правильная пирамида – это пирамида, вершина которой проецируется в центр основания, являющегося правильным многоугольником.

Формула площади правильной пирамиды

1. Общая формула

Площадь (S) полной поверхности пирамиды равняется сумме площади ее боковой поверхности и основания.

Боковой гранью правильной пирамиды является равнобедренный треугольник.

Площадь треугольника вычисляется по формулам:

1. Через длину основания (a) и высоту (h):

2. Через основание (a) и боковую сторону (b):

Формула площади основания правильной пирамиды зависит от вида многогранника. Далее мы рассмотрим самые популярные варианты.

2. Площадь правильной треугольной пирамиды

Основание: равносторонний треугольник.

Источник

Пирамида

Вершина пирамиды — точка, соединяющая боковые рёбра и не лежащая в плоскости основания.

Основание — многоугольник, которому не принадлежит вершина пирамиды.

Апофема — высота боковой грани правильной пирамиды, проведенная из ее вершины.

Высота — отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра).

Диагональное сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ основания.

Некоторые свойства пирамиды

1) Если все боковые ребра равны, то

– около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр

– боковые ребра образуют с плоскостью основания равные углы

Если боковые ребра образуют с плоскостью основания равные углы, то все боковые ребра пирамиды равны.

Если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые ребра пирамиды равны.

Виды пирамид

Для правильной пирамиды справедливо:

– боковые ребра правильной пирамиды равны;

– в правильной пирамиде все боковые грани — равные равнобедренные треугольники;

– в любую правильную пирамиду можно вписать сферу;

– около любой правильной пирамиды можно описать сферу;

– площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию.

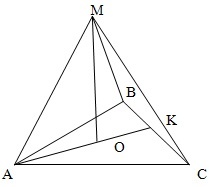
Тетраэдр – треугольная пирамида. В тетраэдре любая из граней может быть принята за основание пирамиды.

Источник