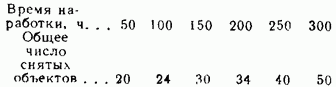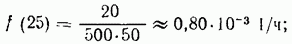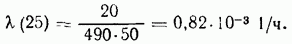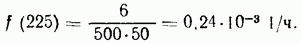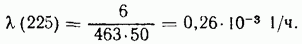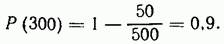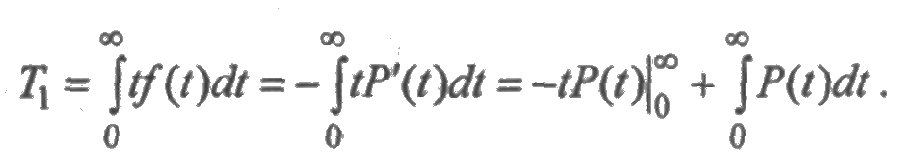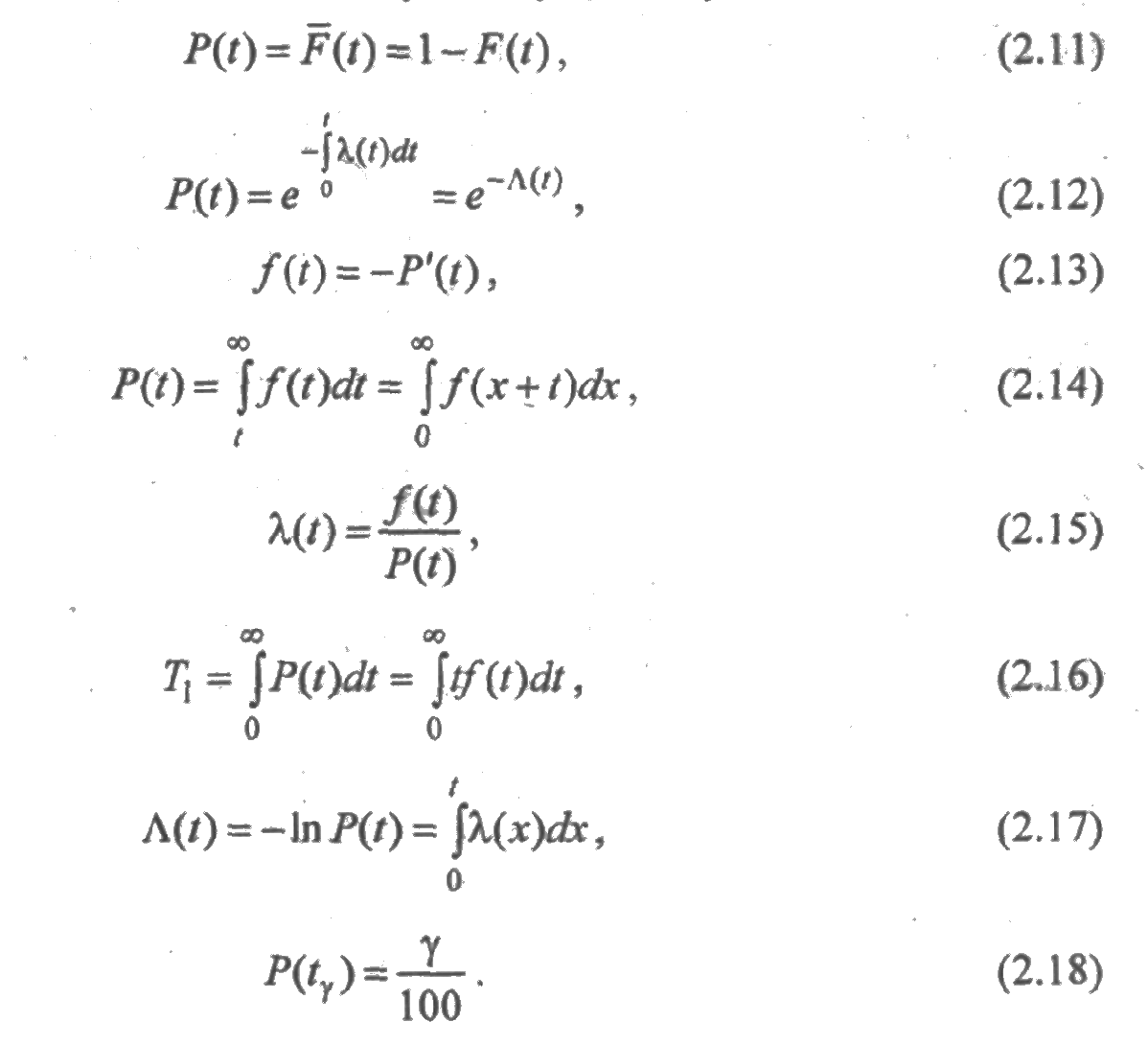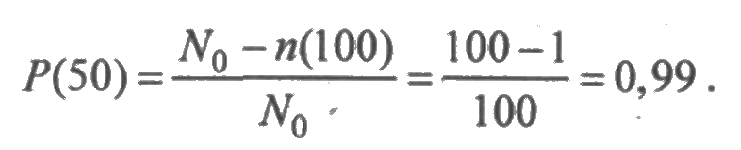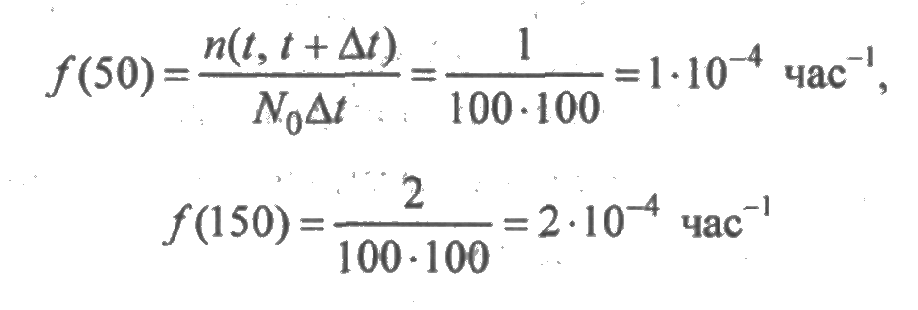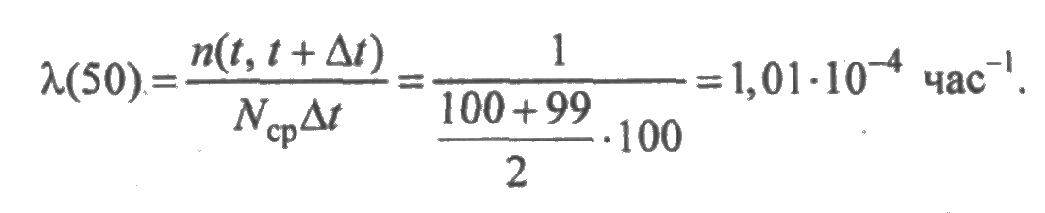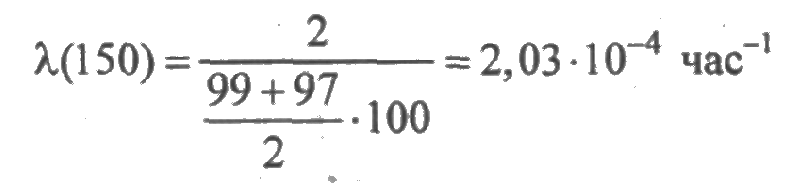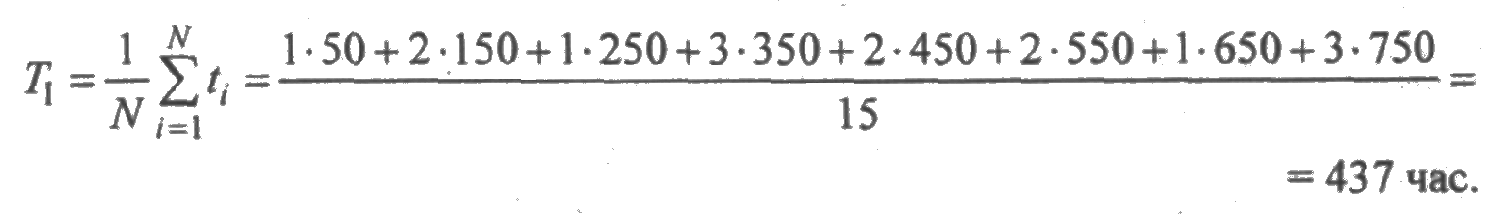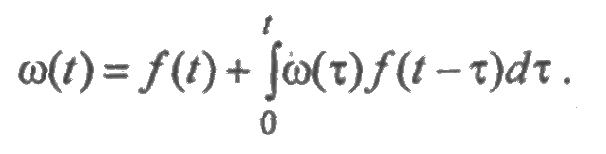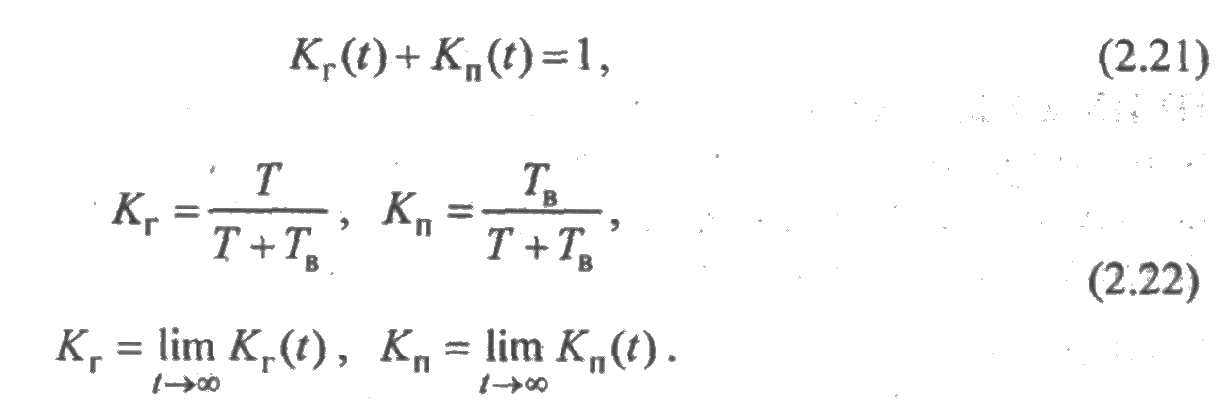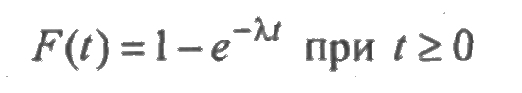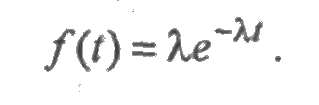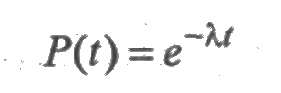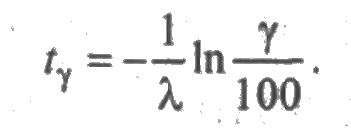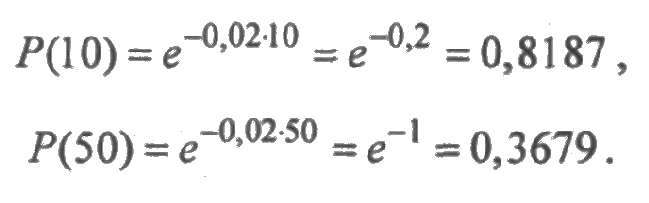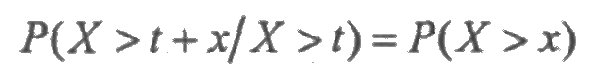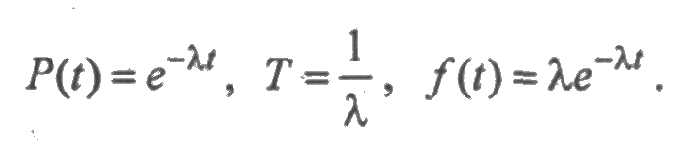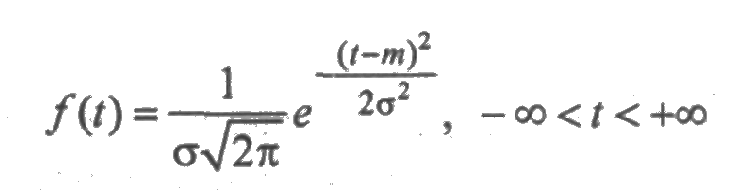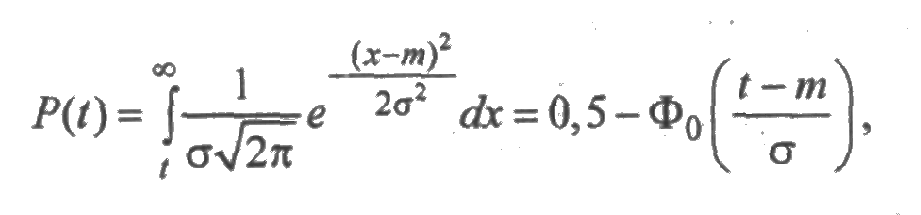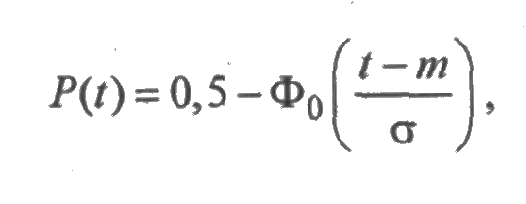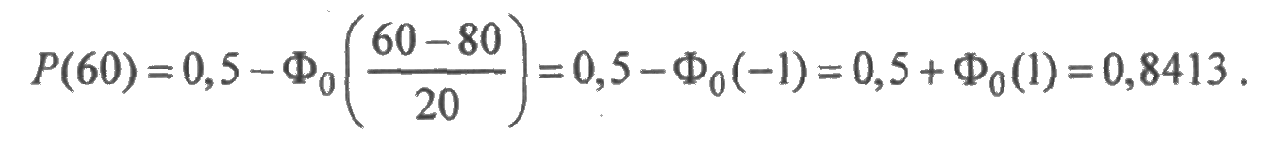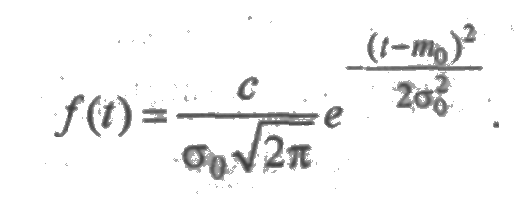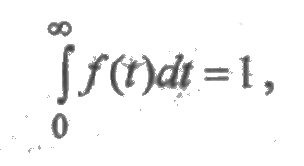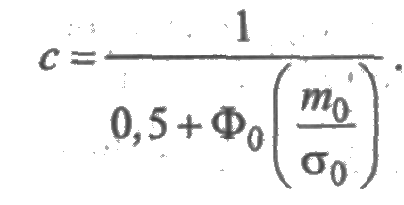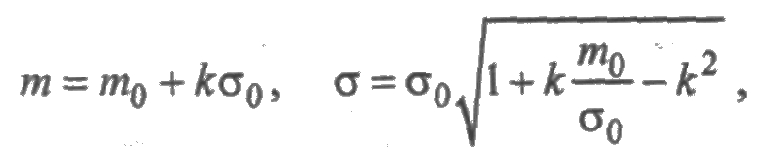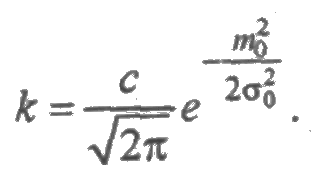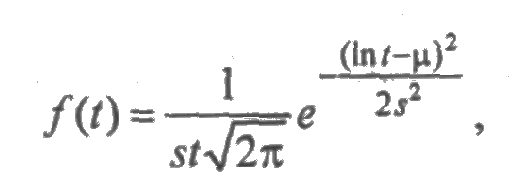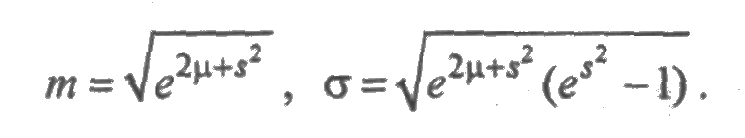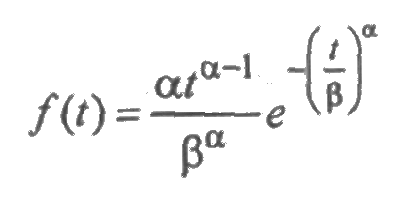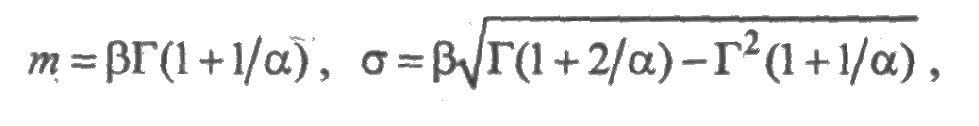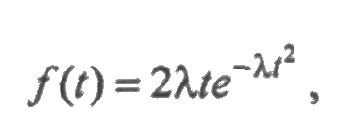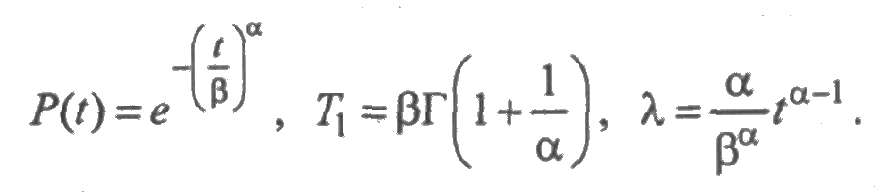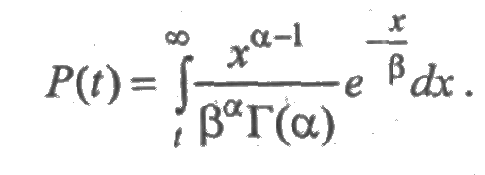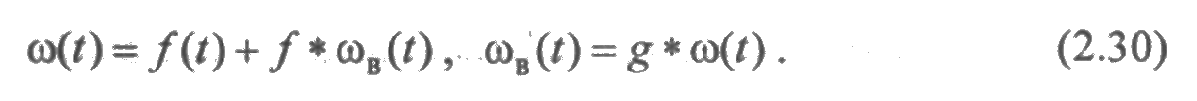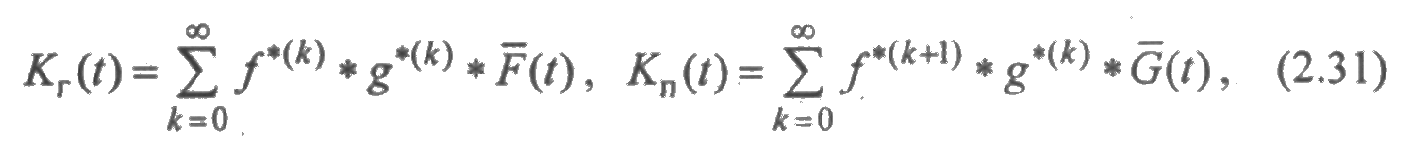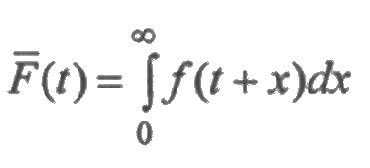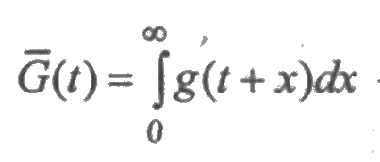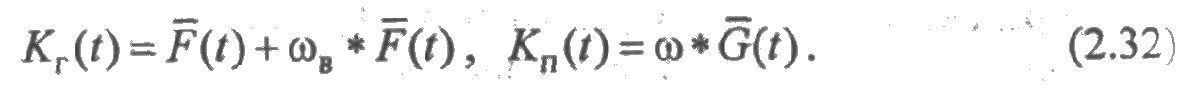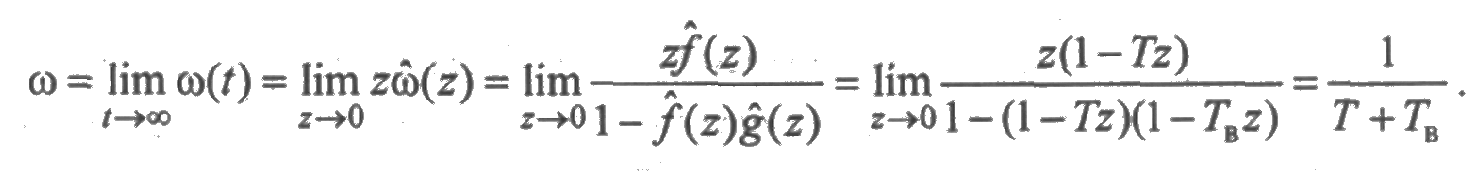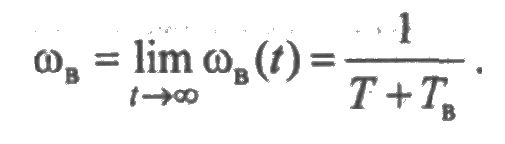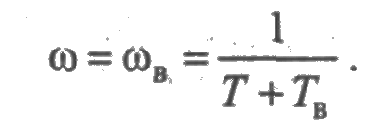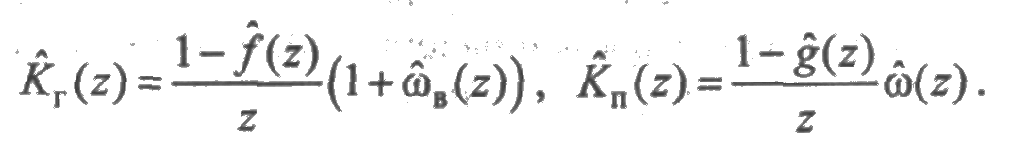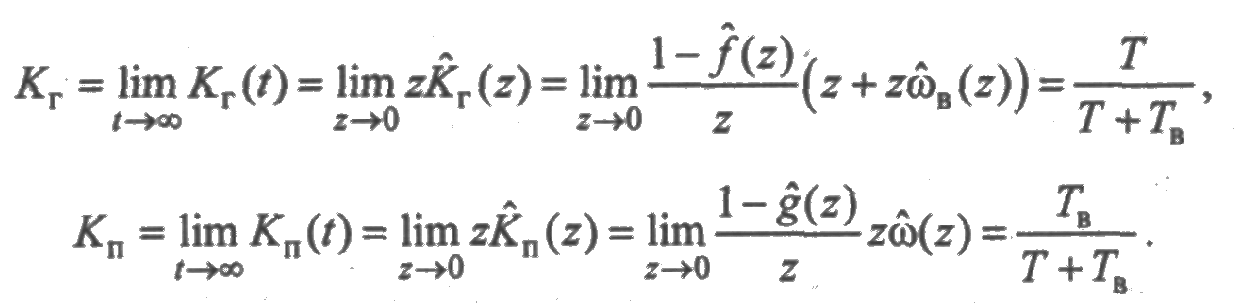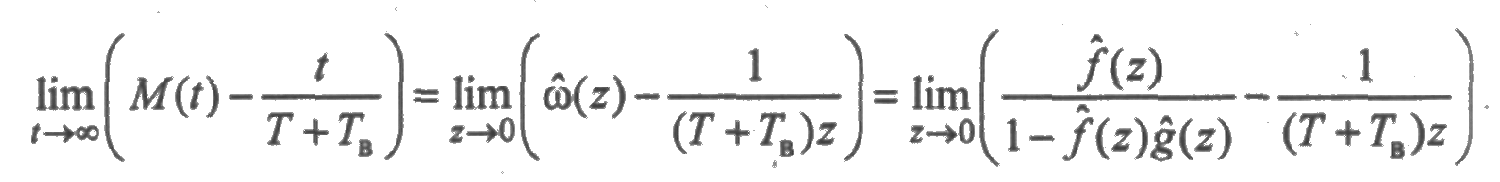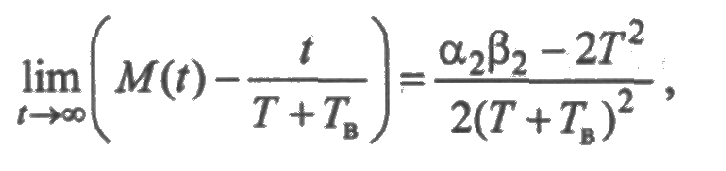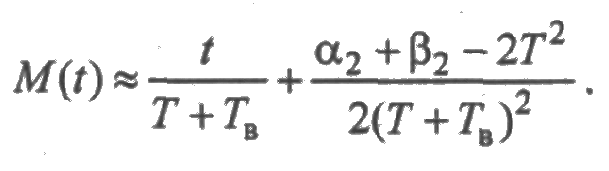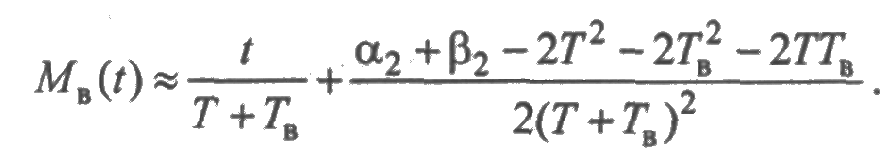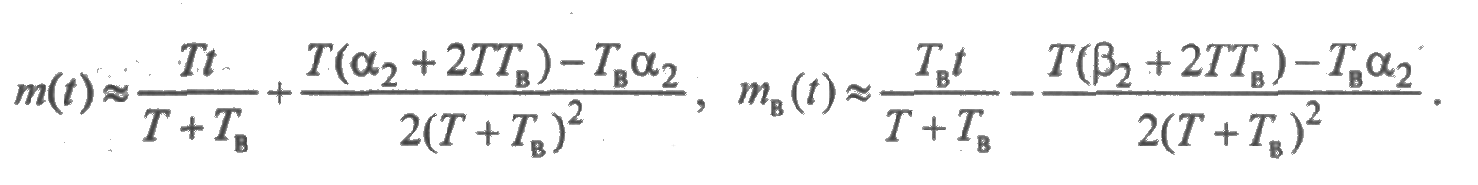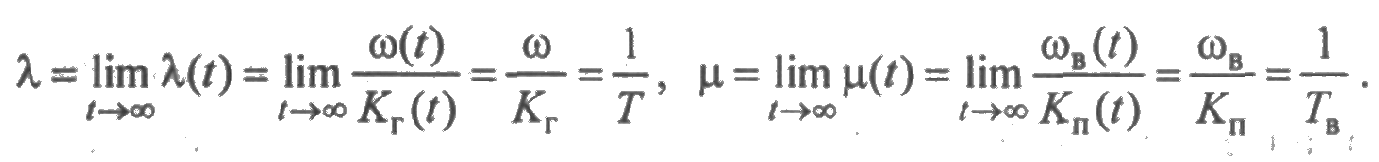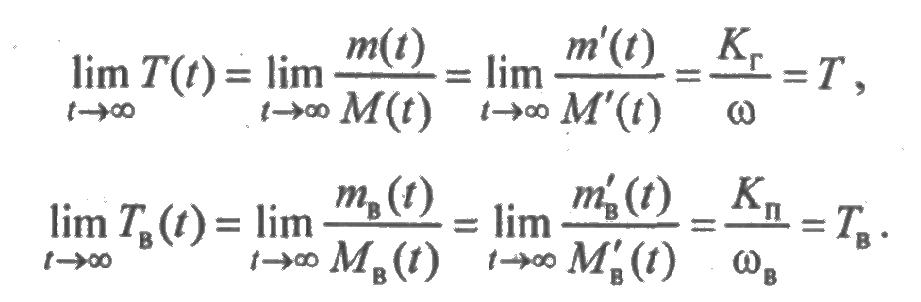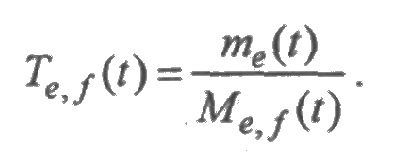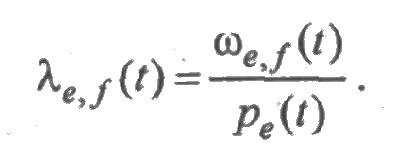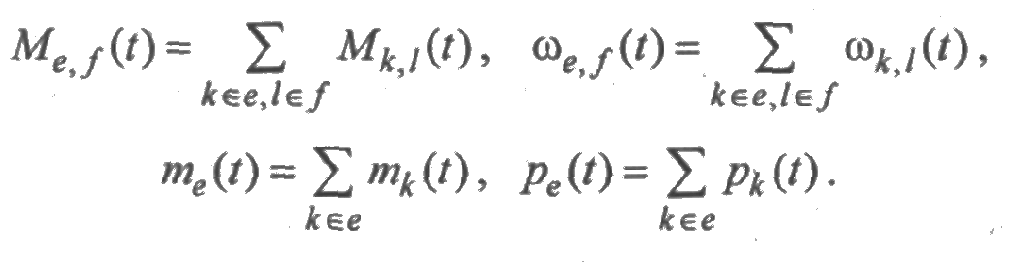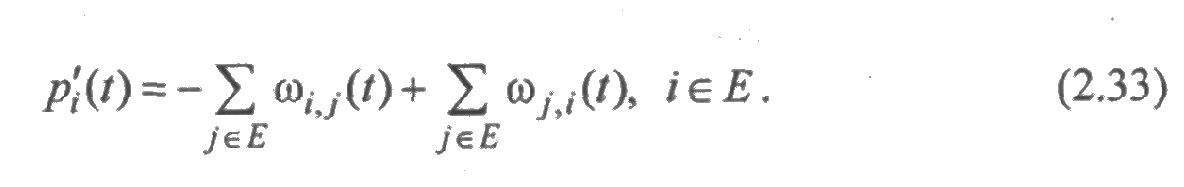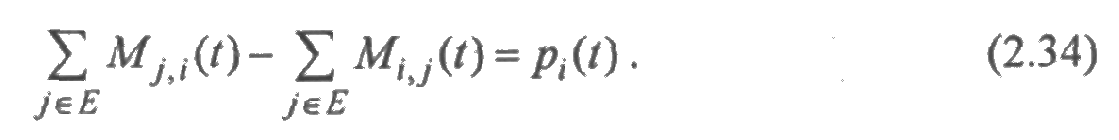Что такое плотность распределения отказов

Глава 03.1. Плотность распределения отказов (ПРО)

Статистическая оценка ПРО определяется отношением числа объектов N(t, t + T), отказавших в интервале наработки [t, t + T] к произведению общего числа объектов N на длительность интервала наработки T.

где( t, t + T) – оценка ВО в интервале наработки, т. е. приращение ВО за T.

Оценка ПРО представляет «частоту» отказов, т. е. число отказов за единицу наработки, отнесенное к первоначальному числу объектов.

Вероятностное определение ПРО следует из (10) при стремлении интервала наработки 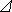T T0 и увеличения объема выборки N

ПРО по существу является плотностью распределения (плотностью вероятности) случайной величины T наработки объекта до отказа.

Поскольку Q(t) Является неубывающей функцией своего аргумента, то f(t) 0.

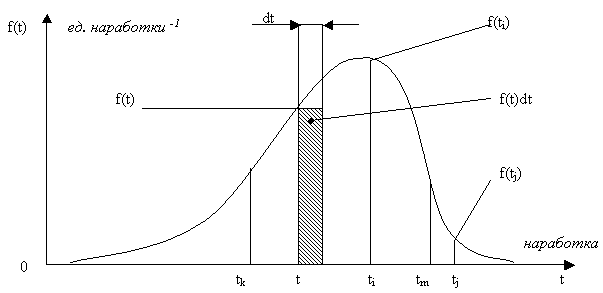
Один из возможных видов графика f(t) приведен на рис. 2.

Отложим на оси абсцисс некоторую наработку T и бесконечно малый интервал наработки шириной Dt, примыкающий к T.

Тогда вероятность попадания случайной величины наработки T на элементарный участок шириной Dt (с точностью до бесконечно малых высшего порядка) равна:

где f(t)dt – элемент ВО объекта в интервале [t, t + dt] (геометрически это площадь заштрихованного прямоугольника, опирающегося на отрезок Dt).

Аналогично вероятность попадания наработки T в интервал [tk, tm ] равна:

что геометрически интерпретируется площадью под кривой f(t), опирающейся на участок [tk, tm ].

Источник

ВЕРОЯТНОСТЬ БЕЗОТКАЗНОЙ РАБОТЫ, ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ И ИНТЕНСИВНОСТЬ ОТКАЗОВ

Время появления отказа t* рассматривают как случайную величину.

Вероятность безотказной работы за время t

(14.1)

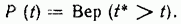
Символ Вер означает вероятность.

Пусть в начальный момент времени работает N0 изделий. Если к моменту времени наработки ti исправными оказались Nи(ti), а неисправными N*(ti) изделий, то статистическая оценка вероятности безотказной работы

(14.2)

(14.3)

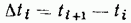
число отказавших изделий увеличилось на

(14.4)

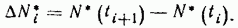
Вероятность отказа изделия за время Δti

(14.5)

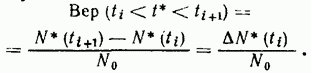
Если отнести вероятность отказа в промежутке Δti

к самому промежутку, то получим плотность распределения отказов

(14.6)

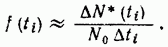
Более точно плотность распределения в момент t

(14.7)

(14.9)

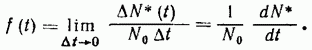
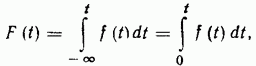
так как время до появления отказа — величина положительная. Из последнего соотношения следует:

(14.10)

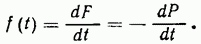
Интенсивность отказов λ(t) представляет собой число отказов в единицу времени, отнесенное не к первоначальному числу изделий, а к числу изделий, находящихся в эксплуатации в данный момент:

(14.11)

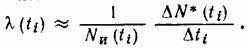
Если учесть, что ( по смыслу)

(14.12)

(14.13)

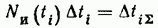
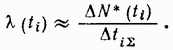
Более точно интенсивность отказов в момент времени t

(14.14)

Интенсивность отказов характеризует плотность вероятности отказов в ближайший промежуток времени, если до его начала отказ еще не произошел.

Интенсивность отказов и плотность вероятности отказов связаны соотношением

(14.15)

Равенство λ(t) можно записать его в виде:

, (14.16)

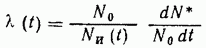
Пример. В эксплуатацию с ресурсом 300 часов выпущена партия из 500 объектов. Число снятых объектов после различной выработки характеризуется следующими данными:

Определить плотность вероятности и интенсивность отказов в период времени от 0 до 50 и от 200 до 250 и вероятность безотказной работы за ресурс.

Решение. За первый период снято 20 объектов и плотность вероятности отказов (для середины интервала — 25 ч).

интенсивность отказов (среднее число работающих объектов 490)

За период от 200 до 250 снято 6 объектов.

Плотность вероятности отказов

Вероятность безотказной работы за ресурс

Среднее времябезотказной работы.

Если f(t) — плотность вероятности

отказов, то среднее время безотказной работы

Интегрированием по частям находим и другую эквивалентную формулу

(14.17)

Источник

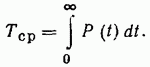
Плотность распределения отказов (ПРО)

Статистическая оценка ПРО определяется

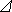
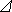
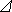
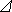
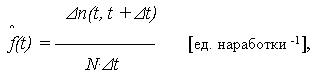отношением числа объектов n(t, t + t), отказавших в интервале наработки [t, t + t] к произведению общего числа объектов N на длительность интервала наработки t.

(9)

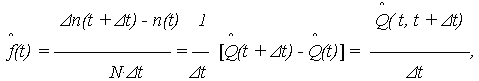(10)

где ( t, t + t) – оценка ВО в интервале наработки, т. е. приращение ВО за t.

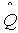
Оценка ПРО представляет «частоту» отказов, т. е. число отказов за единицу наработки, отнесенное к первоначальному числу объектов.

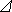
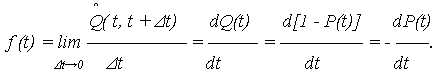Вероятностное определение ПРО следует из (10) при стремлении интервала наработки t t0 и увеличения объема выборки N

(11)

ПРО по существу является плотностью распределения (плотностью вероятности) случайной величины T наработки объекта до отказа.

Поскольку Q(t) является неубывающей функцией своего аргумента, то f(t) 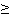0.

Один из возможных видов графика f(t) приведен на рис. 2.

Отложим на оси абсцисс некоторую наработку t и бесконечно малый интервал наработки шириной dt, примыкающий к t.

Тогда вероятность попадания случайной величины наработки T на элементарный участок шириной dt (с точностью до бесконечно малых высшего порядка) равна:

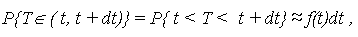(12)

где f(t)dt – элемент ВО объекта в интервале [t, t + dt] (геометрически это площадь заштрихованного прямоугольника, опирающегося на отрезок dt).

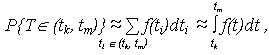(13)

ВО и ВБР можно выразить в функции ПРО.

Дата добавления: 2015-12-08 ; просмотров: 817 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Как вычисляется среднее время до отказа и вероятность безотказной работы?

Понятиям MTTF (Mean Time To Failure — среднее время до отказа) и другим терминам теории надежности посвящено большое количество статей, в том числе на Хабре (см., например, тут). Вместе с тем, редкие публикации «для широкого круга читателей» затрагивают вопросы математической статистики, и уж тем более они не дают ответа на вопрос о принципах расчета надежности электронной аппаратуры по известным характеристикам ее составных элементов.

В последнее время мне довольно много приходится работать с расчетами надежности и рисков, и в этой статье я постараюсь восполнить этот пробел, отталкиваясь от своего предыдущего материала (из цикла о машинном обучении) о пуассоновском случайном процессе и подкрепляя текст вычислениями в Mathcad Express, повторить которые вы сможете скачав этот редактор (подробно о нем тут, обратите внимание, что нужна последняя версия 3.1, как и для цикла по machine learning). Сами маткадовские расчеты лежат здесь (вместе с XPS- копией).

1. Теория: основные характеристики отказоустойчивости
Вроде бы, из самого определения (Mean Time To Failure) понятен его смысл: сколько (конечно, в среднем, поскольку подход вероятностный) прослужит изделие. Но на практике такой параметр не очень полезен. Действительно, информация о том, что среднее время до отказа жесткого диска составляет полмиллиона часов, может поставить в тупик. Гораздо информативнее другой параметр: вероятность поломки или вероятность безотказной работы (ВБР) за определенный период (например, за год).

Для того чтобы разобраться в том, как связаны эти параметры, и как, зная MTTF, вычислить ВБР и вероятности отказа, вспомним некоторые сведения из математической статистики.

Ключевое понятие теории надежности — это понятие отказа, измеряемое, соответственно, интервальным показателем
Q(t) = вероятность того, что изделие откажет к моменту времени t.
Соотвественно, вероятность безотказной работы (ВБР, в английской терминологии «reliability»):
P(t) = вероятность того, что изделие проработает без отказа от момента t₀=0 до момента времени t.
По определению, в момент t₀=0 изделие находится в работоспособном состоянии, т.е. Q(0)=0, а P(0)=1.

Оба параметра — это интервальные характеристики отказоустойчивости, т.к. речь идет о вероятности отказа (или наоборот, безотказной работы) на интервале (0,t). Если отказ рассматривать, как случайное событие, то, очевидно, что Q(t) — это, по определению, его функция распределения. А точечную характеристику можно определить, как
p(t)=dQ(t)/dt = плотность вероятности, т.е. значение p(t)dt равно вероятности, что отказ произойдет в малой окрестности dt момента времени t.

И, наконец, самая важная (с практической точки зрения) характеристика: λ(t)=p(t)/P(t)=интенсивность отказов.
Это (внимание!) условная плотность вероятности, т.е. плотность вероятности возникновения отказа в момент времени t при условии, что до этого рассматриваемого момента времени t изделие работало безотказно.

Измерить параметр λ(t) экспериментально можно путём испытания партии изделий. Если к моменту времени t работоспособность сохранило N изделий, то за оценку λ(t) можно принять процент отказов в единицу времени, происходящих в окрестности t. Точнее, если в период от t до t+dt откажет n изделий, то интенсивность отказов будет примерно равна
λ(t)=n/(N*dt).

Именно эта λ-характеристика (в пренебрежении ее зависимостью от времени) и приводится чаще всего в паспортных данных различных электронных компонент и самых разных изделий. Только сразу возникает вопрос: а как вычислить вероятность безотказной работы и при чем здесь среднее время до отказа (MTTF).

2. Экспоненциальное распределение
В терминологии, которую мы только что использовали, пока не было никаких предположений о свойствах случайной величины — момента времени, в который происходит отказ изделия. Давайте теперь конкретизируем функцию распределения значения отказа, выбрав в качестве нее экспоненциальную функцию с единственным параметром λ=const (смысл которого будет ясен через несколько предложений).

Дифференцируя Q(t), получим выражение для плотности вероятности экспоненциального распределения:
,
а из него – функцию интенсивности отказов: λ(t)=p(t)/P(t)=const=λ.

Что мы получили? Что для экспоненциального распределения интенсивность отказов – есть величина постоянная, причем совпадающая с параметром распределения. Этот параметр и является главным показателем отказоустойчивости и его часто так и называют λ-характеристикой.

Мало того, если теперь посчитать среднее время до первого отказа – тот самый параметр MTTF (Mean Time To Failure), то мы получим, что он равен MTTF=1/ λ.

Но это еще не все, потому, что для экспоненциального распределения особенно легко делать расчет систем, состоящих из множества элементов. Но об этом – в следующей статье (продолжение следует).

Источник

ЗАКОНЫ РАСПРЕДЕЛЕНИЙ ВРЕМЕНИ ДО ОТКАЗА

2.1. Что такое критерий и показатель надежности

Критерием называется признак (мерило), по которому оценивается надежность. Например, вероятность безотказной работы Р(t), интенсивность отказов λ(t), средняя наработка на отказ Т.

Основными характеристиками критериев являются:

— полнота оценки надежности технического объекта;

— непротиворечивость иным критериям качества объекта;

— возможность применения для оценки других, более общих показателей технического объекта (например, эффективность, безопасность, живучесть, риск).

Показателем надежности называется численное значение критерия. Например, вероятность безотказной работы в течение 1000 часов равна 0,95, т. е. Р(1000) = 0,95, или средняя наработка на отказ равна 687 часов, Т = 687 час.

Показатели задаются в технических требованиях на изделие, рассчитываются в процессе проектирования, оцениваются в процессе испытания и эксплуатации технического объекта.

Надежность является сложным физическим свойством, поэтому не существует одного обобщенного критерия и показателя, который бы достаточно полно характеризовал надежность техники. Только семейство критериев позволяет оценить надежность сложной технической системы. Выбор критериев зависит от типа технического объекта, его назначения и требуемой полноты оценки надежности.

Между показателями надежности существуют однозначные математические зависимости в виде формул. Поэтому при разработке семейства показателей надежности нельзя их задавать в виде равенств. Например, нельзя формулировать требования на надежность в таком виде: вероятность безотказной работы в течение 150 часов должна быть равна 0,97, а среднее время безотказной работы Т = 650 час. Такие требования могут оказаться противоречивыми.

Рассмотрим критерии надежности невосстанавливаемых и восстанавливаемых систем.

2.2. Критерии надежности невосстанавливаемых систем

Вероятность безотказной работы является убывающей функцией времени, имеющей следующие свойства:

По статистическим данным об отказах, полученным из опыта или эксплуатации, Р(t) определяется следующей статистической-оценкой:

(2.2)

где N₀ — общее число образцов, находящихся на испытании, N(t) — число исправно работающих образцов в момент времени t, n(t) – число отказавших образцов в течение времени t. Здесь и далее звездочкой обозначаются величины, полученные по статистическим данным.

Вероятность безотказной работы имеет следующие достоинства:

— характеризует надежность во времени, являясь интервальной оценкой;

— определяет многие важные показатели техники, например эффективность, безопасность, живучесть, риск;

— сравнительно просто вычисляется и определяется по статистическим данным об отказах техники;

— достаточно полно характеризует надежность невосстанавливаемой техники.

2.2.2. Плотность распределения времени безотказной работы (частота отказов)

Статистически f(t) определяется отношением числа отказавших образцов техники в единицу времени к числу испытуемых образцов при условии, что отказавшие образцы не восполняются исправными:

(2.3)

2.2.3. Интенсивность отказов

Интенсивностью отказов называется отношение плотности распределения к вероятности безотказной работы объекта:

(2.4)

Статистически интенсивность отказов есть отношение числа отказавших образцов техники в единицу времени к среднему числу образцов, исправно работающих на интервале [t,t+Δt]:

(2.5)

где -среднее число исправно работающих образцов на интервале [t,t+Δt]. Соотношение (2.5) для малых Δt следует непосредственно из (2.2) и (2.3).

На основе определения интенсивности отказов (2.4) имеет место равенство

(2.6)

Интегрируя (2.6), получим

Интенсивность отказов λ(t) является основным показателем надежности элементов сложных систем. Это объясняется следующими обстоятельствами:

— по известной интенсивности λ(t) наиболее просто оценить остальные показатели надежности как элементов, так и сложных систем;

— λ(t) обладает хорошей наглядностью;

— интенсивность отказов нетрудно получить экспериментально.

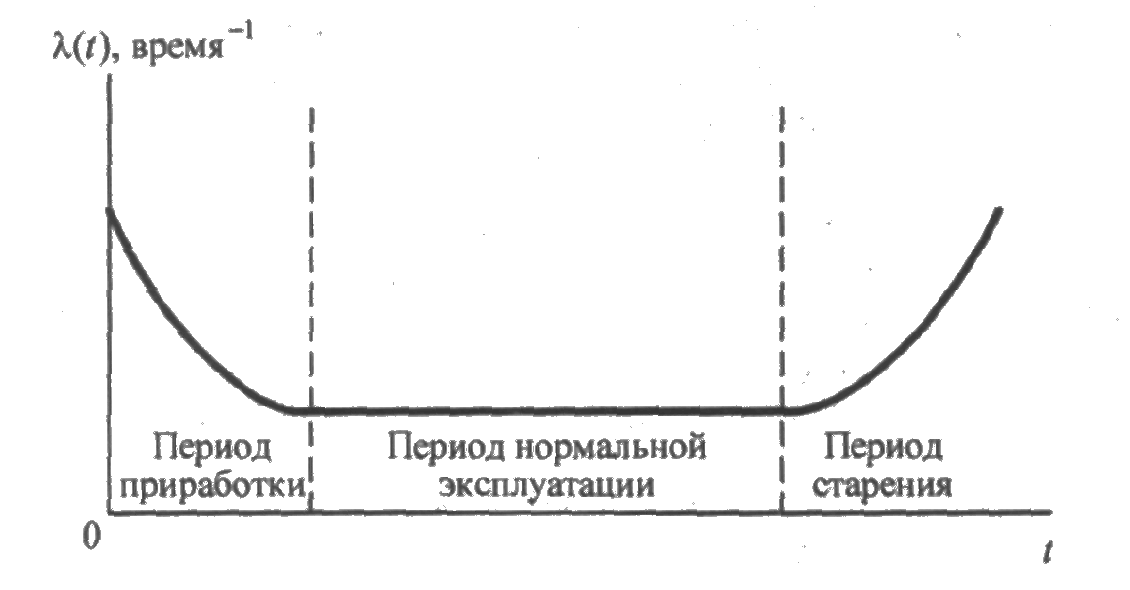
Опыт эксплуатации сложных систем показывает, что изменение интенсивности отказов λ(t) большого количества объектов описывается U-образной кривой (рис. 2.1). Время можно условно разделить на три характерных участка:

1. Период приработки.

2. Период нормальной эксплуатации.

3. Период старения объекта.

Период приработки объекта имеет повышенную интенсивность отказов, вызванную приработочными отказами, обусловленными дефектами производства, монтажа и наладки. Иногда с окончанием этого периода связывают гарантийное обслуживание объекта, когда устранение отказов производится изготовителем. В период нормальной эксплуатации интенсивность отказов практически остается постоянной, при этом отказы носят случайный характер и появляются внезапно, прежде всего из-за случайных изменений нагрузки несоблюдения условий эксплуатации, неблагоприятных внешних факторов и т.п. Именно этот период соответствует основному времени эксплуатации объекта. Возрастание интенсивности отказов относится к периоду старения объекта и вызвано увеличением числа отказов из-за износа, старения и других причин, связанных с длительной эксплуатацией.

2.2.4. Среднее время безотказной работы

Средним временем безотказной работы Т₁ называется математическое ожидание времени безотказной работы технического объекта:

По статистическим данным об отказах T₁ определяется следующей зависимостью:

(2.8)

где N₀ — число испытуемых образцов техники, t_i — время безотказной работы i-го образца.

Как математическое ожидание случайной величины с плотностью f(t), среднее время безотказной работы вычисляется по формуле:

Интегрируя (2.9) по частям, получим

Первое слагаемое равно нулю, т. к. Р(0)=1, Р(+∞) = 0, и тогда выражение для Т₁ будет иметь вид:

Итак, между показателями надежности существуют следующие зависимости:

ПРИМЕР 2.1. На испытании находилось N₀=100 образцов техники. Данные об их отказах приведены в первых трех строках табл. 2.1.

Необходимо вычислить показатели надежности: P(t), f(t), λ(t), T₁.

Решение.

Вычислим P(t). Будем иметь в виду, что нам достоверно неизвестен момент отказа на промежутке длины Δt. Поэтому будем предполагать, что отказы происходят в середине этого промежутка, т. е. в моменты времени: t = 50,150,250 и т. д. На первом интервале произошел один отказ. Тогда согласно (2.2) вероятность безотказной работы будет:

На втором участке произошло 2 отказа, а вcего за два периода длины Δt — 3 отказа. Тогда

Результаты расчетов приведены в четвертой строке табл. 2.1

Вычисления значений f(t) выполним по формуле (2.3):

и т. д. В данном случае число отказов на промежутке длины Δt не суммируется с числом отказов на предыдущих участках, т. к. функция f(t) является точечной. Результаты расчетов приведены в пятой строке табл. 2.1.

Вычислим значения λ(t), воспользовавшись выражением (2.5). На первом участке произошел один отказ, при этом в начале участка число исправных образцов N₀(0) = N₀ = 100, а в конце участка N₀(0) = N₀-1 = 99. Тогда

Аналогично на втором участке

и т. д. Значения λ(t) приведены в последней строке табл. 2.1.

Вычислим среднее время безотказной работы по формуле (2.8):

В данном случае испытания закончены при отказе 15 из 100 образцов.

Очевидно, что полученный результат существенно ниже действительного значения среднего времени безотказной работы как математического ожидания случайной величины.

2.3. Критерии надежности восстанавливаемых систем

Показателями надежности восстанавливаемых элементов и систем могут быть также показатели надежности невосстанавливаемых элементов. Это имеет место в тех случаях, когда система, в состав которой входит элемент, является неремонтируемой по условиям ее работы (необитаемый космический аппарат, аппаратура, работающая в агрессивных средах, самолет в процессе полета, отсутствие запчастей для ремонта и т. п.). Надежность восстанавливаемых объектов оценивают следующими показателями:

— Т — среднее время работы между отказами (средняя наработка на отказ);

— T_в — среднее время восстановления;

— ω(t) — параметр потока отказов;

— К_г(t) — функция готовности — вероятность того, что система исправна в момент t;

— К_п(t) — функция простоя— вероятность того, что в момент t система неисправна и восстанавливается;

— К_г — коэффициент готовности— вероятность того, что система будет исправной при длительной эксплуатации (стационарный режим);

— К_п — коэффициент простоя — вероятность того, что система будет неисправной при длительной эксплуатации.

Рассмотрим эти показатели несколько подробнее.

2.3.1. Среднее время работы между отказами и среднее время восстановления

Среднее время между отказами Т определяется отношением средней суммарной наработки к среднему числу отказов при длительной работе объекта. Среднее время восстановления Т_в определяется отношением среднего суммарного времени восстановления к среднему числу восстановлений при дли­тельной работе объекта. Данные определения обсуждаются далее в разд. 2.6.

По статистическим данным среднее время между отказами вычисляется по формуле:

(2.19)

где t_i — время между отказами i-го образца, полученное при условии, что испытания ведутся с восстановлением отказавших образцов техники или их заменой. В этом случае число испытуемых образцов техники N₀ остается постоянным.

4.1.1. Параметр потока отказов

Параметром потока отказов ω(t) называется производная (скорость изменения) среднего числа отказов объекта в момент t.

Статистически параметр потока отказов определяется как отношение числа отказавших образцов техники в единицу времени к числу образцов, поставленных на испытание при условии, что отказавшие образцы заменяются исправными или отремонтированными:

где п(t, t + Δt) — число отказавших образцов за промежуток времени [t, t + Δt], N₀ — число образцов, первоначально поставленных на испытания.

Параметр потока отказов обладает следующими свойствами:

— в случае экспоненциального закона времени работы объекта (см. разд. 2.4) с параметром λ, и мгновенного восстановления ω(t) ≡ λ;

— при мгновенном восстановлении предел, к которому стремится параметр потока отказов при t→∞, равен величине, обратной среднему времени безотказной работы, т. е.

— при мгновенном восстановлении параметр потока отказов и плотность распределения времени до отказа связаны следующим интегральным уравнением Вольтерра второго рода:

Это уравнение устанавливает зависимость между показателями надежности восстанавливаемой и невосстанавливаемой техники. Оно позволяет определить по статистическим данным об отказах восстанавливаемой техники в процессе ее эксплуатации показатели надежности невосстанавли­ваемой техники (см. гл. 11).

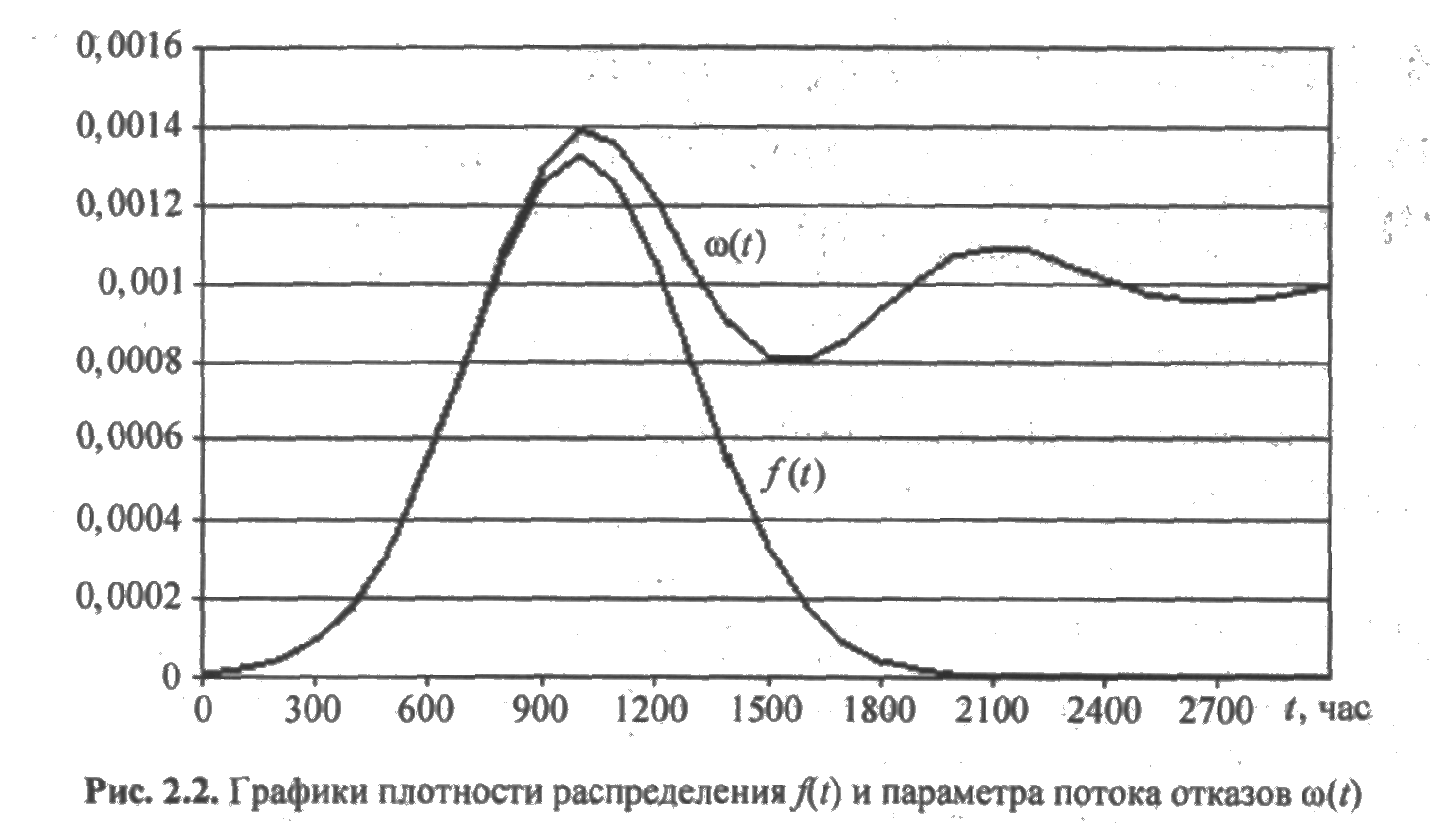
ПРИМЕР 2.2.Время до отказа объекта имеет нормальное распределение с математическим ожиданием Т = 1000 час и средним квадратическим отклонением s = 300 час. . Привести графическую иллюстрацию плотности распределения f(t) и параметра потока отказов ω(t).

Решение. Графики функций изображены на рис. 2.2. Параметр потока отказов ω(t) получен путем численного решения уравнения Вольтерра.

2.3.3. Функция готовности и функция простоя

Функцией готовности К_г(t) называется вероятность того, что восстанавливаемая система исправна в момент времени t.

Функцией простоя К_п(t) называется вероятность того, что в момент времени t система находится в отказовом состоянии (в ремонте).

Приведем основные зависимости между введенными показателями:

Данные показатели являются наиболее важными для восстанавливаемых элементов и систем. Другие, более специфические показатели, их определения и расчетные соотношения будут приведены в разд. 2.6.

2.4. Законы распределения времени до отказа, наиболее часто используемые в теории надежности

Приведем наиболее часто используемые в теории надежности параметрические семейства распределений случайной величины ξ, т.е. распределений, зависящих от одного или нескольких параметров, Функция

Плотность экспоненциального распределения задается как:

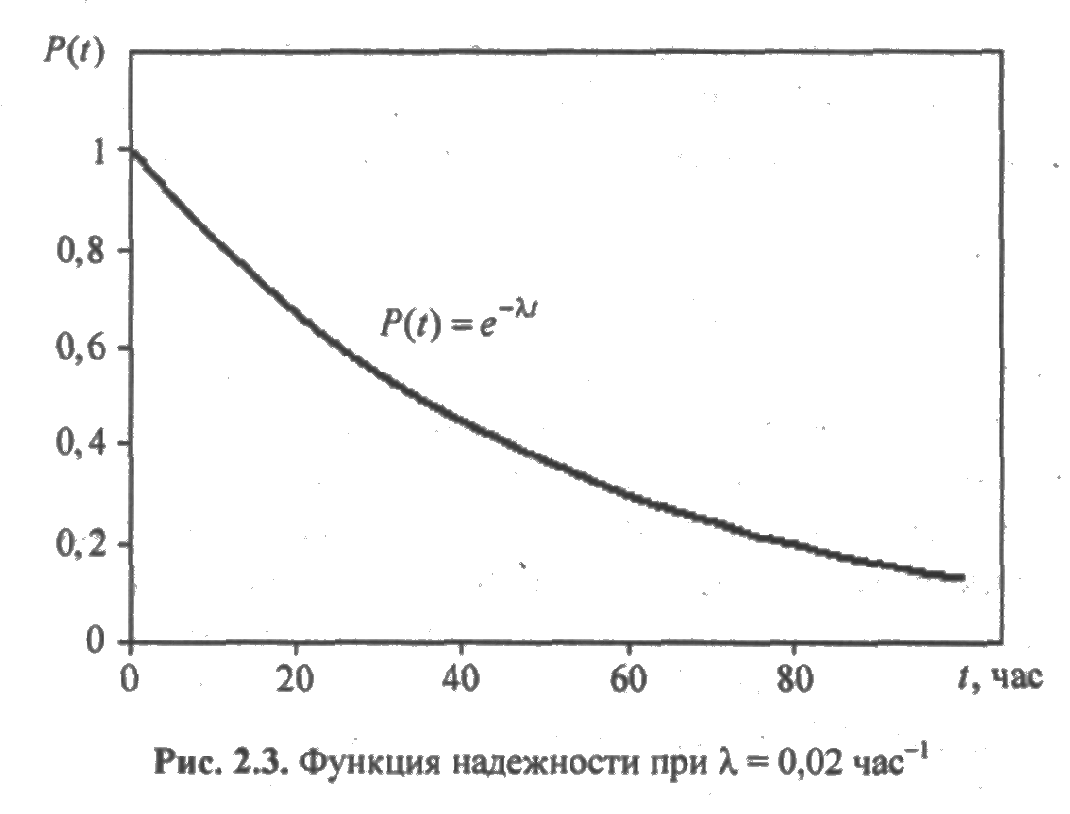
определяет вероятность безотказной работы за время t (рис. 2.3). В данном случае интенсивность отказов есть величина постоянная λ(t) = λ.

Функция ресурса для экспоненциального распределения является линейной Λ(t) = λt.

Величина γ-процентного ресурса определяется по формуле

Экспоненциальное распределение выделяется среди других распределение свойством «отсутствия памяти». Пусть X — время службы некоторого изделия с экспоненциальным законом распределения. «Отсутствие памяти» означает, что изделие, проработавшее время t, имеет такое же распределение, что и новое, только что начавшее работу. Математически это свойство выра­жается в виде следующего равенства:

для любых t, х≥0. Данное свойство как бы исключает износ и старение изделия.

Итак, при экспоненциальном законе отказов, на основании формул (2.11)— (2.18), между показателями надежности невосстанавливаемых систем существуют следующие зависимости:

Для характеристики постепенных отказов обычно используют другие законы распределения.

Нормальное распределение (распределение Гаусса) определяется плотностью

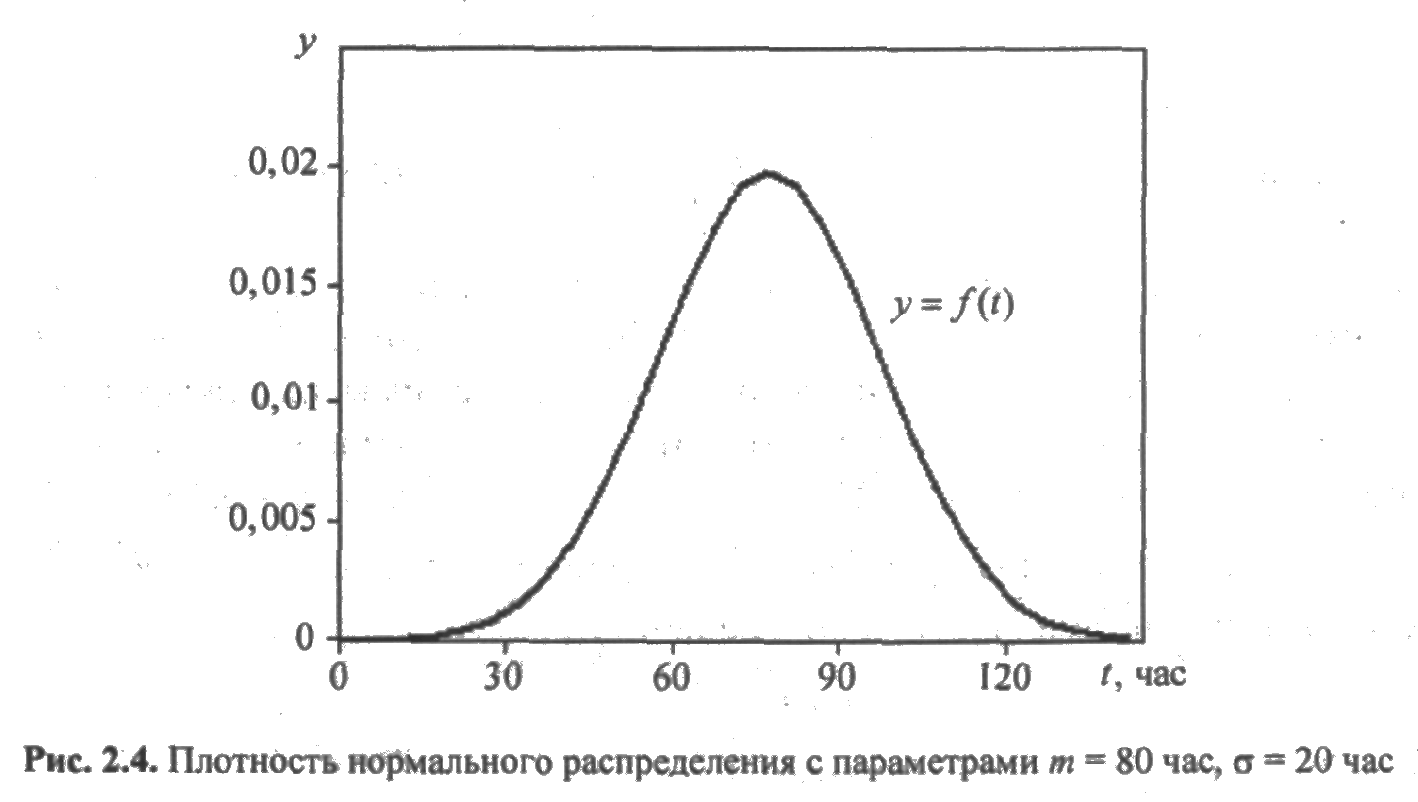
и зависит от двух параметров т и s, которые являются соответственно математическим ожиданием и средним квадратическим отклонением времени безотказной работы элемента. График плотности нормального распределения (кривая Гаусса) изображена на рис. 2.4.

Согласно закону больших чисел, распределение всегда подчиняется нормальному закону, если на изменение случайной величины оказывают влияние многие примерно равнозначные факторы. Нормальному распределению подчиняются ошибки измерения деталей, дальность полета снарядов и т. п. При большом времени работы элемента и наличии восстановления среднее число отказов имеет асимптотически нормальное распределение.

Для нормального распределения функция надежности вычисляется по формуле:

где 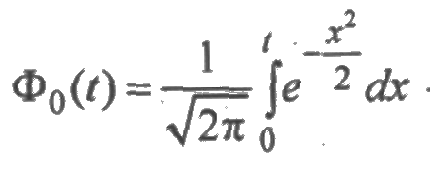— функция Лапласа, значения которой сведены в таблицы.

ПРИМЕР 2.4. Время безотказной работы элемента подчинено нормальному распределению с параметрами m=80 час и s=20 час. Найти вероятность того, что элемент проработает безотказно в течение 60 часов.

Решение. Так как для нормального распределения функция надежности равна

Отметим важное свойство нормального распределения: сумма независимых случайных величин, имеющих нормальное распределение, также распределена по нормальному закону. При этом параметры суммы выражаются через параметры слагаемых, а именно: математическое ожидание суммы равна сумме математических ожиданий, дисперсия суммы равна сумме дисперсий.

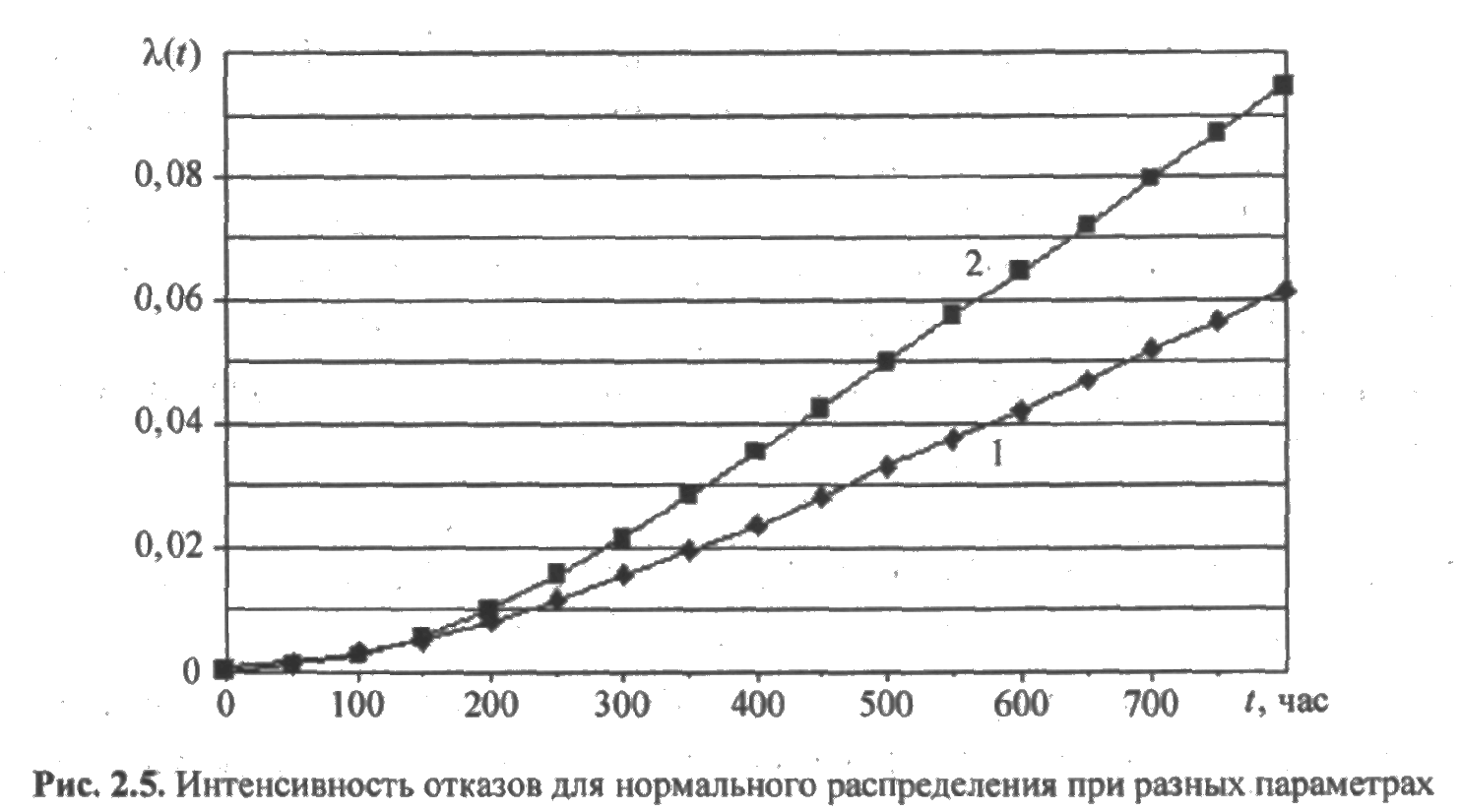
На рис. 2.5 представлены графики интенсивности отказов λ(t) для следующих параметров нормального распределения:

— т = 200 час и s = 100 час (кривая 1);

— т = 200 час и s = 80 час (кривая 2).

Усеченное нормальное распределение получается из нормального при огра­ничении интервала изменения случайной величины на промежуток [0,+∞). Плотность распределения записывается так же, как для нормального распределения, но с коэффициентом пропорциональности с:

Усеченное нормальное распределение зависит от двух параметров m₀ и s₀, где m₀ — значение случайной величины, соответствующее максимальному значению f(t) и называемое модой. Коэффициент с определяется из усло­вия нормировки:

Математическое ожидание и среднее квадратическое отклонение усеченного нормального распределения определяются через параметры m₀ и s₀ по формулам:

В логарифмически нормальном распределении логарифм случайной величины подчиняется нормальному закону с плотностью:

где μ и s — параметры распределения. Математическое ожидание и среднее квадратическое отклонение определяются в соответствии с формулами:

Логарифмически нормальное распределение применяют, например, для описания наработки подшипников качения. Вообще, оно удобно для описания случайных величин, представляющих собой произведение достаточно большого числа случайных величин, подобно тому, как нормальное распределение описывает сумму большого числа случайных величин.

Распределение Вейбулла является достаточно универсальным, благодаря возможности варьирования двух его параметров. Оно характеризуется плотностью распределения вероятностей:

с параметром формы α и параметром масштаба β. Математическое ожидание и среднее квадратическое отклонение выражаются через эти параметры следующим образом:

— гамма-функция. Универсальность распределения Вейбулла объясняется следующим: при α=1 распределение превращается в экспоненциальное; при α 1 интенсивность отказов возрастающая; при α=2 функция λ(t) линейная и распределение Вейбулла превращается в распределение Рэлея с плотностью:

при α=3,3 распределение Вейбулла близко к нормальному. Наряду с логарифмически нормальным распределением, оно хорошо описывает наработку деталей по усталостным разрушениям, наработку до отказа подшипников, а также используется для оценки надежности деталей и узлов машин, в частности автомобилей, подъемно-транспортных и других машин.

Зависимости между показателями надежности в случае распределения Вейбулла имеют вид:

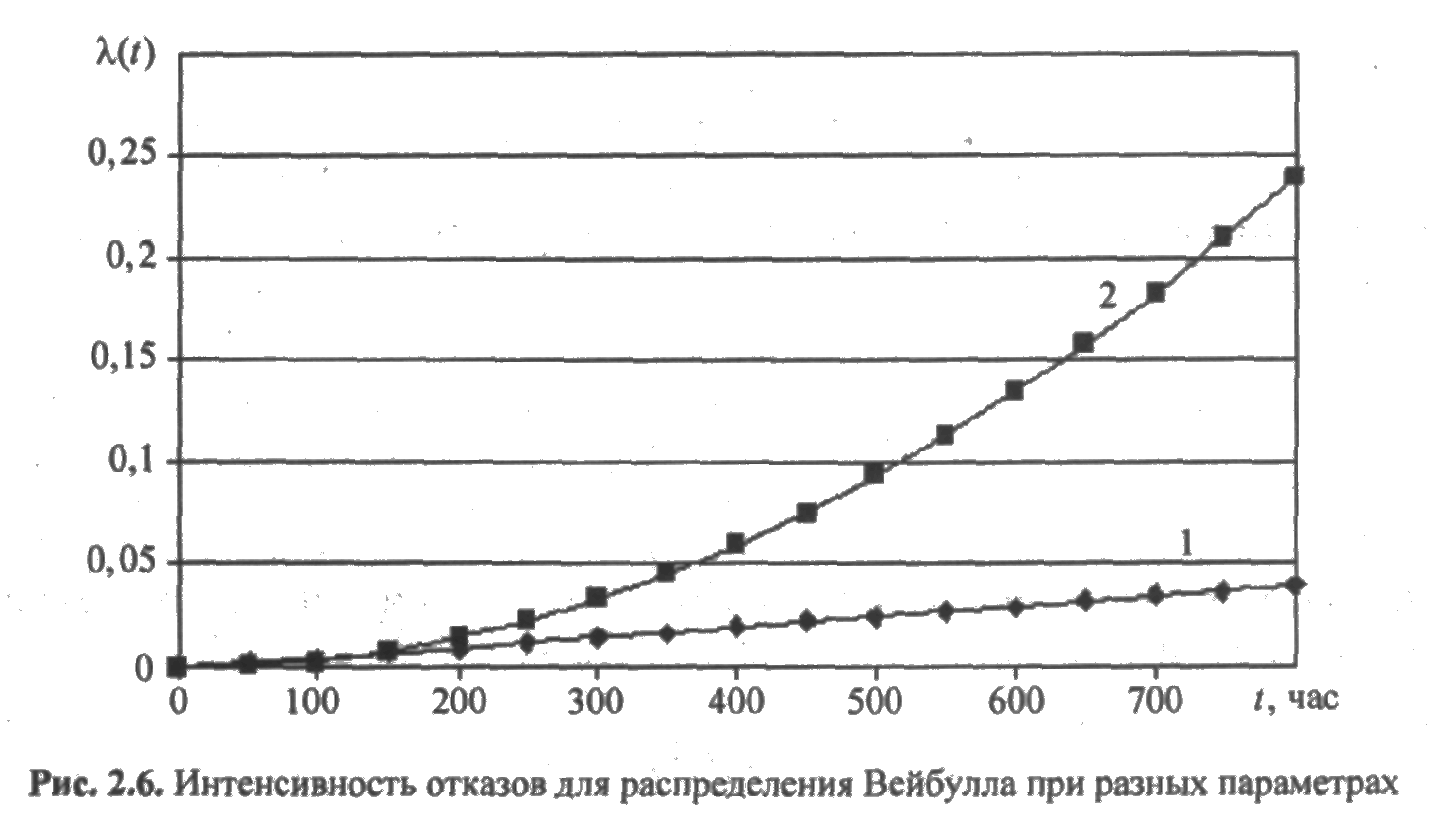
На рис. 2.6 представлены графики интенсивности отказов λ(t) для следующих параметров распределения Вейбулла:

— α = 2 и β = 200 час (кривая 1);

— α = 3 и β =200 час (кривая 2).

Гамма-распределение имеет плотность:

с параметрами α и β. Математическое ожидание и среднее квадратическое отклонение связаны с этими параметрами соотношениями:

Вероятность безотказной работы элемента, имеющего гамма-распределение, выражается через интеграл

Параметр α, характеризующий асимметрию гамма-распределения, определяет вид характеристик надежности. При α > 1 интенсивность отказа возрастает, при α t₀. Из временной диаграммы, изображенной на рис. 2.8, следует, что при 0 ( k ) k-кратную свертку функции f. Тогда из (2.23) получим сле­дующие выражения для параметров потоков:

откуда следуют зависимости

Для функций готовности и простоя из (2.27) и (2.28) будем иметь

вероятность безотказной работы элемента в течение времени t, а

вероятность того, что за время t элемент не будет восстановлен.

Из (2.31) следует, что

ПРИМЕР 2.6. Время до отказа элемента имеет нормальное распределение с параметрами α = 1000 час, s = 300 час. Время восстановления имеет нор­мальное распределение с параметрами b=10 час, r = 30 час. Требуется определить функцию готовности.

Решение. Вычислим функцию готовности по формуле (2.27). По свойству нормального распределения функции F_k,k(t) и F_k,k+1(t) также являются функциями нормального распределения с параметрами т_k = k(а + b), и m_k + α, соответственно. Поэтому, используя функцию Лапласа, получим

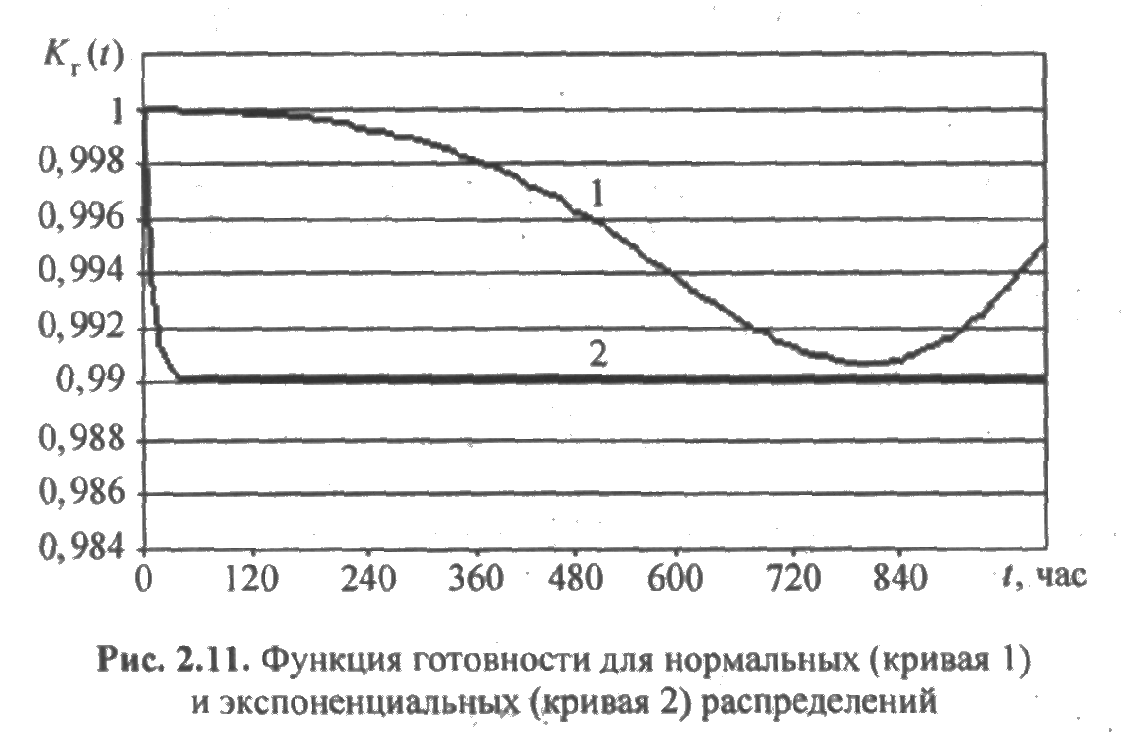
Расчеты, выполненные по этой формуле, позволяют построить график функ­ции готовности (рис. 2.11).

Для сравнения на этом же рисунке изображен график функции готовности, если время до отказа и время восстановления элемента имеют экспоненциальные распределения со средними а и b соответственно.

Различие двух кривых очевидно. Функция готовности для случая нормального распределения имеет колебательный характер, отсутствующий у системы с экспоненциальным законом распределения отказов и восстановлений. Стационарный режим в первом случае долго не наступает, во втором он наступает практически мгновенно.

2.6.2. Стационарные значения показателей надежности элемента

Получим предельные значения для показателей надежности восстанавливаемого элемента, предполагая, что с течением времени процесс функционирования элемента устанавливается и приобретает стационарный характер. Будем считать в дальнейшем, что f_k = f, g_k = g, k = 1, 2. с математическими ожиданиями T и T_в соответственно.

Наиболее удобным способом вычисления предельных соотношений является представление характеристик в виде преобразования Лапласа.

Из равенств (2.29) следует, что параметры потоков отказов и восстановлений в изображениях имеют вид:

Следовательно, по свойствам (4) и (5) преобразования Лапласа (см. разд. 2.5) получим:

Таким образом, стационарные значения параметров потоков отказов и восстановлений одинаковы и равны

Из (2.32) следует, что

Следовательно, коэффициенты готовности и простоя равны соответственно

Коэффициент готовности определяется только средним временем работы элемента до отказа и средним временем восстановления вне зависимости от законов распределения. Это означает, что К_г нельзя применять для оценки надежности технических систем кратковременного использования. Более полная информация о работе такой системы содержится в функции готовности (см. рис. 2.11).

Получим предельные соотношения для среднего числа отказов и восстановлений. Вычислим предел разности при t→∞:

Применяя свойство (5) преобразования Лапласа, подучим

где α₂ и β₂ — вторые начальные моменты случайных величин с плотностями f(t) и g(t) соответственно. Отсюда следует асимптотическая оцени среднего суммарного числа отказов:

Аналогично при t→∞ имеет место асимптотическая оценка среднего суммарного числа восстановлений:

Похожие рассуждения позволяют найти асимптотические оценки для средней суммарной наработки и среднего суммарного времени восстановления элемента:

Теперь легко найти предельные соотношения для интенсивностей потоков отказов и восстановлений:

Вычислим стационарные значения средней наработки между отказами и среднего времени восстановления:

Как и следует ожидать, для стационарного режима средняя наработка между отказами равна среднему времени безотказной работы элемента.

2.6.3. Показатели надежности невосстанавливаемой и восстанавливаемой техники

В разд. 2.6.1 были введены показатели надежности элементов. Определим теперь показатели надежности системы. Пусть Е — множество состояний системы, k, l ϵ E— любые два состояния множества Е. Введем в рассмот­рение следующие случайные процессы и свяжем с ними определенные функции.

Определим теперь случайные процессы и некоторые производные от их функции для подмножеств состояний множества Е, где е и f — любые непересекающиеся подмножества множества состояний Е:

ζ_e,f(t) — число переходов системы из состояний множества е в состояния множества f в течение времени [0,t], M_e,f(t) — математическое ожидание ζ_e,f(t), ω_e,f(t) = М’_e,f(t) — параметр перехода в момент времени t из множества состояний е в множество состояний f;

χ_e(t)— суммарное время пребывания системы в состояниях множества e в течение времени [0;t], т_е(t)— математическое ожидание χ_e(t), p_e(t) = m’_e(t)— вероятность пребывания в момент времени t в каком-либо состоянии множества е.

Случайные процессы ζ_e,f(t) и χ_e(t) являются базовыми, поскольку через них может быть получена вся информация о работе системы с позиции теории надежности. Так, например, математические ожидания этих процессов позволяют определить среднее время Т_e,f(t)_е>/(1) пребывания системы в множестве е до перехода в множество f в течение времени [0;t]:

Интенсивность перехода системы в момент времени t из множества е в множество f определяется отношением:

Укажем формулы связи между показателями, характеризующими множества состояний из Е и отдельные состояния множества Е:

2.6.4. Основное уравнение функционирования системы

Предположим, что процесс функционирования системы состоит из случайных времен пребывания в некоторых состояниях и мгновенных переходов одного состояния в другое. Случайное время пребывания в состоянии i характеризуется вероятностью p_i(t), а переход из состояния i в состояние j характеризуется параметром перехода ω_i,j(t). Тогда имеет место система уравнений:

Для доказательства обозначим через число входов в состояние i из любого другого состояния, а через — число выходов из состояния i в любое другое состояние в течение времени [0;t]. При фиксированном t это случайные величины, принимающие целочисленные значения. Рассмотрим 2 случая.

Случай 1. Состояние i не является начальным состоянием процесса функционирования.

Процесс не может выйти из состояния i, если он не оказался в этом состоянии, поэтому ≤ . После пребывания процесса в состоянии i в это состояние нельзя войти вновь до тех пор, пока процесс не выйдет из этого состояния, поэтому ≤ +1. Отсюда следует, что случайная величина — принимает только два значения: 0 или 1. При этом — = 1, если процесс пребывает в состоянии i. Вероятность этого события равна p_i(t). Аналогично — = 0, если процесс вышел из состояния i, но вновь еще не вошел в это состояние. Вероятность этого события равна 1- p_i(t). Следовательно, математическое ожидание случайной величины — равно p_i(t).

Случай 2. Состояние i является начальным состоянием процесса функционирования.

Очевидно, что здесь выполняется неравенство ≤ ≤ +1, поэтому случайная величина — может принимать только два значения 0 и 1 с вероятностями p_i(t) и 1-p_i(t) соответственно. Математическое ожидание этой случайной величины равно 1-p_i(t)

Источник