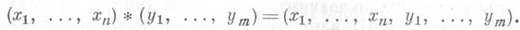Что такое полугруппа в алгебре

ПОЛУГРУППА

Теория П. принадлежит к числу сравнительно молодых областей алгебры. Первые исследования, посвященные П., относятся к 20-м гг. 20 в. и связаны с именем А. К. Сушкевича. Он, в частности, определил строение ядра (наименьшего идеала) конечной П., т. е. фактически строение конечной П. без собственных идеалов. Этот результат позднее был обобщен Д. Рисом (D. Rees) на произвольные вполне простые полугруппы и усовершенствован посредством введения понятия матрицы над группой (см. Рисовская полугруппа матричного типа). Теорема Риса, к-рую можно считать нек-рым аналогом теоремы Веддерберна о простых алгебрах, принадлежит к числу основных фактов теории П. Другие ранние исследования по теории П. принадлежат А. Клиффорду (A. Clifford), одним из первых значительных достижений к-рого было введение и изучение П., покрываемых группами; эти П. наз. теперь вполне регулярными, или клиффордовыми полугруппами. К кон. 50-х гг. 20 в. теория П. сформировалась в самостоятельную ветвь современной алгебры с богатой проблематикой, разнообразными методами и тесными связями с многими областями математики как собственно алгебраическими (в первую очередь, с теорией групп и теорией колец), так и другими, напр. функциональным анализом (П. операторов в банаховых пространствах), дифференциальной геометрией (П. частичных преобразований), алгебраич. теорией автоматов (П. автоматов).

Тогда F X относительно операции * является П.; она наз. свободной П. на множестве X. Всякая П. есть гомоморфный образ нек-рой свободной.

Всякая совокупность преобразований произвольного множества М, замкнутая относительно операции композиции (последовательного выполнения, наз. также суперпозицией), будет П. относительно этой операции; такова, в частности, совокупность всех преобразований множества М, наз. симметрической полугруппой на множестве М. Многие важные совокупности преобразований оказываются П., причем часто они не являются группами. С другой стороны, всякая П. изоморфна нек-рой П. преобразований. Таким образом, именно понятие П. оказывается наиболее подходящим для изучения в самом общем виде преобразований, и в большой степени через рассмотрение преобразований осуществляются связи теории П. с другими областями математики. При этом очень часто П. возникают как П. эндоморфизмов (см. Эндоморфизмов полугруппа).тех или иных рассматриваемых систем: пространств, алгебр, графов и т. д. К П. приводит также рассмотрение частичных преобразований и бинарных отношений относительно операции умножения.

Понятие регулярной полугруппы возникло по аналогии с понятием регулярного кольца. Класс регулярных П. принадлежит к числу наиболее интенсивно изучаемых в теории П. Он включает в себя следующие важные классы полугрупп: мультипликативные П. регулярных колец (и, в частности, П. всех матриц данного порядка над телом), симметрические П., П. всех частичных преобразований множеств, инверсные П., клиффордовы П. и, в частности, П. идемпотентов и вполне простые П., вполне 0-простые П. и др.

П., а частности конгруэнции. Так возникают, напр., разнообразные типы простых полугрупп и разнообразные условия конечности (см. Полугруппа с условием конечности, Периодическая полугруппа, Локально конечная полугруппа, финитно аппроксимируемая полугруппа, Минимальный идеал),II. с разными типами идеальных рядов и идеальных систем (см. Идеальный ряд, Нилъполугруппа>;принципиальную роль в исследовании многих вопросов теории П. играют Грина отношения эквивалентности.

При изучении строения П. важную роль играют различные конструкции, сводящие описание рассматриваемых П. к тем или иным «более хорошим» типам. Довольно часто в качестве последних выступают группы, и принцип описания «по модулю групп» распространен в теоретико-полугрупповых исследованиях, он проявился еще в упоминавшейся классич. теореме Риса, согласно к-рой всякая вполне 0-простая (вполне простая) П. изоморфна регулярной рисовской П. матричного типа над группой с нулем (группой). Группы участвуют в конструкциях, описывающих инверсные П., и в конструкциях, описывающих коммутативные архимедовы полугруппы с законом сокращения и без идемпотентов. Описание П. с многими условиями конечности сводится к группам с соответствующими условиями.

В исследованиях, связанных с рассмотрением подполугрупп, выделяется самостоятельное направление, посвященное изучению решеточных свойств П., т. е. взаимосвязей между свойствами П. и свойствами решеток их подполугрупп (см. Решетка подалгебр).

Широкое направление теории П. посвящено изучению различных вложений П. Истоки этого направления восходят к классич. проблеме вложения полугрупп в группы. О нек-рых задачах и результатах этого направления см. в ст. Расширение полугруппы.

Интенсивно развивается теория многообразий П.; об исследованиях в этом направлении см. в ст. Полугрупп многообразие. Начинает развиваться теория квазимногообразий П. (см. Алгебраических систем квазимногообразие).и нек-рых других классов П., близких в том или ином смысле к многообразиям.

Связи общей теории П. с конкретными П. осуществляются многими путями. Решаются проблемы абстрактной характеризации тех или иных важных конкретных П. (напр., П. преобразований: известно, в частности, несколько характеризации симметрических П.), описываются различные их абстрактные свойства. О нек-рых основных результатах, касающихся П. преобразований, см. Преобразований полугруппа. Изучаются изоморфизмы и гомоморфизмы абстрактных П. в различные конкретные П., прежде всего П. преобразований и II. матриц (см. Представление полугруппы). Исследованием гомоморфизмов П. в нек-рые числовые П., прежде всего в мультипликативную П. комплексных чисел, занимается теория характеров полугрупп.

К специальным разделам теории П. приводит рассмотрение П. с дополнительными структурами, согласованными с операцией умножения. Здесь следует, в первую очередь, отметить структуру топологич. пространстве (см. Топологическая полугруппа).и структуру порядка, частичного или линейного (см. Упорядоченная полугруппа).

Развивается и теория нек-рых видов обобщенных II. В первую очередь это алгебры с одной n-арной операцией, подчиненной обобщенному ассоциативному закону (их наз. n-ассоциативами, или п- полугруппами). Рассматриваются также алгебры с одной частичной ассоциативной бинарной операцией (одна из естественных ситуаций подобного рода возникает в теории категорий).

Источник

Полугруппа

Идентичность и ноль

Подполугруппы и идеалы

Если A является одновременно левым и правым идеалом, то он называется идеалом (или двусторонним идеалом ).

Подмножество, обладающее тем свойством, что каждый элемент коммутирует с любым другим элементом полугруппы, называется центром полугруппы. [4] Центр полугруппы на самом деле является подполугруппой. [5]

Гомоморфизмы и сравнения

Коэффициенты и деления

Следующие понятия [8] вводят идею о том, что одна полугруппа содержится в другой.

Оба эти отношения транзитивны.

Бесконечные обобщения коммутативных полугрупп иногда рассматривались разными авторами. [заметка 3]

Источник

Полугруппы можно рассматривать как частный случай магмы, где операция ассоциативна, или как обобщение группы, не требуя наличия элемента идентичности или инверсий. [примечание 1] Как и в случае групп или магм, полугрупповая операция не обязательна. коммутативный, так Икс·у не обязательно равно у·Икс; хорошо известный пример ассоциативной, но некоммутативной операции: матричное умножение. Если операция полугруппы коммутативна, то полугруппа называется коммутативная полугруппа или (реже, чем в аналогичный случай групп) его можно назвать абелева полугруппа.

Формальное изучение полугрупп началось в начале 20 века. Первые результаты включают Теорема Кэли для полугрупп реализуя любую полугруппу как полугруппа преобразований, в котором произвольные функции заменяют роль биекций из теории групп. Глубокий результат в классификации конечных полугрупп Теория Крона – Родса, аналогично Разложение Жордана – Гёльдера для конечных групп. Некоторые другие методы изучения полугрупп, например Отношения Грина, не похожи ни на что в теории групп.

Теория конечных полугрупп имела особое значение в теоретическая информатика с 1950-х годов из-за естественной связи между конечными полугруппами и конечные автоматы через синтаксический моноид. В теория вероятности, полугруппы связаны с Марковские процессы. [1] В других областях Прикладная математика, полугруппы являются фундаментальными моделями для линейные инвариантные во времени системы. В уравнения в частных производных, полугруппа связана с любым уравнением, пространственная эволюция которого не зависит от времени.

Источник

Полугруппы можно рассматривать как частный случай магмы, где операция ассоциативна, или как обобщение группы, не требуя наличия элемента идентичности или инверсий. [примечание 1] Как и в случае групп или магм, полугрупповая операция не обязательна. коммутативный, так Икс·у не обязательно равно у·Икс; хорошо известный пример ассоциативной, но некоммутативной операции: матричное умножение. Если операция полугруппы коммутативна, то полугруппа называется коммутативная полугруппа или (реже, чем в аналогичный случай групп) его можно назвать абелева полугруппа.

Формальное изучение полугрупп началось в начале 20 века. Первые результаты включают Теорема Кэли для полугрупп реализуя любую полугруппу как полугруппа преобразований, в котором произвольные функции заменяют роль биекций из теории групп. Глубокий результат в классификации конечных полугрупп Теория Крона – Родса, аналогично Разложение Жордана – Гёльдера для конечных групп. Некоторые другие методы изучения полугрупп, например Отношения Грина, не похожи ни на что в теории групп.

Теория конечных полугрупп имела особое значение в теоретическая информатика с 1950-х годов из-за естественной связи между конечными полугруппами и конечные автоматы через синтаксический моноид. В теория вероятности, полугруппы связаны с Марковские процессы. [1] В других областях Прикладная математика, полугруппы являются фундаментальными моделями для линейные инвариантные во времени системы. В уравнения в частных производных, полугруппа связана с любым уравнением, пространственная эволюция которого не зависит от времени.

Источник