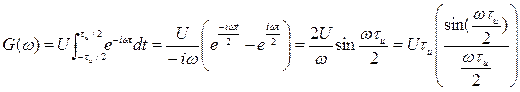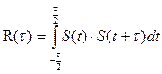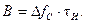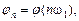Что такое база сигнала
База сигнала
База сигнала — это произведение эффективного значения длительности сигнала 


В простых случаях за эффективную ширину спектра можно принять ширину главного лепестка спектра. Длительность сигнала и ширина его спектра подчиняются соотношению неопределенности, гласящему, что база сигнала не может быть меньше единицы. Ограничений на максимальное значение базы сигнала не существует. То есть короткий сигнал с узким спектром существовать не может, а бесконечный сигнал с широким спектром — может (так называемый широкополосный сигнал, сигнал с большой базой). Примером такого рода может служить ЛЧМ-сигнал.
Литература
Полезное
Смотреть что такое «База сигнала» в других словарях:
база сигнала — Произведение ширины спектра сигнала на его длительность. См. processing gain. [Л.М. Невдяев. Телекоммуникационные технологии. Англо русский толковый словарь справочник. Под редакцией Ю.М. Горностаева. Москва, 2002] Тематики электросвязь, основные … Справочник технического переводчика
база — база: Поверхность или выполняющее ту же функцию сочетание поверхностей, ось, точка, принадлежащая заготовке или изделию и используемая для базирования. [ГОСТ 21495 76, таблица, пункт 2] Источник … Словарь-справочник терминов нормативно-технической документации
база радиочастотного сигнала — база сигнала Отношение ширины спектра модулированного радиочастотного сигнала к ширине спектра модулирующего сигнала. [ГОСТ 24375 80] Тематики радиосвязь Обобщающие термины сигналы Синонимы база сигнала … Справочник технического переводчика
База — База: В Викисловаре есть статья «база» База (хранилище) место для хранения товаров, например: «овощная база». Военная база … Википедия
База радиочастотного сигнала — 123. База радиочастотного сигнала База сигнала Источник: ГОСТ 24375 80: Радиосвязь. Термины и определения оригинал документа … Словарь-справочник терминов нормативно-технической документации
База радиочастотного сигнала — 1. Отношение ширины спектра модулированного радиочастотного сигнала к ширине спектра модулирующего сигнала Употребляется в документе: ГОСТ 24375 80 … Телекоммуникационный словарь
Сверхширокополосные сигналы — Сверхширокополосные (СШП) сигналы радиосигналы (СВЧ сигналы) со «сверхбольшой» шириной полосы частот. Применяются для сверхширокополосной радиолокации и сверхширокополосной радиосвязи. Содержание 1 Определение 2 Регулирование … Википедия
ГОСТ 24375-80: Радиосвязь. Термины и определения — Терминология ГОСТ 24375 80: Радиосвязь. Термины и определения оригинал документа: 304. Абсолютная нестабильность частоты радиопередатчика Нестабильность частоты передатчика Определения термина из разных документов: Абсолютная нестабильность… … Словарь-справочник терминов нормативно-технической документации
Сигнал — У этого термина существуют и другие значения, см. Сигнал (значения). Эта статья или раздел нуждается в переработке. Пожалуйста, улучшит … Википедия
Сигнал (техника) — Сигнал в теории информации и связи называется материальный носитель информации, используемый для передачи сообщений по системе связи. Сигналом может быть любой физический процесс, параметры которого изменяются в соответствии с передаваемым… … Википедия
Простые и сложные сигналы.
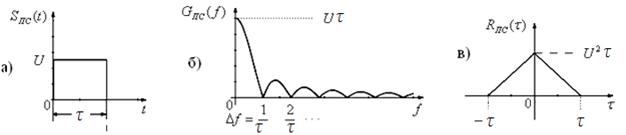
Простые сигналы. Простой сигнал – это одиночный импульс или последовательность импульсов, вида (2.2).
Для одиночного импульса мы будем иметь сплошной спектр (рис. 2.6,б), запись которого имеет вид
Размерность спектра (спектральной плотности) импульса будет определяться следующим образом 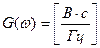
Полоса частот (рис. 2.6,б), где заключено 90% энергии сигнала равна:
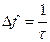
Чем уже корреляционная функция, тем легче, например, в радиолокации осуществить разрешение сигналов и определить параметры до цели по дальности, углу прихода, скорости движения объекта и т.д. Необходимо иметь как можно более острые КФ особенно при близко расположенных целях. Для заострения и укорачивания КФ казалось бы можно брать более короткие сигналы. Однако, энергия сигнала равна 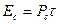
База простого сигнала равна 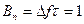
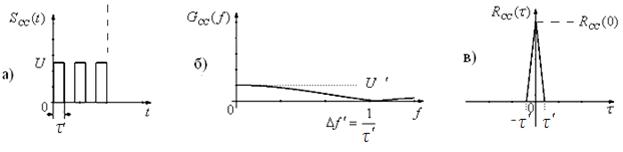
Сложные сигналы. Задача сложных сигналов, при той же исходной длительности сигнала τ сформировать узкую КФ, не снижая энергии сигнала. Информационный импульс длительностью τ разбивают на ряд импульсов одинаковой или разной длительностью (рис. 2.7,а).
Полоса частот, где заключено 90% сигнала равна (рис. 2.7,б):
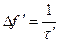
Поскольку энергия по отношению к простому сигналу не изменилась то корреляционная функция (рис. 2.7,в), для сохранения своей площади по отношению к простому сигналу будет лежать выше сложного сигнала.
В свою очередь База сложного сигнала будет равна
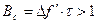
В большинстве случаев большой интерес представляют сигналы с Базой сигнала равной
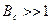
Выражение () определяет собой широкополосный шумоподобный сигнал (ШШС). У такого сигнала структура его приближается к белому шуму, а корреляционная функция стремиться к дельта функции, т.е стремиться в бесконечность.
В качестве сложных сигналов могут выступать коды Баркера и сигналы линейной частотной модуляции (ЛЧМ).
Линейные частотно-модулированные сигналы (ЛЧМ).Исходный сигнал остается той же длительности, но внутри него происходит линейное нарастание частоты с девиацией 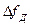
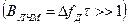
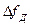
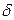
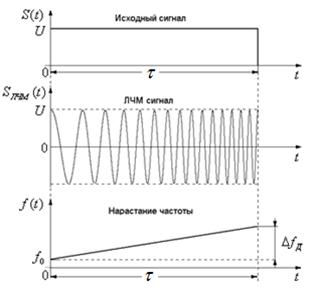 Рис.2.8 Рис.2.8 | 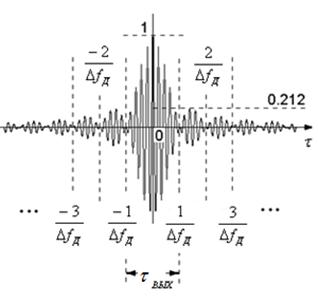 Рис.2.9 Рис.2.9 |
Линейный частотно-модулированный сигнал можно представить в виде
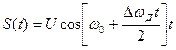 , , | (2.8) |
где 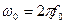
Ширина КФ определяется величиной 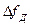
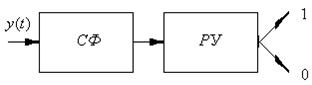
Прием ЛЧМ сигналов осуществляется на согласованный фильтр (СФ), на выходе которого имеется решающее устройство (РУ) (рис.2.10).
Согласованный фильтр представляет собой дисперсионную линию задержки с отводами на общий сумматор. Причем, учитывая разную скорость распространения различных гармонических колебаний, задержки отводов СФ выбраны так, чтобы по окончании импульса ЛЧМ все сигналы (гармоники) сложились бы одновременно в фазе. Это называется балансом фаз.
В результате такого одновременного сложения гармоник происходит сжатие сигнала. Коэффициентом сжатия находиться из выражения
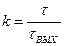 , , | (2.9) |
где τ – длительность передаваемого сигнала;
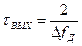
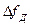
Чем больше коэффициент сжатия, тем уже пик КФ и тем выше разрешающая способность и помехоустойчивость системы. Кроме того, при большой базе можно увеличивать длительность сигнала и тем самым повышать его энергию, т.к. 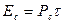
Основание КФ прямоугольного импульса длительностью 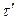
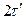

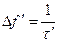
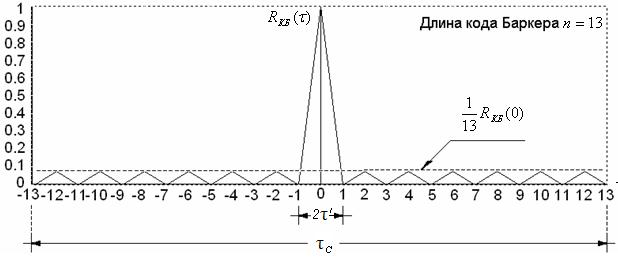
Если принять величину центрального пика КФ R(0)=1, то для выбранного значения n уровень боковых лепестков будет в n раз меньше (рис.2.12).
Прием сигналов Баркера осуществляется на СФ в виде дисперсионной линии задержки. Здесь так же сигналы складываются в фазе с приходом последней гармонической составляющей. В результате происходит сжатие принимаемого сигнала, энергия его возрастает в n раз в пределах сжатого сигнала, а боковые лепестки в n раз уменьшаются.
Коды Баркера позволяют не только увеличить разрешающую способность, но и увеличить помехоустойчивость и скрытность передачи, т.к. сигнал по своей структуре близок к ШШС.
Выводы: переход от простых к сложным сигналам позволяют обострить корреляционную функцию 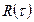
Как видно из рис. 2.13 зондирующий сигнал надо брать с острыми корреляционными функциями 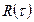
Вот почему выгоднее брать сигналы не простые, а сложные.
Дата добавления: 2015-04-16 ; просмотров: 495 ; Нарушение авторских прав
Соотношение длительности импульса и ширины полосы пропускания приемника
Рисунок 1. К определению базы сигнала для различных видов сигнала
Рисунок 1. К определению базы сигнала для различных видов сигнала
Соотношение длительности импульса и ширины полосы пропускания приемника
При разработке радиолокационного приемника возникает необходимость поиска компромисса при выборе требуемых значений его параметров. С одной стороны, полоса его пропускания должна быть как можно уже, чтобы уменьшить интенсивность проходящих в приемный тракт помех и шумов. С другой стороны, полоса пропускания должна быть достаточно широкой, чтобы обеспечить прием эхо-сигналов без искажений. При этом, чем короче используемые сигналы, тем шире должна быть полоса пропускания приемника, и тем лучшим будет разрешающая способность радиолокатора по дальности.
Пример: радиолокатор поиска AN/FPS-117 использует в качестве зондирующего сигнала ЛЧМ-сигнал с базой 75. Значение коэффициента сжатия импульса примерно такое же. Таким образом можно рассчитать разрешающую способность этого радиолокатора в ближней зоне (при использовании зондирующего сигнала длительности Τ= 100 мкс) — около 100 м.
Гауссов импульс имеет наименьшую возможную базу ¼. (Гаусоов импульс имеет огибающую в форме функции Гаусса и получается при помощи гауссовского фильтра. Такой фильтр характеризуется максимальной крутизной переходной характеристики и минимальной групповой задержкой). В некоторых устаревших радиолокаторах полоса пропускания приемника могла уменьшаться до этого значения, что соответствовало так называемому режиму ограничения приемника. Конечно, это приводит к увеличению внутренних потерь, поскольку уменьшается количество спектральных составляющих, а значит, и энергия принятого сигнала. Тем не менее, таким способом удавалось успешно подавлять помехи, частота которых отличается от несущей частоты зондирующего сигнала.
Чрезвычайно высокое значение базы (200 000) имеют зондирующие сигналы, используемые в радиолокаторе стратегического назначения AN/FPS-108 “Cobra Dane”.
Издатель: Кристиан Вольф, Автор: Андрій Музиченко
Текст доступен на условиях лицензий: GNU Free Documentation License
а также Creative Commons Attribution-Share Alike 3.0 Unported License,
могут применяться дополнительные условия.
(Онлайн с ноября 1998 года)
База непериодического сигнала
База сигнала – это один из важнейших параметров сигнала:
Произведение ширины спектра на длительность сигнала – это постоянная величина. В зависимости от величины B все сигналы делят на две группы:
1) Если база сигнала близка к единице, то такие сигналы называют простейшими.
2) Если база сигнала значительно больше единицы, то такие сигналы называют сложными.
Соотношение между длительностью сигнала и шириной его спектра
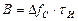
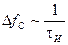
т. е. полоса спектра сигнала изменяется обратно пропорционально его длительности. Это значит, что, чем протяженнее сигнал во времени, тем уже его спектр, и наоборот, чем короче сигнал, тем шире его спектр.
Соотношение между спектром одиночного импульса и спектром периодической последовательности импульсов
 |
 |
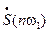
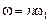
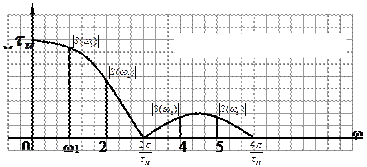
1. Определить спектральную плотность центрального одиночного импульса.
2. Записать формулу амплитудного спектра путем подставления в эту формулу вместо частоты ω частоту nω1, и по формуле 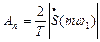
3. В формулу фазового спектра одиночного импульса вместо текущей частоты ω подставить текущую частоту nω1, и по формуле
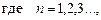
ВЫВОД. Непрерывный амплитудный спектр одиночного импульса является огибающей дискретного амплитудного спектра периодической последовательности импульсов. Непрерывный фазовый спектр одиночного импульса является огибающей дискретного фазового спектра периодической последовательности импульсов.
Продемонстрируем все вышесказанное на примере. В качестве сигнала возьмем импульсы:

 |
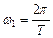
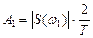
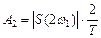
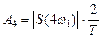
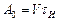
CDMA: расширение спектра
Каждой мобильной базовой станции в технологии CDMA выделяется своя уникальная кодовая последовательность, отличающая ее от других и одновременно используемая для повышения помехоустойчивости и обеспечения безопасности.
В эфире такой сигнал занимает полосу частот, значительно превышающую по ширине полосу частот исходного узкополосного сигнала.
Одно из фундаментальных понятий, определяющее помехоустойчивость и эффективность системы CDMA, — «база сигнала» (в англоязычной литературе используется термин «processing gain»). Физический смысл этого понятия — увеличение полосы частот передаваемого сигнала относительно исходного (измеряется в децибелах). Для систем с расширенным спектром база сигнала определяется как отношение ширины полос излучаемого и исходного (информационного) сигналов. Однако чаще величина базы сигнала (В) вычисляется как произведение ширины спектра (F) на длительность элементарного символа (Т). Для широкополосных сигналов база значительно превышает 1 (В>>1). Ясно, чем шире полоса частот в эфире и ниже скорость входного сигнала, тем больше база сигнала и, соответственно, выше помехоустойчивость.
Однако важно понимать, что база сигнала — это характеристика не всей CDMA-системы, а только ее отдельного канала. Поясним сказанное на примере. Так, при чиповой скорости 1,2288 Мчип/с (IS-95) и информационной скорости 9,6 кбит/c база сигнала равна 21,1 дБ (1,2288 x 10 3 /9,6 = 128). Для других значений скоростей передачи, используемых в стандартах IS-95 и cdma2000 (См. «Сети», 2000, № 1, с. 19), база сигнала пропорциональна скорости его передачи (таблица).
База сигнала для различных скоростей передачи информации (чиповая скорость — 1,2288 Мчип/с)
| Показатель | База сигнала, дБ |
| Скорость передачи RS1, кбит/с | |
| 1,5 | 23,1 |
| 2,7 | 26,6 |
| 4,8 | 24,0 |
| 9,6 | 21,1 |
| Скорость передачи RS2, кбит/с | |
| 1,8 | 28,3 |
| 3,6 | 25,3 |
| 7,2 | 22,3 |
| 14,4 | 19,3 |
Возможность адаптации системы к различным скоростям передачи обеспечивается за счет применения так называемых каналообразующих кодов (channelization code). Принцип их генерации можно проиллюстрировать (рис. 1) схемой кодового дерева для ортогональных кодов переменной длины (Orthogonal Variable Spreading Factor, OVSF).
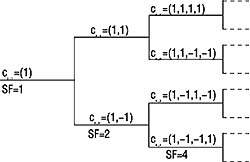 |
| Схема генерации OVSF-кодов для трух уровней |
На каждом уровне этого кодового дерева определены свои кодовые слова, длина каждого из которых равна коэффициенту расширения спектра (SF). Полное кодовое дерево содержит 8 уровней (последний, восьмой, соответствует коэффициенту SF=256 ).
Структура кодового дерева такова, что на каждом последующем уровне удваивается возможное число каналообразующих кодов. Так, если на уровне 2 образуется только 2 кода (SF=2), то на уровне 3 генерируется уже 4 кодовых слова (SF=4) и т.д. Ансамбль кодов OVSF не является фиксированным, а зависит от коэффициента расширения SF, т. е. фактически от скорости передачи по каналу.
Сейчас в большинстве CDMA-систем, в том числе основанных и на широко известном стандарте IS-95, используется метод расширения спектра прямой последовательностью DS-CDMA (Direct Sequence CDMA). Схема «работы» метода DS-CDMA и качественные изменения сигнала и помех показаны на рис. 2.
В передатчике узкополосный информационный сигнал (А на рис. 2) умножается на опорную псевдошумовую N-символьную последовательность, а полученный сигнал модулируется методом BPSK или QPSK (прямая операция). База результирующего сигнала равна числу символов псевдослучайной последовательности (B = N). При этом использование шумоподобных сигналов с высокой тактовой частотой приводит к тому, что исходный узкополосный сигнал «размазывается» в широкой полосе (Б на рис. 2) и становится меньше уровня шума.
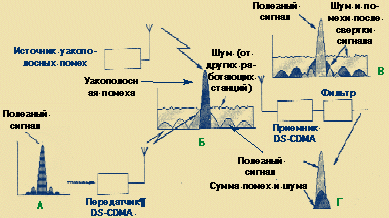 |
| Схема расширения спектра с помощью прямой последовательности: А — информационный сигнал; Б — сигнал на входе приемника; В — сигнал на выходе приемника; Г — выходной сигнал (после фильтра) |
В приемнике исходный сигнал восстанавливается с помощью псевдослучайной последовательности известной структуры (обратная операция). Иные сигналы, поступающие на данный приемник, воспринимаются как шум (В на рис. 2).
Аналогичным образом происходит подавление мощных узкополосных помех от других работающих передатчиков. В приемнике такая помеха тоже «размазывается» в широкой полосе частот и после фильтрации лишь незначительно ухудшает качество связи (Г на рис 2). При дальнейшей цифровой обработке помехи можно подавить полностью.
Кроме наиболее часто применяемого метода DS-CDMA существуют и другие технологии расширения спектра, например с помощью нескольких несущих — MC-CDMA (Multi-Carrier CDMA) или скачкообразной перестройки частоты — FH-CDMA (Frequency Hopping CDMA). Особенности этих технологий будут рассмотрены в следующих номерах журнала.
Поделитесь материалом с коллегами и друзьями