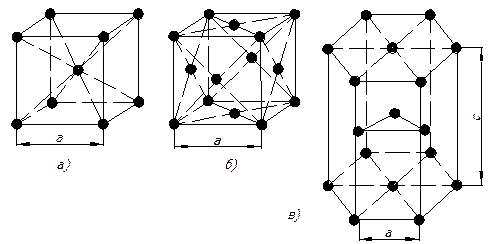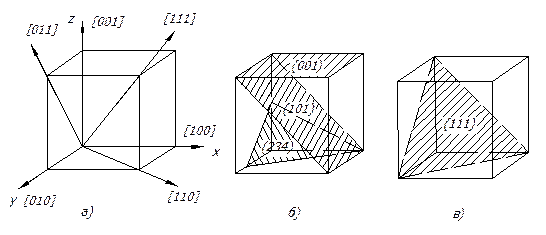Что такое базис решетки
Что такое базис решетки
Одним из основных представлений, связанных со структурой кристаллов, является понятие об элементарной ячейке. В общем случае элементарную ячейку можно представить, как минимальный объём кристалла, параллельные переносы (трансляции) которого в трёх измерениях позволяют построить всю кристаллическую решётку.
Закономерности строения элементарной ячейки, в частности степень их симметричности определяет многие свойства кристалла, в первую очередь электрические, магнитные и механические. Элементарная ячейка может содержать как один, так и несколько атомов. Так у многих металлов, например железа, хрома, меди, серебра, она состоит из одного атома. В тех случаях когда, кристалл состоит из нескольких химических элементов, например, натрия и хлора, элементарная ячейка будет содержать два атома: натрий и хлор. Широко распространены кристаллы с элементарной ячейкой, состоящей из нескольких сцепленных друг с другом молекулярных групп, например кристаллы льда или же многих магнитных материалов. Существуют кристаллы, например, белковые, элементарная ячейка которых состоит из молекул, содержащих несколько тысяч атомов.
Каждый узел, находящийся в вершине элементарной ячейки, принадлежит еще восьми соседним элементарным ячейкам. Поскольку всего узлов (или вершин параллелепипеда) восемь, то ( 
) и на примитивную элементарную ячейку приходится всего один узел.
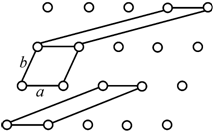
Казалось бы, что выбор элементарной ячейки произволен. На рис. 1.6 все три плоские ячейки примитивны. Хотя трансляции в двух из них и не являются кратчайшими, но любая из них воспроизводит при переносе параллельно самой себе в двух направлениях всю «структуру кристалла». Однако Бравэ были сформулированы 3 правила выбора элементарных ячеек, выполняемые в указанной ниже последовательности.
1. Симметрия элементарной ячейки должна соответствовать симметрии кристалла.
2. Элементарная ячейка должна иметь максимальное число равных ребер и равных углов.
3. При условии выполнения двух первых правил элементарная ячейка должна иметь минимальный объем.
При выполнении этих правил элементарная ячейка, в отличие от примитивной, кроме узлов в вершинах, может иметь дополнительные узлы.
Рис. 1.5. Элементарная ячейка
Рис. 1.6. Различные способы выбора элементарных ячеек
Совокупность координат всех узлов, приходящихся на элементарную ячейку, часто называют ее базисом. Сложную ячейку обычно выбирают так, чтобы узлы находились либо в центрах граней, либо в центре объема. Поэтому принята система наиболее распространенных видов сложных ячеек.
Приведем примеры сложных элементарных ячеек в узлах которых находятся атомы одного сорта.
Параметры решетки, базис, координационное число
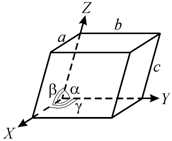
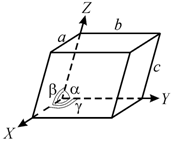
В общем случае элементарная ячейка кристаллической решетки представляет собой наклонный параллелепипед (рис. 8).
Если поместить начало координат в одну из вершин ячейки, то расстояния а,b,c до ближайших вершин и углы a, b, g между координатными осями называют параметрами кристаллической решетки.
Базис решетки- это число атомов, приходящихся на однуэлементарную ячейку.
В гексагональной плотноупакованной ячейке 17 атомов. На ГПУ ячейку
Кристаллическая решетка характеризуется также координационным числом К, которое показывает число атомов, расположенных на ближайшем одинаковом расстоянии от любого атома. Для ОЦК решетки К = 8, для ГЦК и ГПУ решеток К = 12. Чем выше координационное число, тем большая плотность упаковки атомов в ячейке.
1.4 Плотность упаковки атомов в решетке
При моделировании кристаллической решетки в виде соприкасающихся шаровмежду ними образуются пустоты.
Индексация плоскостей и направлений
В кристаллической решетке
Индексация плоскостей
Для обозначения плоскостей и направлений в кристаллической решетке используют индексы, связанные с координатными осями [3].
Положение плоскости определяется отрезками, отсекаемыми ею на координатных осях. За единицу измерения вдоль каждой оси принимают параметр ( период ) решетки в направлении данной оси. Чтобы не иметь дело с бесконечностями, а также дробными числами, используют величины, обратные отрезкам, отсекаемым плоскостью на координатных осях, причем отношение
этих величин приводят к отношению трех наименьших целых чисел. Совокупность таких чисел ( h,k,l ), заключенная в круглые скобки, называется индексами Миллера.
Индексы плоскости отыскиваются следующим образом. Определяются отрезки А, В и С, которые этой плоскостью отсекаются на осях координат.
Записываются величины, обратные отсекаемым отрезкам, например: 1/А, 1/В,1/С. Полученные дроби приводят к общему знаменателю, например,
это будет число D. Целые числа h = D / А, k = D / В, l = D / С и являются индексами данной плоскости.
Определим, например, индексы плоскости, которая отсекает на осях координат отрезки А = 
, В = 2 и С = 
. Отношения 
: 
: 
=
= 
. Общий знаменатель D = 2.
плоскости являются величины h = 
, k = 
, l = 
.
Обозначение плоскости (416).
Примеры индексации плоскостей в кубической решетке показаны на рис. 10, а
в гексагональной плотноупакованной решетке – на рис. 11.
Непараллельные плоскости, имеющие одинаковое атомное строение (количество атомов и их расположение), кристаллографически эквивалентны.
Всю совокупность эквивалентных плоскостей обозначают индексом какой-либо одной плоскости, заключенным в фигурные скобки. Например, плоскости 100, 010, 001, 100, 010, 001. Их обозначают индексом одной какой-либо плоскости и заключают в фигурные скобки как семейство плоскостей <100>или <001>. Другой пример, семейство <111>. Это плоскости 111, 111,111, 111 и др. Если плоскость проходит через начало координат, то для удобства ее
индексации начало координат следует перенести в какую-либо соседнюю вершину элементарной ячейки.
Индексация направлений
Ориентация прямой определяется координатами двух ее точек. Если выбрать из семейства прямых ту, которая проходит через начало координат, или перенести прямую параллельно самой себе так, чтобы она прошла через
начало координат, то направление прямой определится координатами только второй ее точки.
Примеры обозначения направлений в кубической и гексагональной плотноупакованной ( ГПУ) решетке показаны на рис. 12 и 13.
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).
Что такое базис решетки
Одним из основных представлений, связанных со структурой кристаллов, является понятие об элементарной ячейке. В общем случае элементарную ячейку можно представить, как минимальный объём кристалла, параллельные переносы (трансляции) которого в трёх измерениях позволяют построить всю кристаллическую решётку.
Закономерности строения элементарной ячейки, в частности степень их симметричности определяет многие свойства кристалла, в первую очередь электрические, магнитные и механические. Элементарная ячейка может содержать как один, так и несколько атомов. Так у многих металлов, например железа, хрома, меди, серебра, она состоит из одного атома. В тех случаях когда, кристалл состоит из нескольких химических элементов, например, натрия и хлора, элементарная ячейка будет содержать два атома: натрий и хлор. Широко распространены кристаллы с элементарной ячейкой, состоящей из нескольких сцепленных друг с другом молекулярных групп, например кристаллы льда или же многих магнитных материалов. Существуют кристаллы, например, белковые, элементарная ячейка которых состоит из молекул, содержащих несколько тысяч атомов.
Каждый узел, находящийся в вершине элементарной ячейки, принадлежит еще восьми соседним элементарным ячейкам. Поскольку всего узлов (или вершин параллелепипеда) восемь, то ( 
) и на примитивную элементарную ячейку приходится всего один узел.
Казалось бы, что выбор элементарной ячейки произволен. На рис. 1.6 все три плоские ячейки примитивны. Хотя трансляции в двух из них и не являются кратчайшими, но любая из них воспроизводит при переносе параллельно самой себе в двух направлениях всю «структуру кристалла». Однако Бравэ были сформулированы 3 правила выбора элементарных ячеек, выполняемые в указанной ниже последовательности.
1. Симметрия элементарной ячейки должна соответствовать симметрии кристалла.
2. Элементарная ячейка должна иметь максимальное число равных ребер и равных углов.
3. При условии выполнения двух первых правил элементарная ячейка должна иметь минимальный объем.
При выполнении этих правил элементарная ячейка, в отличие от примитивной, кроме узлов в вершинах, может иметь дополнительные узлы.
Рис. 1.5. Элементарная ячейка
Рис. 1.6. Различные способы выбора элементарных ячеек
Совокупность координат всех узлов, приходящихся на элементарную ячейку, часто называют ее базисом. Сложную ячейку обычно выбирают так, чтобы узлы находились либо в центрах граней, либо в центре объема. Поэтому принята система наиболее распространенных видов сложных ячеек.
Приведем примеры сложных элементарных ячеек в узлах которых находятся атомы одного сорта.
Элементарная ячейка. Базис решетки
Одним из основных представлений, связанных со структурой кристаллов, является понятие об элементарной ячейке. В общем случае элементарную ячейку можно представить, как минимальный объём кристалла, параллельные переносы (трансляции) которого в трёх измерениях позволяют построить всю кристаллическую решётку.
Закономерности строения элементарной ячейки, в частности степень их симметричности определяет многие свойства кристалла, в первую очередь электрические, магнитные и механические. Элементарная ячейка может содержать как один, так и несколько атомов. Так у многих металлов, например железа, хрома, меди, серебра, она состоит из одного атома. В тех случаях когда, кристалл состоит из нескольких химических элементов, например, натрия и хлора, элементарная ячейка будет содержать два атома: натрий и хлор. Широко распространены кристаллы с элементарной ячейкой, состоящей из нескольких сцепленных друг с другом молекулярных групп, например кристаллы льда или же многих магнитных материалов. Существуют кристаллы, например, белковые, элементарная ячейка которых состоит из молекул, содержащих несколько тысяч атомов.
Каждый узел, находящийся в вершине элементарной ячейки, принадлежит еще восьми соседним элементарным ячейкам. Поскольку всего узлов (или вершин параллелепипеда) восемь, то ( 
) и на примитивную элементарную ячейку приходится всего один узел.
Казалось бы, что выбор элементарной ячейки произволен. На рис. 1.6 все три плоские ячейки примитивны. Хотя трансляции в двух из них и не являются кратчайшими, но любая из них воспроизводит при переносе параллельно самой себе в двух направлениях всю «структуру кристалла». Однако Бравэ были сформулированы 3 правила выбора элементарных ячеек, выполняемые в указанной ниже последовательности.
1. Симметрия элементарной ячейки должна соответствовать симметрии кристалла.
2. Элементарная ячейка должна иметь максимальное число равных ребер и равных углов.
3. При условии выполнения двух первых правил элементарная ячейка должна иметь минимальный объем.
При выполнении этих правил элементарная ячейка, в отличие от примитивной, кроме узлов в вершинах, может иметь дополнительные узлы.
 |  |
| Рис. 1.5. Элементарная ячейка | Рис. 1.6. Различные способы выбора элементарных ячеек |
Совокупность координат всех узлов, приходящихся на элементарную ячейку, часто называют ее базисом. Сложную ячейку обычно выбирают так, чтобы узлы находились либо в центрах граней, либо в центре объема. Поэтому принята система наиболее распространенных видов сложных ячеек.
Приведем примеры сложных элементарных ячеек в узлах которых находятся атомы одного сорта.
Объемноцентрированная ячейка (обозначается буквой I) (рис. 1.7, a). Кроме узла, находящегося в начале координат, она имеет дополнительный узел, расположенный на пересечении телесных диагоналей. Таким образом, на данную элементарную ячейку приходится всего два узла и ее базис [[000]], [[½ ½ ½]].
Базоцентрированная ячейка (обозначается буквой С)(рис. 1.7, б), так же как и объемноцентрированная, характеризуется базисом из двух узлов, индексы которых [[000]], [[½ ½ 0]]. На рисунке видно, что в этой ячейке дополнительные узлы находятся в центрах граней, перпендикулярных оси c. Ясно, что данные узлы принадлежат этой ячейке только наполовину, но т. к. таких граней в ячейке две, то ей принадлежит один узел, находящийся на грани.
Бокоцентрированная ячейка. Возможны два варианта: А-ячейка, в которой центрирована грань, перпендикулярная оси а, и В—ячейка, где дополнительные узлы находятся в центре граней, перпендикулярных оси b, базисы которых соответственно: А − [[000]], [[0 ½ ½]] (рис. 1.7, г), B − [[000]], [[½ 0 ½]] (рис. 1.7, в).
Гранецентрированная ячейка (рис. 1.7, д) (обозначается буквой F). Дополнительные узлы находятся в центрах граней. Общее число узлов, приходящихся на гранецентрированную ячейку, четыре. Ее базис [[000]], [[0 ½ ½]], [[½ 0 ½]], [[½ ½ 0]].
Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)
Кристаллическое строение металлов
Закономерное расположение атомов в кристалле описывается кристаллической решеткой, т.е. трехмерным, периодически повторяющимся расположением атомов во всем объеме кристалла. Наименьший объем, который характеризует особенности строения кристалла данного металла, называется элементарной ячейкой. Последовательные перемещения элементарной ячейки на определенные расстояния, называемые трансляциями решетки, позволяют последовательно пройти все области кристалла. Ячейки, или кристаллические решетки характеризуются следующими основными параметрами: симметрией, периодами решетки, координационными числами и коэффициентами компактности решетки.
Большинство металлов кристаллизуется в трех типах решеток: гранецентрированной кубической, объемно-центрированной кубической и гексагональной, которая может быть плотноупакованной и неплотноупакованной. Эти три типа решеток приведены на рис. 2.
У большинства металлов периоды решеток находятся в пределах от 0,25 до 0,55 нм.
Рис. 2. Элементарные ячейки плотноупакованных кристаллических решеток:
Коэффициент компактности решеткиh определяется отношением объема, занимаемого атомами с условно сферической формой Va, ко всему объему ячейки Vp, т.е.
Для ОЦК решеток коэффициент компактности равен 0,68, для ГЦК и для ГПУ решеток он равен 0,74 (при с/а = 1,633).
При решении задач, стоящих перед металлографией, необходимо иметь систему обозначений для записи ориентации граней кристалла и плоскостей, расположенных внутри кристалла.
Чтобы определить индексы Миллера необходимо выполнить следующие действия: найти отрезки, отсекаемые плоскостью на осях координат, измеренные в осевых единицах (периодах решетки), взять обратные значения этих чисел и привести эти значения к целым числам. Например, рассматриваемая плоскость (рис. 3, б) отсекает на оси Х отрезок равный 1, на оси Y — равный 2/3, на оси Z—1/2 периодов трансляций. Тогда отрезки, обратные указанным, будут равны 1, 3/2 и 2. После приведения этих дробей к общему знаменателю получим числители равные индексам данной плоскости, т.е. h = 2, k = 3, l = 4. Полученные числа записывают в указанном порядке и заключают в круглые скобки: (234).
Рис. 3. Кристаллографические индексы направлений (а)
и плоскостей (б, в) в кубических решетках
При индицировании направлений, одну точку прямой помещают в начало координат, а другую получают путем последовательного векторного сложения 3-х перемещений, параллельных трем осям координат. Например, точка на прямой, проходящей через начало координат, смещается на Н осевых единиц вдоль оси X, К осевых единиц вдоль оси Y и L единиц вдоль оси Z.
Тогда, если Н, К, и L — три взаимно простых числа, то они являются индексами направления.
При этом важно отметить, чти при определении индексов направлений не нужно пользоваться обратными значениями длин отрезков, отсекаемых на осях координат. В отличие от индексов плоскостей, индексы направлений принято заключать в квадратные скобки, например, [121] или [130]. Индексы наиболее часто встречающихся плоскостей и направлений для кубических решеток приведены на рис. 3.
Одним из наиболее распространенных и прямых методов определения типа кристаллических решеток и размеров элементарных ячеек является метод рентгеноструктурного анализа. Возможно также определение этих величин с помощью дифракции электронов и нейтронов.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет