Что такое базис в астрономии
Измерение расстояний
Вселенная так велика, что привычные на Земле единицы длины, например километр (км), неудобны для измерения космических расстояний. Для масштабов Земли вполне подходят километры, но когда мы говорим, что до ближайшей к нам галактики в созвездии Андромеды 14,4 квинтиллиона км — 14 400 000 000 000 000 000 км, — то число оказывается настолько большим, что становится бесполезным. Поэтому в километрах обычно выражают лишь размеры планет и в отдельных случаях — расстояния в пределах Солнечной системы. Полезной мерой длины для нашей Солнечной системы является астрономическая единица (а. е.) — среднее расстояние от Земли до Солнца, равное 149 597 870,610 км. Так, расстояние от Меркурия до Солнца равно 1/3 а. е., а среднее расстояние от Плутона до Солнца — 40 а. е.
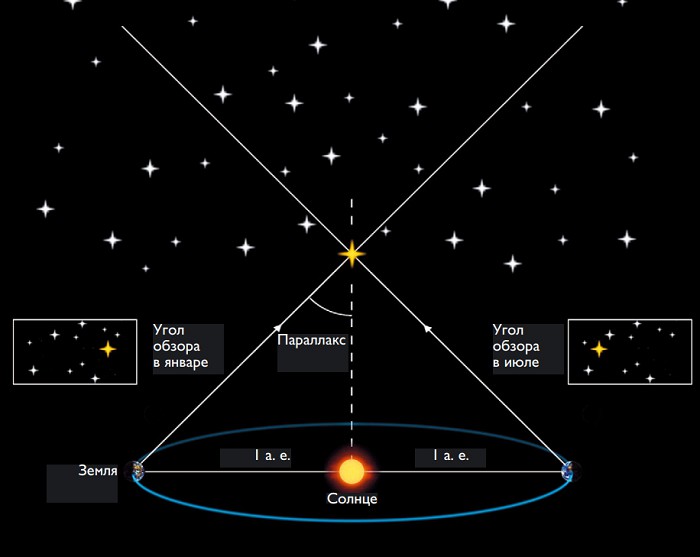
Расстояние до далеких и недоступных нам звезд можно определить из геометрии, измерив направления на этот предмет с двух концов известного отрезка (базиса), а затем рассчитав размеры треугольника, образованного концами отрезка и удаленным предметом. В качестве базиса используется расстояние между двумя точками земной орбиты, которые наша планета проходит с интервалом в несколько месяцев. При перемещении Земли направление на звезду изменится, она немного сместится на фоне более далеких звезд. Такое смещение более близкой звезды на фоне более далеких называется параллаксом.
Существуют и другие методы, с помощью которых расстояние до звезды можно получить косвенным путем, используя различные астрофизические или статистические соотношения.
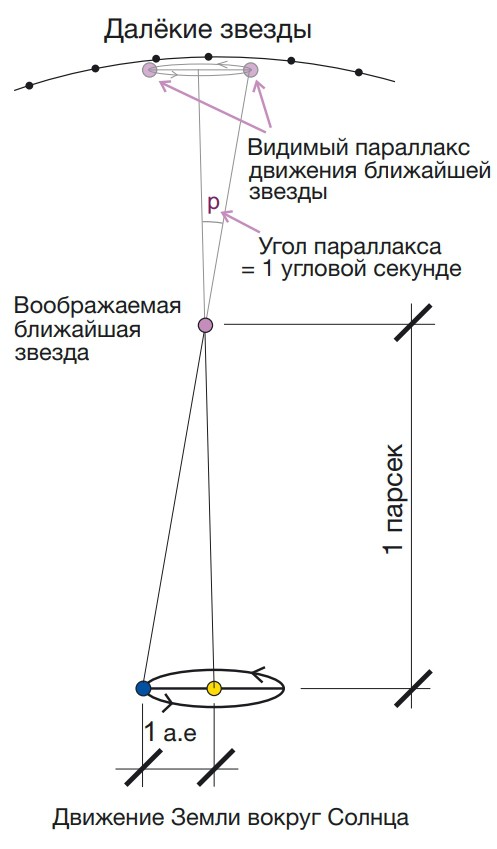
Астрономы, изучающие небесные тела и астрономические объекты, находящиеся за пределами Солнечной системы, в качестве единицы расстояний в своей работе используют парсек (пк) — внесистемную единицу расстояний в астрономии, равную расстоянию до космического объекта, с которого радиус орбиты Земли виден под углом 1”. Средний радиус земной орбиты 149 597 870 690м, и парсек, основанный на орбите Земли, равен 30 856 775 813 057 300 м.
Небесное тело, расположенное на расстоянии всего в один парсек, как раз и имеет годичный параллакс в одну угловую секунду (1/1800 диаметра Луны, который приблизительно равен 3476 км).
В научно-популярной литературе обычно используется другая внесистемная единица измерения астрономических расстояний — световой год. Световым годом называется расстояние, которое свет (электромагнитные волны) проходит в вакууме за один т. н. юлианский год, состоящий из 365,25 дней по 86 400 секунд каждый. Скорость света составляет 299 792 км в секунду, и ничто во Вселенной не движется быстрее. Двигаясь со скоростью около 300 000 км в секунду, свет может семь раз обогнуть Землю буквально за одно мгновение. Один световой год приблизительно равен 9,46 триллионов километров (9,46 · 10 12 км).
1 парсек ≈ 3,26 св. года ≈ 206 000 а. е.
Ближайшая к нашей Солнечной системе звезда Проксима Центавра (Кентавра) удалена от нас на расстояние 4,2 световых года (для сравнения, свет Солнца достигает Земли за 8,5 минут, то есть мы всегда видим то, что происходило на Солнце 8,5 минут ранее). Проксима Центавра — это светило, которое в 7 раз меньше Солнца и довольно тусклое, мы видим его лишь потому, что оно расположено очень близко от нас. Более яркие объекты мы сможем увидеть с более далекого расстояния.
Например, гораздо ярче звезд гигантские звездные системы — галактики. Одна из наших ближайших соседок по космосу, галактика Андромеды, удалена от нас на 2,5 млн световых лет. Одной из самых далеких звездных систем в настоящее время является галактика EGS8p7. Ее свету понадобилось 13,24 млрд лет, чтобы долететь до Земли. Мы видим эту галактику лишь потому, что на луче зрения в направлении нее практически отсутствует нейтральный газ, хорошо поглощающий свет. С улучшением астрономических методов и приборов мы будем заглядывать все дальше и дальше вглубь Вселенной, так что EGS8p7 не самая далекая звездная система, которую разглядит человечество.
Чтобы оценить масштабы расстояний в космосе (и то, почему для их измерений используется столько различных единиц), сравним расстояния от Земли до разных объектов:
Урок 10
Для измерения расстояний в пределах Солнечной системы используют астрономическую единицу (а. е.), которая равна среднему расстоянию от Земли до Солнца.
1 а.е. = 149 600 000 км
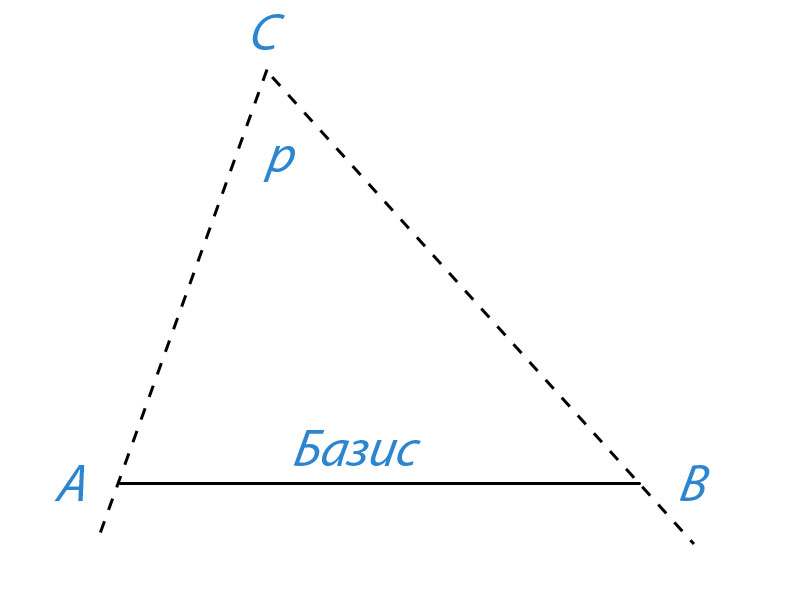
Параллакс — угол p, под которым из недоступного места (точка C) будет виден отрезок AB, называемый базисом.
Базис — тщательно измеренное расстояние от точки A (наблюдатель) до какой-либо достигнутой для наблюдения точки B.
По величине базиса и прилегающим к нему углам треугольника ABC найти расстояние AC. При измерениях на Земле этот метод называют триангуляцией.
r = D · sin(ρ); R = D · sin(ρ)/sin(p) · R; r = ρ/p · R.
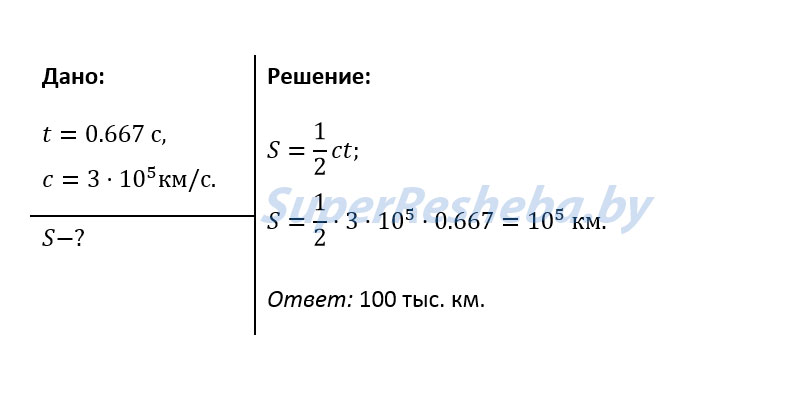
1. Радиолокатор зафиксировал отраженный сигнал от пролетающего вблизи Земли астероида через t — 0,667 с. На каком расстоянии от Земли находился в это время астероид?
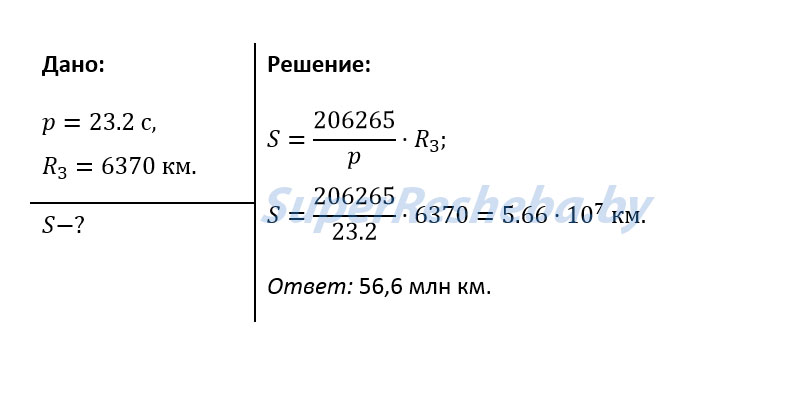
2. Определите расстояние от Земли до Марса во время великого противостояния, когда его горизонтальный параллакс p = 23,2″.
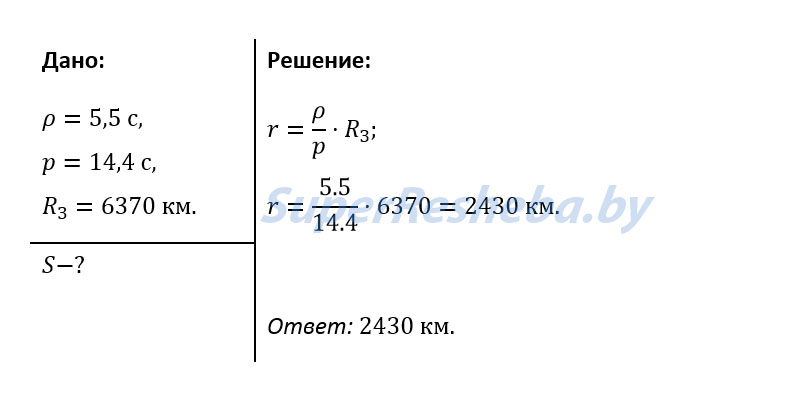
3. При наблюдении прохождения Меркурия по диску Солнца определили, что его угловой радиус p = 5,5″, а горизонтальный параллакс p = 14,4″. Определите линейный радиус Меркурия.
1. Сигнал, посланный радиолокатором к Венере, возвратился назад через t — 4 мин 36 с. На каком расстоянии в это время находилась Венера в своем нижнем соединении?
2. На какое расстояние к Земле подлетал астероид Икар, если его горизонтальный параллакс в это время был p = 18,0″?
3. С помощью наблюдений определили, что угловой радиус Марса p = 9,0″, а горизонтальный параллакс p = 16,9″. Определите линейный радиус Марса.
Как измеряют расстояния до удалённых астрономических объектов?
Нередко в научно-популярных статьях по астрономии мы читаем, что расстояние до того или иного космического объекта, о котором идёт речь, составляет тысячи, миллионы или даже миллиарды световых лет. Как же удалось измерить столь колоссальные расстояния? Об этом мы и поговорим сегодня.
Наиболее давним методом измерения расстояний до удалённых объектов является так называемый метод параллактического смещения. Он работает не только в космосе, но и на Земле.
Предположим, к примеру, что вам надо измерить расстояние до дерева, находящегося на другом берегу реки. Для того, чтобы сделать это, не переплывая реку с рулеткой в руках, можно проделать следующую процедуру: выбрать некий отрезок (его ещё называют базисом), длина которого строго известна, а затем измерить углы, которые образуются между базисом и направлением на объект в противоположных концах базиса.
Зная длину базиса (СВ) и углы АСВ и СВА можно без труда решить данный треугольник и найти длину отрезка АС (или АВ), определив таким образом расстояние до объекта.
Разумеется, чем больше расстояние до объекта, тем больший базис нам нужно выбрать. Поэтому для измерения расстояний до космических объектов (даже ближайших) нужно выбирать достаточно значительные. Например, расстояния вроде диаметра Земли, а ещё лучше диаметра орбиты Земли вокруг Солнца. Если замерить угол, под которым видна, скажем, звезда из одной и той же точки в некий момент времени, а затем повторить измерение ровно через полгода, то можно посчитать параллактическое смещение именно с таким базисом.
Таким образом астрономам удалось определить расстояние до многих звёзд Млечного Пути; однако для более удалённых объектов, вроде иных галактик (даже ближайших) этот метод уже не работает: параллактическое смещение оказывается слишком незначительным.
Для измерения расстояния до таких объектов используется так называемый закон Хаббла. Чтобы понять, что это такое и как оно работает, нам нужно отклониться немного в сторону.
Как известно, Вселенная расширяется. Однако её расширение многие представляют неверно. Не слишком сведующим в современной космологии представляется, что расширение Вселенной происходит подобно тому, как разлетаются в разные стороны осколки взорвавшейся гранаты. Но это не так. Фактически, можно сказать, что ничто во Вселенной никуда не разлетается: просто пространство между объектами как бы «разбухает»: 1 световой год через некоторое время превращается в 1,1 световых года.
Разумеется, значимое влияние этот закон оказывает лишь на больших (космических)
Но для того, чтобы по скорости определить расстояние по закону Хаббла, нужно знать ещё постоянную Хаббла, то есть, коэффициент пропорциональности между скоростью объекта и расстоянием до него.
И когда телескопы стали достаточно мощны для того, чтобы различить отдельные звёзды в других галактиках, а затем и для того, чтобы выделить среди них цефеиды и посчитать расстояние до них, стало возможным определить и расстояние до этих галактик. Ну а зная его, мы смогли определить значение постоянной Хаббла
Именно закон Хаббла и красное смещение являются наиболее актуальными методами измерения расстояний до удалённых объектов во Вселенной.
Астрономический базис
Основные модели времени, на которых основаны мои продукты в рамках проекта Лин Ци, оформились в процессе многолетней работы над «астрологическим» калькулятором qmdj.biz.
Почему «астрология», применительно к qmdj.biz, взята в кавычки я расскажу в других публикациях, посвящённых непосредственно системе Цимэнь Дуньцзя. А здесь речь пойдёт об астрономии.
В основном блоке китайских наук о времени важную роль играют солнцестояния, равноденствия, годовой цикл солнца и его деления: два полугодия (ян дунь и инь дунь), 24 солнечных сезона, — все эти периоды представляют собой просто разделение годового цикла на части. Наиболее очевидным способом деления было бы взять 365.2461592616864 суток года и разделить на соответствующее число частей. Но в системе китайского календаря за основу берётся не временнáя длительность года, а 360 градусов годового движения Солнца вокруг Земли (эклиптики). Или Земли вокруг Солнца, что в данном случае не существенно, потому что механика всей остальной солнечной системы нас не интересует. Далее эти 360 градусов делятся на равные сектора. Так один месяц в китайской календарной системе — это 30 градусов эклиптики. Поскольку Земля вокруг Солнца движется с неодинаковой в течение года угловой скоростью, то некоторые 30-градусные сектора пролетаются планетой чуть быстрее, а некоторые чуть медленнее.
Таким образом, чтобы определить, в какой момент времени наступает смена месяца, нужно определить, в какой момент времени Земля пересекает очередное 30-градусное деление.
На графике изображена зависимость градуса положения Земли от времени. Истинная кривая очень мало отличается от прямой, поэтому для наглядности приводим и утрированную зависимость.
Тут можно заметить, что летом угловое движение земли замедляется. Изо дня в день градус положения нарастает медленно. А зимой, наоборот, угловая скорость повышается. Выходит, что летние месяцы немного дольше, 30 градусов преодолеваются за больше времени. А зимние месяцы короче, зимой 30 градусов преодолеваются за более короткое время.
В наших приложениях, чтобы определить момент времени, когда происходит смена китайского месяца, необходимо найти точку на оси времени, когда этот график доходит до очередного 30-градусного уровня. По сути это требует решения нелинейного уравнения.
Другая нелинейность в календарной системе связана с сутками и часами. В течение суток солнце то поднимается над горизонтом — это день, — то опускается под горизонт — это ночь. Сутки длятся с момента, когда солнце достигает самой низкой точки под горизонтом до следующего такого момента. Этот момент называют астрономической полночью.
Нам известно, что сутки длятся ровно 24 часа. Но на самом деле длительность суток меняется в течение года. 24 часа — это усреднённая длительность суток. Иногда от полуночи до полуночи проходит больше времени, иногда меньше. Земля делает полный суточный оборот то быстрее, то медленнее.
Вслед за переменчивой длительностью суток мы можем ввести переменную длительность часов, минут, секунд, так чтобы в сутках всё равно оставалось ровно 24 часа, но только часы эти будут иметь плавающую длительность в течение года. Таким образом мы получим по сути то же самое время, которое наши предки наблюдали на солнечных часах. Они не задумывались об эталонной секунде по атомному стандарту, не полагались на электронику. Они просто брали реальную длительность суток по солнцу и делили её на части, чтобы получить часы, минуты, секунды. В июне и особенно в декабре они оказывались чуть дольше, а в марте и сентябре чуть короче.
В приложениях Лин Ци мы работаем именно с природным временем, какое показывали бы солнечные часы. Но поскольку все бытовые и компьютерные системы показывают нам усреднённое равномерное эталонное время, нам приходится пересчитывать эталонное время на переменное природное. Получается, что это природное время, или как его называют «наблюдаемое» (apparent time), то опережает наше равномерное, то отстаёт от него.
Это явление известно как «Уравнение времени».
В китайской календарной модели сутки содержат 12 «китайских часов», каждый из которых равен двум нашим часам. Суточный круг подъёма и спуска солнца между астрономическими полуднем и полуночью мы делим на 12 частей. Каждая часть равна точно 120 минутам природного времени, но эта длительность в эталонном времени меняется в течение года.
Так мы сталкиваемся с задачей, похожей на задачу о границах месяцев. Чтобы выяснить, в какой момент по нашим усреднённым часам наступает смена китайского часа или смена суток, нам вновь нужно решать нелинейное уравнение.
Все эти соображения имеют исключительно астрономический характер. В них нет ничего специфически китайского. Эталонное время и отклонение природного времени от эталонного — это проблематика XX века, возникшая в результате повсеместной стандартизации, а затем компьютеризации часов. Соображения же о неравномерном движении Земли вокруг Солнца известны давно. И в самой китайской научной мысли в течение веков снова и снова предпринимались попытки уточнения расчётов. Эти уточнения не были достоянием исключительно китайской мысли. Заметное влияние и помощь оказывали индийские буддийские монахи, мусульманские астрономы, иезуитские учёные.
В наших расчётах мы опираемся на высокоточные астрономические модели, учитывающие прецессию, нутацию земной оси, вековую аберрацию, исторически зафиксированные сбои в движении Земли в результате катаклизмов.
1. Закончите предложения.
Для измерения расстояний в пределах Солнечной системы используют астрономическую единицу (а. е.), которая равна среднему расстоянию от Земли до Солнца.
1 а.е. = 149 600 000 км
2. Дайте определения понятиям «параллакс» и «базис»; на рисунке 10.1 покажите эти величины.
Параллакс — угол p, под которым из недоступного места (точка C) будет виден отрезок AB, называемый базисом.
Базис — тщательно измеренное расстояние от точки A (наблюдатель) до какой-либо достигнутой для наблюдения точки B.
3. Как с помощью понятий параллакса и базиса определить расстояние до удаленного недоступного объекта С (рис. 10.1)?
По величине базиса и прилегающим к нему углам треугольника ABC найти расстояние AC. При измерениях на Земле этот метод называют триангуляцией.
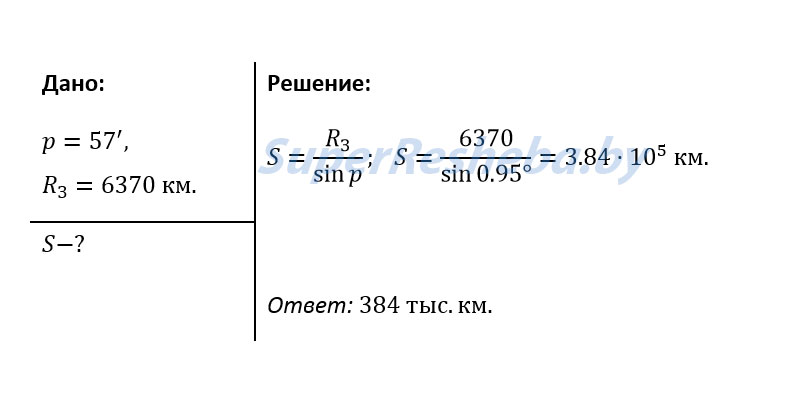
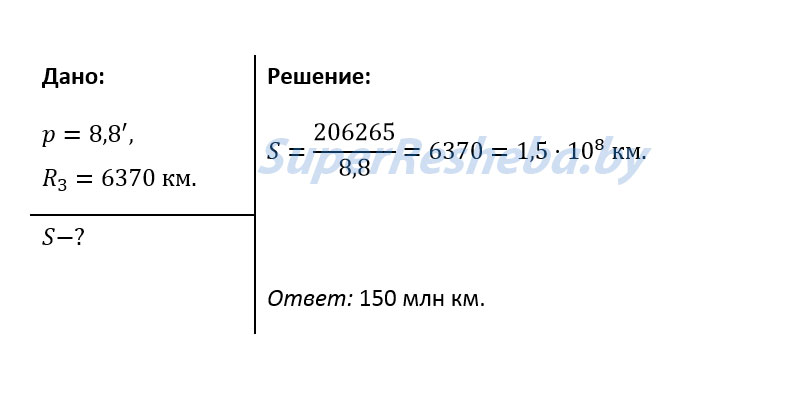
4. Угол, под которым со светила S виден радиус Земли, перпендикулярный лучу зрения, называется горизонтальным параллаксом p (рис, 10.2). Определите расстояния: а) до Луны, если ее горизонтальный параллакс p = 57′; б) до Солнца, горизонтальный параллакс которого p = 8,8″.
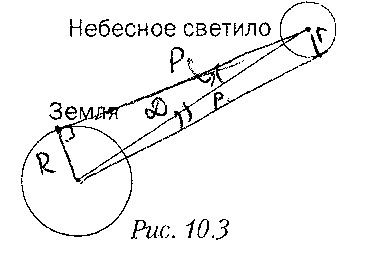
5. Дополните рисунок 10.3 необходимыми построениями и выведите формулу, позволяющую определить радиус небесного светила (в радиусах Земли), если известны угловой радиус светила p и его горизонтальный параллакс p.
r = D · sin(ρ); R = D · sin(ρ)/sin(p) · R; r = ρ»/p» · R.
6. Решите следующие задачи (при расчетах считайте, что c = 3 · 10 5 км/с, R3 = 6370 км).
1. Радиолокатор зафиксировал отраженный сигнал от пролетающего вблизи Земли астероида через t — 0,667 с. На каком расстоянии от Земли находился в это время астероид?
2. Определите расстояние от Земли до Марса во время великого противостояния, когда его горизонтальный параллакс p = 23,2″.
3. При наблюдении прохождения Меркурия по диску Солнца определили, что его угловой радиус p = 5,5″, а горизонтальный параллакс p = 14,4″. Определите линейный радиус Меркурия.
1. Сигнал, посланный радиолокатором к Венере, возвратился назад через t — 4 мин 36 с. На каком расстоянии в это время находилась Венера в своем нижнем соединении?
2. На какое расстояние к Земле подлетал астероид Икар, если его горизонтальный параллакс в это время был p = 18,0″?
3. С помощью наблюдений определили, что угловой радиус Марса p = 9,0″, а горизонтальный параллакс p = 16,9″. Определите линейный радиус Марса.