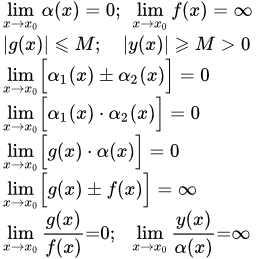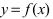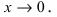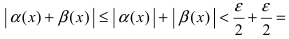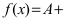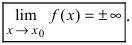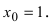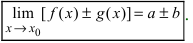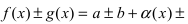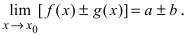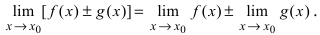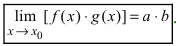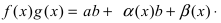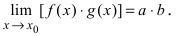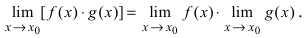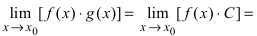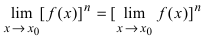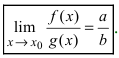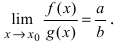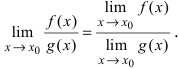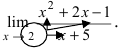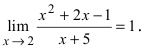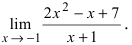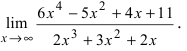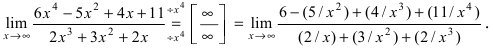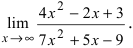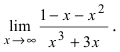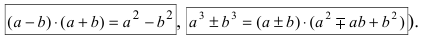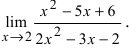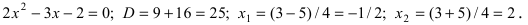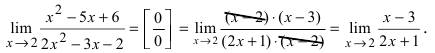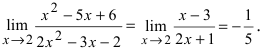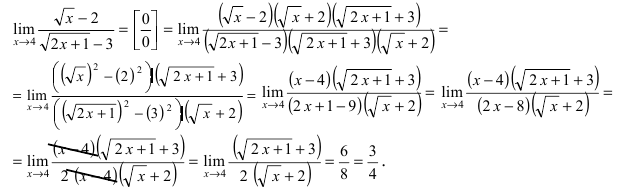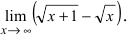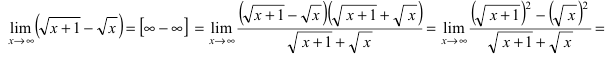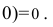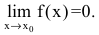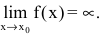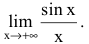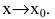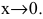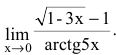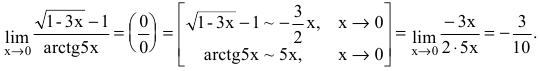Что такое бесконечно большая функция

Примеры

то говорят о положительной или отрицательной б.б. при %%a%% функции.

Пример

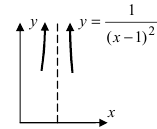
Функция %%1/%% — положительная б.б. при %%x \to 0%%.

Связь между б.б. и б.м. функциями

Если %%f(x)%% — б.б. при %%x \to a%% функция, то %%1/f(x)%% — б.м.

при %%x \to a%%. Если %%\alpha(x)%% — б.м. при %%x \to a%% функция, отличная от нуля в некоторой проколотой окрестности точки %%a%%, то при %%x \to a%%.

Свойства бесконечно больших функций

Приведем несколько свойств б.б. функций. Эти свойства непосредственно следуют из определения б.б. функции и свойств функций, имеющих конечные пределы, а также из теоремы о связи между б.б. и б.м. функциями.

Сумма ограниченной в некоторой проколотой окрестности точки %%a%% функции и б.б. функции при %%x \to a%% есть б.б. функция при %%x \to a%%.

Сумма двух б.б. функций при %%x \to a%% есть неопределенность. В зависимости от знака слагаемых характер изменения такой суммы может быть самым различным.

Пример

Источник

Бесконечно малые и бесконечно большие функции

Определение бесконечно малой и бесконечно большой функции

Свойства бесконечно малых функций

Свойство суммы, разности и произведения бесконечно малых функций

Теорема о произведении ограниченной функции на бесконечно малую

Свойство о представлении функции в виде суммы постоянной и бесконечно малой функции

Свойства бесконечно больших функций

Теорема о сумме ограниченной функции и бесконечно большой

Теорема о произведении ограниченной снизу функции на бесконечно большую

Теорема о частном от деления ограниченной функции на бесконечно большую

Теорема о частном от деления ограниченной снизу функции на бесконечно малую

Свойство неравенств бесконечно больших функций

Это свойство имеет два частных случая.

Связь между бесконечно большими и бесконечно малыми функциями

Из двух предыдущих свойств вытекает связь между бесконечно большими и бесконечно малыми функциями.

Дополнительные формулы, связывающие символы бесконечности, можно найти на странице
«Бесконечно удаленные точки и их свойства».

Арифметические свойства бесконечно больших и бесконечно малых функций

Приведенные выше свойства выполняются, если функция ограничена, а функция ограничена снизу по абсолютной величине положительным числом. При этом эти функции не обязательно должны иметь конечный предел, а могут расходиться. Однако, эти функции будут обладать указанными свойствами, если они имеют соответствующие пределы. Это позволяет сформулировать арифметические свойства бесконечно больших и бесконечно малых функций.

Доказательство свойств и теорем

Теорема о произведении ограниченной функции на бесконечно малую

Для доказательства этой теоремы, мы воспользуемся определением предела функции по Гейне. А также используем свойство бесконечно малых последовательностей, согласно которому произведение ограниченной последовательности на бесконечно малую является бесконечно малой последовательностью.

Воспользуемся тем, что произведение ограниченной последовательности на бесконечно малую есть бесконечно малая последовательность:
.
Тогда, согласно определению предела последовательности по Гейне,
.

Свойство о представлении функции в виде суммы постоянной и бесконечно малой функции

Теорема о сумме ограниченной функции и бесконечно большой

Для доказательства теоремы, мы воспользуемся определением предела функции по Гейне. Также используем свойство бесконечно больших последовательностей, согласно которому сумма или разность ограниченной последовательности и бесконечно большой является бесконечно большой последовательностью.

Поскольку сумма или разность ограниченной последовательности и бесконечно большой является бесконечно большой последовательностью, то
.
Тогда, согласно определению предела последовательности по Гейне,
.

Теорема о произведении ограниченной снизу функции на бесконечно большую

Для доказательства этого свойства, мы воспользуемся определением предела функции по Гейне. Также используем свойство бесконечно больших последовательностей, согласно которому произведение бесконечно большой и ограниченной снизу последовательности является бесконечно большой последовательностью.

Поскольку произведение бесконечно большой и ограниченной снизу последовательности является бесконечно большой последовательностью, то
.
Согласно определению предела последовательности по Гейне,
.

Теорема о частном от деления ограниченной функции на бесконечно большую

Для доказательства, мы воспользуемся определением предела функции по Гейне. Также используем свойство бесконечно больших последовательностей, согласно которому частное от деления ограниченной последовательности на бесконечно большую является бесконечно малой последовательностью.

Поскольку частное от деления ограниченной последовательности на бесконечно большую является бесконечно малой последовательностью, то
.
Тогда, согласно определению предела последовательности по Гейне,
.

Теорема о частном от деления ограниченной снизу функции на бесконечно малую

Для доказательства этого свойства, мы воспользуемся определением предела функции по Гейне. Также используем свойство бесконечно больших последовательностей, согласно которому частное от деления ограниченной снизу последовательности на бесконечно малую является бесконечно большой последовательностью.

Поскольку частное от деления ограниченной снизу последовательности на бесконечно малую является бесконечно большой последовательностью, то
.
Согласно определению предела последовательности по Гейне,
.

Свойство неравенств бесконечно больших функций

Использованная литература:
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.

Источник

Что такое бесконечно большая функция

БЕСКОНЕЧНО МАЛЫЕ ФУНКЦИИ И ИХ ОСНОВНЫЕ СВОЙСТВА

Функция y=f(x) называется бесконечно малой при x→a или при x→∞, если или , т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.

Установим следующее важное соотношение:

Теорема. Если функция y=f(x) представима при x→aв виде суммы постоянного числа b и бесконечно малой величины α(x): f (x)=b+ α(x) то .

Обратно, если , то f (x)=b+α(x), где a(x) – бесконечно малая при x→a.

Можно доказать и обратную теорему.

Доказательство теоремы проведите самостоятельно.

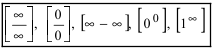
Таким образом, простейшие свойства бесконечно малых и бесконечно больших функций можно записать с помощью следующих условных соотношений: A≠ 0

.

ТЕОРЕМЫ О ПРЕДЕЛАХ

Теорема 1. Предел алгебраической суммы двух, трех и вообще определенного числа функций равен алгебраической сумме пределов этих функций, т.е.

.

Доказательство. Проведем доказательство для двух слагаемых, так как для любого числа слагаемых оно проводится так же. Пусть .Тогда f(x)=b+α(x) и g(x)=c+β(x), где α и β – бесконечно малые функции. Следовательно,

Так как b + cесть постоянная величина, а α(x) + β(x) – функция бесконечно малая, то

.

Пример. .

Теорема 2. Предел произведения двух, трех и вообще конечного числа функций равен произведению пределов этих функций:

.

Доказательство. Пусть . Следовательно, f(x)=b+α(x) и g(x)=c+β(x) и

fg = (b + α)(c + β) = bc + (bβ + cα + αβ).

Произведение bc есть величина постоянная. Функция bβ + c α + αβ на основании свойств бесконечно малых функций есть величина бесконечно малая. Поэтому .

Следствие 1. Постоянный множитель можно выносить за знак предела:

.

Следствие 2. Предел степени равен степени предела:

.

Пример..

Теорема 3. Предел частного двух функций равен частному пределов этих функций, если предел знаменателя отличен от нуля, т.е.

.

Доказательство. Пусть . Следовательно, f(x)=b+α(x) и g(x)=c+β(x), где α, β – бесконечно малые. Рассмотрим частное

.

Дробь является бесконечно малой функцией, так как числитель есть бесконечно малая функция, а знаменатель имеет предел c 2 ≠0.

Теорема 4. Пусть даны три функции f(x), u(x) и v(x), удовлетворяющие неравенствам u(x)≤f(x)≤ v(x). Если функции u(x) и v(x) имеют один и тот же предел при x→a (или x→∞), то и функция f(x) стремится к тому же пределу, т.е. если

, то .

Смысл этой теоремы понятен из рисунка.

Доказательство теоремы 4 можно найти, например, в учебнике: Пискунов Н. С. Дифференциальное и интегральное исчисления, т. 1 – М.: Наука, 1985.

Теорема 5. Если при x→a (или x→∞) функция y=f(x) принимает неотрицательные значения y≥0 и при этом стремится к пределу b, то этот предел не может быть отрицательным: b≥0.

Доказательство. Доказательство проведем методом от противного. Предположим, что b 3 – 6x 2 + 11x– 6, то при делении получим

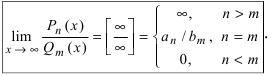
II. Неопределенность .

При вычислении предела числитель и знаменатель данной дроби разделили на x в старшей степени.

При вычислении предела воспользовались равенством ,если x

Источник

Бесконечно малые и бесконечно большие функции с примерами решения

Содержание:

Бесконечно малые и бесконечно большие функции

Бесконечно малые функции и их свойства

Определение: Функция

Пример:

— бесконечно малая функция при — бесконечно малая функция при

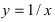
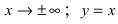
Решение:

Рассмотрим свойства бесконечно малых функций:

1. Сумма (разность) конечного числа бесконечно малых функций есть бесконечно малая функция.

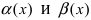
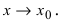
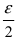
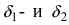
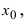
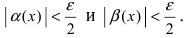
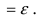
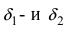
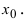
Доказательство: Пусть две бесконечно малые функции при Это означает, что для любого сколь угодно малого положительного числа найдутся такие -окрестности точки что будут выполняться неравенства Следовательно,

Полученное неравенство справедливо в меньшей из -окрестности точки Кроме того, полученное неравенство свидетельствует о том, сумма двух бесконечно малых функций есть бесконечно малая функция.

Замечание: Используя метод математической индукции можно доказать утверждение свойства 1. для любого конечного числа n слагаемых бесконечно малых функций.

Пример:

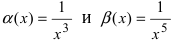
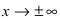
Является сумма бесконечно малых функций при бесконечно малой функцией.

Решение:

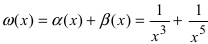
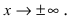
Да, является, так как стремится к нулю при Нижеприведенные свойства бесконечно малых функций приведем без доказательства, так как они доказываются аналогично свойству 1.

2. Произведение бесконечно малых фу нкций есть бесконечно малая функция.

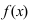
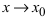
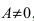
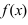
3. Если функция имеет при конечный предел , частное отделения бесконечно малой функции на функцию есть бесконечно малая функция.

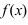
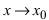
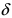
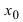
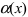
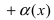
4. Если функция имеет при конечный предел A, то в некоторой -окрестности точки ее можно представить в виде суммы предельного значения А и бесконечно малой в этой окрестности функции , т.е.

.

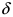
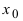
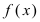
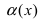
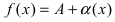
5. (обратное к 4.). Если в некоторой -окрестности точки фу нкцию можно представить в виде суммы предельного значения А и бесконечно малой в этой окрестности функции ,т.е. , то число А является пределом данной функции.

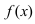
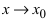
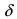
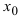
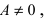
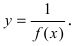
Замечание: Если функция имеет при конечный предел А, то в некоторой -окрестности точки она ограничена. Если то в той же окрестности будет ограничена и функция 6. Произведение бесконечно малой функции на ограниченную функцию есть бесконечно малая функция.

7. Отношение бесконечно малой функции к ограниченной функции есть бесконечно малая функция.

Бесконечно большие функции

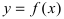
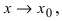
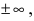
Определение: Функция называется бесконечно большой при если ее предел при этом равен т.е.

Пример:

— бесконечно большая функция при Построим график этой функции в некоторой окрестности точки (Рис. 60):

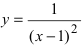
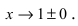
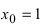
Решение:

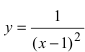
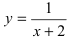
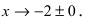
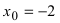
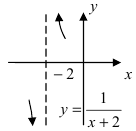
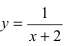
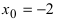
График функции у = в малой окрестности точки

— бесконечно большая функция при Покажем поведение этой функции в некоторой окрестности точки (Рис. 61):

Рис. 61. График функции в малой окрестности точки . Рассмотрим свойства бесконечно больших функций:

1. Сумма бесконечно больших при 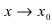функций есть бесконечно большая функция.

Замечание: При вычислении разности бесконечно больших функций может получиться любое вещественное число.

2. Произведение бесконечно больших функций есть бесконечно большая функция.

Замечание: При вычислении отношения бесконечно больших функций может получиться любое вещественное число.

3. Произведение бесконечно большой функции на ограниченную функцию есть бесконечно большая функция.

35. Вычисление произведения бесконечно большой функции на бесконечно малую функцию может привести к любому вещественному числу.

4. Отношение бесконечно большой функции к ограниченной функции есть бесконечно большая функция.

Установим связь между бесконечно большими и бесконечно малыми функциями, которая дается следующими теоремами:

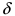
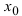
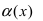
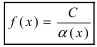
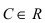
Теорема: Если в некоторой -окрестности точки функция является бесконечно малой функцией, то в этой же окрестности функция () будет бесконечно большой функцией.

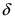
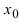
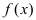
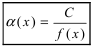
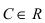
Теорема: Если в некоторой -окрестности точки функция является бесконечно большой функцией, то в этой же окрестности функция () будет бесконечно малой функцией.

Эти теоремы очень часто применяются при вычислении пределов, содержащих бесконечно малые и бесконечно большие функции.

Основные теоремы о пределах

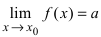
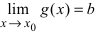
ТЗ. Пусть и . Тогда

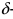
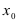
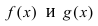
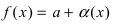
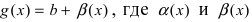
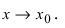
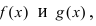
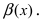
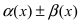
Доказательство: По свойству 4. для бесконечно малых функций в некоторой -окрестности точки функции можно представить в виде: и две бесконечно малые функции при Найдем сумму (разность) функций имеем По свойству 1. для бесконечно малых функций величина является бесконечно малой функцией, следовательно, по свойству 5. для бесконечно малых функций получим

Замечание: Другими словами данную теорему можно сформулировать так: если функции 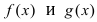имеют конечные пределы а и b, то предел от суммы ( разности) будет равен сумме (разности) пределов от этих функций, т.е.

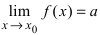
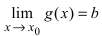
T4. Пусть и . Тогда

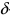
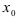
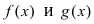
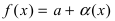
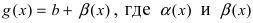
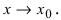
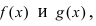
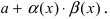
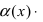
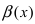
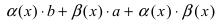
Доказательство: По свойству 4. для бесконечно малых функций в некоторой -окрестности точки функции можно представить в виде: и две бесконечно малые функции при Найдем произведение функций имеем По свойству 2. для бесконечно малых функций величина является бесконечно малой функцией. По свойству 1. для бесконечно малых функций величина является бесконечно малой функцией, следовательно, по свойству 5 для бесконечно малых функций получим

Замечание: Иначе данную теорему можно сформулировать так: если функции f(х) и g(x) имеют конечные пределы а и b, то предел от произведения функций будет равен произведению пределов от этих функций, т.е.

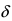
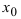
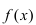
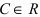
Теорема: Если в некоторой -окрестности точки функция постоянна и равна С (), то ее предел равен С.

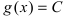
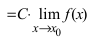
Следствие: из теорем: если , тo

, т.е. постоянный множитель можно выносить за знак предела.

Следствие: Предел степени функции 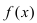равен степени предела этой функции, т.е.

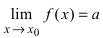
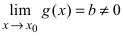
Тб. Пусть и . Тогда

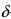
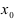
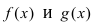
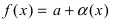
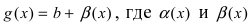
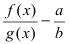
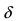
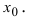
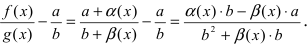
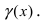
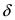
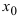
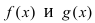
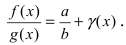
Доказательство: По свойству 4. для бесконечно малых функций в некоторой -окрестности точки функции можно представить в виде: и — две бесконечно малые функции при

в -окрестности точки С учетом выше сказанного имеем В числителе дроби стоит бесконечно малая функция (свойство 1 для бесконечно малых функций), а в знаменателе дроби стоит ограниченная функция. По свойству 7. для бесконечно малых функций дробь в целом представляет собой бесконечно малую функцию Следовательно, в -окрестности точки отношение функций может быть представлено в виде Отсюда по свойству 5. для бесконечно малых функций получим, что

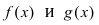
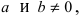
Замечание: Сформулируем теорему иначе: если функции имеют конечные пределы то предел от отношения функций будет равен отношению пределов от этих функций, т.е.

Вычисление пределов и раскрытие неопределенностей

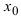
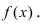
Вычисление любых пределов начинается с подстановки предельного значения аргумента в подлимитную функцию Если при этом полу- чается число, то это число и будет пределом данной функции.

Пример:

Вычислить

Решение:

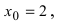
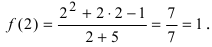
Подставим в функцию значение получим Таким образом,

Пример:

Вычислить

Решение:

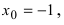
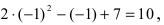
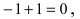
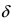
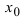
Если подставить в функцию предельное значение то числитель дроби стремится к а знаменатель дроби стремится к т.е. в некоторой -окрестности точки является бесконечно малой функцией. Воспользуемся теоремой, величина обратная к бесконечно малой функции есть бесконечно большая функция, предел которой равен бесконечности. Следовательно,

Определение: Если при подстановки предельного значения аргумента 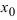в подлимитную функцию возникают выражения вида и им подобные, то говорят о наличии неопределенности.

Определение: Процесс нахождения пределов, имеющих неопределенность, называется раскрытием неопределенностей.

Рассмотрим некоторые приемы раскрытия неопределенностей:

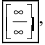
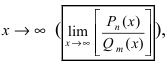
1. Неопределенность типа возникающая при вычислении предела от отношения двух полиномов при раскрывается путем деления числителя и знаменателя на аргумент в высшей степени и использования теореме о связи б.б.ф. с б.м.ф., предел которой равен 0.

Пример:

Найти

Решение:

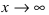
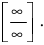
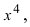
При и числитель, и знаменатель дроби стремятся к бесконечности, поэтому имеем неопределенность вида Высший показатель степени равен 4 и находится в числителе дроби. Разделим числитель и знаменатель дроби на получим

Пример:

Найти

Решение:

Пример:

Найти

Решение:

Рассмотренные примеры позволяют сделать следующий вывод:

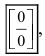
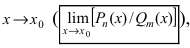
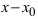
2. Неопределенность типа возникающая при вычислении предела от отношения двух полиномов при раскрывается путем разложения полимонов на простые множители и дальнейшего сокращения числителя и знаменателя дроби на обнуляющий их множитель (при этом используются формулы

Пример:

Найти

Решение:

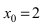
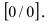
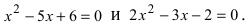
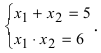
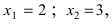
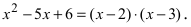
Подстановка предельного значения аргумента в подлимитную функцию приводит к обнулению числителя и знаменателя дроби. Следовательно, дробь приводится к неопределенности Для раскрытия этой неопределенности разложим числитель и знаменатель дроби на простые множители, для чего решим следующие уравнения: По теореме Виета находим Следовательно, а разложение полинома имеет вид: Решим уравнение:

Следовательно, разложение этого полинома на простые множители будет иметь вид: 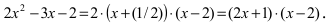Подставим найденные разложения полиномов в исходный предел, получим

Подставляя вместо переменной х ее предельное значение 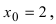получим ответ:

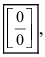
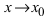
3. Неопределенность типа возникающая при вычислении предела, со- держащего квадратные корни, при раскрывается с использованием фор- мулы, определяющей разность квадратов

Пример:

Найти

Решение:

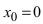
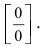
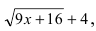
Подстановка предельного значения аргумента в подлимитную функцию приводит к обнулению числителя и знаменателя дроби. Следовательно, дробь приводится к неопределенности Для раскрытия этой неопределённости умножим числитель и знаменатель дроби на выражение получим:

Пример:

Найти

Решение:

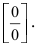
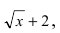
Устремляя х к 4, получим неопределенность Для раскрытия этой неопределённости умножим числитель и знаменатель дроби на выражение а знаменатель и числитель дроби на выражение

Пример:

Найти

Решение:

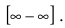
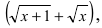
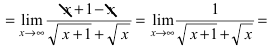
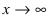
Устремляя x к бесконечности, получим неопределенность Умножим числитель и знаменатель дроби на выражение получим

(знаменатель дроби стремится к бесконечности, следовательно, дробь по теореме при стремится к

Бесконечно малые и бесконечно большие функции

Математическая интерпретация явления часто заключается в том, что практически очень малые величины принимаются за бесконечно малые. Так, рассматривая годовое производство, мы можем отдельный день представить себе как бесконечно малую частицу годового периода и получать при этом практически верные результаты.

Функция y=f(x) называется бесконечно малой при 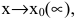если ее предел равен нулю:

Функция y=f(x) называется бесконечно большой при 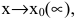если ее предел равен бесконечности:

Теорема 1. Алгебраическая сумма и произведение конечного числа бес-

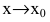
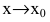
конечно малых функций при есть бесконечно малая функция при .

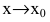
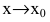
Теорема 2. Произведение бесконечно малой при функции на ограниченную есть бесконечно малая функция при .

Пример №28

Решение:

Если 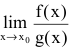не существует, то f(x) и g(x) называют несравнимыми бесконечно малыми при

Если 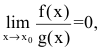то функция f(x) стремится к нулю быстрее, чем g(x)

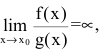
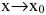
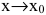
Если то f(x) называют бесконечно малой более низкого порядка, чем g(x) при и пишут: g(x)=o(f(x)), .

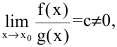
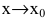
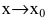
Если то f(x) и g(x) называют бесконечно малыми одного порядка при и пишут: f(x)=O(g(x)), .

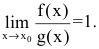
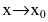
Особенно важен частный случай, когда Тогда f(x) и g(x) называют эквивалентными бесконечно малыми при и пишут: f(x)

g(x), .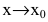

Пример №29

Показать, что 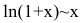при

Решение:

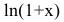
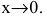
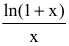
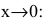
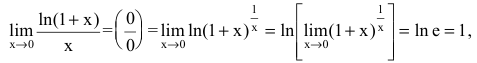
Функции и х являются бесконечно малыми Найдем предел их отношения при что и требовалось доказать. (Переход к пределу под символом логарифма возможен, т.к. логарифмическая функция непрерывна.)

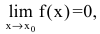
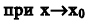
Утверждение. Если то следующие функции экви- валентны: Данная цепочка эквивалентностей используется при нахождении преде- лов.

Теорема 3. Предел отношения двух бесконечно малых функций не изменится, если эти бесконечно малые заменить им эквивалентными.

Пример №30

Вычислить предел

Решение:

Для нахождения предела используем свойства эквивалентности бесконечно малых функций:

Пример №31

Вычислить предел

Решение:

Используя теорему об эквивалентных бесконечно малых, получаем:

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник