Что такое броуновское движение

Броуновское движение в физике

Содержание:

Определение

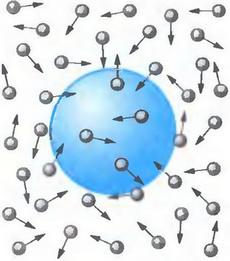
Броуновским движением называется хаотическое и беспорядочное движение маленьких частиц, как правило, молекул в разных жидкостях или газах. Причиной возникновения броуновского движения является столкновение одних (более мелких частиц) с другими частицами (уже более крупными). Какая история открытия броуновского движения, его значение в физике, и в частности в атомно-молекулярной теории? Какие примеры броуновского движения есть в реальной жизни? Обо всем этом читайте далее в нашей статье.

Открытие

Первооткрывателем броуновского движения был английский ботаник Роберт Броун (1773-1858), собственно именно в его честь оно и названо «броуновским». В 1827 году Роберт Броун занимался активными исследованиями пыльцы разных растений. Особенно сильно его интересовало, то, какое участие пыльца принимает в размножении растений. И вот как то, наблюдая в микроскоп движение пыльцы в овощном соке, ученый заметил, что мелкие частицы то и дело совершают случайные извилистые движения.

Наблюдение Броуна подтвердили и другие ученые. В частности было подмечено, что частицы имеют свойство ускоряться с увеличением температуры, а также с уменьшением размера самих частиц. А при увеличении вязкости среды, в которой они находились, их движение наоборот, замедлялось.

Роберт Броун, открыватель броуновского движения.

Сначала Роберт Броун подумал, что он наблюдает движение, даже «танец» каких-то живых микроорганизмов, ведь и сама пыльца – это, по сути, мужские половые клетки растений. Но похожее движение имели и частицы мертвых растений, и даже растений засушенных сто лет назад в гербариях. Еще больше удивился ученый, когда стал исследовать неживую материю: мелкие частицы угля, сажи, и даже частички пыли лондонского воздуха. Затем под микроскоп исследователя попало стекло, различные и разнообразные минералы. И везде были замечены эти «активные молекулы», пребывающие в постоянном и хаотичном движении.

Это интересно: вы и сами можете наблюдать броуновское движение своими глазами, для этого вам понадобится не сильный микроскоп (ведь во время жизни Роберта Броуна еще не было мощных современных микроскопов). Если рассматривать через этот микроскоп, например, дым в зачерненной коробке и освещенный боковым лучом света, то можно будет увидеть маленькие кусочки сажи и пепла, которые будут непрерывно скакать туда-сюда. Это и есть броуновское движение.

Атомно-молекулярная теория

Открытое Броуном движение вскоре стало очень известным в научных кругах. Сам первооткрыватель с удовольствием показывал его многим своим коллегам. Однако долгие годы и сам Роберт Броун, ни его коллеги не могли объяснить причины возникновения броуновского движения, то почему оно вообще происходит. Тем более что броуновское движение было совершенно беспорядочным и не поддавалось никакой логике.

Его пояснение было дано лишь в конце ХIX века и оно не сразу было принято научным сообществом. В 1863 году немецкий математик Людвиг Кристиан Винер предположил, что броуновское движение обусловлено колебательными движениями неких невидимых атомов. По сути это было первое объяснение этого странного явления, связанное со свойствами атомов и молекул, первая попытка при помощи броуновского движения проникнуть в тайну строения материи. В частности Винер попытался измерить зависимость скорости движения частиц от их размера.

Впоследствии идеи Винера были развиты другими учеными, среди них был известный шотландский физик и химик Уильям Рамзай. Именно ему удалось доказать, что причиной броуновского движения мелких частиц являются удары на них еще более мелких частиц, которые в обычный микроскоп уже не видны, подобно тому, как не видны с берега волны качающие далекую лодку, хотя движение самой лодки видно вполне ясно.

Уильям Рамзай в своей лаборатории.

Теория броуновского движения

Несмотря на внешний беспорядок хаотического движения частиц, их случайные перемещения все-таки попытались описать математическими формулами. Так родилась теория броуновского движения.

К слову, одним из тех, кто разрабатывал эту теорию, был польский физик и математик Мариан Смолуховский, который как раз в то время работал во Львовском университете и жил в родном городе автора этой статьи, в прекрасном украинском городе Львове.

Львовский университет, ныне университет им. И. Франка.

Параллельно с Смолуховским теорией броуновского движения занимался один из светочей мировой науки – знаменитый Альберт Эйнштейн, который в то время еще был молодым и никому известным работником в Патентном бюро швейцарского города Берна.

Оба ученых в результате создали свою теорию, которую можно также называть теорией Смолуховского-Эйнштейна. В частности была сформирована математическая формула, согласно нее среднее значение квадрата смещения броуновской частицы (s 2 ) за время t прямо пропорционально температуре Т и обратно пропорционально вязкости жидкости n, размеру частицы r и постоянной Авогадро.

R в формуле – газовая постоянная. Так, если за 1 мин частица диаметром 1 мкм сместится на 10 мкм, то за 9 мин – на 10 = 30 мкм, за 25 мин – на 10= 50 мкм и т.д. В аналогичных условиях частица диаметром 0,25 мкм за те же отрезки времени (1, 9 и 25 мин) сместится соответственно на 20, 60 и 100 мкм, так как = 2. Важно, что в приведенную формулу входит постоянная Авогадро, которую таким образом, можно определить путем количественных измерений перемещения броуновской частицы, что и сделал французский физик Жан Батист Перрен.

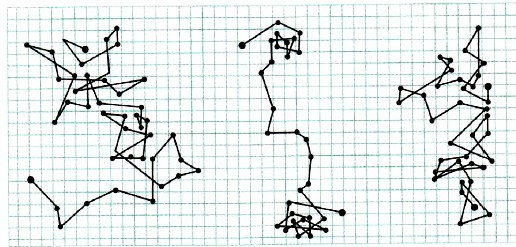
Для наблюдений за броуновскими частицами Перрен использовал новейший на то время ультрамикроскоп, через который уже были видны мельчайшие частицы вещества. В своих опытах ученый, вооружившись секундомером, отмечал положения тех или иных броуновских частиц через равные интервалы времени (например, через 30 секунд). Затем соединяя положения частиц прямыми линями, получались разнообразные замысловатые траектории их движения. Все это зарисовывались на специальном разграфленном листе.

Так выглядели эти рисунки.

Составляя теоретическую формулу Эйнштейна со своими наблюдениями Перрен смог получить максимально точное для того времени значение числа Авогадро: 6,8 . 10 23

Своими опытами он подтвердил теоретические выводы Эйнштейна и Смолуховского.

Диффузия

Перемещения частиц при броуновском движении, внешне очень похоже с движением частиц при диффузии – взаимному проникновению молекул разных веществ под действием температуры. Тогда в чем же различие между броуновским движением и диффузией? В действительности, и диффузия и броуновское движение происходят по причине хаотического теплового движения молекул, и как результат описываются похожими математическими правилами.

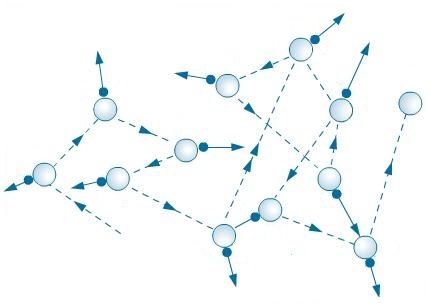
Разница между ними в том, что при диффузии молекула всегда движется по прямой линии, пока не столкнется с другой молекулой, после чего она изменит траекторию своего движения. Броуновская частица «свободного полета» не совершает, а испытывает очень мелкие и частые как бы «дрожания», вследствие которых она хаотически перемещается то туда, то сюда. Говоря образным языком, броуновская частица подобна пустой банки пива, валяющейся на площади, где собралась большая толпа народу. Люди снуют туда-сюда, задевают банку своими ногами и она летает хаотически в разные стороны подобно броуновской частице. А движение самих людей в толпе уже более характерно для движения частиц при диффузии.

Если же смотреть на микро уровне, то причиной движения броуновской частицы является ее столкновение с более мелкими частицами, в то время как при диффузии частицы сталкиваются с себе подобными другими частицами.

И диффузия и броуновское движение происходит под действием температуры. С уменьшением температуры, как скорость частиц при броуновском движении, так и скорость движения частиц при диффузии замедляются.

Примеры в реальной жизни

Теория броуновского движения, этих случайных блужданий имеет и практическое воплощение в нашей реальной жизни. Например, почему, человек, который заблудился в лесу, периодически возвращается на одно и то же место? Потому, что он ходит не кругами, а примерно так, как движется обычно броуновская частица. Поэтому свой собственный путь он пересекает сам много раз.

Поэтому, не имея четких ориентиров и направлений движения, заблудившийся человек уподобляется броуновской частице, совершающей хаотические движения. Но чтобы выйти из леса нужно иметь четкие ориентиры, разработать систему, вместо того, чтобы совершать разные бессмысленные действия. Одним словом, не стоит вести себя в жизни подобно броуновской частице, бросаясь из стороны в сторону, а знать свое направление, цель и призвание, иметь мечты, смелость и упорство их достигать. Вот так из физики мы плавно перешли к философии. На этом заканчиваем эту статью.

Видео

И в завершение образовательное видео по теме нашей статьи.

Автор: Павел Чайка, главный редактор журнала Познавайка

При написании статьи старался сделать ее максимально интересной, полезной и качественной. Буду благодарен за любую обратную связь и конструктивную критику в виде комментариев к статье. Также Ваше пожелание/вопрос/предложение можете написать на мою почту pavelchaika1983@gmail.com или в Фейсбук, с уважением автор.

Эта статья доступна на английском языке – Brownian Motion.

Источник

Броуновское движение

Броуновское движение — это беспорядочные перемещения малых частиц, возникающие вследствие их столкновения с невидимыми молекулами воды или газа. Первым его обнаружил ботаник Роберт Броун — частицы пыльцы, которые он разглядывал под микроскопом на мокром предметном стекле, двигались рывками, — однако описать математически смог только Альберт Эйнштейн. Броуновское движение объясняет, как распространяется в спокойном воздухе пыльца, но и описывает также множество случайных процессов — от наводнений до скачков на фондовом рынке. Его непредсказуемые рывки связаны с фракталами.

В XIX веке ботаник Роберт Броун, разглядывая под микроскопом частицы пыльцы, обнаружил, что они не стоят на месте, но отрывисто двигаются. На миг он задумался — уж не живые ли они? Нет, конечно, просто их сбивали с места молекулы воды, которой Броун смачивал предметные стекла. Частицы пыльцы двигались хаотично, иногда лишь немного, иногда на довольно большие расстояния, и, в конечном счете, совершали по стеклу путь, предсказать который было невозможно. И многие ученые начали задумываться над открытием Броуна, названным в его честь «броуновским движением».

Случайное блуждание

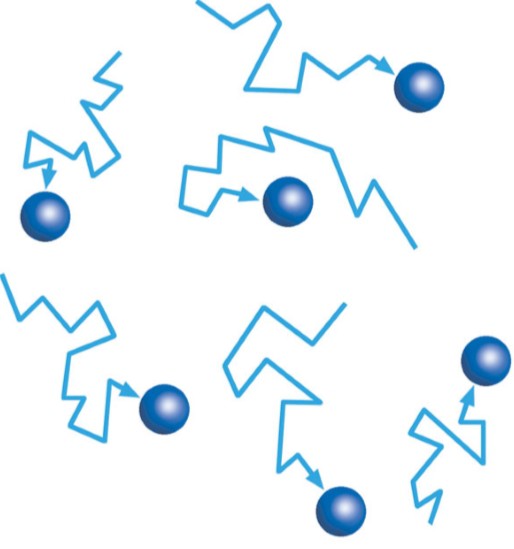
Броуновское движение совершается любыми малыми частицами, находящимися во взвешенном состоянии в жидкости или газе. Его можно наблюдать даже у довольно больших частиц, например частиц дыма, — при большом увеличении видно, какие зигзаги они описывают в воздухе. Сила получаемых частицами ударов зависит от импульса молекул. Она оказывается большей в случае тяжелых молекул жидкости либо газа — как и в случае быстро движущихся, например, молекул нагретой жидкости.

Во второй половине XIX века предпринималась не одна попытка описать броуновское движение математически, однако сделать это смог лишь Эйнштейн в 1905 году, когда он также опубликовал специальную теорию относительности и дал описание фотоэффекта, за что получил Нобелевскую премию. Эйнштейн воспользовался тепловой теорией, основанной на столкновениях молекул, и успешно объяснил движения частиц, которые наблюдал Броун. Поняв, что броуновское движение доказывает существование молекул жидкостей, физики вынуждены были принять и учение об атомах, которое даже в начале XX века еще вызывало сомнения.

Диффузия

Со временем броуновское движение способно заставить частицу пройти значительное расстояние, хоть, разумеется, и не такое, какое она могла бы пройти, если бы никто не мешал ей двигаться по прямой. Это объясняется случайным характером движения молекул, которые с равной вероятностью могут толкать ее и вперед, и назад. Поэтому, если уронить в жидкость плотную группу частиц, они начнут рассеиваться (диффундировать) во все стороны даже при том, что жидкость никто не будет помешивать и никакие потоки в ней не возникнут. Каждая частица пойдет по своему пути, и капля начнет расширяться, образуя диффузное облако. Такое рассеяние играет важную роль в распространении загрязнений воздуха, имеющих точечный источник, например в распространении аэрозоля в атмосфере. Даже при полном отсутствии ветра химические вещества будут рассеиваться в воздухе вследствие одного лишь броуновского движения.

Фракталы

Путь, по которому следует частица, совершающая броуновское движение, дает нам пример фрактала. Каждый прямой отрезок этого пути может иметь любую длину и любое направление, однако некоторый общий рисунок все же существует. Этот рисунок несет в себе определенную структуру, в каком масштабе его ни разглядывай — от наименьшего из вообразимых до очень больших. А это и есть определяющее свойство фрактала.

Фракталы были в 1960-х и 1970-х предложены Бенуа Мандельбротом как метод представления самоподобных фигур в количественной форме. Фракталы — это фигуры, которые при любом масштабе выглядят одинаково. Если увеличить малый кусочек этой фигуры, вы увидите точно такую же, неотличимую от первой, рассматриваемой в большем масштабе, поэтому определить степень увеличения, глядя на фигуру, ни за что не удастся. Такая безмасштабная повторяемость часто встречается в природе — в рисунке береговой линии, в ветвях дерева, в листьях папоротника, в шестикратной симметрии снежинки.

Фракталы отличаются тем, что их длина или размерность не зависят от того, с каким увеличением вы их рассматриваете. Если вы решите измерить расстояние между двумя приморскими городами, Лендс-Эндом и Маунтс-Беем, то, скорее всего, придете к выводу, что оно составляет 30 км, однако вспомните про все береговые скалы и попробуйте обвить каждую веревкой — и вы обнаружите, что веревка вам понадобится в сотню километров длиной. Если же вы пойдете еще дальше и затеете обмерять каждую песчинку берега, веревку придется удлинить до многих сотен километров. Выходит, что абсолютная длина береговой линии зависит от масштаба, в котором вы проводите измерения. Ограничьтесь грубым очертанием берега — и вы снова вернетесь к уже знакомым вам 30 км. В этом смысле фрактальная размерность есть мера огрубления чего-то, будь то облако, дерево или горный хребет. Многие из фрактальных форм, например береговую линию, можно получить соединением шагов случайного движения — отсюда и их связь с броуновским движением.

Математика броуновского движения, или последовательность случайных шагов, может использоваться для создания фрактальных фигур, находящих применение во многих областях науки. С ее помощью можно создавать грубо очерченные виртуальные пейзажи — горы, деревья, облака — компьютерных игр, ее можно использовать в программах пространственного картирования, которые помогают роботам двигаться по сильно пересеченной местности, моделируя ее возвышенности и низины. Врачи применяют ее для медицинской визуализации, когда у них возникает нужда проанализировать структуру сложных органов тела, скажем легких, в которых ветвящиеся структуры присутствуют во всех масштабах, от грубого до совсем малого.

Идеи броуновского движения используются и для предсказания рисков либо событий будущего, которые являются суммарным результатом множества случайных воздействий — наводнений, колебаний фондового рынка. Фондовый рынок можно рассматривать как портфель ценных бумаг, стоимость которых варьируется случайным образом, напоминая броуновское движение множества молекул. Фигурирует оно и в моделировании других социальных процессов, относящихся к производству товаров и принятию решений. Броуновское движение с его случайным характером обладает значительным влиянием и появляется во множестве обличий — не в одном только танце чаинок в чашке горячего чая.

Источник

БРОУНОВСКОЕ ДВИЖЕНИЕ

Броуновское движение частички гуммигута

в воде. Точками отмечены положения частички через каждые 30 сек. (по Перрену). наблюдать совершенно беспорядочное перемещение их, переходы с места на место, сопровождающиеся непрерывным дрожанием. Чем меньше размеры таких частиц, тем ярче проявляется явление: при размерах свыше 0,004 мм движение практически прекращается. Б. д. дает возможность проследить за нек-рыми особенностями молекулярного движения, недоступного для непосредственного наблюдения. Оказывается, что каждую частицу, видимую в микроскоп, можно рас- сматривать как гигантскую «молекулу». Настоящие молекулы, движущиеся вокруг такой частицы, наносят ей со всех сторон удары; если размеры частицы слишком велики, то действие всех ударов взаимно уничтожается, и никаких перемещений частицы наблюдать нельзя. Напротив, если частица достаточно мала, то из огромного числа ударов, наносимых ей, начинают выделяться нек-рые, особенно сильные,—те, которые наносятся молекулами, движущимися с особенно большими скоростями. Под действием таких ударов, резко выделяющихся среди остальных, частицы приходят в движение, заметное в микроскоп. Б. д. иллюстрирует характер и законы теплового движения невидимых молекул. Но, помимо этого, оно позволяет наглядно проследить за распределением частиц в поле тяготения и найти полную аналогию между таким распределением и изменением плотности воздуха по мере поднятия над поверхностью земли. Для этого достаточно в капиллярную трубочку, наполненную водой, внести каплю спиртового раствора мастики. Тогда образовавшиеся в воде мельчайшие частицы мастики будут падать под действием силы тяжести и распределяться на различных уровнях в полном согласии с т. н. барометрической формулой: внизу будет наибольшая концентрация частиц, а чем выше, тем она будет меньше. Изучение Б. д. послужило ряду целей молекулярной физики: оказалось возможным вычислить несколько универсальных постоянных, изучить детально явления диффузии и осмоса. Большое значение оно получило для точного истолкования так называемого второго принципа термодинамики. Лит.: П е р р е н Ж., Атомы, Москва, 1925; Грим зель Э., Курс физики, ч. 3, М. — Л., 1926; Хвольсон О. Д., Курс физики, тт. III и V, Берлин, 1923. В. Шулейкин. Б. д. в биол. отношении представляет значительный интерес для изучения коллоидных свойств протоплазмы при разных физиологических, resp. физ.-химических, состояниях клеток и может указывать на степень ее вязкости, а косвенным путем—и на осмотические свойства и активную реакцию окружающей среды. Наличие или отсутствие в клетках Б. д. не может служит показателем их жизни или смерти. Наблюдения Гайдукова (1910 г.) над различными клетками Vallisneria показали, что временная остановка внутриклеточных токов протоплазмы, поскольку она связана с ее желатинизацией, влечет за собой и приостановку Б. д., но поскольку этот процесс обратим, то разжижение протоплазмы влечет за собой возобновление как внутриклеточных токов, так и Б. д. Для наблюдения Б. д. в животных клетках наилучший объект — нейтрофильные лейкоциты, особенно в слюне, в виде т. н. слюнных телец. Однако, в протоплазме нейтрофилов движение зернистостей наблюдается не только в нормально-подвижных свежих экземплярах, но и в клетках отмирающих, где в условиях осмотической гипотонии, в связи с разбуханием протоплазмы и понижением ее вязкости, движение зернистых частиц принимает постепенно все более хаотический

характер Б., д., при чем движение продолжается и вне клеток после их разрушения.

Лит.: Schade Н. u. W е i 1 е г L., Beitrage zur Kenntnis des Protoplasma menschlieher Zellen bei physiko-chemischer Beeinflussung, Protoplasma, B.III, 1927; Bayliss W., General physiology, L., 1920.

Полезное

Смотреть что такое «БРОУНОВСКОЕ ДВИЖЕНИЕ» в других словарях:

БРОУНОВСКОЕ ДВИЖЕНИЕ — (брауновское движение), беспорядочное движение малых ч ц, взвешенных в жидкости или газе, происходящее под действием ударов молекул окружающей среды. Исследовано в 1827 англ. учёным Р. Броуном (Браун; R. Brown), к рый наблюдал в микроскоп… … Физическая энциклопедия

БРОУНОВСКОЕ ДВИЖЕНИЕ — (брауновское движение) беспорядочное движение мельчайших частиц, взвешенных в жидкости или газе, под влиянием ударов молекул окружающей среды; открыто Р. Броуном … Большой Энциклопедический словарь

БРОУНОВСКОЕ ДВИЖЕНИЕ — БРОУНОВСКОЕ ДВИЖЕНИЕ, неупорядоченное, зигзагообразное движение частиц, взвешенных в потоке (жидкости или газа). Вызывается неравномерностью бомбардировки более крупных частиц с разных сторон более мелкими молекулами движущегося потока. Это… … Научно-технический энциклопедический словарь

броуновское движение — – колебательное, вращательное или поступательное движение частиц дисперсной фазы под действием теплового движения молекул дисперсионной среды. Общая химия : учебник / А. В. Жолнин [1] … Химические термины

БРОУНОВСКОЕ ДВИЖЕНИЕ — бес порядочное движение мельчайших частиц, взвешенных в жидкости или газе, под влиянием ударов молекул окружающей среды, находящихся в тепловом движении; играет важную роль в некоторых физ. хим. процессах, ограничивает точность… … Большая политехническая энциклопедия

броуновское движение — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN Brownian motion … Справочник технического переводчика

Броуновское движение — Эта статья или раздел нуждается в переработке. Пожалуйста, улучшите статью в соответствии с правилами написания статей … Википедия

броуновское движение — (брауновское движение), беспорядочное движение мельчайших частиц, взвешенных в жидкости или газе, под влиянием ударов молекул окружающей среды; открыто Р. Броуном. * * * БРОУНОВСКОЕ ДВИЖЕНИЕ БРОУНОВСКОЕ ДВИЖЕНИЕ (брауновское движение),… … Энциклопедический словарь

БРОУНОВСКОЕ ДВИЖЕНИЕ — непрерывное хаотичное движение микроскопических частиц, взвешенных в газе или жидкости, обусловленное тепловым движением молекул окружающей среды. Это явление впервые было описано в 1827 шотландским ботаником Р.Броуном, исследовавшим под… … Энциклопедия Кольера

Броуновское движение — правильнее брауновское движение, беспорядочное движение малых (размерами в нескольких мкм и менее) частиц, взвешенных в жидкости или газе, происходящее под действием толчков со стороны молекул окружающей среды. Открыто Р. Броуном в 1827.… … Большая советская энциклопедия

Источник

Броуновское движение

Вы будете перенаправлены на Автор24

Что такое Броуновское движение

Броуновским движением называют непрерывное хаотическое движение малых частиц, взвешенных в жидкости или газе.

Это движение характеризуется следующими чертами:

Броуновское движение не является молекулярным движением, но служит непосредственным доказательством существования молекул и хаотического характера их теплового движения.

Сущность Броуновского движения

Сущность этого движения в следующем. Частица вместе с молекулами жидкости или газа образуют одну статистическую систему. В соответствии с теоремой о равномерном распределении энергии по степени свободы на каждую степень свободы приходится 1/2kT энергии. Энергия 2/3kT, приходящаяся на три поступательные степени свободы частицы, приводит к движению ее центра масс, которое наблюдается под микроскопом в виде дрожания частицы. Если броуновская частица достаточно жесткая, то еще 3/2kT энергии приходится на ее вращательные степени свободы. Поэтому при своем дрожании она испытывает еще и постоянные изменения ориентировки в пространстве.

Можно объяснить броуновское движение и так: причиной Броуновского движения являются флуктуации давления, которое оказывается на поверхность малой частицы со стороны молекул среды. Сила и давление изменяется по модулю и направлению, в результате чего частица находится в беспорядочном движении.

Движение броуновской частицы является случайным процессом. Вероятность (dw) того, что броуновская частица, находившаяся в однородной изотропной среде в начальный момент времени (t=0) в начале координат, сместится вдоль произвольно направленной (при t$>$0) оси Ox так, что ее координата будет лежать в интервале от x до x+dx, равна:

Перемещения частицы происходит по сложной ломаной линии все время наблюдений.

Найдем средний квадрат удаления частицы от начала после n шагов в большой серии опытов:

\[\left\langle r^2_n\right\rangle =a^2n=\frac<\triangle t>t=\alpha t=\left\langle r^2\right\rangle \left(4\right),\]

Броуновское движение ограничивает точность измерительных приборов. Предел точности зеркального гальванометра определяется дрожание зеркальца, подобно броуновской частице, которая подвергается ударам молекул воздуха. Случайное движение электронов вызывает шумы в электрических сетях.

Готовые работы на аналогичную тему

Запишем уравнение движения броуновской частицы в проекции на ось Ox:

Аналогичный вид имеют уравнения для величин, относящиеся к другим координатным осям.

Тогда уравнение (1.1) приведем к виду:

Усредним обе части этого уравнения по ансамблю броуновских частиц, учитывая при этом, что средняя от производной по времени равна производной от средней величины, так как это усреднение по ансамблю частиц, и, значит, переставим операцией дифференцирования по времени. В результате усреднения (1.3) получаем:

\[\frac<2>\left(\left\langle \ddot\right\rangle \right)-\left\langle m(\dot)^2\right\rangle =-\frac<2>\left(\dot<\left\langle x^2\right\rangle >\right)+\left\langle F_xx\right\rangle \ \left(1.4\right).\]

Так как отклонения броуновской частицы в любом направлении равновероятны, то:

\[\left\langle x^2\right\rangle =\left\langle y^2\right\rangle =\left\langle z^2\right\rangle =\frac<\left\langle r^2\right\rangle ><3>\left(1.5\right)\]

По теореме о равномерном распределении энергии по степеням свободы:

Таким образом, получим формулу для решения задачи о Броуновском движении:

\[\left\langle r^2\right\rangle =\frac<6kT>t\]

Среднеквадратичная скорость молекул равна:

\[\left\langle v^2\right\rangle =\sqrt<\frac<3kT>>\left(2.1\right)\]

Броуновская частица находится в равновесии с веществом, в котором она находится, и мы можем рассчитать ее среднеквадратичную скорость, используя формулу для скорости молекул газа, которые, в свою очередь, двигаясь, заставляют перемещаться броуновскую частицу. Для начала найдем массу частицы:

\[m_0=\rho V=\frac<4><3>\pi R^3\rho \left(2.2\right)\]

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 16 12 2021

Источник