Что такое буквенное выражение 7 класс
Алгебра. 7 класс
Конспект урока
Перечень рассматриваемых вопросов:
Буквенное выражение – выражение, состоящее из букв, чисел, знаков математических действий и скобок.
1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.
1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.
2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.
3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.
На этом уроке мы узнаем, какие ещё бывают выражения, помимо числовых.
Возьмём, например, такое числовое выражение (15+3): 4 и заменим одно из чисел (или все сразу) буквой. Получится выражение, которое числовым уже нельзя назвать.
Такие выражения называют буквенными.
Буквенное выражение – это выражение, состоящее из букв, чисел, знаков математических действий и скобок.
Например, буквенные выражения могут выглядеть так:
Стоит отметить, что буквенные и числовые выражения называют алгебраическими выражениями.
Например, алгебраическими можно назвать следующие выражения:
Если взять два алгебраических выражения и соединить их знаками арифметических действий (сложения, вычитания, умножения или деления), то всё равно получится алгебраическое выражение.
Возьмём два алгебраических выражения и сложим их.
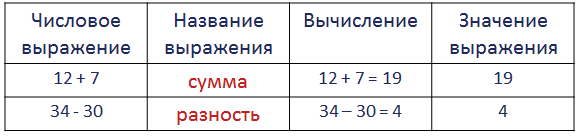
Полученное выражение называется суммой алгебраических выражений.
(2+36:с)+ (23–58•23) – сумма алгебраических выражений.
Возьмём два алгебраических выражения и вычтем из первого второе.
Полученное выражение называется разностью алгебраических выражений.
(2 + 36 : с) – (23 –58 • 23) – разность алгебраических выражений
Возьмём два алгебраических выражения и перемножим их. Полученное выражение называется произведением алгебраических выражений.
(2 + 36 : с) • (23 –58 • 23)
Стоит отметить, что очень часто знак умножения опускают.
(2 + 36 : с)(23– 58•23) – произведение алгебраических выражений.
И, наконец, возьмём два алгебраических выражения и разделим первое на второе.
Полученное выражение называется частным данных алгебраических выражений.
(2 + 36 : с) : (23 – 58 • 23)– частное алгебраических выражений.
Теперь разберёмся, где используют буквенные выражения.
Если с числовыми выражениями всё предельно просто, их используют для вычислений при решении тех или иных задач, в том числе и в других науках, то буквенные выражения просто необходимы при решении задач в общем виде.
Решим такую задачу.
Человек решил положить деньги в банк в сумме а рублей на 3 года. При условии, что банк будет начислять в конце каждого года х% от величины вклада. Сколько рублей будет иметь вкладчик на счёте в конце 3 года?
Решение. Для решения задачи можно использовать таблицу.
Заполним её, исходя из условия задачи.
У нас есть 3 года и один и тот же процент х.
Переведём данный процент в число, получатся следующее алгебраическое выражение:
Далее подсчитаем доход за первый год, для этого сумму вклада умножим на процент, выраженный числом, получается такое буквенное выражение:
Далее рассчитаем сумму на счёте в конце первого года, она будет состоять из суммы вклада и процента, получаем следующее алгебраическое выражение:
И теперь, если вместо букв а и х будут даны определённые числовые значения, останется их только подставить в решение и получить определённый результат.
Стоит отметить, что буквенное выражение может состоять только из буквы.
Разбор заданий тренировочного модуля.
1.Выберите верное выражение по условию задачи. 1кг печенья стоит 200 руб., а 1 кг конфет на х руб. больше. Во сколько раз 1 кг конфет дороже печенья?
Решение: Для решения задачи нужно сначала составить выражение для стоимости конфет. Оно выглядит следующим образом: 200+х руб. А теперь остаётся найти отношение цены за 1 кг конфет к печенью. Выражение выглядит так: (200+х): х.
Следовательно, правильный ответ:(200+х): х.
2. В течение года цена на квартиру поднялась на к%, а ещё через год увеличилась ещё на х%. На сколько процентов увеличилась цена на квартиру за 2 года? Выберите правильное выражение, которое характеризует ответ на поставленный вопрос.
Решение: Для решения задачи обозначим первоначальную стоимость за 100 %, тогда цена за квартиру в первый год составит (100+ к)%.
Найдем процент повышения цены за второй год от новой стоимости, выраженной в процентах. Получим следующее
Остаётся найти, на сколько процентов увеличилась цена на квартиру за 2 года. Для этого найдем разность между новой ценой за 2 год и первоначальной стоимостью.
Числовые и буквенные выражения
Числовые выражения
В этом разделе мы узнаем, что называют числовым выражением и значением выражения, научимся читать выражения.
Значение выражения — это результат выполненных действий.
Чтение числовых выражений
Решение числовых выражений
45 – (30 + 2) = …
Сначала выполняем действие, записанное в скобках. К 30 прибавляем 2.
30 + 2 = 32
Теперь нужно из 45 вычесть 38.
45 – 32 = 13
45 – (30 + 2) = 13
Сравнение значений числовых выражений
Сравнить числовое выражение – найти значение каждого из выражений и их сравнить.
Для этого найдем значения каждого из них:
Буквенные выражения
Буквенным называется математическое выражение, в котором используются цифры, знаки действий и буквы. Например, (47 + d) – 11.
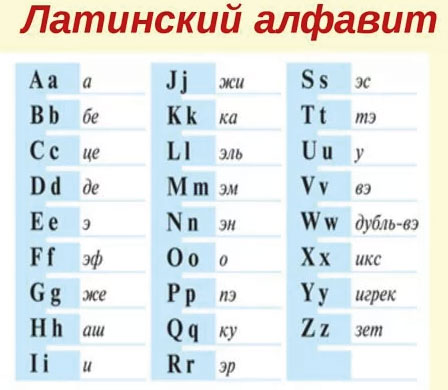
Для записи буквенных выражений необходимо знать некоторые буквы латинского алфавита. Мы приводим его полностью, чтобы ты знал, с какими буквами можешь встретиться при составлении, решении или чтении буквенных выражений.
Чаще всего используются буквы:
a, b, c, d, x, y, k, m, n
Алгоритм решения буквенного выражения
1. Прочитать буквенное выражение
2. Записать буквенное выражение
3. Подставить значение неизвестного в выражении
4. Вычислить результат
Читаем выражение: Из 28 вычесть с или Найти разность числа 28 и с
Подставим вместо неизвестного «с» число 4.
У нас получается выражение: 28 – 4
Переменные
Буквы, которые содержатся в буквенных выражениях называются переменными. Например, в выражении с + x + 2 переменными являются буквы c и x. Если вместо этих переменных подставить любые числа, то буквенное выражение с + x + 2 обратится в числовое выражение, значение которого можно будет найти.
Числа, которые подставляют вместо переменных называют значениями переменных. Например, изменим значения переменных c и x. Для изменения значений используется знак равенства
Мы изменили значения переменных c и x. Переменной c присвоили значение 2, переменной x присвоили значение 3, тогда выражение с + х + 2 будет выглядеть так:
Теперь мы можем найти значение этого выражения:
с + х + 2 = 2 + 3 + 2 = 5 + 2 = 7
Поделись с друзьями в социальных сетях:
Алгебра. 7 класс
Конспект урока
Перечень рассматриваемых вопросов:
Буквенное выражение – выражение, состоящее из букв, чисел, знаков математических действий и скобок.
1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.
1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.
2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.
3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.
На этом уроке мы узнаем, какие ещё бывают выражения, помимо числовых.
Возьмём, например, такое числовое выражение (15+3): 4 и заменим одно из чисел (или все сразу) буквой. Получится выражение, которое числовым уже нельзя назвать.
Такие выражения называют буквенными.
Буквенное выражение – это выражение, состоящее из букв, чисел, знаков математических действий и скобок.
Например, буквенные выражения могут выглядеть так:
Стоит отметить, что буквенные и числовые выражения называют алгебраическими выражениями.
Например, алгебраическими можно назвать следующие выражения:
Если взять два алгебраических выражения и соединить их знаками арифметических действий (сложения, вычитания, умножения или деления), то всё равно получится алгебраическое выражение.
Возьмём два алгебраических выражения и сложим их.
Полученное выражение называется суммой алгебраических выражений.
(2+36:с)+ (23–58•23) – сумма алгебраических выражений.
Возьмём два алгебраических выражения и вычтем из первого второе.
Полученное выражение называется разностью алгебраических выражений.
(2 + 36 : с) – (23 –58 • 23) – разность алгебраических выражений
Возьмём два алгебраических выражения и перемножим их. Полученное выражение называется произведением алгебраических выражений.
(2 + 36 : с) • (23 –58 • 23)
Стоит отметить, что очень часто знак умножения опускают.
(2 + 36 : с)(23– 58•23) – произведение алгебраических выражений.
И, наконец, возьмём два алгебраических выражения и разделим первое на второе.
Полученное выражение называется частным данных алгебраических выражений.
(2 + 36 : с) : (23 – 58 • 23)– частное алгебраических выражений.
Теперь разберёмся, где используют буквенные выражения.
Если с числовыми выражениями всё предельно просто, их используют для вычислений при решении тех или иных задач, в том числе и в других науках, то буквенные выражения просто необходимы при решении задач в общем виде.
Решим такую задачу.
Человек решил положить деньги в банк в сумме а рублей на 3 года. При условии, что банк будет начислять в конце каждого года х% от величины вклада. Сколько рублей будет иметь вкладчик на счёте в конце 3 года?
Решение. Для решения задачи можно использовать таблицу.
Заполним её, исходя из условия задачи.
У нас есть 3 года и один и тот же процент х.
Переведём данный процент в число, получатся следующее алгебраическое выражение:
Далее подсчитаем доход за первый год, для этого сумму вклада умножим на процент, выраженный числом, получается такое буквенное выражение:
Далее рассчитаем сумму на счёте в конце первого года, она будет состоять из суммы вклада и процента, получаем следующее алгебраическое выражение:
И теперь, если вместо букв а и х будут даны определённые числовые значения, останется их только подставить в решение и получить определённый результат.
Стоит отметить, что буквенное выражение может состоять только из буквы.
Разбор заданий тренировочного модуля.
1.Выберите верное выражение по условию задачи. 1кг печенья стоит 200 руб., а 1 кг конфет на х руб. больше. Во сколько раз 1 кг конфет дороже печенья?
Решение: Для решения задачи нужно сначала составить выражение для стоимости конфет. Оно выглядит следующим образом: 200+х руб. А теперь остаётся найти отношение цены за 1 кг конфет к печенью. Выражение выглядит так: (200+х): х.
Следовательно, правильный ответ:(200+х): х.
2. В течение года цена на квартиру поднялась на к%, а ещё через год увеличилась ещё на х%. На сколько процентов увеличилась цена на квартиру за 2 года? Выберите правильное выражение, которое характеризует ответ на поставленный вопрос.
Решение: Для решения задачи обозначим первоначальную стоимость за 100 %, тогда цена за квартиру в первый год составит (100+ к)%.
Найдем процент повышения цены за второй год от новой стоимости, выраженной в процентах. Получим следующее
Остаётся найти, на сколько процентов увеличилась цена на квартиру за 2 года. Для этого найдем разность между новой ценой за 2 год и первоначальной стоимостью.
Числовые выражения и буквенные выражения — правила
При решении примеров и уравнений нужно четко отличать — что такое числовые выражение, а что такое буквенные выражения. Поэтому сегодня пройдем эту тему и посмотрим видео. Итак, выучите правила.
Правила математики о числовых и буквенных выражениях
Число, которое получается в результате выполнения математических операций, входящих в это числовое выражение, называется значением числового выражения.
Числа, которые заменяют букву, называются значениями этой буквы.
Чтобы запомнить правила, давайте обратимся к примерам. Примеры — самый простой наглядный способ запомнить утверждения, приведенные выше.
Примеры числовых выражений
— в левой части этого равенства стоит числовое выражение, а в правой части — значение числового выражения.
— в левой части равенства — числовое выражение, а в правой части — значение числового выражения.
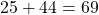
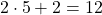
Посмотрите еще примеры числовых выражений:
Примеры буквенных выражений
Примеры буквенных выражений:
Буквенных выражений может быть множество. Для буквенных выражений каждая буква — это определенное число. Или множество разных чисел.
Когда применяются буквенные выражения
Буквенные выражения применяются тогда, когда нам надо, например, ввести формулу для нахождения той или иной величины. Например, вы знаете — что периметр прямоугольника, это сумма всех его сторон. Для периметра в общем виде можно записать буквенное выражение:
, где 
— ширина прямоугольника, а 
— его длина.
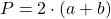
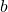
В правой части вы увидели буквенное выражение, значениями букв и — будут числа — значения ширины и длины прямоугольника.
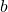
Математические выражения
— это математическое выражение.
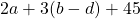
Число перед буквой в математическом выражении — это коэффициент, означающий, что это число умножается на букву, которая может иметь переменное значение.
Буквенные, числовые и математические выражения — необходимо различать, чтобы понимать условия задачи, например, вас могут попросить упростить математическое выражение или попросить найти значение числового выражения. Поэтому необходимо знать — что это такое.
Числовые, буквенные выражения и выражения с переменными: определения, примеры
В математике принято использовать свои обозначения. Запись условий задач с их помощью приводит к появлению так называемых математических выражений. Можно говорить про числовые, буквенные выражения и математические выражения с переменными. Для удобства и одни, и вторые и третьи называются просто выражениями. В этой статье мы дадим определения и по порядку рассмотрим каждый тип математических выражений.
Числовые выражения
Конечно, числовые выражения содержат не только знаки «плюс» и «минус». Они могут включать деление и умножение, содержать скобки, степени, корни, логарифмы и состоять из нескольких действий.
Учитывая все сказанное, дадим определение. Что такое числовое выражение?
Определение. Числовое выражение
Числовым выражением считается только та комбинация, которая составлена с учетом математических правил.
Поясним данное определение.
Во-первых, числа. Математическое выражение может содержать любые числа. Это значит, что в математическом выражении можно встретить:
деление в выражениях может присутствовать как в виде знака, так и в виде дробной черты.
Скобки в числовых выражениях
Согласно определению, числовые выражения могут содержать степени, корни, логарифмы, тригонометрические и обратные тригонометрическим функции. Приведем пример такого числового выражения:
В качестве примера использования в числовых выражениях специальных знаков, можно привести знак модуля.
Буквенные выражения
После знакомства с числовыми выражениями можно вводить понятие буквенных выражений. Интуитивно понятно, что в них вместо чисел используются буквы. Но обо всем по порядку.
Запишем числовое выражение, но вместо одного числа оставим пустой квадратик.
Определение. Буквенное выражение
Выражение, в котором буквы заменяняют некоторые цифры, называется буквенным выражением. Буквенное выражение должно содержать по крайней мере одну букву.
Приведем пример сложного буквенного выражения.
Выражения с переменными
В рассмотренных выше буквенных выражениях буква обозначала какое-то конкретное числовое значение. Величина, которая может принимать ряд различных значений, называется переменной. Выражение с такой величиной, соответственно, называются выражением с переменной.
Определение. Выражения с переменными
Вообще буквенные выражения и выражения с переменными позволяют посмотреть на задачу вне контекста конкретных чисел, то есть более широко. Они широко используются в математическом анализе для формулировок и доказательств.
Внешний вид буквенного выражения не позволяет узнать, являются входящие в него буквы переменными, или нет. Для этого нужно знать условия конкретной задачи, описываемой выражением. Вне контекста ничто не мешает считать входящие в выражение буквы переменными. Таким образом, разница между понятиями «буквенное выражение» и «выражение с переменными» нивелируется.