Национальная библиотека им. Н. Э. Баумана
Bauman National Library

Персональные инструменты

Булева алгебра

Содержание

Определение

Булева алгебра как предметная область определяется следующими критериями:

Происхождение

Булева алгебра названа по имени великого английского математика Джорджа Буля (1815—1864), который в 1854 г. опубликовал ставшую впоследствии знаменитой книгу «Исследование законов мышления». В начале гл. 1 он написал: «Назначение настоящего трактата — исследовать основные законы тех операций ума, посредством которых производится рассуждение; выразить их на символическом языке некоторого исчисления и на этой основе установить науку логики и построить ее метод; сделать этот метод основой общего применения математической доктрины вероятностей; и, наконец, собрать из различных элементов истины, выявленных в ходе этих изысканий, некоторые правдоподобные указания относительно природы и строения человеческого ума».

В этой книге Буль изложил большую часть новой алгебры, особенно пригодную для анализа классов и предложений (высказываний).

Другие математики и логики, в том числе Джон Венн и Эрнст Шрёдер, впоследствии значительно усовершенствовали и расширили алгебру Буля.

В 1938 г. Клод Э. Шеннон, в то время студент Массачусетсского технологического института, впоследствии известный математик и инженер Белловских телефонных лабораторий, а в настоящее время профессор Массачусетского технологического института, показал, что булеву алгебру можно прекрасно применять при синтезе переключательных электрических схем. Его статья «Символический анализ релейно-переключательных схем» представляет собой веху в развитии применений булевой алгебры.

Аксиомы

1) Булева переменная всегда равна либо нулю, либо единице

2) Инверсное значение переменной x противоположно ее прямому значению

3) Правила выполнения логического умножения (конъюнкции)

4) Правила выполнения логического сложения (дизъюнкции)

Законы

1) Ассоциативный (сочетательный) закон

Ассоциативность конъюнкции и дизъюнкции выражается следующими формулами:

На практике это означает, что можно опускать те скобки, которые определяют, в каком порядке должна выполняться конъюнкция и дизъюнкция.

2) Коммутативный (переместительный) закон Правила

С помощью законов алгебры логики можно производить равносильные преобразования логических выражений с целью их упрощения. В алгебре логики на основе принятого соглашения установлены следующие правила (приоритеты) для выполнения логических операций:

первыми выполняются операции в скобках, затем в следующем порядке:

Обозначение на логических схемах

Для обозначения логических элементов используется несколько стандартов. Наиболее распространёнными являются американский (ANSI), европейский (DIN), международный (IEC) и российский (ГОСТ). На рисунке ниже приведены обозначения логических элементов в этих стандартах.

Источник

Булева алгебра. Часть 1. Немного истории

В школе все мы изучали алгебру, только про булеву алгебру там не говорили. Чем отличается булева алгебра от школьной, история ее появления, задачи и области применения описаны в данной статье.

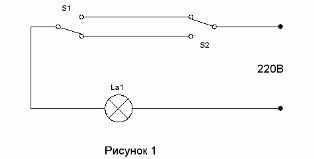
Схема, позволяющая двумя выключателями лампочку в коридоре включить при входе в коридор и выключить, войдя в комнату известна очень давно (cм. Коридорная схема управления освещением). Она показана на рисунке 1.

Задача №1. Более сложная. Составить схему, позволяющую включать и выключать свет в вашей комнате любым из 3 различных выключателей. Выключатели расположены у входа в комнату, над постелью и у письменного стола.

Задача № 2.

В спортивном комитете, например заводском, собралось 5 судей.

Каждый из них должен голосовать за принятие различных решений. Решение принимается большинством голосов, но только при том дополнительном условии, что за него голосует председатель комитета.

Задача №3. Практически такое маловероятно, но в качестве сложной учебной задачи вполне подойдет.

В большой шестиугольной комнате на каждой стене установлено по одному переключателю. Постройте такую схему, чтобы в любой момент можно было включать или выключать свет в комнате поворотом одного (любого) переключателя.

После того, как вы безрезультатно просидите над задачами три-четыре дня, отложите их временно в сторону. И займитесь алгеброй Буля. Именно алгебра Буля, или, как ее еще называют, булева алгебра, алгебра релейных схем, поможет вам решить составленные задачи.

Что же такое алгебра Буля?

Как ни странно, несмотря на то, что пять лет в школе изучают алгебру, многие ученики, а впоследствии и взрослые, не смогут ответить на вопрос, а что такое алгебра? Алгебра — это наука, которая изучает множества некоторых элементов и действия над ними.

В школьном курсе алгебры такими элементами являются числа. Числа можно обозначать не цифрами, а буквами, с этим все знакомы. На первых уроках алгебры это всегда затрудняет многих учеников. Вспомните, как трудно было вначале привыкнуть вместо цифр складывать буквы, решая ничего не говорящие уравнения.

Наверное, каждый из нас тогда задавал себе вопрос: «Для чего нужно вводить буквы вместо цифр и, нужно ли это вообще?». И только позднее вы убедились, какие преимущества при решении задач дает алгебра в сравнении с арифметикой.

Алгебра применяется во многих точных науках. Это физика, механика, сопромат, электричество. Закон Ома есть не что иное, как алгебраическое уравнение: достаточно вместо букв подставить их числовые значения, чтобы узнать какой ток будет протекать в нагрузке, или какое сопротивление имеет участок цепи.

Так вы познакомились с алгеброй чисел, или с элементарной алгеброй. Основная и почти единственная задача — получить ответ на вопрос: «Чему равняется X? Сколько?»

В старших классах школы изучают начала векторной алгебры. Эта алгебра принципиально отличается от элементарной алгебры. В ней совершено другая природа изучаемого множества и другие правила действий. Решая векторное уравнение, получаем в ответе вектор, который не является обычным числом, отвечающим на вопрос «Сколько?»

Формулы векторной алгебры во многом отличны от формул элементарной алгебры. Например, и в элементарной алгебре и в векторной имеется операция сложения. Но выполняется она совершенно по-разному. Сложение чисел выполняется совсем не так, как сложение векторов.

Существуют и другие алгебры: линейная алгебра, алгебра структур, алгебра колец, алгебра логики, или, что то же самое, алгебра Буля. На школьных уроках вы, наверное, не слышали имени Джорджа Буля — зато всем известно имя одной из его талантливых дочерей Этель Войнич (1864 – 1960). Она написала роман «Овод», где рассказывается о борьбе за свои права итальянских карбонариев.

Джордж Буль родился в Англии 2 ноября 1815 года. Всю свою жизнь он работал учителем математики и физики в школе. Из воспоминаний его учеников известно, какое огромное значение придавал Буль развитию творческих способностей учащихся. При изложении нового материала он стремился к тому, чтобы его ученики сами заново «открывали» некоторые формулы и законы.

Рассказывая ученикам о трудностях, с которыми ученые неизбежно сталкивались в поиске истины, учитель любил повторять одну восточную мудрость: даже персидский трон не может принести человеку столько наслаждений, как самое маленькое научное открытие. Буль никогда не терял надежды, что когда-нибудь и его ученики сделают настоящее открытие.

Диапазон научных интересов Буля был очень широк: в равной степени его интересовали математика и логика — наука о законах и формах мышления. В те времена логика считалась гуманитарной наукой, и многих, кто знал Джорджа Буля, удивляло, как в одном человеке могли уживаться точные методы познания, присущие математике, и чисто описательные методы логики.

Но ученому захотелось сделать науку о законах и формах мышления такой же строгой, как и любая из естественных наук, скажем математика и физика. Для этого Буль стал обозначать буквами не числа, как это делается в обычной алгебре, а высказывания и показал, что такими уравнениями, очень схожими с алгебраическими, можно решать вопросы об истинности и ложности высказываний, сделанных человеком. Так возникла алгебра Буля.

Но еще задолго до Джорджа Буля немецкий математик и философ Готфрид Лейбниц (1646—1716) впервые высказал идею о создании науки, которая обозначит все понятия обычной разговорной речи символами и установит некоторую новую алгебру для соединения этих символов.

После создания такой науки, по мнению Лейбница, ученые и философы перестанут спорить и перекрикивать друг друга, выясняя истину, а возьмут в руки карандаш и спокойно скажут: «Давайте-ка вычислять!»

В наши дни алгебра логики стала важнейшей составной частью математики. Одна из ее задач — это решение всевозможных уравнений, числовые соотношения в которых заменены буквенными. Каждый из вас, наверное, на всю свою жизнь запомнил, как решать уравнения второй и третьей степени с буквенными коэффициентами. Так вот, Буль в своей новой алгебре воспользовался всеми этими формулами и правилами.

Новым в алгебре Буля является то, что элементы множества, которые в ней изучаются, являются не числами, а высказываниями. Если при решении обычных алгебраических уравнений определяется, какому числу равняется неизвестное X, школьная алгебра ищет ответ на вопрос: «Сколько?»

Алгебра логики ищет ответ на вопрос: «Верно ли то или другое высказывание, обозначенное буквой X?»

Смысл и содержание высказывания здесь не играют никакой роли. Каждое высказывание может быть только или истинным, или ложным. Оно не может быть наполовину истинным и наполовину ложным. В качестве примера можно вспомнить метание жребия при помощи монеты.

Там рассматриваются только два состояния монеты — орел или решка. По договоренности сторон орел это ДА, а решка это НЕТ. Никакие другие промежуточные положения в теории вероятностей не учитываются, хотя они и возможны. Подброшенная монета может упасть на ребро, докатиться по полу до ножки стула или стола и так и остаться в вертикальном положении, а то и вообще провалиться в широкую щель в полу. (По аналогии с электрическими схемами две последних ситуации можно рассматривать как неисправность в виде обгоревшего контакта). Но в те далекие времена булева алгебра, увы, широкого распространения не получила.

Вновь «открыл» алгебру Буля Клод Шеннон. В 1938 году, будучи еще студентом Массачусетского технологического института и Америке, молодой Клод доказал, что алгебра Буля полностью подходит для анализа и синтеза релейных и переключательных схем.

С помощью алгебры Буля можно очень просто составить электрическую схему автомата, работающего на реле. Для этого, оказывается, нужно только точно знать, что должен делать автомат, то есть нужно иметь алгоритм его работы. Так была заложена основа теории цифровых машин, действующих по принципу ДА или НЕТ.

Такова вкратце история булевой алгебры. В следующих статьях мы рассмотрим ее основные законы, примеры контактных схем реализующие эти законы. Рассмотрим решение тех задач, которые были приведены в начале статьи.

Источник

Булева алгебра

Булевой алгеброй [1] [2] [3] называется непустое множество A с двумя бинарными операциями (аналог конъюнкции), (аналог дизъюнкции), унарной операцией (аналог отрицания) и двумя выделенными элементами: 0 (или Ложь) и 1 (или Истина) такими, что для всех a, b и c из множества A верны следующие аксиомы:

		ассоциативность
		коммутативность
		законы поглощения
		дистрибутивность
		дополнительность

Первые три аксиомы означают, что (A, , ) является решёткой. Таким образом, булева алгебра может быть определена как дистрибутивная решётка, в которой выполнены две последние аксиомы. Структура, в которой выполняются все аксиомы, кроме предпоследней, называется псевдобулевой алгеброй.

Содержание

Некоторые свойства

Из аксиом видно, что наименьшим элементом является 0, наибольшим является 1, а дополнение ¬a любого элемента a однозначно определено. Для всех a и b из A верны также следующие равенства:

		дополнение 0 есть 1 и наоборот
		законы де Моргана
.	инволютивность отрицания, закон снятия двойного отрицания.

Основные тождества

В данном разделе повторяются свойства и аксиомы, описанные выше с добавлением ещё нескольких.

Сводная таблица свойств и аксиом, описанных выше:

		1 коммутативность, переместительность
		2 ассоциативность, сочетательность
3.1 конъюнкция относительно дизъюнкции	3.2 дизъюнкция относительно конъюнкции	3 дистрибутивность, распределительность
		4 комплементность, дополнительность (свойства отрицаний)
		5 законы де Моргана
		6 законы поглощения
		7 Блейка-Порецкого
		8 Идемпотентность
	9 инволютивность отрицания, закон снятия двойного отрицания
		10 свойства констант
дополнение 0 есть 1	дополнение 1 есть 0
		11 Склеивание

Примеры

Принцип двойственности

В булевых алгебрах существуют двойственные утверждения, они либо одновременно верны, либо одновременно неверны. Именно, если в формуле, которая верна в некоторой булевой алгебре, поменять все конъюнкции на дизъюнкции, 0 на 1, ≤ на ≥ и наоборот, то получится формула, также истинная в этой булевой алгебре. Это следует из симметричности аксиом относительно таких замен.

Представления булевых алгебр

Можно доказать, что любая конечная булева алгебра изоморфна булевой алгебре всех подмножеств какого-то множества. Отсюда следует, что количество элементов в любой конечной булевой алгебре будет степенью двойки.

Знаменитая теорема Стоуна утверждает, что любая булева алгебра изоморфна булевой алгебре всех открыто-замкнутых множеств какого-то компактного вполне несвязного хаусдорфова топологического пространства.

Аксиоматизация

В 1933 г. американский математик Хантингтон предложил следующую аксиоматизацию для булевых алгебр:

Здесь использованы обозначения Хантингтона: + означает дизъюнкцию, n — отрицание.

Герберт Роббинс поставил следующий вопрос: можно ли сократить последнюю аксиому так, как написано ниже, то есть будет ли определённая выписанными ниже аксиомами структура булевой алгеброй?

Аксиоматизация алгебры Роббинса:

Этот вопрос оставался открытым с 30-х годов и был любимым вопросом Тарского и его учеников.

В 1996 г. Вильям МакКьюн, используя некоторые полученные до него результаты, дал утвердительный ответ на этот вопрос. Таким образом, любая алгебра Роббинса является булевой алгеброй.

Источник

Булева алгебра

Что такое булева алгебра?

Булева алгебра – это раздел математики, который занимается операциями с логическими значениями и включает двоичные переменные. Булева алгебра берет свое начало в книге математика Джорджа Буля 1854 года.

Отличительной чертой булевой алгебры является то, что она занимается только изучением двоичных переменных. Чаще всего логические переменные представлены с возможными значениями 1 («истина») или 0 («ложь»). Переменные также могут иметь более сложные интерпретации, например, в теории множеств. Булева алгебра также известна как бинарная алгебра.

Ключевые выводы

Понимание булевой алгебры

Булева алгебра отличается от элементарной алгебры, поскольку последняя имеет дело с числовыми операциями, а первая имеет дело с логическими операциями. Элементарная алгебра выражается с помощью основных математических функций, таких как сложение, вычитание, умножение и деление, тогда как булева алгебра имеет дело с конъюнкцией, дизъюнкцией и отрицанием.

Понятие булевой алгебры было впервые введено Джорджем Булем в его книге «Математический анализ логики» и далее расширено в его книге «Исследование законов мысли». Поскольку ее концепция была подробно описана, булевская алгебра в основном использовалась в языках программирования. Его математические цели используются в теории множеств и статистике.

Булева алгебра в финансах

Булева алгебра находит применение в финансах посредством математического моделирования рыночной деятельности. Например, исследованию цен на опционы на акции может помочь использование бинарного дерева для представления диапазона возможных результатов для базовой ценной бумаги. В этой биномиальной модели ценообразования опционов, где есть только два возможных результата, логическая переменная представляет увеличение или уменьшение цены ценной бумаги.

Этот тип моделирования необходим, потому что для американских опционов, которые могут быть исполнены в любое время, траектория цены ценной бумаги так же важна, как и ее окончательная цена. Модель ценообразования биномиальных опционов требует, чтобы траектория цены ценной бумаги была разбита на серию дискретных временных диапазонов.

Таким образом, модель ценообразования биномиальных опционов позволяет инвестору или трейдеру отслеживать изменение цены актива от одного периода к другому. Это позволяет им оценивать вариант на основе решений, принятых на разных этапах. Поскольку опцион в США может быть исполнен в любое время, это позволяет трейдеру определить, следует ли ему исполнять опцион или удерживать его в течение более длительного периода. Анализ биномиального дерева позволит трейдеру заранее увидеть, следует ли исполнять опцион. Если есть положительное значение, то опцион должен быть исполнен, если значение отрицательное, то трейдер должен удерживать позицию.

Источник

Булева алгебра

Булевой алгеброй называется непустое множество A с двумя бинарными операциями (аналог конъюнкции), (аналог дизъюнкции), унарной операцией (аналог отрицания) и двумя выделенными элементами: 0 (или Ложь) и 1 (или Истина) такими, что для всех a, b и c из множества A верны следующие аксиомы :

		ассоциативность
		коммутативность
		законы поглощения
		дистрибутивность
		дополнительность

Содержание

Некоторые свойства

Из аксиом видно, что наименьшим элементом является 0, наибольшим является 1, а дополнение ¬a любого элемента a однозначно определено. Для всех a и b из A верны также следующие равенства:

		дополнение 0 есть 1 и наоборот
		законы де Моргана
	инволютивность отрицания

Основные тождества

В данном разделе повторяются свойства и аксиомы, описанные выше с добавлением еще нескольких.

Сводная таблица свойств и аксиом, описанных выше:

		1 коммутативность
		2 ассоциативность
3.1 конъюнкция относительно дизъюнкции	3.2 дизъюнкция относительно конъюнкции	3 дистрибутивность
		4 дополнительность (свойства отрицаний)
		5 законы де Моргана
		6 законы поглощения
		7 Блейка-Порецкого
		8 Идемпотентность
	9 инволютивность отрицания
		10 свойства констант
дополнение 0 есть 1	дополнение 1 есть 0
		11 Склеивание

Примеры

Принцип двойственности

В булевых алгебрах существуют двойственные утверждения, они либо одновременно верны, либо одновременно неверны. Именно, если в формуле, которая верна в некоторой булевой алгебре, поменять все конъюнкции на дизъюнкции, 0 на 1, ≤ на ≥ и наоборот, то получится формула, также истинная в этой булевой алгебре. Это следует из симметричности аксиом относительно таких замен.

Представления булевых алгебр

Можно доказать, что любая конечная булева алгебра изоморфна булевой алгебре всех подмножеств какого-то множества. Отсюда следует, что количество элементов в любой конечной булевой алгебре будет степенью двойки.

Знаменитая теорема Стоуна утверждает, что любая булева алгебра изоморфна булевой алгебре всех открыто-замкнутых множеств какого-то компактного вполне несвязного хаусдорфова топологического пространства.

Аксиоматизация

В 1933 г. американский математик Хантингтон предложил следующую аксиоматизацию для булевых алгебр:

Здесь использованы обозначения Хантингтона: + означает дизъюнкцию, n — отрицание.

Герберт Роббинс поставил следующий вопрос: можно ли сократить последнюю аксиому так, как написано ниже, то есть будет ли определённая выписанными ниже аксиомами структура булевой алгеброй?

Аксиоматизация алгебры Роббинса:

Этот вопрос оставался открытым с 30-х годов и был любимым вопросом Тарского и его учеников.

См. также

ast:Álxebra de Boole bg:Булева алгебра bn:বুলিয়ান বীজগণিত ca:Àlgebra de Boole cs:Booleova algebra eo:Bulea algebro fa:جبر بولی gl:Álxebra de Boole he:אלגברה בוליאנית hr:Booleova algebra hu:Boole-algebra id:Aljabar Boolean io:Booleana algebro lt:Būlio algebra nl:Booleaanse algebra no:Boolsk algebra pl:Algebra Boole’a simple:Boolean algebra sl:Booleova algebra sr:Булова алгебра sv:Boolesk algebra th:พีชคณิตแบบบูล tl:Aldyebrang Boolean uk:Булева алгебра

Источник