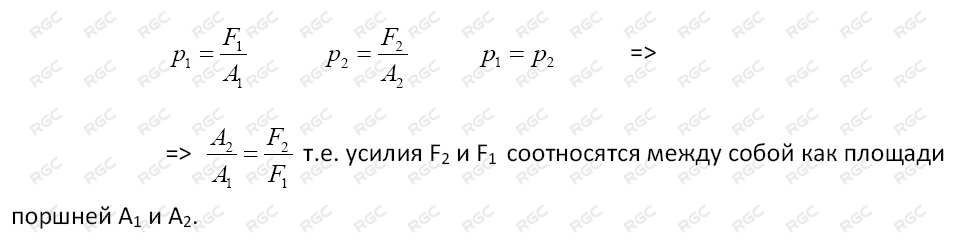Что такое давление гидравлика

Понятие гидростатического давления

В гидравлике есть несколько ключевых понятий. Центральное место отводится понятию гидростатического давления жидкости. Оно тесно связано с понятием напора жидкости, о котором будет сказано чуть позже.

Что такое

Одно из широко распространенных определений гидростатического давления звучит так: «Гидростатическое давление в точке жидкости – это нормальное сжимающее напряжение, возникающее в покоящейся жидкости под действием поверхностных и массовых сил».

Напряжение – это понятие, широко используемое в курсе сопротивления материалов. Идея в следующем. В физике, мы знаем, есть понятие силы. Сила – векторная величина, характеризующая воздействие. Векторная – это значит, что представляется в виде вектора, т.е. стрелки в трехмерном пространстве. Эта сила может быть приложена в отдельной точке (сосредоточенная сила), или к поверхности (поверхностная), или ко всему телу (говорят, массовая / объемная). Поверхностные и массовые силы являются распределенными. Только такие и могут действовать на жидкость, так как она обладает функцией текучести (легко деформируется от любого воздействия).

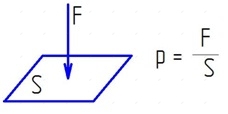
Сила приложена к поверхности с какой-то конкретной площадью. В каждой точке этой поверхности возникнет напряжение, равное отношению силы к площади, это и есть понятие давления в физике.

В чем измеряется

В системе СИ единица измерения силы – Ньютон [Н], площади – квадратный метр [м 2 ].

Отношение силы к площади: 1 Н / 1 м 2 = 1 Па (Паскаль).

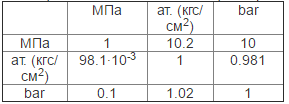
Паскаль является основной единицей измерения давления, но далеко не единственной. Ниже представлен пересчет единиц измерения давлений из одной в другую

100 000 Па = 0,1 МПа = 100 кПа ≈ 1 атм = 1 бар = 1 кгс/см 2 = 14,5 psi ≈ 750 мм.рт.ст ≡ 750 Торр ≈ 10 м.вод.ст (м)

Шкала и виды давлений

Далее, принципиально важным моментом является так называемая шкала давлений или виды давлений. На рисунке ниже представлено, как взаимоувязаны такие понятия как абсолютное давление, абсолютный вакуум, частичный вакуум, избыточное или манометрическое давление.

Абсолютное давление – давление, отсчитываемое от нуля.

Абсолютный вакуум – ситуация, при которой на рассматриваемую точку ничего не действует, т.е. давление, равное 0 Па.

Атмосферное давление – давление, равное 1 атмосфере. Отношение веса (mg) вышележащего столба воздуха к площади его поперечного сечения. Атмосферное давление зависит от места, времени суток. Это один из параметров погоды. В прикладных инженерных дисциплинах обычно все отсчитывают именно от атмосферного давления, а не от абсолютного вакуума.

Частичный вакуум (или еще часто говорят – «величина вакуума», « разрежение» или «отрицательное избыточное давление» ). Частичный вакуум – недостаток давления до атмосферного. Максимально возможная на Земле величина вакуума как раз равняется одной атмосфере (

10 м.вод.ст.). Это означает, что у вас не получится попить воду через трубочку с расстояния 11 м при всем желании.

* на самом деле при нормальном для трубочек для напитков диаметре (

5-6 мм) эта величина будет гораздо меньше из-за гидравлических сопротивлений. Но даже через толстый шланг вы не сможете попить воду с глубины 11 м.

Если заменить вас на насос, а трубочку – на его всасывающий трубопровод, то ситуация принципиально не изменится. Поэтому воду из скважин добывают как правило именно скважинными насосами, которые опускаются непосредственно в воду, а не пытаются засасывать воду с поверхности земли.

Избыточное давление (или также еще называемое манометрическим)– превышение давления над атмосферным.

Приведем следующий пример. На данной фотографии показано измерение давления в автомобильной шине при помощи прибора манометра.

Манометр показывает именно избыточное давление. На этой фотографии видно, что избыточное давление в данной шине приблизительно 1,9 бар, т.е. 1,9 атм, т.е. 190 000 Па. Тогда абсолютное давление в этой шине – 290 000 Па. Если мы шину проткнем, то воздух начнет под разницей давлений выходить наружу до тех пор, пока давление внутри и снаружи шины не станет одинаковым, атмосферным. Тогда избыточное давление в шине будет равно 0.

Формула расчета давления в открытом сосуде

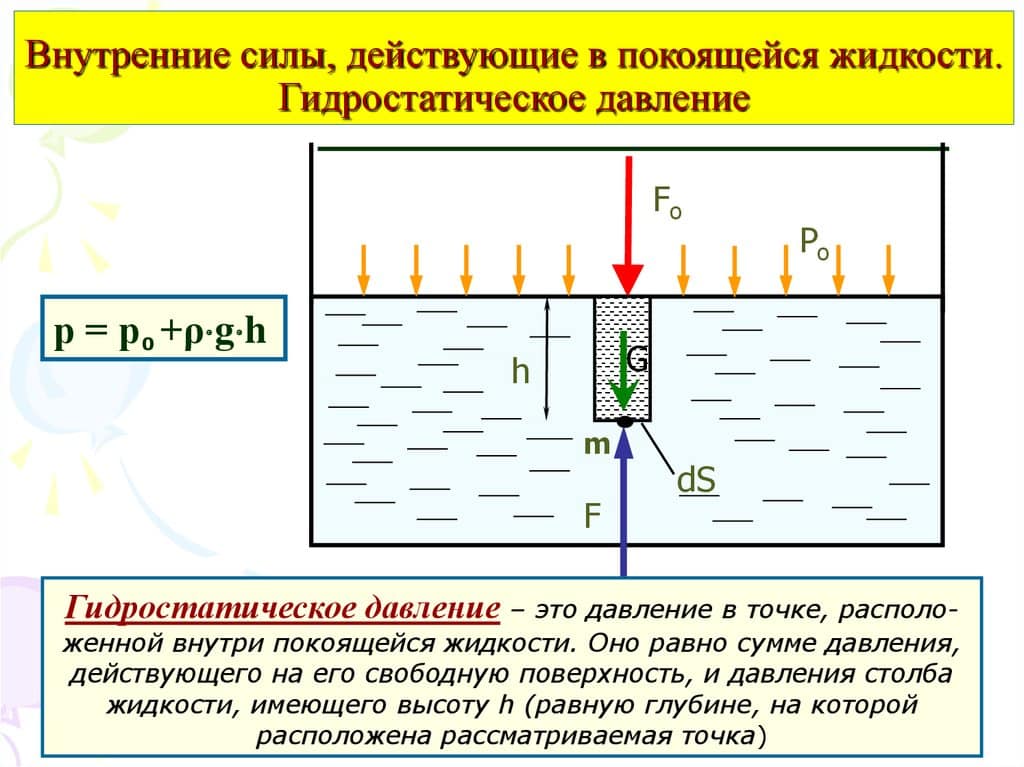
Теперь посмотрим, как определить гидростатическое давление в жидкости, находящейся в определенном объеме. Допустим, мы рассматриваем открытую бочку с водой.

На поверхности воды в бочке устанавливается атмосферное давление (обозначено маленькой буквой p с индексом «атм»). Соответственно, избыточное давление жидкости на поверхности равняется 0 Па. Теперь рассмотрим гидростатическое давление в точке X. Эта точка заглублена относительно поверхности воды на расстояние h, и за счет столба жидкости, гидростатическое давление в ней будет больше, чем на поверхности.

Давление в точке X (p_x) будет определяться, как давление на поверхности + давление, создаваемое столбом жидкости. Это называется основным уравнением гидростатики.

При глубине h 2 м, абсолютное гидростатическое давление составит:

100 000 Па + 1000·10·2 Па = 100 000 Па +20 000 Па = 120 000 Па = 1,2 атм.

Избыточное давление жидкости – это значит за вычетом атмосферного: 120 000 – 100 000 = 20000 Па = 0,2 атм.

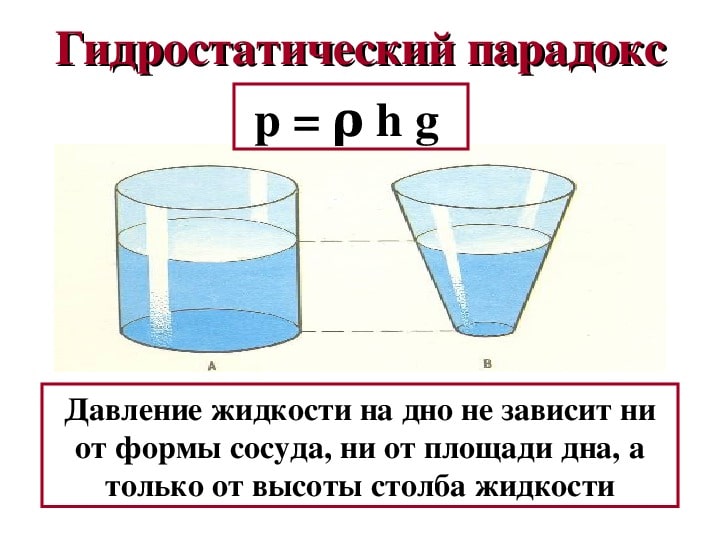
Таким образом, в избыточное давление в точке X определяется высотой столба жидкости. Форма емкости при этом никак не влияет. Если мы рассмотрим гигантский бассейн с глубиной 2 м, и трубку высотой 3 м, то гидростатическое давление на дне трубки будет больше, нежели на дне бассейна.

(Абсолютное гидростатическое давление на дне бассейна: 100000 + 1000*9,81*2 =

Высота столба жидкости определяет давление, создаваемое этим столбом жидкости.p_изб = ρgh.

Таким образом, гидростатическое давление можно выражать единицами длины (высоты): h = p / ρg

Например, рассмотрим, какое давление создает столб ртути высотой 750 мм:

p = ρgh = 13600 · 10 · 0,75 = 102 000 Па ≈ 100 000 Па, что отсылает нас к единицам измерения давления, рассмотренным ранее.

Т.е. 750 мм.рт.ст. = 100 000 Па.

По тому же принципу получается, что давление в 10 метров водяного столба равняется 100 000 Па:

1000 · 10 · 10 = 100 000 Па.

Выражение гидростатического давления в метрах водяного столба принципиально важно для водоснабжения, водоотведения, а также гидравлических расчетов отопления, гидротехнических расчетов и т. д.

Давление жидкости в трубах и его нормативы

Теперь посмотрим гидростатическое давление жидкости в трубопроводах. Что физически означает замеренное мастером давление в определенной точке (X) трубопровода? Манометр в данном случае показывает 2 кгс/см² (2 атм). Это избыточное давление в трубопроводе, оно эквивалентно 20 метрам водяного столба. Иными словами, если подсоединить к трубе вертикальную трубку, то вода в ней поднимется на величину избыточного давления, т.е. на высоту 20 м. Вертикальная трубка, которая сообщается с атмосферой (т.е. открытая) называются пьезометром.

Основная задача системы водоснабжения заключается в том, чтобы в требуемой точке вода имела необходимое избыточное давление. Например, согласно нормативному документу:

[ Постановление Правительства РФ от 06.05.2011 N 354 (ред. от 13.07.2019) «О предоставлении коммунальных услуг собственникам и пользователям помещений в многоквартирных домах и жилых домов» (вместе с «Правилами предоставления коммунальных услуг собственникам и пользователям помещений в многоквартирных домах и жилых домов») ] >>> давление в точке водоразбора должно быть не менее 3 м.вод.ст (0,03 МПа)

Однако необходимо отметить, что нормативно допустимая величина в 3 м.вод.ст – это совсем не много, так как современное сантехническое оборудование может требовать гидростатическое давление жидкости до 13 м.вод.ст в месте подключения для нормальной работы (подачи достаточного количества воды). Например, даже в старом СНиП по внутреннему водопроводу (СНиП 2.04.01-85*), указано, что при использовании аэратора на смесителе (сеточка, перекрывающая выходное отверстие), в точке подключения смесителя необходимо давление 5 м.вод.ст.

Распределение давления жидкости в тубах

Источник

Гидростатическое давление: формула, свойства и особенности

Понимание законов и свойств гидростатического давления необходимо при создании и применении оборудования, работающего на гидроавтоматике, насосов любых видов, типов.

Оглавление:

Если заглянем в словарь или «Википедию», выясним, что гидростатическое давление — это давление силы тяжести на жидкость. Занимается гидростатикой один из разделов гидравлики, где изучаются законы равновесия жидкостей и оцениваются возможности применения этих законов на практике.

Самое важное о гидростатическом давлении: закон Паскаля и формула

Закон гидростатики был открыт Паскалем в 1653 году. Звучит закон так: давление на поверхность жидкости, которое передается внешними силами, передается в жидкости во всех направлениях одинаково. Другими словами, давление на жидкость передается не только в направлении действия силы, но и равнозначно во все другие направления.

Этот закон оказался весьма полезным и нашел широкое применение в промышленности. На законе Паскаля основана работа гидроавтоматики, которая управляет автомобилями, станками с ЧПУ, самолетами, другими гидравлическими машинами.

Формула гидростатического давления выглядит так:

p – плотность жидкости,

g – ускорение свободного падения, постоянная величина,

h – глубина, где необходимо определить давление.

Важно: величина гидростатического давления не зависит от формы сосуда, где находится жидкость.

Особенности измерения гидростатического давления и его свойства

Учет величины гидростатического давления может вестись разными способами. Если необходимо рассчитать полное или абсолютное гидростатическое давление, учитывающее атмосферное давление, действующее на поверхность жидкости, величина измеряется в абсолютных технических атмосферах. Но часто атмосферное давление на свободной поверхности не учитывают, определяя манометрическое или избыточное гидростатическое давление — то, которое действует сверх атмосферного. Чтобы найти манометрическое давление, нужно из абсолютного вычесть атмосферное. Измеряет ся избыточное давление также в технических атмосферах, но уже избыточных.

1. Гидростатическое давление воды всегда направлено к площади, на которую воздействует, по внутренней нормали. Это свойство обусловлено тем, что в покоящейся жидкости нет растягивающих и касательных усилий. И отсюда следует вывод: при изменении давления в определенной точке следует ожидать такого же изменения в любой другой точке жидкости.

2. В конкретной точке величина давления не зависит от направления — оно одинаково по всем направлениям. Другими словами, внешнее давление на свободную поверхность жидкости передается во все точки без изменений.

3. На величину давления влияет вязкость жидкости. Вязкость — свойство жидкости сопротивляться перемещению одной ее части относительно другой. Это свойство проявляется только во время движения, колебания жидкости и распределяет скорости по живому сечению потока.

Несколько слов о кавитационном режиме насосов

При достижении определенных условий в насосах может возникать кавитация — явление, которое создается при снижении гидростатического давления и характеризуется появлением пузырьков газа в движущейся жидкости. В зоне, где гидростатическое давление повышается, пузырьки схлопываются.

Сегодня не существует материалов, которые имели бы абсолютную устойчивость к кавитационным разрушениям, поэтому нельзя допускать работу насосов в кавитационном режиме. Основное средство по предупреждению кавитации — регулирование давления во всасывающем трубопроводе. Оптимальные параметры определяются высотой всасывания жидкости во время функционирования насоса.

Чтобы определить критический кавитационный запас, при производстве насоса проводят кавитационные испытания. В результате каждый режим работы насосного оборудования получает кавитационную характеристику, определяемую зависимостью мощности и напора насоса от кавитационного запаса.

Источник

Основные понятия и принципы гидравлики

Основные понятия и принципы.

Введение.

Данный цикл статей рассчитан на широкий круг эксплуатантов гидравлического оборудования с различным уровнем теоретической подготовки в области гидравлики. Данный цикл статей не является полным и исчерпывающим, а несет некоторые базовые сведения о физических принципах работы гидросистем и гидравлических агрегатах. Статьи содержат в себе обзорную информацию с акцентом на вопросы, наиболее часто вызывающие затруднения у наших клиентов.

Гидравлика в наши дни прочно укоренилась в различных машинах и механизмах. Гидросистемы нашли широкое распространение в станочной технике, манипуляторах, подъемных устройствах, дорожной технике, автотранспорте, в механизмах летательных аппаратов, водного транспорта и т.д. Повсеместное применение гидравлических систем взамен систем механических приводов обусловлено прежде всего простотой преобразования вращательного движения гидронасоса в поступательное (линейное) или вращательное движение исполнительного гидродвигателя. При правильном подборе гидронасоса и исполнительного гидродвигателя можно получить практически любое усилие. Также преимуществом гидропривода является его компактность, малые размеры гидроагрегатов – следствие высокой удельной мощности. На рис.1 представлен электрический генератор мощностью 50 кВт и приводящий его гидромотор той-же мощности. Наглядно видно что гидромотор имеет заметно меньшие размеры при равной мощности.

Рассмотрим основные понятия и принципы гидравлики.

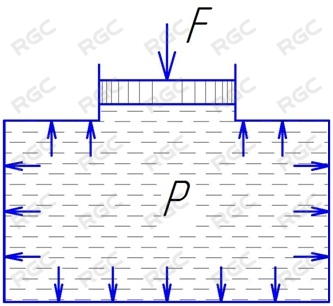
Понятие давления.

Давление это величина численно равная значению действию силы на единицу площади см. рис.2

Упрощенно данную зависимость можно представить аналогично закону Ома в электротехнике:

Основная единица измерения давления – Паскаль [Па]

Таблица 1. Соотношения единиц измерения давления.

Гидростатическое давление – давление покоящегося столба жидкости.

Внутри столба жидкости под тяжестью массы жидкости, действующей на определенную площадь возникает давление, которое зависит от высоты столба жидкости (h), плотности жидкости (ρ) и ускорения свободного падения (g).

P= ρ ∙g∙h

Если рассматривать различные формы сосудов, наполненных одной и той-же жидкостью то давление в определенной точке будет зависеть только от высоты столба жидкости. Р1=P2=P3 см. рис. 3.

Закон Паскаля

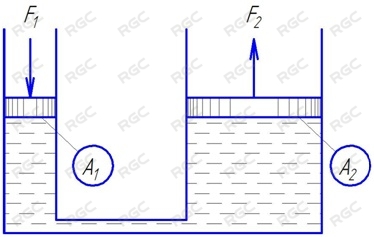
Одним из основных законов гидравлики является закон Паскаля. Он гласит что давление в замкнутом сосуде вызванное действием внешней силы равномерно распределяется во всех направлениях и одинаково в любой точке. (в данном законе не учитывается гидростатическое давление т.к. оно ничтожно мало по сравнению с значениями давлений действующими в гидросистемах). См рис.4.

Закон Паскаля лежит в основе принципа передачи усилия посредством гидравлики. Рис.5.

Как следует из закона Паскаля давление во всех точках рабочей жидкости одинаково, следовательно:

В качестве простого примера применения данного принципа может служить обычный гидравлический домкрат.

Заключение

В данной статье описаны основные принципы используемые в системах гидростатического привода. На основе этих законов построены практически все гидросистемы станочных приводов и мобильных машин. Владея всего несколькими законами гидравлики, читатель сможет выполнить силовой расчет исполнительного гидроцилиндра и оценить преимущества применения гидропривода.

Внимание! Данная статья авторская. При копировании ее с сайта обязательно указывать источник!

Источник

Гидравлика

Информативные ответы на все вопросы курса «Гидравлика» в соответствии с Государственным образовательным стандартом.

Оглавление

Приведённый ознакомительный фрагмент книги Гидравлика предоставлен нашим книжным партнёром — компанией ЛитРес.

4. Гидростатическое давление и его свойства

Общие дифференциальные уравнения равновесия жидкости — уравнения Л. Эйлера для гидростатики.

Если взять цилиндр с жидкостью (покоящейся) и провести через него линию раздела, то получим жидкость в цилиндре из двух частей. Если теперь приложить некоторое усилие к одной части, то оно будет передаваться другой через разделяющую плоскость сечения цилиндра: обозначим эту плоскость S = w.

Если саму силу обозначить как то взаимодействие, передаваемое от одной части к другой через сечение Δw, и есть гидростатическое давление.

Если оценить среднее значение этой силы,

Рассмотрев точку А как предельный случай w, определяем:

Если перейти к пределу, то Δw переходит в точку А.

Мы доказали, что во всех трех направлениях (их мы выбрали произвольно) скалярное значение сил одно и то же, то есть не зависит от ориентации сечения Δw.

Вот это скалярное значение приложенных сил и есть гидростатическое давление, о котором говорили выше: именно это значение, сумма всех составляющих, передается через Δw.

Другое дело, что в сумме (p_x + p_y + p_z) какая-то составляющая окажется равной нулю.

Как мы в дальнейшем убедимся, в определенных условиях гидростатическое давление все же может быть неодинаково в различных точках одной и той же покоящейся жидкости, т. е.

Свойства гидростатического давления.

1. Гидростатическое давление всегда направлено по нормали к поверхности и его величина не зависит от ориентации поверхности.

2. Внутри покоящейся жидкости в любой точке гидростатическое давление направлено по внутренней нормали к площадке, проходящей через эту точку.

3. Для любых двух точек одного и того же объема однородной несжимаемой жидкости (ρ = const)

где ρ — плотность жидкости;

П₁, П₂ — значение поле массовых сил в этих точках.

Поверхность, для любых двух точек которой давление одно и то же, называется поверхностью равного давления.

Источник

Что такое давление гидравлика

Гидравлика делится на два раздела: гидростатика и гидродинамика. Гидродинамика является более обширным разделом и будет рассмотрена в последующих лекциях. В этой лекции будет рассмотрена гидростатика.

Гидростатикой называется раздел гидравлики, в котором рассматриваются законы равновесия жидкости и их практическое применение.

В покоящейся жидкости всегда присутствует сила давления, которая называется гидростатическим давлением. Жидкость оказывает силовое воздействие на дно и стенки сосуда. Частицы жидкости, расположенные в верхних слоях водоема, испытывают меньшие силы сжатия, чем частицы жидкости, находящиеся у дна.

Рассмотрим резервуар с плоскими вертикальными стенками, наполненный жидкостью (рис.2.1, а). На дно резервуара действует сила P равная весу налитой жидкости G = γ V, т.е. P = G.

Если эту силу P разделить на площадь дна S_abcd, то мы получим среднее гидростатическое давление, действующее на дно резервуара.

Гидростатическое давление обладает свойствами.

Свойство 1. В любой точке жидкости гидростатическое давление перпендикулярно площадке касательной к выделенному объему и действует внутрь рассматриваемого объема жидкости.

Для доказательства этого утверждения вернемся к рис.2.1, а. Выделим на боковой стенке резервуара площадку S_бок (заштриховано). Гидростатическое давление действует на эту площадку в виде распределенной силы, которую можно заменить одной равнодействующей, которую обозначим P. Предположим, что равнодействующая гидростатического давления P, действующая на эту площадку, приложена в точке А и направлена к ней под углом φ (на рис. 2.1 обозначена штриховым отрезком со стрелкой). Тогда сила реакции стенки R на жидкость будет иметь ту же самую величину, но противоположное направление (сплошной отрезок со стрелкой). Указанный вектор R можно разложить на два составляющих вектора: нормальный R_n (перпендикулярный к заштрихованной площадке) и касательныйR_τ к стенке.

Сила нормального давления R_n вызывает в жидкости напряжения сжатия. Этим напряжениям жидкость легко противостоит. Сила R_τ действующая на жидкость вдоль стенки, должна была бы вызвать в жидкости касательные напряжения вдоль стенки и частицы должны были бы перемещаться вниз. Но так как жидкость в резервуаре находится в состоянии покоя, то составляющая R_τ отсутствует. Отсюда можно сделать вывод первого свойства гидростатического давления.

Свойство 2. Гидростатическое давление неизменно во всех направлениях.

В жидкости, заполняющей какой-то резервуар, выделим элементарный кубик с очень малыми сторонами Δx, Δy, Δz (рис.2.1, б). На каждую из боковых поверхностей будет давить сила гидростатического давления, равная произведению соответствующего давления P_x, P_y , P_z на элементарные площади. Обозначим вектора давлений, действующие в положительном направлении (согласно указанным координатам) как P’_x, P’_y, P’_z, а вектора давлений, действующие в обратном направлении соответственно P»_x, P»_y, P»_z. Поскольку кубик находится в равновесии, то можно записать равенства

Сократив полученные равенства, найдем, что

Членом третьего уравнения γΔz, как бесконечно малым по сравнению с P’_z и P»_z, можно пренебречь и тогда окончательно

Вследствие того, что кубик не деформируется (не вытягивается вдоль одной из осей), надо полагать, что давления по различным осям одинаковы, т.е.

Это доказывает второй свойство гидростатического давления.

Свойство 3. Гидростатическое давление в точке зависит от ее координат в пространстве.

Это положение не требует специального доказательства, так как ясно, что по мере увеличения погружения точки давление в ней будет возрастать, а по мере уменьшения погружения уменьшаться. Третье свойство гидростатического давления может быть записано в виде

Пусть жидкость содержится в сосуде (рис.2.2) и на ее свободную поверхность действует давление P₀ . Найдем гидростатическое давление P в произвольно взятой точке М, расположенной на глубине h. Выделим около точки М элементарную горизонтальную площадку dS и построим на ней вертикальный цилиндрический объем жидкости высотой h. Рассмотрим условие равновесия указанного объема жидкости, выделенного из общей массы жидкости. Давление жидкости на нижнее основание цилиндра теперь будет внешним и направлено по нормали внутрь объема, т.е. вверх.

Запишем сумму сил, действующих на рассматриваемый объем в проекции на вертикальную ось:

Последний член уравнения представляет собой вес жидкости, заключенный в рассматриваемом вертикальном цилиндре объемом hdS. Силы давления по боковой поверхности цилиндра в уравнение не входят, т.к. они перпендикулярны к этой поверхности и их проекции на вертикальную ось равны нулю. Сократив выражение на dS и перегруппировав члены, найдем

Полученное уравнение называют основным уравнением гидростатики. По нему можно посчитать давление в любой точке покоящейся жидкости. Это давление, как видно из уравнения, складывается из двух величин: давления P₀ на внешней поверхности жидкости и давления, обусловленного весом вышележащих слоев жидкости.

Из основного уравнения гидростатики видно, что какую бы точку в объеме всего сосуда мы не взяли, на нее всегда будет действовать давление, приложенное к внешней поверхности P₀. Другими словами давление, приложенное к внешней поверхности жидкости, передается всем точкам этой жидкости по всем направлениям одинаково. Это положение известно под названием закона Паскаля.

Поверхность, во всех точках которой давление одинаково, называется поверхностью уровня (подробно рассмотрим в п.2.6). В обычных условиях поверхности уровня представляют собой горизонтальные плоскости.

Пусть мы имеем резервуар с наклонной правой стенкой, заполненный жидкостью с удельным весом γ. Ширина стенки в направлении, перпендикулярном плоскости чертежа (от читателя), равна b (рис.2.3). Стенка условно показана развернутой относительно оси АВ и заштрихована на рисунке. Построим график изменения избыточного гидростатического давления на стенку АВ.

Так как избыточное гидростатическое давление изменяется по линейному закон P=γgh, то для построения графика, называемого эпюрой давления, достаточно найти давление в двух точках, например А и B.

Избыточное гидростатическое давление в точке А будет равно

Соответственно давление в точке В:

Согласно первому свойству гидростатического давления, оно всегда направлено по нормали к ограждающей поверхности. Следовательно, гидростатическое давление в точке В, величина которого равна γH, надо направлять перпендикулярно к стенке АВ. Соединив точку А с концом отрезка γH, получим треугольную эпюру распределения давления АВС с прямым углом в точке В. Среднее значение давления будет равно

Если площадь наклонной стенки S=bL, то равнодействующая гидростатического давления равна

Однако точка приложения равнодействующей гидростатического давления ц.д. не всегда будет совпадать с центром тяжести плоской поверхности. Эта точка находится на расстоянии l от центра тяжести и равна отношению момента инерции площадки относительно центральной оси к статическому моменту этой же площадки.

В частном случае, когда стенка имеет форму прямоугольника размерами bL и одна из его сторон лежит на свободной поверхности с атмосферным давлением, центр давления ц.д. находится на расстоянии b/3 от нижней стороны.

Пусть жидкость заполняет резервуар, правая стенка которого представляет собой цилиндрическую криволинейную поверхность АВС (рис.2.4), простирающуюся в направлении читателя на ширину b. Восстановим из точки А перпендикуляр АО к свободной поверхности жидкости. Объем жидкости в отсекеАОСВ находится в равновесии. Это значит, что силы, действующие на поверхности выделенного объема V, и силы веса взаимно уравновешиваются.

Представим, что выделенный объем V представляет собой твердое тело того же удельного веса, что и жидкость (этот объем на рис.2.4 заштрихован). Левая поверхность этого объема (на чертеже вертикальная стенка АО) имеет площадь Sx = bH, являющуюся проекцией криволинейной поверхности АВС на плоскостьyOz.

С правой стороны на отсек будет действовать реакция R цилиндрической поверхности. Пусть точка приложения и направление этой реакции будут таковы, как показано на рис.2.4. Реакцию R разложим на две составляющие R_x и R_z.

Из действующих поверхностных сил осталось учесть только давление на свободной поверхности Р₀. Если резервуар открыт, то естественно, что давление Р₀ одинаково со всех сторон и поэтому взаимно уравновешивается.

На отсек АВСО будет действовать сила собственного веса G = γV, направленная вниз.

Спроецируем все силы на ось Ох:

Теперь спроецируем все силы на ось Оz:

Составляющая силы гидростатического давления по оси O_y обращается в нуль, значит R_y = F_y = 0.

Таким образом, реакция цилиндрической поверхности в общем случае равна

а поскольку реакция цилиндрической поверхности равна равнодействующей гидростатического давленияR=F, то делаем вывод, что

Тело, погруженное (полностью или частично) в жидкость, испытывает со стороны жидкости суммарное давление, направленное снизу вверх и равное весу жидкости в объеме погруженной части тела.

Для однородного тела плавающего на поверхности справедливо соотношение

Существующая теория плавающего тела довольно обширна, поэтому мы ограничимся рассмотрением лишь гидравлической сущности этой теории.

Теперь рассмотрим условия равновесия судна:

1) если h > 0, то судно возвращается в первоначальное положение;
2) если h = 0, то это случай безразличного равновесия;
3) если h

Следовательно, чем ниже расположен центр тяжести и, чем больше метацентрическая высота, тем больше будет остойчивость судна.

Как уже отмечалось выше, поверхность, во всех точках которой давление одинаково, называетсяповерхностью уровня или поверхностью равного давления. При неравномерном или непрямолинейном движении на частицы жидкости кроме силы тяжести действуют еще и силы инерции, причем если они постоянны по времени, то жидкость принимает новое положение равновесия. Такое равновесие жидкости называется относительным покоем.

Рассмотрим два примера такого относительного покоя.

В первом примере определим поверхности уровня в жидкости, находящейся в цистерне, в то время как цистерна движется по горизонтальному пути с постоянным ускорением a (рис.2.6).

К каждой частице жидкости массы m должны быть в этом случае приложены ее вес G = mg и сила инерцииP_u, равная по величине ma. Равнодействующая этих сил направлена к вертикали под углом α, тангенс которого равен

Так как свободная поверхность, как поверхность равного давления, должна быть нормальна к указанной равнодействующей, то она в данном случае представит собой уже не горизонтальную плоскость, а наклонную, составляющую угол α с горизонтом. Учитывая, что величина этого угла зависит только от ускорений, приходим к выводу, что положение свободной поверхности не будет зависеть от рода находящейся в цистерне жидкости. Любая другая поверхность уровня в жидкости также будет плоскостью, наклоненной к горизонту под углом α. Если бы движение цистерны было не равноускоренным, а равнозамедленным, направление ускорения изменилось бы на обратное, и наклон свободной поверхности обратился бы в другую сторону (см. рис.2.6, пунктир).

Поверхность жидкости также должна быть нормальна в каждой точке к равнодействующей этих сил R и представит собой параболоид вращения. Из чертежа находим

или после интегрирования

В точке пересечения кривой АОВ с осью вращения r = 0, z = h = C, поэтому окончательно будем иметь

т.е. кривая АОВ является параболой, а свободная поверхность жидкости параболоидом. Такую же форму имеют и другие поверхности уровня.

Для определения закона изменения давления во вращающейся жидкости в функции радиуса и высоты выделим вертикальный цилиндрический объем жидкости с основанием в виде элементарной горизонтальной площадки dS (точка М) на произвольном радиусе r и высоте z и запишем условие его равновесия в вертикальном направлении. С учетом уравнения (2.11) будем иметь

После сокращений получим

Это значит, что давление возрастает пропорционально радиусу r и уменьшается пропорционально высоте z.

Источник