Что такое деление числа в данном отношении

Математика. 6 класс

Конспект урока

Деление числа в данном отношении

Перечень вопросов, рассматриваемых в теме:

Частное двух не равных нулю чисел a и b называется отношением чисел a и b.

Числа a и b называются членами отношения.

Скорость – это отношение пройденного пути ко времени, за которое этот путь пройден.

Скорость сближения – это расстояние, на которое сближаются объекты за единицу времени.

Цена товара – это отношение стоимости товара к его массе или количеству единиц товара.

Теоретический материал для самостоятельного изучения

Сегодня мы с вами разберём, что означает деление числа в данном отношении.

Правило деления числа в данном отношении.

Чтобы разделить число c в отношении a к b, можно разделить число c на сумму членов отношения a + b и результат умножить на каждый член отношения, числа a, b и c не равны нулю.

Ответ: конфеты между друзьями надо разделить так: первому – 16 конфет, а второму – 64 конфеты.

Сестра и брат сложили свои деньги для покупки лотерейного билета. У сестры было 50 рублей, а у брата 30 рублей. Билет выиграл 4000 рублей. Как они должны разделить эти деньги между собой?

Ответ: 2500 рублей, 1500 рублей.

Трое хотят купить фирму по продаже мороженого. Первый желает иметь 6 частей акций, второй – 4 части акций, третий – 2 части. Всего нужно заплатить 960 000 рублей. Сколько денег должен внести каждый из них.

Ответ: 480 000 рублей, 320 000 рублей, 160 000 рублей.

Первая машинистка печатает 180 страниц за 20 часов, а вторая – за 30 часов. Как распределить между ними 180 страниц, чтобы они напечатали их в кратчайший срок?

Ответ: первой машинистке – 108 страниц, второй – 72 страницы.

Мотоциклист может проехать расстояние между пунктами за 4 часа, а велосипедист – за 12 часов. Однажды они одновременно отправились навстречу друг другу из этих пунктов. Сколько километров проедет каждый до встречи, если расстояние между пунктами 120 километров?

Разбор решения заданий тренировочного модуля

№1. Тип задания: сортировка элементов по категориям.

Поставьте в соответствующие столбцы числа, которые можно разделить нацело в заданных отношениях.

№2. Тип задания: подчеркивания.

Нужно подчеркнуть правильный вариант ответа.

Источник

Деление числа в данном отношении

Урок 23. Математика 6 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Деление числа в данном отношении»

Представим себе такую историю…

– Саша, чем ты занимаешься? – поинтересовался у друга Паша.

– Хочу приготовить мороженое, – ответил Саша. – Уже и рецепт нашёл, и подготовил все ингредиенты, но вот только разобраться не могу, сколько чего брать.

– А что в рецепте написано? – уточнил Паша.

– В рецепте сказано, что для приготовления мороженого нужно смешать 3 части молока, 2 части сливок и 1 часть сахара, – прочитал Саша. – А как эти части высчитать, если я хочу приготовить, например, 3 килограмма мороженого?

– И вправду, сложная задача у тебя получается, – задумался Паша. – Как эти части считать, не понятно. Но я знаю, кто нам сможет помочь!

– Ребята, прежде чем я отвечу на ваш вопрос, давайте немного разомнёмся и выполним устные задания, – предложил Мудряш.

– Давайте сверимся! – сказал Мудряш. — Посмотрите, что у вас должно было получиться!

– Ну а теперь вернёмся к вашему вопросу, – начал Мудряш. – Чтобы ответить на вопрос «Сколько каких ингредиентов нужно взять для приготовления смеси мороженого?», прежде всего нужно научиться выполнять деление числа в данном отношении. Итак, вы хотите приготовить 3 килограмма мороженого. Для удобства давайте переведём килограммы в граммы, всё же так будет легче и привычнее считать.

– Так как 1 килограмм равен 1000 грамм, – стал размышлять Саша, – значит, я хочу приготовить 3000 грамм мороженого.

– Хорошо! – согласился Мудряш. – По рецепту для приготовления мороженого нужно смешать 3 части молока, 2 части сливок и 1 часть сахара. Будем считать, что смесь мороженого состоит из 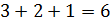частей, имеющих одинаковые массы. Тогда как посчитать, сколько приходится на 1 часть?

– Нужно 3000 разделить на 6, – ответил Паша.

– Правильно! – сказал Мудряш. – Значит, масса одной части смеси равна 500 граммам. По рецепту молоко в смеси составляет 3 части, сливки – 2 части, а сахар – 1 часть. Посчитайте, чему же будут равны эти части.

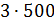
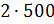
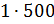
– Тогда масса молока в смеси будет равна и равна 1500 граммам, – принялся считать Саша. – Масса сливок будет равна и равна 1000 грамм, а масса сахара будет равна и равна 500 граммам.

– Получается, что для приготовления 3 килограммов мороженого нужно взять 1500 грамм молока, добавить 1000 грамм сливок, а затем добавить 500 грамм сахара? – решил уточнить Паша.

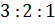
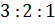
– Всё верно! – согласился Мудряш. – Из решения вашей задачи следует, что число 3000 можно представить в виде суммы трёх слагаемых – 1500, 1000 и 500, отношение которых равно . В таких случаях говорят, что число 3000 разделили в отношении . Также можно сказать, что число 3000 представили в виде суммы трёх слагаемых, пропорциональных числам 3, 2 и 1.

– И совсем несложная задача оказалась, – заметил Саша. – Теперь я без труда могу приготовить мороженое.

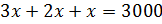
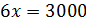
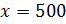
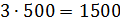
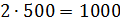
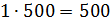
– Эту же задачу можно было решить и другим способом, – продолжил Мудряш. – Пусть масса одной части смеси мороженого составляет х грамм. Тогда массы молока, сливок и сахара составляют соответственно 3х грамм, 2х грамм и х грамм. Поскольку масса всей смеси мороженого равна 3000 грамм, то можем составить уравнение . Решим это уравнение. Получим, что . Отсюда . Тогда массы молока, сливок и сахара равны соответственно грамм, грамм и грамм.

– Сделаем вывод, – сказал Мудряш. – Чтобы разделить число в данном отношении, можно разделить это число на сумму членов отношения, а затем результат умножить на каждый член отношения.

– А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним несколько заданий.

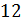
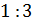
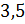
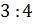
Задание первое: разделите числа в указанных отношениях: а) число в отношении ; б) число в отношении .

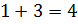
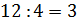
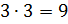
Решение: нужно разделить число 12 в отношении 1 к 3. Будем считать, что всё число состоит из частей. Значит, 1 часть равна . Тогда 3 части будут равны . Следовательно, число двенадцать можно разделить в отношении 1 к 3 так: 3 и 9.

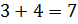
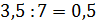
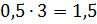
В следующем условии нам нужно разделить число 3,5 в отношении 3 к 4. Будем считать, что всё число состоит из частей. Тогда 1 часть равна . Отсюда 3 части числа равны . Следовательно, число 3,5 можно разделить в отношении 3 к 4 так: 1,5 и 2.

Следующее задание: два числа относятся как 4 к 7. Найдите эти числа, зная, что: их сумма равна 110, их разность равна 12.

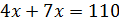
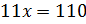
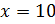
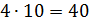
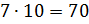
Решение: обозначим за х одну часть. Тогда можем записать, что первое число равно 4х, второе – 7х. В первом условии сказано, что сумма этих чисел равна 110. Составим уравнение . Решим его. Получим . Отсюда . Значит, первое число равно , второе – .

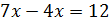
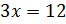
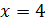
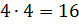
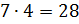
Во втором условии сказано, что разность этих чисел равна 12. Составим уравнение . Решим его. Получим . Отсюда . Значит, первое число равно , второе – .

Решим задачу: стороны прямоугольника 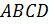относятся как 2 к 3. Найдите площадь этого прямоугольника, если его периметр равен 20 сантиметров.

И решим ещё одну задачу. Для приготовления фарфора смешивают 25 частей белой глины, 2 части песка и 1 часть гипса. Сколько нужно взять каждого материала, чтобы приготовить 504 грамма смеси?

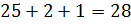
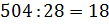
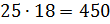
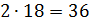
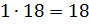
Решение: будем считать, что вся смесь состоит из частей, имеющих одинаковые массы. Тогда 1 часть содержит грамм. Следовательно, чтобы приготовить 504 грамма смеси фарфора, нужно взять: грамм белой глины, грамм песка и грамм гипса.

Источник

Деление числа в данном отношении

На практике и в курсе математики довольно часто приходится делить число (величину) в данном отношении. Такие задачи решают на ЕГЭ, решали и в глубокой древности. Начнём с задачи из Древнего Египта.

Задача 1. Число и его половина составляют 9. Найдите число.

Решение. Пусть половина числа составляет 1 часть, тогда само число — 2 такие же части, так как число в 2 раза больше своей половины.

1) 1 + 2 = 3 (части) — приходится на число и его половину,

2) 9: 3 = 3 (единицы) — приходится на 1 часть, это половина числа,

3) 3 * 2 = 6 (единиц) — приходится на число.

Изменим условие задачи на части — получим задачу на деление числа в данном отношении.

Задача 2. Разделите число 9 в отношении 2: 1. Найдите полученные числа.

Решение задачи записано выше. Сделаем вывод в виде правила, которому можно следовать при решении других задач, меняя число и члены отношения.

Чтобы число 9 разделить в отношении 2: 1, надо это число разделить на сумму членов отношения и результат умножить на каждый член отношения.

Запишем решение задачи по новому правилу.

Решение. 1) 9: (2 + 1) * 2 = 6 — большее число,

2) 9: (2 + 1) * 1 = 3 — меньшее число.

Разумеется, меньшее число можно было найти вычитанием: 9 — 6 = 3.

Задача 3. Брат и сестра разделили 35 конфет в отношении 3: 4. Брату досталась меньшая часть. Сколько конфет досталось сестре?

Решение. 1) 35: (3 + 4) * 3 = 15 (конфет) — досталось брату,

2) 35 — 15 = 20 (конфет) — досталось сестре.

Задача 4. Малыш и Карлсон разделили 16 плюшек в отношении 3: 5. Сколько плюшек досталось Карлсону, если Малышу досталось меньше плюшек?

Решение. 1) 16: (3 + 5) * 3 = 6 (плюшек) — досталось Малышу,

2) 16 — 6 = 10 (плюшек) — досталось Карлсону.

Задача для ребят постарше.

Задача 5. В треугольнике три стороны имеют длину 8, 10 и 12. На какие отрезки биссектриса треугольника делит среднюю его сторону?

Решение. Биссектриса треугольника делит его сторону на части, пропорциональные двум другим сторонам треугольника, то есть в отношении 8: 12 = 2: 3. Разделим сторону 10 в отношении 2: 3.

1) 10: (2 + 3) * 2 = 4 — длина меньшей части,

2) 10 — 4 = 6 — длина большей части.

На ЕГЭ базового уровня в 2018 году была такая задача.

Задача 6. Маша и Медведь съели 110 печений и банку варенья, начав и закончив одновременно. Сначала Маша ела варенье, а Медведь — печенье, но в какой-то момент они поменялись. Медведь и то, и другое ест в три раза быстрее Маши. Сколько печений съел Медведь, если варенья они съели поровну?

Решение. Так как варенья они съели поровну, а Медведь ест варенье в 3 раза быстрее Маши, то на варенье Медведь потратил времени в 3 раза меньше, чем Маша. Печенье Медведь ел в 3 раза больше времени, чем Маша, которая в это время ела варенье. Так как скорость поедания печенья у Медведя в 3 раза больше, чем у Маши, то Медведь съел печенья в 3*3 = 9 раз больше, чем Маша. Делим 110 печений в отношении 9: 1.Медведь съел 110: (9 + 1)*9 = 99 (печений).

Авторы комментариев ФИПИ к результатам ЕГЭ отметили, что в группе хорошо подготовленных к сдаче экзамена на базовом уровне решили эту задачу менее половины выпускников, включенных в эту группу. При этом предполагалось, что задачу будут решать составлением уравнения. Как показано выше, задачу можно решить и арифметически.

Источник

Деление числа в данном отношении + задачи с решением

В шестом классе изучается тема деления чисел в данном отношении. Тема для учеников не всегда понятна с первого объяснения учителя, поэтому разберем ее подробнее на страницах сайта 7 гуру. Напишем понятия и правила, разберем примеры решения задач на деление в данном отношении.

Понятие отношения

Частное двух не равных нулю чисел a и b называется отношением чисел a и b. Числа a и b называются членами отношения.

Скорость – это отношение пройденного пути ко времени, за которое этот путь пройден.
Скорость сближения – это расстояние, на которое сближаются объекты за единицу времени.
Цена товара – это отношение стоимости товара к его массе или количеству единиц товара.

Правило деления числа в данном отношении.

Чтобы разделить число c в отношении a к b, можно разделить число c на сумму членов отношения a + b и результат умножить на каждый член отношения, числа a, b и c не равны нулю.

Задача 1. Разделите между двумя друзьями 80 конфет в отношении 1:4.

1 способ:
Таким способом мы решали подобные задачи в начальной школе. Сначала узнаем, сколько всего частей в целом. Узнаем количество предметов в одной части. Умножаем на нужные количества частей, чтобы ответить на вопрос.

2 способ:
Решаем по правилу деления числа на части. Этим способом предпочтительнее пользоваться при решении подобных задач.

Ответ: конфеты между друзьями надо разделить так: первому – 16 конфет, а второму – 64 конфеты.

Задача 2. Сестра и брат сложили свои деньги для покупки лотерейного билета. У сестры было 50 рублей, а у брата 30 рублей. Билет выиграл 4000 рублей. Как они должны разделить эти деньги между собой?

Ответ: 2500 рублей, 1500 рублей.

Задача 3. Трое хотят купить фирму по продаже мороженого. Первый желает иметь 6 частей акций, второй – 4 части акций, третий – 2 части. Всего нужно заплатить 960 000 рублей. Сколько денег должен внести каждый из них.

Ответ: 480 000 рублей, 320 000 рублей, 160 000 рублей.

Задача 4. Первая машинистка печатает 180 страниц за 20 часов, а вторая – за 30 часов. Как распределить между ними 180 страниц, чтобы они напечатали их в кратчайший срок?

Ответ: первой машинистке – 108 страниц, второй – 72 страницы.

Задача 5. Мотоциклист может проехать расстояние между пунктами за 4 часа, а велосипедист – за 12 часов. Однажды они одновременно отправились навстречу друг другу из этих пунктов. Сколько километров проедет каждый до встречи, если расстояние между пунктами 120 километров?

Так как время преодоления расстояния мотоциклистом и велосипедистом равно 12:4, значит, скорость мотоциклиста будет в 3 раза больше, чем велосипедиста. Следовательно, за одно и то же время мотоциклист проедет в 3 раза большее расстояние. Это значит, что весь путь делится между ними в отношении 1:3.

Задача 6. Сортировка элементов по категориям. Поставьте в соответствующие столбцы (1:4; 2:5) числа, которые можно разделить нацело в заданных отношениях. Варианты ответов: 25, 13, 14, 45, 28, 6.

Для решения нужно сначала посчитать сумму частей первого столбца:
1 + 4 = 5
Затем проверить, какие из чисел кратны 5. Это 25 и 45.
Аналогично для второго столбца.
2 + 5 = 7
Числа, кратные 7: 14 и 28.

Источник

Конспект урока по математике на тему » Деление числа в данном отношении. Основные понятия»

Тема урока: Деление числа в данном отношении. Основные понятия

Цель урока: Проверить знания учащихся по теме «Масштаб». Научится делить число в данном отношении; формирование навыков решения задач по теме.

Планируемые результаты: Предметные

Знать: правило деления числа в данном отношении. Уметь: применять правило при решении заданий.

Регулятивные: принимать учебную задачу; планировать (в сотрудничестве с учителем и одноклассниками или самостоятельно) необходимые действия, операции, действовать по плану; осуществлять самоконтроль и самооценку; осознание качества и уровня усвоения.

Познавательные: самостоятельно выделять и формулировать познавательную цель; умения работать с имеющейся информацией в новой ситуации ; осуществлять для решения учебных задач операции анализа, синтеза, сравнения; устанавливать причинно-следственные связи, делать выводы.

Коммуникативные: вступать в учебный диалог с учителем, одноклассниками, участвовать в общей беседе, соблюдая правила речевого поведения; формулировать собственное мнение;

задавать вопросы, слушать и отвечать на вопросы других, строить небольшие монологические высказывания ;

Личностные: р азвитие навыка самостоятельности в работе, трудолюбия, аккуратности, развитие навыков самоанализа и самоконтроля при оценке результата и процесса своей деятельности.

Оборудование: учебник «Математика, 6 класс» Никольский С.М., Шевкин А.В., оценочный лист, тетрадь, карточки – задания, презентация к уроку.

Тип урока: урок изучения нового материала

Приветствует учащихся, организует рабочее место.

Проверка учителем готовности класса к уроку; организация внимания; инструктаж по работе с листом самооценки.

Добрый день, добрый час!
Как я рада видеть вас.
Друг на друга посмотрели
И тихонько дружно сели.

Девизом нашего урока будут слова канадского математика Айвена Нивена: «Математику нельзя изучать, наблюдая как это делает сосед»

— Как вы понимаете эти слова?

Предлагает ответить на поставленные вопросы:

— Что ж, ребята выполним устный счет и повторим табличное умножение и деление.

— А теперь, ребята давайте с вами повторим понятие, с которым знакомились на предыдущих трех уроках. А это было понятие?

Верно, масштаб. А что называют масштабом?

( Масштаб – это отношение длины отрезка на плане к его настоящей длине.)

Самостоятельная работа по теме «Масштаб».

Теперь нам с вами необходимо проверить знания по теме «Масштаб»

Раздает карточки с заданиями в 2-х вариантах

Организует выполнение комплекса упражнений

Мы работали отлично,

Отдохнуть не прочь сейчас,

И зарядка к нам привычно

На урок приходит в класс.

Раз – подняться, потянуться

Два – нагнуться, разогнуться

Три – в ладоши, три хлопка

На четыре – руки шире

Пять – руками помахать

Шесть – на место тихо сесть

Целепологание и мотивация

Подготовить учащихся к изучению новой темы.

— Чтобы обозначить тему нашего урока посмотрите на это сочетание букв. Прочитайте его но без букв У и К:

какие цели поставим на этот урок?

Я согласна с вами. Цель урока: Познакомиться с правилом деления числа в данном отношении и научиться применять при решении заданий.

— Но нам необходимо сначала вспомнить, что же такое отношение? ( Частное двух не равных нулю чисел a и b называют отношением чисел a и b .)

Изучение нового материала

-Ребята, для того, чтобы познакомиться с новым правилом, решим вот такую задачу.

Пусть требуется разделить между двумя друзьями 60 конфет в отношении 2 : 3.

1 друг – ? конфет

— Умеем ли мы с вами решать такие задачи?

— А другим способом мы можем решить эту же задачу?

— Да ребята, мы с вами пока можем решать только одним способом, а теперь рассмотрим еще один.

1) 2 + 3 = 5 (частей) – составляют все конфеты;

2) 60 : 5 = 12 (конфет) – приходится на 1 часть;

3) 2 × 12 = 24 (конфеты) – приходится на 2 части, это для 1 друга;

4) 3 × 12 = 36 (конфет) – приходится на 3 части, это для 2 друга.

1) (конфеты) – приходится на 2 части, это для 1 друга;

2) (конфет) – приходится на 3 части, это для 2 друга.

Ответ : 24 конфеты, 36 конфет.

Выведем правило деление числа в данном отношении.

Таким образом, чтобы разделить число 60 в отношении 2 : 3, можно разделить число 60 на сумму членов отношения 2 + 3 и результат умножить на каждый член отношения.

Запишем определение в общие тетради.

1 число: ;

2 число: .

Первичное закрепление во внешней речи

-Предлагает прочитать в учебнике определения.

— Рассмотрим еще одну задачу и ее решение оформим в тетрадях:

Задача 1. Два брата сложили свои деньги для покупки акций. Старший внес 500 р., а младший – 300 р. Через некоторое время они продали акции за 1000 р. Как они должны разделить эти деньги между собой?

Естественно разделить 100 р. в том отношении в котором они вложили деньги, т.е. в отношении 500 : 300 = 5 : 3.

1) старшему брату ;

2) младшему брату .

Решим устно. После сбора урожая яблок одна их часть была высушена, а другая использована для приготовления сока. Сколько яблок пошло на сушку, а сколько на сок?

Источник