Что такое деление комплексных чисел

Правила деления комплексных чисел

Деление комплексных чисел — основные правила

Частным двух комплексных чисел \(z_<1>=a_<1>+b_ <1>i\) и \(z_<2>=a_<2>+b_ <2>\) i называют число z, заданное соотношением: \(z=\frac>>=\frac a_<2>+b_ <1>b_<2>>^<2>+b_<2>^<2>>+\frac b_<1>-a_ <1>b_<2>>^<2>+b_<2>^<2>> i\)

Общий алгоритм для деления комплексных чисел на практике:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

В каких формах это можно делать

Комплексные числа делят разными методами, подтвержденными доказательствами. Существуют алгебраическая, тригонометрическая и показательная формы для подобных операций. В каждом перечисленном случае необходимо использовать определенную формулу.

Формула деления в алгебраической форме

Когда требуется выполнить деление комплексных чисел в алгебраической форме, в первую очередь числитель и знаменатель умножают на число, сопряженное к знаменателю. Таким образом, удается исключить комплексность в знаменателе:

Формула деления в тригонометрической форме

Деление в тригонометрической форме подразумевает деление модулей комплексных чисел. После выполнения данной операции определяют разность аргументов:

Формула деления в показательной форме

Показательная форма деления комплексных чисел в тригонометрии предполагает деление модулей и вычисление разности аргументов в экспоненте:

Примеры решения задач

Необходимо найти частное пары комплексных чисел:

\(z_1 = 3+i\) и \(z_2 = 2-3i\)

Заметим, что комплексные числа заданы в алгебраической форме. В связи с этим целесообразно использовать в действиях соответствующую формулу.

Сопряженное комплексное число к знаменателю:

Нужно домножить и разделить на сопряженное комплексное число к знаменателю дроби. Таким образом, получится исключить комплексность в знаменателе:

Далее следует привести подобные слагаемые и записать вывод с ответом:

Требуется выполнить деление комплексных чисел:

Комплексные числа в условии задачи записаны в тригонометрической форме. По этой причине необходимо использовать в расчетах соответствующую формулу. В данном случае следует определить деление модулей и разность аргументов:

Следующим шагом является деление чисел:

Нужно найти частное комплексных чисел:

Решение: Согласно формуле деления в показательной форме определяем разность аргументов и частное модулей:

При подстановке в формулу полученных значений уравнение будет преобразовано следующим образом:

В первую очередь следует домножить числитель и знаменатель заданной дроби на число, комплексно сопряженное к знаменателю:

Данным числом является:

Затем следует перемножить комплексные числа, как алгебраические двучлены, с учетом:

Необходимо найти частное:

\(=2 \cdot\left[\cos \frac<\pi><2>+i \sin \frac<\pi><2>\right]=2 \cdot(0+i)=2 i\)

Необходимо разделить два комплексных числа:

С помощью соответствующей формулы можно записать уравнение:

Ответ: \( z_ <1>\div z_ <2>= 1+i\)

Необходимо вычислить частное комплексных чисел:

\(z_<1>=\sqrt <2>\left( \cos \frac<\pi> <2>+ i \sin \frac<\pi> <2>\right)\)

\(z_<2>=\sqrt <2>\left( \cos \frac<\pi> <4>+ i \sin \frac<\pi> <4>\right)\)

Используя соответствующую формулу, запишем:

\(z_ <1>\div z_ <2>= \frac>> (\cos ( \varphi _ <1>— \varphi _<2>) + i \sin ( \varphi _ <1>— \varphi _<2>)) = \frac<\sqrt<2>><\sqrt<2>> \left( \cos \left( \frac<\pi><2>-\frac<\pi> <4>\right) + i \sin \left( \frac<\pi><2>-\frac<\pi> <4>\right) \right) =\)

\(= 1 \cdot \left( \cos \frac<\pi> <4>+ i \sin \frac<\pi> <4>\right) = \cos \frac<\pi> <4>+ i \sin \frac<\pi><4>\)

Ответ: \( z_ <1>\div z_ <2>= \cos \frac<\pi> <4>+ i \sin \frac<\pi><4>\)

Требуется разделить два комплексных числа:

Используя соответствующую формулу деления комплексных чисел, можно решить уравнение:

Источник

Деление комплексных чисел

Вы будете перенаправлены на Автор24

Деление на число и деление заданных комплексных чисел выполняются для чисел, представленных в любой форме записи.

Для деления заданных комплексных чисел на действительное число воспользуемся определением и получим:

Готовые работы на аналогичную тему

\[z_ <1>\cdot z_ <2>=\frac > > \cdot [\cos (\varphi _ <1>-\varphi _ <2>)+i\sin (\varphi _ <1>-\varphi _ <2>)].\]

Выполнить деление заданных комплексных чисел:

Для деления заданных комплексных чисел воспользуемся определением и получим:

Равенство, указанное в определении 3, достаточно сложно для запоминания, поэтому на практике при делении заданных комплексных чисел, представленных в алгебраической форме, используют алгоритм, который описан в примечании 5.

Чтобы выполнить операцию деления заданных комплексных чисел, представленных в алгебраической форме необходимо:

Выполнить деление комплексных чисел:

Для деления комплексных чисел воспользуемся алгоритмом, приведенным в примечании 5, и получим:

Выполнить деление комплексных чисел:

Для деления комплексных чисел воспользуемся определением и получим:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 13 11 2021

Источник

Комплексные числа — простое объяснение. Сложение, вычитание, умножение и деление комплексных чисел

Комплексные числа не так сложны, как могло бы показаться. В начале они назывались невозможными числами. Также их еще называли мнимыми или воображаемыми, поскольку действительно чтобы их представить, требуется немного воображения. В данном обзоре постараемся в доступной форме с наглядными примерами разобраться с данными числами.

Комплексные числа — простое объяснение

Для того, чтобы разобраться с комплексными числами, следует для начала рассмотреть множество действительных чисел. К этому множеству относятся целые числа, и дроби, и иррациональные числа. При этом каждой точке числовой прямой обязательно соответствует некоторое действительное число.

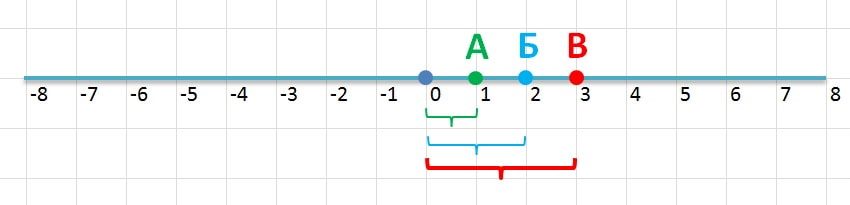
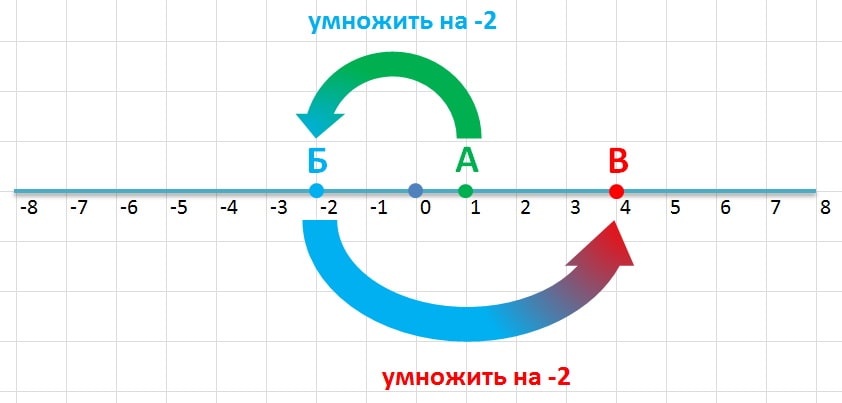
Рассмотрим две точки на прямой А = 1 и Б = 2. Сложим эти две точки. Их сумма эта третья точка В = 1+2 = 3.

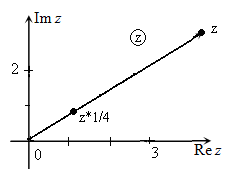
Точки также можно перемножать. Посмотрим, например, как действует умножения на минус 2. Данное действие преобразует точку 1 в минус 2. Если мы снова умножим на минус 2, то нужно будет повторить аналогичное передвижение на прямой, поменять стороны относительно начала координат и удвоить расстояние до него. В результате получим 4.

Умножение на минус 1 устроено просто. Каждая точка переходит в симметричную ей относительно начала координат. Другими словами нужно сделать пол оборота (повернуть на 180°). Повторение умножения на минус 1 приводит в исходное положение. Умножение на минус 1 переводит 1 в минус 1. Если еще раз умножить на минус 1, мы вернемся обратно в 1.

На данном этапе можно выделить правило, что если умножить число на себя, результат всегда будет положительным. Другими словами минус 1 не имеет квадратного корня. Но только не в случае с комплексными числами.

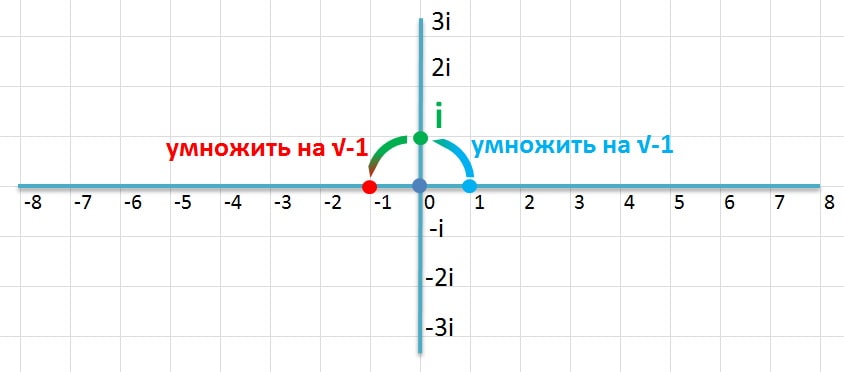
В начале 19 века Робер Арган высказал следующую идею. Поскольку умножить на минус 1 означает повернуть на 180°, то квадратный корень из минус 1 означает повернуть на половину (90°). Если повернуть дважды на четверть оборота, вы сделаете пол оборота. Квадрат четверти оборота — это пол оборота (минус 1). То есть квадратный корень из минус 1 отвечает точке, в которую минус 1 переходит при повороте на 90°. Поскольку такое построение, выходящее за пределы горизонтальной прямой, выглядит странным, говорят, что такая точка, являющаяся квадратным корнем из минус 1 — это мнимое число. И в математике оно обозначается — i.

С выходом за пределы прямой, все последующие действия производятся легко. Можно отметить числа 2i, 3i и так далее. Каждой точке плоскости отвечает комплексное число. И наоборот — всякое комплексное число задает точку на плоскости.

Операции с комплексными числами

Так же как и для вещественных чисел, для комплексных чисел определены операции сложения, вычитания, умножения и деления. Однако многие свойства комплексных чисел отличаются от свойств вещественных чисел. Например, нельзя указать, какое из двух комплексных чисел больше или меньше.

Сложение и вычитание комплексных чисел

Комплексные числа могут складываться и вычитаться как обычные.

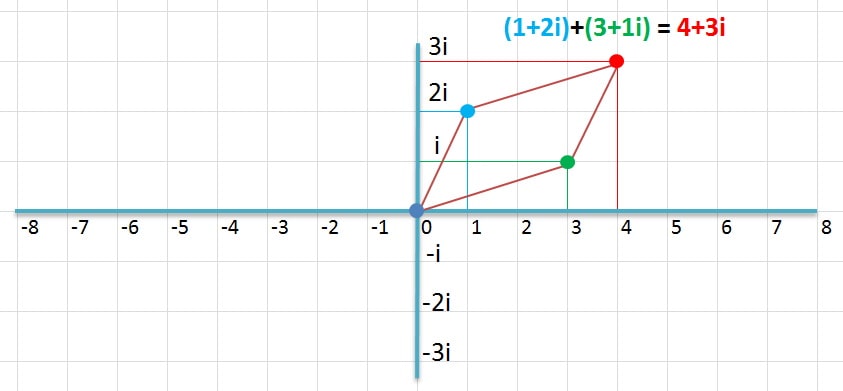
Рассмотрим точку, обозначающую число 1+2i. Прибавим к нему число 3+1i. Можно сложить столбиком и получить 4+3i. Геометрически это обычное сложение векторов.

Разность комплексных чисел, записанных в алгебраической форме, представляет собой комплексное число, действительная часть которого и коэффициент при мнимой части равны соответственно разности действительных частей и разности коэффициентов при мнимой части уменьшаемого и вычитаемого.

В общем виде вычитание комплексных чисел z1 = a+bi и z2 = c+di можно записать так: z1-z2 = (a+bi)-(c+di) = (a-c)+(b-d)i.

Несколько примеров вычитания:

Умножение и деление комплексных чисел

Комплексные числа перемежаются точно также, как и действительные числа. Рассмотрим несколько примеров.

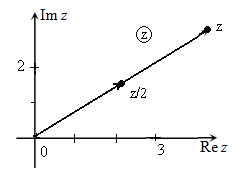
2×(1+1i) = 2+2i. Геометрически умножение на два выглядит как растягивание прямой с точкой на плоскости в два раза.

Частное комплексных чисел z1 = x1+y1i и z2 = x2+y2i в алгебраической форме находится путем домножения числителя и знаменателя на сопряженное число к знаменателю:

z1÷z2 = (x1+y1i)÷(x2+y2i) = ((x1+y1i)×(x2-y2i))÷((x2+y2i)×(x2-y2i)) = ((x1×x2+y1×y2)÷(x2²+y2²)) + (i×(x2×y1-x1×y2)÷(x2²+y2²)).

Комплексные числа — тригонометрическая форма

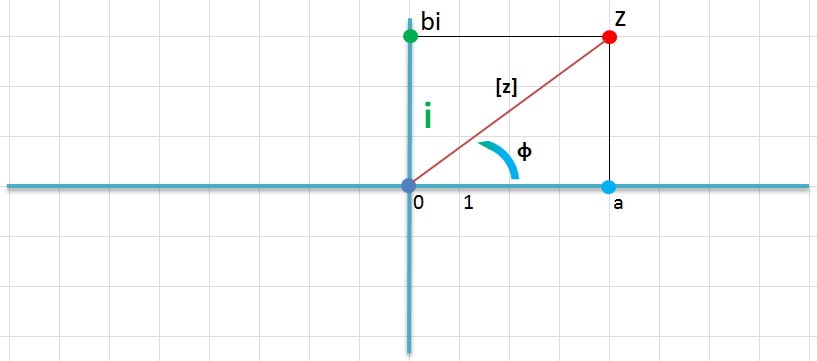
Казалось бы, плоскость двухмерная, так как для описания произвольной точки нужны два числа. На самом же деле можно обойтись одним числом. Для этого используется тригонометрическая форма представления. То есть z = a+bi можно представить как z = [z]×(cosφ+i×sinφ), где:

По теореме Пифагора легко вывести формулу для нахождения модуля комплексного числа: [z] = √(a²+b²). Данная формула справедлива для любых значений a и b.

Для нахождения аргумента (φ или argz) нужно воспользоваться следующими формулами:

Как видно, комплексные числа не так сложны, как могло бы показаться на первый взгляд. Ознакомившись с простым объяснением и методикой работы с ними, вы научитесь складывать, вычитать, умножать и делить комплексные числа. Также вы сможете переводить комплексные числа из алгебраической формы в тригонометрическую.

Источник

Деление комплексных чисел

Определим деление следующим образом:

Деление комплексных чисел находящихся в алгебраической форме происходит по понятной схеме. Однако непонятно, какой геометрический смысл деления.

Пусть комплексные числа и заданы в тригонометрической форме:

Эта формула получается из правила умножения комплексных чисел: При умножении одного комплексного числа на другое, модули этих чисел перемножаются, а аргументы складываются. Приведенная формула деления одного комплексного числа на другое означает, что модули чисел делятся, а аргументы вычитаются.

Длины волн инфракрасного света достаточно велики, чтобы перемещаться сквозь облака, которые в противном случае блокировали бы наш обзор. Используя большие инфракра сные телескопы, астрономы смогли заглянуть в ядро нашей галактики. Большое количество звезд излучают часть своей электромагнитной энергии в виде видимого света, крошечной части спектра, к которой чувствительны наши глаза.

Так как длина волны коррелирует с энергией, цвет звезды говорит нам, насколько она горячая. Используя телескопы, чувствительные к различным диапазонам длин волн спектра, астрономы получают представление о широком круге объектов и явлений во вселенной.

Пример №1 Постройте центральную симметрию тетраэдра, относительно точки O, изображенных на рисунке 3.

Для построения такой центральной симметрии сначала проведем через все точки тетраэдра прямые, каждая из которых будет проходить через точку O. На них построим отрезки, удовлетворяющие условиям |AO|=|A?O|, |BO|=|B?O|, |CO|=|C?O|, |DO|=|D?O| Таким образом, и получим искомую симметрию (рис. 4).

В ряду разных механических движений особенным значением обладают колебания. Это движения и процессы, имеющие периодичность во времени.

В среде электромагнитных явлений также значительное место заняли электромагнитные колебания. В этих колебаниях заряды, токи, электрические и магнитные поля изменяются согласно периодическим законам.

Совет №1 Велосипедист, имеющий скорость 300 м/с, или идеальный газ, оказывающий давление 100 паскалей в большой тепловой машине — это странно.

Нужна помощь с курсовой или дипломной работой?

Источник

Алгебраические операции с комплексными числами

Содержание:

Действия над комплексными числами, заданными в алгебраической форме

Алгебраическая форма комплексного числа

Как отмечалось ранее, комплексное число можно задавать в виде или . Последующее изучение комплексных чисел показывает, что комплексные числа можно задавать и другими способами.

Комплексное число, заданное в виде , называется комплексным числом в алгебраической форме.

Рассмотрим действия над комплексными числами, заданными в алгебраической форме.

Сложение комплексных чисел

Следовательно, чтобы сложить два комплексных числа, нужно сложить их действительные части, что дает действительную часть суммы, и сложить мнимые части, что дает мнимую часть суммы.

Сумма комплексно-сопряжённых чисел всегда является действительным числом.

Следовательно,

Свойства суммы комплексных чисел

1. Сложение комплексных чисел является коммутативным, то есть для любых комплексных чисел справедливо равенство

2. Сложение комплексных чисел является ассоциативным, то есть для любых комплексных чисел справедливо равенство

Возможно вам будут полезны данные страницы:

Вычитание комплексных чисел

Определение. Разностью двух комплексных чисел называется такое число, которое в сумме с вычитаемым дает уменьшаемое.

Вычитание комплексных чисел является всегда возможным.

Теорема Для любых комплексных чисел всегда существует разность , определяемая однозначно.

Докажем, что существует такое число , которое удовлетворяет условию , то есть что или . На основании равенства комплексных чисел приходим к системе уравнений

Эта система уравнений имеет решение, и к тому же лишь одно, а именно:

что и нужно было доказать.

Разность комплексно-сопряжённых чисел всегда является мнимым числом.

Умножение комплексных чисел

Определение. Произведением двух комплексных чисел и называется комплексное число, определяемое формулой

Произведение комплексно-сопряжённых чисел всегда является действительным числом.

Свойства произведения комплексных чисел

1. Умножение комплексных чисел является коммутативным, то есть для любых комплексных чисел справедливо равенство

2. Умножение комплексных чисел является ассоциативным, то есть для любых комплексных чисел справедливо равенство

3. Умножение комплексных чисел является дистрибутивным относительно сложения, то есть для любых комплексных чисел справедливо равенство

Деление комплексных чисел

Определение. Частным от деления комплексных чисел называется такое комплексное число, которое в произведении с делителем дает делимое, если делитель отличается от нуля.

Докажем, что всегда существует частное от деления двух комплексных чисел, если знаменатель отличается от нуля.

Теорема Частное определяется однозначно для любых комплексных чисел если

Пусть . Докажем, что существуют такие числа х и у, которые удовлетворяют уравнению Выполнив умножение, получим:

Исходя из равенства комплексных чисел, имеем систему уравнений

Решив эту систему уравнений, находим

Следовательно, система уравнений имеет решение, и к тому же единственное. Тогда

ЗАМЕЧАНИЕ. Деление комплексных чисел в алгебраической форме удобно выполнять следующим образом. Числитель и знаменатель следует умножить на число, комплексно-сопряженное знаменателю, после чего в числителе и знаменателе выполнить умножение комплексных чисел по правилу умножения многочленов. Полученный результат записать в алгебраической форме.

Примеры с решением

Пример задачи с решением 2.1

Решение:

Использовав формулы (2.1), (2.2), (2.5), (2.6), получим:

Ответ:

Пример задачи с решением 2.2

Найти значение выражения

Решение:

Воспользовавшись правилом умножения многочленов, имеем

Ответ:

Пример задачи с решением 2.3

Решение:

Воспользуемся правилом умножения многочленов:

4) По формуле (2.8) имеем:

Ответ:

Пример задачи с решением 2.4

Решение:

Деление комплексных чисел можно выполнять по формуле (2.13), но проще это сделать, умножив числитель и знаменатель на число, комплексносопряжённое знаменателю.

Ответ:

На странице -> решение задач по электротехнике собраны решения задач и заданий с решёнными примерами по всем темам теоретических основ электротехники (ТОЭ).

Услуги:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник