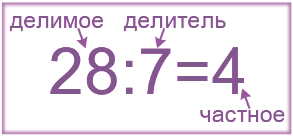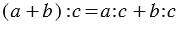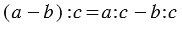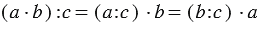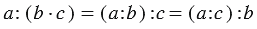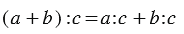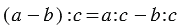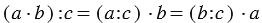Что такое делитель и делимое в математике

Деление целых чисел. Делимое, делитель, частное.

Деление целых чисел отличается от деления натуральных чисел, только тем что у целых чисел нужно у частного посчитать знак. Как посчитать знак частного целых чисел? Рассмотрим подробно в теме.

Термины и понятия частного целых чисел.

Чтобы выполнить деление целых чисел нужно вспомнить термины и понятия. В делении есть: делимое, делитель и частное целых чисел.

Делимое – это то целое число, которое делят. Делитель – это целое число, на которое делят. Частное – это результат деления целых чисел.

Можно сказать “Деление целых чисел” или “Частное целых чисел” смысл этих фраз один и тот же, то есть нужно поделить одно целое число на другое и получить ответ.

Деление берет свое начало из умножения. Рассмотрим пример:

У нас есть два множителя 3 и 4. Но допустим нам известно, что есть один множитель 3 и результат умножения множителей их произведение 12. Как найти второй множитель? На помощь приходит деление.

Правило деления целых чисел.

Частное двух целых чисел равно частному их модулей, со знаком плюс в результате, если числа одинаковых знаков, и со знаком минус, если они разных знаков.

Важно учитывать знак частного целых чисел. Кратко правила деления целых чисел:

Плюс на плюс дает плюс.
“+ : + = +”

Минус на минус дает плюс.
“– : – =+”

Минус на плюс дает минус.
“– : + = –”

Плюс на минус дает минус.
“+ : – = –”

А теперь рассмотрим подробно каждый пункт правила деления целых чисел.

Деление целых положительных чисел.

Вспомним, что целые положительные числа это тоже самое, что натуральные числа. Мы пользуемся теми же правила, что и при делении натуральных чисел. Знак частного от деления целых положительных чисел всегда плюс. Иными словами, при делении двух целых чисел “плюс на плюс дает плюс”.

Пример:
Выполните деление 306 на 3.

Решение:
Оба числа имеют знак “+”, поэтому ответ будет со знаком “+”.
306:3=102
Ответ: 102.

Пример:
Разделите делимое 220286 на делитель 589.

Решение:
Делимое 220286 и делитель 589 имеет знак плюс, поэтому частное тоже будет иметь знак плюс.
220286:589=374
Ответ: 374

Деление целых отрицательных чисел.

Правило деления двух отрицательных чисел.

Пусть у нас будут два отрицательных целых числа a и b. Нам нужно найти их модули и выполнить деление.

Результат деления или частное двух отрицательных целых чисел будет со знаком “+” или “минус на минус дает плюс”.

Решение:
-504:(-14)=|-504|:|-14|=504:14=34
Записать выражение можно короче:
-504:(-14)=34

Деление целых чисел с разными знаками. Правило и примеры.

При выполнении деления целых чисел с разными знаками, частное будет равно отрицательному числу.

Не важно положительное целое число делим на отрицательное целое число или отрицательное целое число делим на положительное целое число, результат деления всегда будет равен отрицательному числу.

Минус на плюс дает минус.
Плюс на минус дает минус.

Пример:
Вычислите деление 4716:(-524).

Нуль деленный на целое число. Правило.

При деление нуля на целое число ответ будет равен нулю.

Пример:
Выполните деление 0:558.

На нуль делить нельзя.

Нельзя 0 разделить на 0.

Проверка частного деления целых чисел.

Как говорилось ранее деление и умножение тесно связаны. Поэтому чтобы проверить результат деления двух целых чисел, нужно выполнить умножение делителя и частного в результате должно получиться делимое.

Проверка результата деления краткая формула:
Делитель ∙ Частное = Делимое

Рассмотрим пример:
Выполните деление и сделайте проверку 1888:(-32).

Решение:
Обращаем внимание на знаки целых чисел. Число 1888 положительное и имеет знак “+”. Число (-32) отрицательное и имеет знак “–”. Поэтому при делении двух целых чисел с разными знаками ответ будет отрицательное число.
1888:(-32)=-59

А теперь выполним проверку найденного ответа:
1888 – делимое,
-32 – делитель,
-59 – частное,

Делитель умножаем на частное.
-32∙(-59)=1888

Вопросы по теме:
Что такое частное чисел?
Ответ: частное чисел – это результат деления деления двух чисел.

Как найти частное?
Ответ: нужно одно число поделить на другое, то есть делимое поделить на делитель и получим частное.

Чему равно частное от деления целых чисел?
Ответ: если целые числа делятся без остатка, то их частное равно целому числу. Иначе будет дробное число.

Что такое делимое и делитель?
Ответ: число которое делят называют делимым, а число на которое делят называют делителем.

Пример:
Найдите частное суммы и разности чисел 48 и 16.

Решение:
Находим сумму чисел 48 и 16.
48+16=64
Находим разность чисел 48 и 16.
48-16=32
Находим частное.
64:32=2
Ответ: 2.

Источник

Деление чисел

Деление — это арифметическое действие, с помощью которого можно узнать, сколько раз одно число содержится в другом.

Деление можно представить, как неоднократно повторяемое вычитание. Например, число 6 разделить на 2 — значит узнать, сколько раз число 2 содержится в 6:

Повторив вычитание 2 из 6, мы узнали, что 2 содержится в 6 три раза. Это можно проверить сложив три раза по 2 или умножив 2 на 3:

Для записи деления используется знак : (двоеточие), который ставится между числами. Например:

Эта запись означает, что 6 надо разделить на 2. Справа от записи деления ставится знак = (равно), после которого записывается полученный результат:

Задача. В магазин привезли 9 морковок. Продавщица связала их в пучки по 3 морковки в каждом пучке. Сколько получилось пучков?

Решение: Чтобы решить эту задачу, надо узнать, сколько раз по 3 содержится в числе 9. Для этого разделим 9 на 3. Получим 3.

Решение можно записать так:

Пример. Решить примеры на деление с помощью схем.

2) 12 : 4 = 3, 12: 3 = 4.

Делимое, делитель и частное

Делимое — это число, которое делят. Делитель — это число, на которое делят. Например, в записи:

12 — это делимое, 3 — делитель. Делитель показывает на сколько равных частей нужно разделить делимое.

Частное — это число, которое получается в результате деления. Например, в записи:

4 — это частное. При этом сама запись 12 : 3 тоже называется частным.

Проверка деления

где 28 — это делимое, 4 — это делитель, а 7 — частное. Чтобы узнать правильно ли было выполнено деление, можно:

или умножить делитель на частное:

Источник

Общее представление о делении натуральных чисел

В рамках этого материала мы разберем важное действие, называемое делением. Дав общее представление о нем и объяснив его смысл, мы введем основные термины и обозначения на письме. В последнем пункте мы расскажем, для решения каких задач нам пригодится умение делить натуральные числа.

Что такое деление натуральных чисел

Само по себе понятие деление неразрывно связано с процессом разъединения некоторого множества предметов на несколько отдельных множеств.

Объясним на примере.

В быту мы часто употребляем слова»делиться», «поделиться», например, поделиться угощением с друзьями. Это слово означает, что угощение мы поделили на некоторые части и отдали часть одним людям, а часть другим (или оставили себе). С помощью этого простого примера деление можно представить как последовательное вычитание из одного большого множества. Что такое вычитание и как его выполнять, мы уже разбирали с вами ранее.

Основной смысл процесса деления

На основе того, что мы озвучили, можно придать определенный смысл делению одного натурального числа на другое (отдельно выделим число, которое делят, и то, на которое делят). Мы помним, что понятие натуральных чисел проще всего соотнести с количеством некоторых предметов. То число, которое необходимо поделить, выражает число предметов исходного множества. В зависимости от того, какой смысл мы придаем второму числу (т.е. тому, на которое делят), можно выделить два основных подхода к пониманию смысла деления. Возможны такие варианты:

Разделить одно натуральное число на другое без остатка возможно далеко не всегда. Так, 10 конфет мы можем ровно разделить на 2 или 5 кучек, а на 3 нет, потому что в одном из множеств окажется отличное от других число конфет. Разложить 10 конфет по 15 или 20 кучкам мы также не в состоянии. Смысл таких действий объясняется в материале про деление с остатком.

Если мы можем поделить одно натуральное число на другое, то получившееся в итоге число также будет натуральным.

Основные понятия процесса деления

В этом пункте мы укажем основные обозначения и понятия, используемые в делении натуральных чисел.

Чтобы обозначить деление в записи, обычно используют знак двоеточия: « : ». Иногда можно встретить вместо него знак « ÷ », который означает то же самое. Первым мы записываем число, которое будем делить, потом знак деления, а потом число, на которое делим. Числовое выражение вида 10 : 5 означает, что мы делим десять на пять.

То число, которое делим, называем делимым. То, на которое делим – делителем. Итог вычислений правильно называть частным. Само числовое выражение, состоящее из делимого, делителя и знака деления, тоже называется частным.

Когда мы говорим о том, что нужно определить число, являющееся результатом деления одного натурального числа на другое, нужно использовать выражения «найти частное» или «вычислить частное».

Запись читается как «тридцать разделить на шесть равно пяти» или «частное от деления тридцати на шесть равно пяти».

Схематично процесс деления можно отобразить как » делимое : делитель = частное.».

Задачи с применением деления

Приведем примеры задач, для которых нужно уметь делить одно натуральное число на другое.

1. Первый тип задач – это те, в которых нужно найти, сколько множеств получится после деления исходного множества на равные части, а также близкие к ним задачи на вычисление количества предметов в каждом множестве после деления. Ранее мы уже приводили примеры таких задач. Добавим еще несколько.

Допустим, у нас есть 40 ручек, которые нужно распределить поровну между 4 коробками. Как вычислить, сколько ручек положить в каждую из них?

Ответ: 10

На ужин было приготовлено 12 котлет. Каждому члену семьи должно достаться по две. Сколько всего человек будут ужинать?

2. Второй тип задач очень схож с первым, однако в них необходимо вычислить не количество предметов, а изменения физических величин (времени, температуры, длины и др.)

Например, у нас есть полная бочка молока объемом 100 л. Сколько надо взять двухлитровых бутылок, чтобы перелить туда все имеющееся молоко?

Ответ: 100

Ответ: 3

3. Третий тип задач – это те, где нужно найти, во сколько раз уменьшилось исходное количество чего-либо, или выяснить, во сколько одно множество предметов или величина больше, чем другое. Например:

Планировалось построить дом площадью 120 кв м., но в итоге построили в два раза меньше. Какую площадь имеет в итоге построенный дом?

Ответ: 60

Источник

Математика. 2 класс

Конспект урока

Математика, 2 класс

Урок № 55. Название чисел при делении

Перечень вопросов, рассматриваемых в теме:

1. Как называются числа при делении?

2. Как называется числовое выражение со знаком деление?

Обязательная литература и дополнительная литература:

Теоретический материал для самостоятельного изучения

Запишем равенство, используя необходимое арифметическое действие:

10 яблок разложили на две тарелки поровну.

9 конфет раздали трём детям поровну.

8 тетрадей раздали четырём ученикам поровну.

Для того, чтобы выполнит задание, нам понадобилось действие деление.

Вы уже знаете, как называются числа при сложении и вычитании, недавно вы познакомились с названиями чисел при умножении.

Вы умеете называть выражения со знаками «плюс», «минус», со знаком умножения. Сегодня вы узнаете, как называются числа при делении. Выражение со знаком деления тоже имеет своё название. Хотите узнать? Вперёд!

Числа при делении имеют свои названия.

8 листьев раздали детям, по 2 листа каждому.

4 человека получили листья.

Число, которое делят, называется делимым. 8 – это делимое. Число, на которое делят делимое, называется делитель. 2 – это делитель Результат действия деления называется частным. 4 – это частное. Выражение 8 разделить на 2 тоже называется частным.

Компоненты деления: делимое, делитель, частное.

Найдите частное, если делимое – 6, делитель – 3.

Найдите частное чисел 12 и 6. Проверьте: 12 : 6 = 2

Решим задачу: 12 клубничек раздали 4 детям поровну. По сколько клубничек получил каждый ребёнок?

Для решения задачи выберем действие деление, так как надо узнать, сколько раз по 4 содержится в числе 12.

Ответ: по 3 клубнички получил каждый ребёнок.

Вспомним название чисел при делении. 12 – делимое, 4 – делитель. 3 – частное. 12 : 4 – это частное.

Вывод: компоненты действия деление – делимое, делитель, результат деления – частное.

Ответим на вопросы, поставленные в начале урока.

Число, которое делят, называется делимое.

Число, на которое делят делимое, называется делитель.

Результат деления – частное.

Числа, которые соединены знаком деления, тоже называются частное.

Выполним несколько тренировочных заданий.

1. По рисунку составьте задачи на деление. Запишите решение. Назовите компоненты действия деление.

а) 15 яблок разложили в 3 вазы, в каждую вазу поровну. Сколько яблок положили в одну вазу?

Проверьте: 15 : 3 = 5 (яб.).

15 – делимое. 3 – делитель. 5 – частное. Выражение 15:3 – частное.

б) 15 яблок разложили в вазы, по 5 штук в каждую. Сколько ваз заняты яблоками?

15 – делимое. 5 – делитель. 3 – частное. Выражение 15:5 – частное.

2. Запишите выражение и найдите их значения:

Источник

Деление натуральных чисел

Вы уже знакомы с общими понятиями о делении и о том как делить в столбик, рассмотрим более подробно деление натуральных чисел и его свойства.

Рассмотрим задачу:

У Вани 7 кроликов, он собрал для них 28 яблок. Сколько яблок досталось каждому кролику?

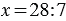
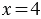
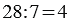
Данное действие записывают так: , или , где:

Частное показывает во сколько раз делимое больше делителя, то есть в нашем примере: 28 больше 7 в 4 раза. Поэтому, если в задаче звучит вопрос «во сколько?», для её решения мы используем деление. При этом не всегда возможно одно число поделить на другое, тогда возникает необходимость деления с остатком.

Из вышесказанного мы можем сделать вывод:

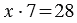
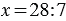
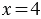
Пример: , следовательно, , то есть .

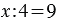
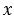
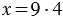
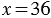
Пример: , по смыслу деления — это произведение 4 и 9, следовательно, , то есть .

Свойства деления

Распределительные свойства:

1. Деление суммы на число:

2. Деление разности на число:

3. Деление произведения на число:

4. Деление числа на произведение:

Действия с единицей и нулем

1. Деление числа на единицу: 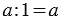то есть, при делении числа на единицу получается само число

2. Деление числа на себя: 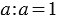, то есть при делении числа, не равного нулю, на само себя получается единица.

3. Деление нуля на число: 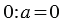, то есть при делении нуля на любое число, не равное нулю, получаем ноль.

НА НОЛЬ ДЕЛИТЬ НЕЛЬЗЯ!

Свойства деления

Распределительные свойства :

1. Деление суммы на число:

а) Мы можем сложить яблоки, которые нашли Маша и Ваня, а потом разделить полученное число на количество кроликов, то есть:

б) Мы можем разделить яблоки, которые собрала Маша, затем разделить яблоки, которые собрал Ваня, а результат сложить:

Мы видим, что в обоих случаях получается один и тот же результат, и можно записать, что: (9+15):3=9:3+15:3.

Вывод: Чтобы разделить сумму на какое-нибудь число, можно разделить на это число каждое слагаемое отдельно (если это возможно) и полученные частные сложить.

2. Деление разности на число:

Всего трем братьям папа дал 150 рублей. На 72 рубля они купили сестре цветы на день рождения. Сколько рублей осталось у каждого брата?

а) Мы можем из общей суммы вычесть то, что братья потратили, а затем поделить сдачу:

б) Мы можем найти, сколько получил каждый брат, затем посчитать, сколько потрачено каждым из них, а затем вычесть из полученной суммы денег потраченную:

Вывод: Чтобы разделить разность на какое-нибудь число, можно разделить на это число уменьшаемое и вычитаемое отдельно (если это возможно) и из первого частного вычесть второе.

3. Деление произведения на число:

В зооуголке в саду 3 кролика. 12 детей принесли по 6 яблок для кормления питомцев. Сколько яблок досталось каждому кролику?

а) Сначала можем найти общее количество яблок, которые принесли дети, а затем поделить на число кроликов:

б) Мы можем найти сколько детей принесли яблоки одному кролику, а затем умножить на количество принесенных яблок:

б) Мы можем найти по сколько яблок принес 1 ребенок для 1 кролика, а затем умножить на количество детей:

Мы видим, что в всех случаях получается один и тот же результат, и можно записать, что: (12 · 6) : 3 = (12 : 3) · 6 = (6 : 3) ·12.

Вывод: Чтобы разделить произведение двух множителей на число, можно разделить на это число любой из множителей (если деление выполнимо) и частное умножить на второй множитель.

4. Деление числа на произведение:

В 4 клетках сидят по 3 кролика. Ваня принес 48 яблок. Сколько яблок досталось каждому кролику?

а) Мы можем найти сколько кроликов всего, а потом поделить яблоки на полученное число:

б) Мы можем найти сколько яблок положат в каждую клетку, а затем, сколько получит яблок каждый кролик:

Если мы рассадим наших кроликов по 4 в три клетки, решая задачу аналогично получим:

Мы видим, что в всех случаях получается один и тот же результат, и можно записать, что: 48 : (4 · 3) = (48 : 4) : 3 = (48 : 3) : 4

Вывод: Чтобы разделить число на произведение двух множителей, можно разделить это число сначала на один из множителей, а затем на второй.

Действия с единицей и нулем

1. Деление числа на единицу:

У Вани один кролик. Он принёс 3 яблока. Сколько яблок достанется кролику?

Будем рассуждать, у Вани всего один кролик, значит все яблоки достанутся ему:

2. Деление числа на себя:

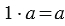
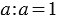
Из свойств умножения мы знаем, что: , а мы знаем, что по смыслу деления можно записать, что: , то есть при делении числа, не равного нулю, на само себя получается единица.

3. Деление нуля на число:

Рассуждая аналогично пункту 2 получаем: 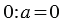, то есть при делении ноля на любое число, не равное нулю, получаем ноль.

Обратите внимание, что НА НОЛЬ ДЕЛИТЬ НЕЛЬЗЯ!

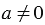
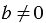
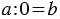
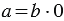
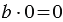
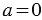
Это легко объяснить следующими рассуждениями: пусть мы взяли карандашей, попробуем разложить их в 0 коробок, и предположим, что получилось по карандашей в каждой коробке: , из смысла деления , в то же время мы знаем из свойств умножения, что: , то есть получаем, что , а это противоречит условию задачи, следовательно делаем вывод, что на ноль делить нельзя.

Поделись с друзьями в социальных сетях:

Источник