Что такое дельта в сопромате

ПроСопромат.ру

Технический портал, посвященный Сопромату и истории его создания

Обозначения

Какие обозначения приняты в сопромате?

А – площадь поперечного сечения брутто, м 2 ;

а – размер стороны прямоугольника, м;

а – расстояние между параллельными осями, м;

а – длина силового участка, м;

а – ордината эпюры изгибающих моментов, Нм;

b – расстояние между параллельными осями, м;

b – ширина сечения, м;

b – ордината эпюры изгибающих моментов, Нм;

С – центр тяжести сечения;

с – размер сечения или его части, м;

с – длина силового участка, м;

с – ордината эпюры изгибающих моментов, Нм;

D – диаметр наружный сечения, м;

d– ордината эпюр изгибающих моментов, м;

d– диаметр внутренний сечения, м;

Е – модуль упругости I рода, модуль Юнга, Па;

F – сила, Н;

— 1 единичная сила, н;

G – модуль сдвига, Па;

g – ускорение свободного падения (м/с 2 );

Н – высота падения ударяющего тела, м;

I_x, I_y – осевые моменты инерции сечения, м 4 ;

I_ρ – полярный момент инерции сечения, м 4 ;

I_max, I_min – главные центральные моменты инерции сечения, м 4 ;

i – индекс у сил и усилий;

k_σ, k_τ– эффективные коэффициенты концентрации напряжений, безразмерные;

ℓ — длина стержня или силового участка, м;

М – сосредоточенный момент, Нм;

М_х, М_у – изгибающие моменты (внутренние), Нм;

М_к – крутящий момент (внутренний, может обозначаться Т (фр.)).

М_к, М_н – значения внутренних изгибающих моментов в конце и начале силового участка, Нм;

— единичная пара сил,

N – нормальная или продольная сила (внутренняя), н;

n – коэффициент запаса прочности (может быть обозначен как k);

[n] или n_adm – допускаемый коэффициент запаса прочности;

[n_уст ] или n_{уст adm}– допускаемый коэффициент запаса на устойчивость;

n_в – скорость вращения вала, об/мин;

Р – полное напряжение, Па;

Q (Q_x, Q_y) – поперечная сила (внутренняя), н;

q – погонная нагрузка, н/м;

q_σ,q_τ – коэффициенты чувствительности к концентрации напряжений, безразмерная;

R – равнодействующая сил, н;

S_x, S_y – статические моменты площади сечения, м 3 ;

t_i – усилие в ветви ремня (ременной передачи), н;

u – удельная потенциальная энергия деформирования;

u_р – удельная потенциальная энергия изменения формы;

u_max, u_min – главные центральные оси;

u – перемещение в направлении оси Х, м;

v – перемещение в направлении оси у, м;

v – скорость ударяющего тела. м/с 2 ;

w – перемещение в направлении оси z, м;

W_i – мощность, передаваемая шестерней, колесом и т.п., кВт;

W_x, W_y – осевые моменты сопротивления, м 3;

W_ρ – полярный момент сопротивления, м 3 ;

W_к – момент сопротивления при кручении, м 3 ;

х – горизонтальная ось сечения;

у – вертикальная ось сечения;

х₀, у₀ – центральные оси сечения;

y_max – координата точки, наиболее удаленной от нейтральной линии;

[σ] или σ_adm – допускаемое напряжение, Па;

σ_к – критическое напряжение, Па;

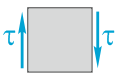
τ (τ_ху, τ_уz, τ_zx) – касательное напряжение, Па;

φ – угол поворота сечения при кручении, град;

φ – коэффициент понижения допускаемого напряжения, безразмерный;

α – угол, определяющий положение осей, град;

α₀ – угол, определяющий положение главных центральных осей, град;

β_σ β_τ – коэффициент, учитывающий влияние качества поверхности на усталость, безразмерная;

γ – удельный вес, н/м 3 ;

∆ – перемещение (линейное, м; угловое, рад);

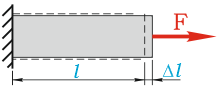
∆ℓ – абсолютная линейная деформация (удлинение или укорочение), м;

∆b – абсолютная поперечная деформация, м;

∆S – абсолютный сдвиг, м;

ε – относительная линейная деформация, безразмерная;

ε_пр, ε_поп – относительные продольная и поперечная деформации, безразмерные;

ε_σ ε_τ – коэффициенты, учитывающие влияние размеров деталей на предел выносливости, безразмерные;

θ – относительный (погонный) угол поворота, рад/м;

λ – гибкость стержня, безразмерная;

μ – коэффициент Пуассона, безразмерная;

ν – коэффициент приведения длины, безразмерная;

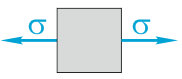
σ (σ_х, σ_у, σ_z) – нормальное напряжение, Па;

σ₁, σ₂, σ₃ – главные напряжения, Па;

σ_пр или σ_pr– предел пропорциональности, Па;

σ_т илиσ_у – предел текучести, Па;

σ_пр или σ_u– предел прочности, Па.

Источник

iSopromat.ru

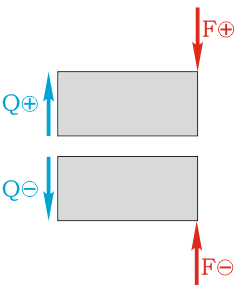
Правило знаков поперечных сил

Внутренняя поперечная сила Q принимается положительной (т.е. Q>0), если она стремится повернуть рассматриваемую часть балки по ходу часовой стрелки.

Правило знаков для поперечной силы

При составлении уравнений равновесия рассматриваемых частей балки, правило знаков для внешних нагрузок (например сосредоточенной силы F) определяется аналогично.

Другими словами, внешние силы и распределенные нагрузки, стремящиеся повернуть рассматриваемую часть балки относительно рассматриваемого сечения по ходу часовой стрелки считаются положительными, и наоборот.

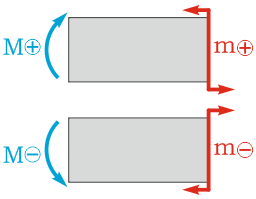
Правило знаков изгибающих моментов

Внутренний изгибающий момент M принимается положительным (т.е. M>0), если он стремится сжать верхние слои рассматриваемую части балки на рассматриваемом участке.

Правило знаков для изгибающего момента

Для внешних сосредоточенных моментов и моментов сил правило знаков аналогично, т.е. положительными считаются внешние моменты, сосредоточенные силы и распределенные нагрузки, сжимающие верхние слои балки.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

ПроСопромат.ру

Технический портал, посвященный Сопромату и истории его создания

Архив рубрики: Обозначения Сопромата

Изменения обозначений, принятых в сопромате, в соответствии с рекомендациями ИСО

Изменение русских индексов на латинские, соответствующие первым буквам аналогичного английского слова

Прочностные характеристики материала:

Напряжения:

Деформации:

Допускаемое значение величины обозначено не с помощью квадратных скобок, а с помощью индекса adm от англ. admissible — допускаемое

Применяемые индексы сокращений в сопромате

Применяемые индексы в обозначениях сопромата

Обозначения

Какие обозначения приняты в сопромате?

А – площадь поперечного сечения брутто, м 2 ;

а – размер стороны прямоугольника, м;

а – расстояние между параллельными осями, м;

а – длина силового участка, м;

а – ордината эпюры изгибающих моментов, Нм;

b – расстояние между параллельными осями, м;

b – ширина сечения, м;

b – ордината эпюры изгибающих моментов, Нм;

С – центр тяжести сечения;

с – размер сечения или его части, м;

с – длина силового участка, м;

с – ордината эпюры изгибающих моментов, Нм;

D – диаметр наружный сечения, м;

d– ордината эпюр изгибающих моментов, м;

d– диаметр внутренний сечения, м;

Е – модуль упругости I рода, модуль Юнга, Па;

F – сила, Н;

— 1 единичная сила, н;

G – модуль сдвига, Па;

g – ускорение свободного падения (м/с 2 );

Н – высота падения ударяющего тела, м;

I_x, I_y – осевые моменты инерции сечения, м 4 ;

I_ρ – полярный момент инерции сечения, м 4 ;

I_max, I_min – главные центральные моменты инерции сечения, м 4 ;

i – индекс у сил и усилий;

k_σ, k_τ– эффективные коэффициенты концентрации напряжений, безразмерные;

ℓ — длина стержня или силового участка, м;

М – сосредоточенный момент, Нм;

М_х, М_у – изгибающие моменты (внутренние), Нм;

М_к – крутящий момент (внутренний, может обозначаться Т (фр.)).

М_к, М_н – значения внутренних изгибающих моментов в конце и начале силового участка, Нм;

— единичная пара сил,

N – нормальная или продольная сила (внутренняя), н;

n – коэффициент запаса прочности (может быть обозначен как k);

[n] или n_adm – допускаемый коэффициент запаса прочности;

[n_уст ] или n_{уст adm}– допускаемый коэффициент запаса на устойчивость;

n_в – скорость вращения вала, об/мин;

Р – полное напряжение, Па;

Q (Q_x, Q_y) – поперечная сила (внутренняя), н;

q – погонная нагрузка, н/м;

q_σ,q_τ – коэффициенты чувствительности к концентрации напряжений, безразмерная;

R – равнодействующая сил, н;

S_x, S_y – статические моменты площади сечения, м 3 ;

t_i – усилие в ветви ремня (ременной передачи), н;

u – удельная потенциальная энергия деформирования;

u_р – удельная потенциальная энергия изменения формы;

u_max, u_min – главные центральные оси;

u – перемещение в направлении оси Х, м;

v – перемещение в направлении оси у, м;

v – скорость ударяющего тела. м/с 2 ;

w – перемещение в направлении оси z, м;

W_i – мощность, передаваемая шестерней, колесом и т.п., кВт;

W_x, W_y – осевые моменты сопротивления, м 3;

W_ρ – полярный момент сопротивления, м 3 ;

W_к – момент сопротивления при кручении, м 3 ;

х – горизонтальная ось сечения;

у – вертикальная ось сечения;

х₀, у₀ – центральные оси сечения;

y_max – координата точки, наиболее удаленной от нейтральной линии;

[σ] или σ_adm – допускаемое напряжение, Па;

σ_к – критическое напряжение, Па;

τ (τ_ху, τ_уz, τ_zx) – касательное напряжение, Па;

φ – угол поворота сечения при кручении, град;

φ – коэффициент понижения допускаемого напряжения, безразмерный;

α – угол, определяющий положение осей, град;

α₀ – угол, определяющий положение главных центральных осей, град;

β_σ β_τ – коэффициент, учитывающий влияние качества поверхности на усталость, безразмерная;

γ – удельный вес, н/м 3 ;

∆ – перемещение (линейное, м; угловое, рад);

∆ℓ – абсолютная линейная деформация (удлинение или укорочение), м;

∆b – абсолютная поперечная деформация, м;

∆S – абсолютный сдвиг, м;

ε – относительная линейная деформация, безразмерная;

ε_пр, ε_поп – относительные продольная и поперечная деформации, безразмерные;

ε_σ ε_τ – коэффициенты, учитывающие влияние размеров деталей на предел выносливости, безразмерные;

θ – относительный (погонный) угол поворота, рад/м;

λ – гибкость стержня, безразмерная;

μ – коэффициент Пуассона, безразмерная;

ν – коэффициент приведения длины, безразмерная;

σ (σ_х, σ_у, σ_z) – нормальное напряжение, Па;

σ₁, σ₂, σ₃ – главные напряжения, Па;

σ_пр или σ_pr– предел пропорциональности, Па;

σ_т илиσ_у – предел текучести, Па;

σ_пр или σ_u– предел прочности, Па.

Источник

Тема 2.2. Растяжение и сжатие

Под растяжением (сжатием) понимают такой вид нагружения, при котором в поперечных сечениях стержня возникают только продольные силы N, а прочие силовые факторы (поперечные силы, крутящий и изгибающий моменты) равны нулю.

Это самый простой и часто встречающийся вид деформации. Обычно он наблюдается когда внешняя нагрузка действует вдоль продольной оси стержня. Продольной осью стержня называется линия, проходящая через центры тяжести поперечных сечений.

Обычным является растяжение стержня силами, приложенными к его концам. Передача усилий к стержню может быть осуществлена различными способами, как это показано на рис. 1.

Рис. 1. Растяжение стержня

Во всех случаях, однако, система внешних сил образует равнодействующую F, направленную вдоль оси стержня. Поэтому независимо от условий крепления растянутого стержня, расчетная схема в рассматриваемых случаях (рис. 1, а, б) оказывается единой (рис. 1, в) согласно принципу Сен – Венана.

Если воспользоваться методом сечений (рис. 2), то становится очевидным, что во всех поперечных сечениях стержня возникают нормальные силы N_z, равные силе F (рис. 2, б).

Сжатие отличается от растяжения, формально говоря, только знаком силы N_z. При растяжении нормальная сила N_z направлена от сечения (рис. 2, б), а при сжатии – к сечению.

Рис. 2. Нормальная сила N

Растягивающие продольные силы принято считать положительными (рис. 3, а), а сжимающие – отрицательными (рис. 3, б).

Рис. 3. Знак продольной силы N

При расчете стержней, испытывающий деформацию растяжения, на прочность и жесткость при статическом действии нагрузки, надо решить две основные задачи. Это определение напряжений (от N_z), возникающих в стержне, и нахождение линейных перемещений в зависимости от внешней нагрузки.

Продольные силы (N_z), возникающие в поперечных сечениях стержня, определяются по внешней нагрузке с помощью метода сечений.

График, показывающий изменение продольных сил по длине оси стержня, называется эпюрой продольных сил (эп. N_z). Он дает наглядное представление о законе изменения продольной силы.

Осью абсцисс служит ось стержня. Каждая ордината графика – продольная сила (в масштабе сил) в данном сечении стержня.

Эпюра позволяет определить, в каком сечении действует максимальное внутреннее усилие (например, найти N_max при растяжении-сжатии). Сечение, где действует максимальное усилие будем называть опасным.

Перед построением эпюр необходимо освободить брус, в котором будем строить эпюры от опорных связей (выделить объект равновесия) и приложить к нему все действующие внешние силы (активные и реактивные). Затем необходимо установить границы участков, в пределах которых закон изменения внутренних сил постоянный. Границами таких участков являются сечения, где приложены сосредоточенные силы или начинается и кончается распределенная нагрузка, а также сечения, где имеется перелом стержня.

Применяя метод сечений и учитывая правила знаков изложенные выше, получаем уравнения изменения внутренних сил в пределах длины каждого участка бруса. Затем, используя, полученные зависимости строим графики (эпюры) этих усилий. Ординаты эпюр в определенном масштабе откладываем от базисной линии, которую проводим параллельно оси бруса.

На основании метода сечений продольная сила в произвольном поперечном сечении стержня численно равна алгебраической сумме проекций внешних сил, приложенных к стержню по одну сторону от рассматриваемого сечения, на его продольную ось.

Причем проекция внешней силы берется со знаком плюс, если сила растягивает часть стержня от точки ее приложения до рассматриваемого сечения и, наоборот, со знаком минус – если сжимает.

§2. Напряжение в поперечных сечениях стержня

Продольная сила N с помощью метода сечений всегда может быть выражена через внешние силы. В формулe следует подставлять алгебраическое значение N т.е со знаком плюс в случае растяжения и со знаком минус в случае сжатия

§3. Расчеты на прочность и жесткость при растяжении-сжатии

Прочность стержня при осевом растяжении и сжатии обеспечена, если для каждого его поперечного сечения наибольшее расчетное (рабочее) напряжение σ не превосходит допускаемого [σ] : σ=N/A≤ [σ],

Данное выражение определяет условие прочности при растяжении или сжатии.

С помощью этой формулы решается три вида зада (выполняется три вида расчета):

1. Проверка прочности (проверочный расчет). При заданных продольной силы N и площади поперечного сечения А определяют рабочее (расчетное) напряжение и сравнивают его с допускаемым [σ].

В случаях, когда рабочее напряжения значительно ниже допускаемых σ

Источник

iSopromat.ru

Правила знаков для внешних сил, моментов, внутренних силовых факторов, напряжений и перемещений принятые в сопромате, теоретической и технической механике при решении задач.

Правила знаков для внутренних силовых факторов

При растяжении-сжатии

Внутренняя продольная сила N, которая стремится растянуть рассматриваемую часть бруса, считается положительной. Сжимающая продольная сила имеет отрицательный знак.

Положительное направление внутренней продольной силы N

Подборка видео по всем правилам знаков:

При кручении

Внутренний скручивающий момент T считается положительным, если он стремится повернуть рассматриваемую часть бруса против хода часовой стрелки, при взгляде на него со стороны внешней нормали.

Положительное направление внутреннего скручивающего момента T

При изгибе

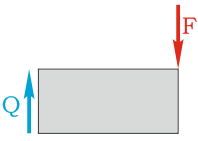
Внутренняя поперечная сила Q считается положительной, в случае, когда она стремится повернуть рассматриваемую часть бруса по ходу часовой стрелки.

Положительное направление внутренней поперечной силы Q

Внутренний изгибающий момент M положителен, когда он стремится сжать верхние волокна бруса.

Положительное направление внутреннего изгибающего момента M

Примечание: Величина и знак внутренних сил и моментов зависит от вызывающих их внешних усилий, поэтому указанные правила знаков в том же виде справедливы и для внешних нагрузок.

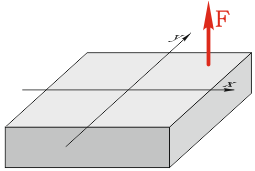
Правило знаков при внецентренном нагружении

Положительными принимаются внешние усилия стремящиеся вызвать растяжение первой четверти сечения.

Положительное направление действия внешних нагрузок

Правила знаков для напряжений

Нормальные напряжения σ положительны, если они растягивают выделенный элемент бруса.

Положительные нормальные напряжения

Касательные напряжения τ будут положительными, если они стремятся повернуть рассматриваемый элемент бруса по ходу часовой стрелки.

Положительные касательные напряжения

Правило знаков для деформаций и перемещений

Деформация при растяжении-сжатии Δl считается положительной, если длина стержня при этом увеличивается.

Положительная деформация при продольном нагружении

При плоском поперечном изгибе

Вертикальное перемещение сечения бруса принимается положительным, если оно направлено вверх от начального положения.

Положительные перемещения сечений балки при изгибе

Правило знаков при составлении уравнений равновесия

Для проекций сил на оси системы координат

Проекции внешних сил на оси системы координат принимаются положительными, если их направление совпадает с положительным направлением соответствующей оси.

Для моментов

Сосредоточенные моменты и моменты сил в уравнениях статики записываются с положительным знаком, если они стремятся повернуть рассматриваемую систему против хода часовой стрелки.

Правило знаков при составлении уравнений статики для неподвижных систем

При составлении уравнений равновесия статичных (неподвижных) систем (например, при определении опорных реакций), последние два правила упрощаются до вида:

Проекции сил и моменты, имеющие одинаковое направление записываются с одинаковыми знаками, соответственно проекции сил и моменты обратного направления – с противоположными.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник