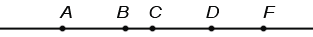Что такое дерево вариантов в математике

Комбинаторные задачи

Метод перебора

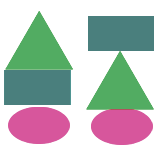
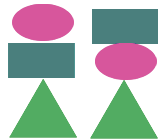
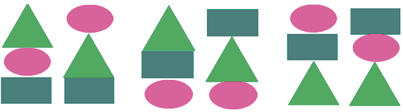
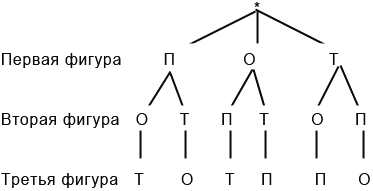
Итак, мы получили шесть возможных вариантов:

Ответ: 6 способов.

Дерево возможных вариантов

Метод отрезков

Данный метод используется только для составления всевозможных пар. Например, рассмотрим прямую, на которой обозначены точки A, B, C, D, F:

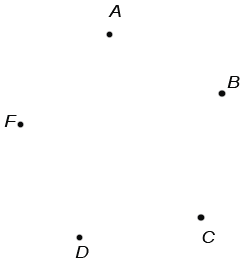
Необходимо ответить на вопрос: » Сколько отрезков изображено на рисунке?». Мы знаем, что отрезок обозначается двумя буквами, значит, для ответа на вопрос необходимо перебрать всевозможные пары букв. Это можно сделать при помощи следующей схемы: Отметим точки так, чтобы никакие 3 не лежали на одной прямой:

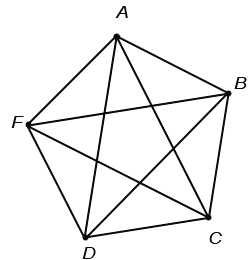
Соединим данные точки отрезками между собой. Число отрезков будет числом вариантов, то есть числом отрезков, изображенных на рисунке:

Итак, мы получили 10 отрезков, соединяющих точки.

Ответ: На рисунке 10 отрезков.

Поделись с друзьями в социальных сетях:

Источник

Урок алгебры по теме: » Дерево возможных вариантов».

Урок 70. Дерево возможных вариантов.

Цели: изучить комбинаторное правило умножения; формировать умения решать комбинаторные задачи с помощью правила умножения и составления таблиц возможных вариантов.

I. Организационный момент.

1. Три друга при встрече обменялись рукопожатиями. Сколько всего было сделано рукопожатий? (3.)

2. Есть помидоры, огурцы и лук. Сколько различных салатов можно приготовить, если в каждый из них должны входить в равных долях 2 различных вида овощей? (3.)

3. Перечислить все возможные способы разложения по двум вазам одного яблока и одной груши. (4.)

4. Сколькими способами Петя и Вова могут занять 2 места за одной двухместной партой? (2.)

5. Сколько подарочных наборов можно составить:

1) из одного предмета; (1.)

2) из двух предметов, если в наличии имеются одна ваза и одна ветка сирени? (3.)

III. Объяснение нового материала.

1. Чтобы подвести учащихся к «открытию» комбинаторного правила умножения, целесообразно начать объяснение нового материала с проверки решения задачи № 714 (домашнее задание) с выносом графа-дерева решения на доску:

Замечаем, что можно было решить эту задачу даже устно. Рассуждаем так. Первое блюдо можно выбрать двумя способами. Для каждого первого блюда можно подобрать второе четырьмя способами. Эти выборы независимы друг от друга, так как каждый осуществляется из своего множества вариантов. Значит, общее число вариантов обеда равно произведению 2 · 4, то есть 8.

В о п р о с у ч а щ и м с я: а если бы на обед было предложено выбрать еще одно третье блюдо из пяти: чай, кофе, сок, компот, кисель? Тогда для каждого варианта обеда мы могли бы предложить пять вариантов третьего блюда и получили бы 8 · 5 или 40 вариантов обеда из трех блюд.

Формулируем его в общем виде, обращая особое внимание на условие его применения – выбор из независимых наборов вариантов:

3. П р и м е р 3 рассматриваем из учебника со с. 173.

IV. Формирование умений и навыков.

На прошлом уроке мы рассмотрели два способа решения комбинаторных задач:

1. Перечисление (полный перебор) вариантов.

2. Подсчет вариантов с помощью графов.

2.2. Дерево возможных вариантов (граф-дерево).

На этом уроке добавляются еще два способа:

3. Составление таблицы возможных вариантов.

4. Непосредственное применение комбинаторного правила умножения.

№ 727, № 728. На непосредственное применение комбинаторного правила умножения.

О б р а з е ц о ф о р м л е н и я решения задачи.

В задаче 4 последовательных выбора, каждый из своего множества вариантов. Общее количество различных карнавальных костюмов равно:

О т в е т: 180 различных костюмов.

Выбирая команды для игры, мы не учитываем порядок в паре, так как если первая команда играла со второй, то это одновременно означает, что вторая команда играла с первой.

Составим таблицу возможных вариантов, отмечая крестиком игру между командами.

.

Это мы посчитали количество игр, проведенных командами на своем поле. Значит, столько же игр сыграно на поле противника. Итого – 132 игры.

На прошлом уроке мы решали такую же задачу, но с меньшим количеством участников, с помощью графа. В этой задаче этот способ применять нецелесообразно, так как очень большое количество ребер графа может только запутать учеников. Покажем два других способа решения этой задачи.

I с п о с о б. Составление таблицы возможных вариантов.

( а _п ) – арифметическая прогрессия.

О т в е т: 28 рукопожатий.

II с п о с о б. Применение комбинаторного правила умножения.

Каждый человек пожимает руку семи оставшимся. Но так как порядок выбора не имеет значения (если Иванов пожимает руку Петрову, то одновременно и Петров пожимает руку Иванову), то общее число рукопожатий равно = 28.

О т в е т: 28 рукопожатий.

№ 725. Применение комбинаторного правила умножения.

Всего 10 цифр, каждая цифра комбинируется с оставшимися девятью (причем важен порядок, так как 2–3 и 3–2 разные коды) и с самой собой (возможен код 1–1, 3–3 и т. д.). Значит, вариантов 10 · 10 = 100. Так как в доме 96 квартир, то кодов хватит для всех.

В о п р о с ы у ч а щ и м с я:

– Какие способы решения комбинаторных задач вы знаете?

– Охарактеризуйте каждый способ решения.

– Сформулируйте комбинаторное правило умножения.

Домашняя работа: № 724, № 726, № 834, № 730 (а), № 731 (в).

Источник

Презентация на тему «Комбинаторные задачи. Дерево возможных вариантов»

Описание презентации по отдельным слайдам:

Комбинаторные задачи: дерево возможных вариантов

ИМЯ УРОКА: КОМБИНАТОРИКА ДЕВИЗ УРОКА: «УСЛЫШАЛ – ЗАБЫЛ, УВИДЕЛ – ЗАПОМНИЛ, СДЕЛАЛ – ПОНЯЛ» КИТАЙСКАЯ ПОГОВОРКА

В странных русских сказаниях повествуется, как богатырь или другой добрый молодец, доехав до распутья, читает на камне: Вперёд поедешь – голову сложишь. Налево поедешь – меча лишишься. А дальше говорится, как он выходит из того положения, в которое попал в результате выбора. Направо поедешь – коня потеряешь. Но выбирать разные пути или варианты приходится и современному человеку. Эти пути и варианты складываются в самые разнообразные комбинации.

Что такое КОМБИНАТОРИКА? Задачи, в которых требуется осуществить перебор всех возможных вариантов, или, как обычно говорят в таких случаях, всех возможных комбинаций, называют комбинаторными. Область математики, изучающая комбинаторные задачи, называется комбинаторикой. Комбинаторика – раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчинённых тем или иным условиям, можно составить.

Задача №1 Запишите все трёхзначные числа, для записи которых употребляются только цифры 1 и 2. 1 2 1 1 2 2 1 1 1 1 2 2 2 2 Ответ: 111, 112, 121, 122, 211, 212, 221, 222 – восемь чисел. Такой метод решения комбинаторных задач называется деревом выбора(дерево возможных вариантов)

Задача №2 Запишите все трёхзначные числа, для записи которых употребляются только цифры 0,7.

ЗАДАЧА 3 В 5 «А» классе в среду 4 урока: математика, информатика, русский язык, английский язык. Сколько можно составить вариантов расписания на среду? Решение: построим картину-схему. Для удобства закодируем названия предметов: математика – м, информатика – и, русский язык – р, английский язык – а.

РЕШЕНИЕ ЗАДАЧИ 3 Расписание 1 урок м и р а 2 урок и р а м р а м и а м и р 3 урок р а и а и р р а м а м р и а м а м и и р м р м и 4 урок а р а и р и а р а м р м а и а м и м р и р м и м Ответ: 24 варианта: мира, миар, мриа, мраи, маир, мари, имра, имар, ирма, ирам, иамр, иарм, рмиа, рмаи, рима, риам, рами, раим, амир, амри, аимр, аирм, арми, арим.

Построенная схема напоминает перевернутое дерево: от ствола («расписание») отходят ветки, сначала четыре (м, и, р, а), от каждой из четырех веток – еще по три, затем еще по две и еще по одной. Видимо поэтому такую схему называют деревом возможных вариантов. Дерево возможных вариантов можно считать геометрической моделью рассматриваемой ситуации.

Можно решить Задачу 3 короче, если применить правило умножения. Существует 4 варианта выбора первого урока. Для выбора второго урока есть только три варианта, так как один из четырех уроков мы уже выбрали. Тогда для третьего урока существует два варианта, а для четвертого только один. Применив правило умножения, получим 4 ∙ 3 ∙ 2 ∙1= 24 Ответ: 24 варианта.

Задача №5 В классе 15 мальчиков и 10 девочек. Сколькими способами можно выбрать двух дежурных(одну девочку и одного мальчика)?

ЗАДАЧА 2. В 6 классе в четверг 5 уроков: математика, информатика, русский язык, английский язык, физкультура. а) Сколько имеется вариантов расписания при условии, что физкультура – последний урок? б) Сколько имеется вариантов расписания при условии, что физкультура – последний урок, а математика – первый?

ЗАДАЧА 2 (ПРОДОЛЖЕНИЕ). В 6 классе в четверг 5 уроков: математика, информатика, русский язык, английский язык, физкультура. в) Сколько всего можно составить вариантов расписания на четверг? г) Сколько времени потратит завуч на запись всех вариантов, если известно, что на запись одного варианта у него уходит 30 секунд?

Задача №1 Запишите все трёхзначные числа, для записи которых употребляются только цифры 0,7. Задача №2 Сколько двузначных чисел можно составить, используя цифры 1, 4 и 7? Нарисуйте дерево выбора на альбомном листе. Задача №3 Составьте комбинаторную задачу, которая решается с помощью правила умножения. Сделайте к ней рисунок. Задача № 4 Тренер попросил Филю составить трехзначное число из цифр 1, 2, 3, 4, причем цифры в числе могут повторяться. Сколько чисел может составить Филя? Задача № 5 Тренер попросил Филю составить трехзначное число из цифр 1, 2, 3, 4 так, чтобы цифры в числе не повторялись. Сколько чисел может составить Филя? Домашнее задание

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-409677

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В российских школах могут появиться «службы примирения»

Время чтения: 1 минута

Минздрав включил вакцинацию подростков от ковида в календарь прививок

Время чтения: 1 минута

Рособрнадзор разрешил провести ВПР по некоторым предметам на компьютерах

Время чтения: 0 минут

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

В России утвердили новый порядок формирования федерального перечня учебников

Время чтения: 1 минута

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Методы решения комбинаторных задач

Методы решения комбинаторных задач

Перебор возможных вариантов

Простые задачи решают обыкновенным полным перебором возможных вариантов без составления различных таблиц и схем.

Задача 1.
Какие двузначные числа можно составить из цифр 1, 2, 3, 4, 5?

Ответ: 11, 12, 13, 14, 15, 21, 22, 23, 24, 25, 31, 32, 33, 34, 35, 41, 42, 43, 44, 45, 51, 52, 53, 54, 55.

Задача 2.
В финальном забеге на 100 м участвуют Иванов, Громов и Орлов. Назовите возможные варианты распределения призовых мест.

Ответ:
Вариант1: 1) Иванов, 2) Громов, 3) Орлов.
Вариант2: 1) Иванов, 2) Орлов, 3) Громов.
Вариант3: 1) Орлов, 2) Иванов, 3) Громов.
Вариант4: 1) Орлов, 2) Громов, 3) Иванов.
Вариант5: 1) Громов, 2) Орлов, 3) Иванов.
Вариант6: 1) Громов, 2) Иванов, 3) Орлов.

Задача 3.
В кружок бального танца записались Петя, Коля, Витя, Олег, Таня, Оля, Наташа, Света. Какие танцевальные пары девочки и мальчика могут образоваться?

Дерево возможных вариантов

Задача 4.
Какие трехзначные числа можно составить из цифр 0, 2, 4?

Решение. Построим дерево возможных вариантов, учитывая, что 0 не может быть первой цифрой в числе.

Ответ: 200, 202, 204, 220, 222, 224, 240, 242, 244, 400, 402, 404, 420, 422, 424, 440, 442, 444.

Ответ: На рисунке перечислены все 12 возможных вариантов путешествия школьных туристов.

Задача 6.
Запишите все возможные варианты расписания пяти уроков на день из предметов: математика, русский язык, история, английский язык, физкультура, причем математика должна быть вторым уроком.

Ответ: Всего 24 возможных варианта:

Источник

Тема урока: Правило умножения и дерево возможных вариантов

Преподаватель математики ПУ № 11

Тема урока: Правило умножения и дерево возможных вариантов.

— научить учащихся подсчитывать количество возможных вариантов по правилу умножения;

— воспитывать внимательность и умение анализировать результаты.

б)позволяет всё учесть, ничего не пропустив.

Задача №1. Составить двузначные числа из цифр 2,5 и 9.

первая цифра 2 5 9

Подсчитаем количество решений по правилу умножения:3×3=9

Волгоград

Нижний Новгород т п

Москва с т п а с т п а

Варианты путешествия: тс, тт, тп, та, пс, пт, пп, па.

Таким образом, имеется 8 возможных способов добраться из Волгограда в Нижний Новгород, а затем в Москву. Из них можно выбрать подходящий по времени и стоимости.

По правилу умножения: 2×4=8.

Задача №3. В палатке имеется три сорта мороженого: рожок (р), брикет (б), эскимо (э). Маша и Саша решили купить по одной порции. Сколько вариантов такой покупки существует?

Выбор Саши б р э б р э б р э

Варианты покупки: бб, бр, бэ, рб, рр, рэ, эб, эр, ээ.

Таким образом, имеется 9 вариантов покупки мороженого.

По правилу умножения: 3×3=9.

В-1. Пусть Маша хочет купить себе две порции мороженого.

(В решении варианты бр и рб, бэ и эб, рэ и эр одиноковы. Остаётся 6 вариантов)

В-2. Пусть Маша хочет купить две порции разного сорта мороженого.

В решении варианты бб, рр, ээ не подходят. Остаётся 3 варианта)

Задача №4. Данила, Андрей и Наташа собрались потренироваться в бросании мяча в баскетбольную корзину. У них только один мяч, и им надо договориться, кто за кем будет бросать мяч. Сколькими способами они могут занять очередь друг за другом?

Первый Н Д А

Второй Д А Н А Н Д

Третий А Д А Н Д Н

Варианты очереди: НДА, НАД, ДНА, ДАН, АНД, АДН.

Таким образом, у ребят имеется 6 различных вариантов очереди.

По правилу умножения: 3×2=6.

Ф 1 ф 2 ф 3 ф 4

Ш1 ш2 ш3 ш1 ш2 ш 3 ш1 ш2 ш3 ш1 ш 2 ш3

Есть варианты нарядов для мишки: ф1ш1, ф1ш2, ф1ш3, ф2ш1, ф2ш2, ф2ш3, ф3ш1, ф3ш2, ф3ш3,ф4ш1, ф4ш2, ф4ш3. Всего 12 вариантов.

Получается, что у мишки больше нарядов.

Задача №6. Составить дерево вариантов для решения задачи.

В коридоре три лампочки. Сколько имеется различных способов освещения коридора?

+ _

Вторая вторая

Третья третья третья третья

Можно решить задачу с помощью правила умножения.

Теперь сформулируем правило умножения:

Для того, чтобы найти число всех возможных исходов независимого проведения двух испытаний А и В, следует перемножить число всех исходов испытаний А и число всех исходов испытаний В.

Задача №7. Сколько четных двузначных чисел можно составить из цифр 0,1,2,4,5,9? Решить задачу с помощью правила умножения.

(Всего 15 чисел. 5×3=15)

3. Итог занятия. ( о значении использования дерева вариантов при решении комбинаторных задач).

4. Задание на дом. Составить задачу по профессии, при решении которой используется дерево вариантов.

Источник