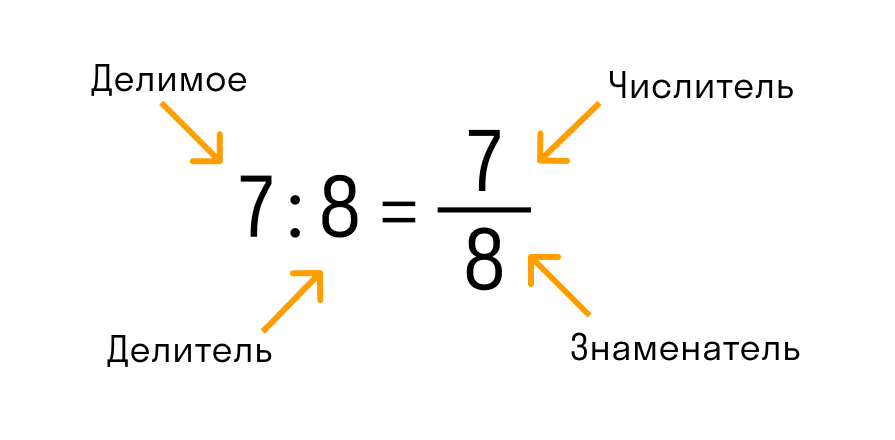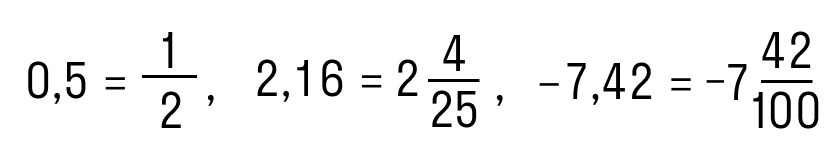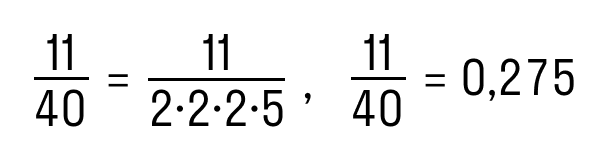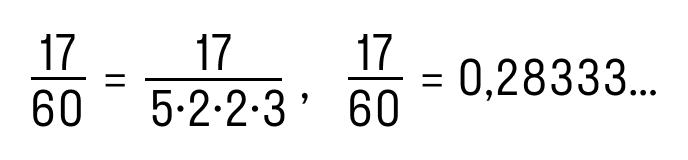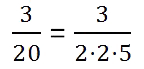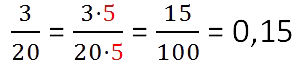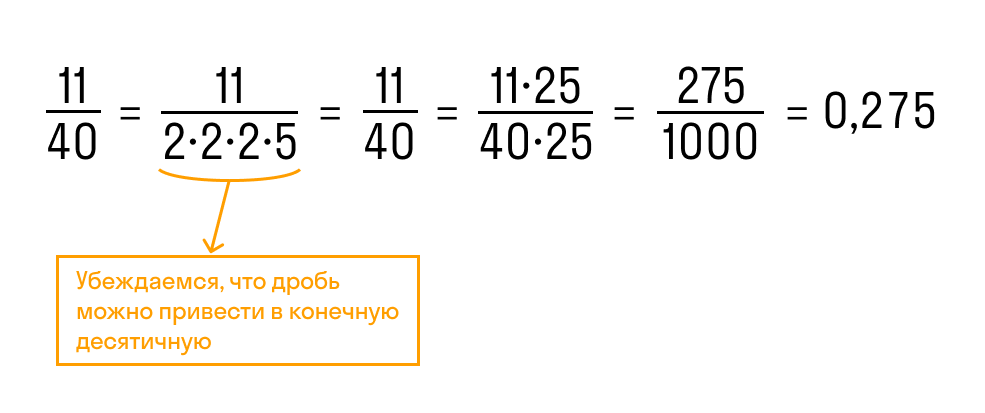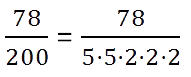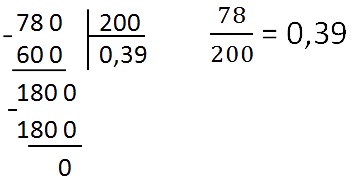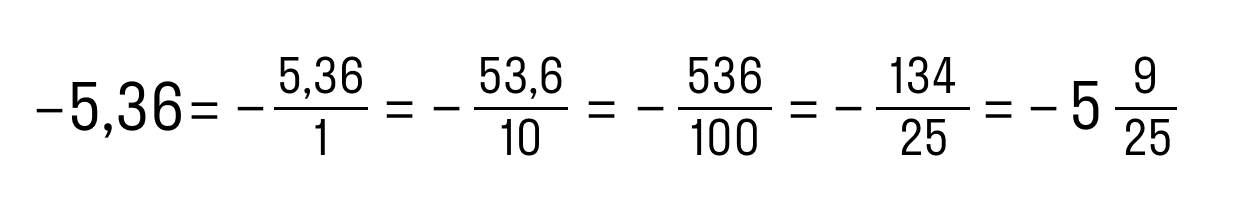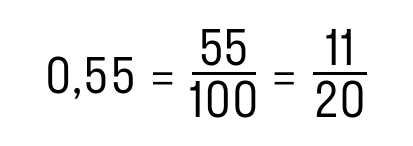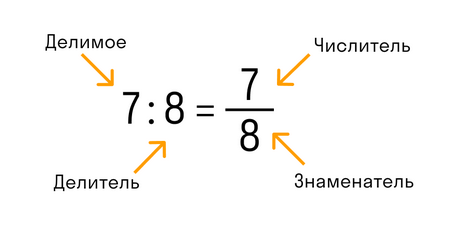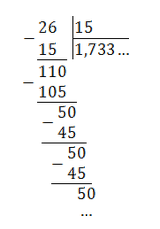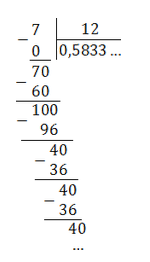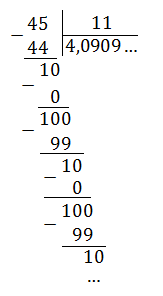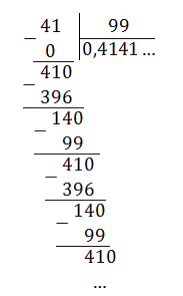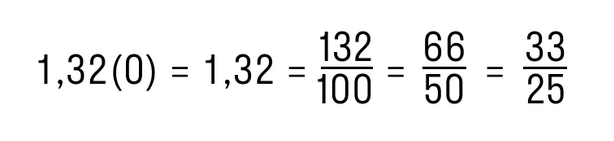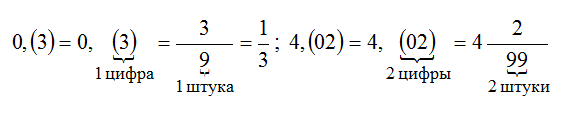Что такое десятичное разложение обыкновенной дроби
Алгебра. 7 класс
Конспект урока
Периодические десятичные дроби. Периодичность десятичного разложения обыкновенной дроби
Перечень рассматриваемых вопросов:
Понятие бесконечной периодической десятичной дроби.
Примеры бесконечной периодической десятичной дроби.
Представление рационального числа в видебесконечной периодической десятичной дроби.
Любое целое число и любую конечную десятичную дробь можно считать бесконечной периодической десятичной дробью или коротко: периодической дробью.
Любое положительное рациональное число
преобразуется в положительную дробь.
Любая периодическая дробь – это десятичное разложение некоторого положительного рационального числа
Если в периодической дроби период начинается сразу после запятой, то такую периодическую дробь называют «чистой».
Если в периодической дроби период начинается не сразу, а после некоторого количества не повторяющихся цифр, то такую периодическую дробь называют «смешанной».
1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.
1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.
2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.
3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.
Теоретический материал для самостоятельного изучения.
На прошлом уроке мы рассмотрели условия, при которых обыкновенную дробь можно представить в виде конечной десятичной.
А как поступать, когда невозможно представить её в таком виде?
Введём понятие бесконечной периодической десятичной дроби.
Если знаменатель q несократимой дроби p/q не имеет делителей, кроме 2 и 5, то эта дробь преобразуется в конечную десятичную дробь.
Если знаменатель содержит, кроме 2 и 5, другие простые делители, то мы не сможем представить её конечной десятичной дробью.
Знаменатель 9 = 3 3
5/9 не преобразуется в конечную десятичную дробь. Убедимся в этом, выполнив деление уголком.
Разделим числитель 5 на знаменатель 9.
Процесс деления в столбик бесконечный. Приходим к выражению 0,555…,
точки означают, что цифра 5 периодически повторяется бесконечно много раз.
Выражение 0,555… называют бесконечной периодической десятичной дробью или коротко: периодической дробью.
Читают: « ноль целых и пять в периоде».
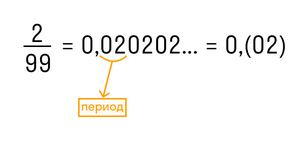
Цифру (5) называют периодом дроби 0,(5).
Говорят, что число пять девятых представлено в виде периодической дроби ноль целых и пять в периоде.
Выражение 5/9 и 0,(5) являются обозначениями одного и того же числа в виде обыкновенной дроби 5/9 и в виде периодической дроби 0,(5).
Рассмотрим ещё пример.
Дробь четыре пятнадцатых несократимая, и её знаменатель имеет простые делители 3 и 5, поэтому деление не может быть конечным. Проверим.
Делим уголком 4 на 15.
читают: «ноль целых две десятых и шесть в периоде».
В примерах мы увидели разные периодические дроби.
Периодические дроби бывают двух видов: «чистые» и «смешанные».
Если в периодической дроби период начинается сразу после запятой, то такую периодическую дробь называют «чистой».
Видно, что в этих дробях период начинается сразу после запятой.
Если же в периодической дроби период начинается не сразу, а после некоторого количества не повторяющихся цифр, то такую периодическую дробь называют «смешанной».
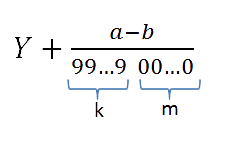
Если применить правило деления уголком к любой несократимой дроби p/q
Где q – знаменатель, который, кроме 2 и 5 имеет другие простые делители, то получится бесконечная периодическая десятичная дробь, или коротко: периодическая дробь.
Приписывая к конечной десятичной дроби бесконечно много нулей, мы её приводим в бесконечную периодическую десятичную дробь с периодом 0.
45 = 45,0 = 45,000… = 45,(0)
0,673 = 0,673000 = 0,673(0).
Значит, любое целое число и любую конечную десятичную дробь можно считать бесконечной периодической десятичной дробью или коротко: периодической дробью.
Любое положительное рациональное число p/q преобразуется в периодическую дробь.
Верно обратное. Любая периодическая дробь – это десятичное разложение некоторого положительного рационального числа p/q.
Периодичность десятичного разложения обыкновенной дроби
Рассмотрим произвольную положительную несократимую дробь p/q
Покажем, что если разделить числитель дроби на знаменатель уголком, то в частном получится либо конечное, либо бесконечное периодическое её преобразование.
Нам известно, чтобы получить конечное десятичное разложение, знаменатель qне должен иметь простых делителей, кроме 2 и 5
В других случаях может быть только бесконечное десятичное разложение, которое является периодическим. Пусть нужно найти десятичное разложение несократимой дроби 15/13.
Будем делить уголком 15 на 13.
Здесь одной звёздочкой отмечен этап вычислений, когда снесена последняя цифра делимого. Получаемые после этого остатки заключены в прямоугольники. Видно, что остатки, отмеченные двумя, тремя звёздочками, равны между собой. Это показывает, что процесс деления носит периодический характер и приводит к бесконечной периодической десятичной дроби, то есть:
Теперь на примере рассмотрим, как можно, зная бесконечную периодическую десятичную дробь, записать её обыкновенной дробью.
Запишем периодическую дробь 0,(7) в виде обыкновенной.
Для этого обозначим искомую величину х. Тогда справедливо равенство
Умножим это равенство на 10, получим
Вычтем из равенства (2) равенство (1).
Применив к дроби 7/9 деление уголком. Снова получим периодическую дробь 0, (7.)
Разбор заданий тренировочного модуля.
Подберите обыкновенную дробь, равную периодической десятичной 0,(14).
Варианты ответов: 14/99, 14/98 14/90
Обозначим искомую величину х. Тогда справедливо равенство:
Умножим это равенство на 100, получим
Вычтем из равенства (2) равенство (1).
Найдите десятичное разложение обыкновенной дроби 769/4950
Решение: Для решения задачи нужно выполнить деление уголком:
Алгебра. 7 класс
Конспект урока
Разложение обыкновенной дроби в конечную десятичную дробь
Перечень рассматриваемых вопросов:
— Описание соотношений между десятичными и обыкновенными дробями.
— Формулировка признака обратимости обыкновенной дроби в десятичную. Применение его для распознавания дробей, для которых возможна (или невозможна) десятичная запись.
— Представление обыкновенных дробей в виде десятичных.
Конечная десятичная дробь, записанная в виде обыкновенной несократимой дроби виде p/q, будет иметь знаменатель q, который не имеет простых делителей кроме 2 и 5.
Чтобы записать обыкновенную несократимую дробь в виде десятичной дроби, нужно и числитель, и знаменатель умножить на одно и то же число, так, чтобы в знаменателе получилось 10, 100, 1000 и т. д.
Чтобы перевести обыкновенную дробь в десятичную, нужно числитель разделить на знаменатель.
1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.
1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.
2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.
3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.
Теоретический материал для самостоятельного изучения.
Сегодня на уроке расширим наши знания о возможности записи обыкновенной дроби в виде десятичной дроби.
Нам известно, что конечную десятичную дробь всегда можно записать в виде обыкновенной несократимой дроби.
Видим, что после сокращения дробей получились знаменатели, которые не имеют простых делителей, кроме 2 и 5.
Из рассмотренных нами примеров можно увидеть, что если конечную десятичную дробь записать в
делителей кроме 2 и 5.
Верно и обратное утверждение.
можно записать в виде конечной десятичной дроби.
Для записи обыкновенной несократимойдроби, знаменатель которой не имеет других простых делителей, кроме 2 и 5, в виде конечной десятичной, существует два способа.
Первый способ перевода
Чтобы перевести обыкновенную дробь в десятичную, нужно и числитель, и знаменатель умножить на одно и то же число, так, чтобы в знаменателе получилось 10, 100, 1000 и т. д.
Но сначала, нужно проверить, можно ли привести обыкновенную дробь в десятичную.
Умножаем числитель и знаменатель на 625. В знаменателе получим 10000.
Второй способ перевода.
Для того, чтобы его использовать, нужно вспомнить деление уголком.
Чтобы перевести обыкновенную дробь в десятичную, нужно числитель разделить на знаменатель.
Убеждаемся, что дробь можно перевести в конечную десятичную.
Делим уголком числитель на знаменатель.
Видно, что оба способа разложения привели к одной и той же десятичной дроби.
Таким образом, на этом уроке мы узнали:
— при каких условиях можно привести обыкновенную дробь в десятичную;
— два способа перевода обыкновенной дроби в десятичную.
Видим, что дробь несократимая. Проверим, какие простые делители присутствуют в знаменателе.
Разложим 800 на простые множители.
Значит, можно представить в виде обыкновенной дроби.
Теперь разделим уголком числитель на знаменатель и получим.
№ 1. Выделите цветом правильный ответ.
Решение: Для решения задачи, нужно разделить столбиком 651 на 2000
Как перевести дробь в десятичную и наоборот
Что такое дробь: понятие
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которой можно представить число. Есть два формата записи:
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
Дроби бывают двух видов:
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 3/7 и 31/45.
Неправильной — ту, у которой числитель больше знаменателя или равен ему. Например, 21/4. Такое число является смешанным и читается, как «пять целых одна четвертая», а записывается — 5 1\4.
Что такое десятичная дробь
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
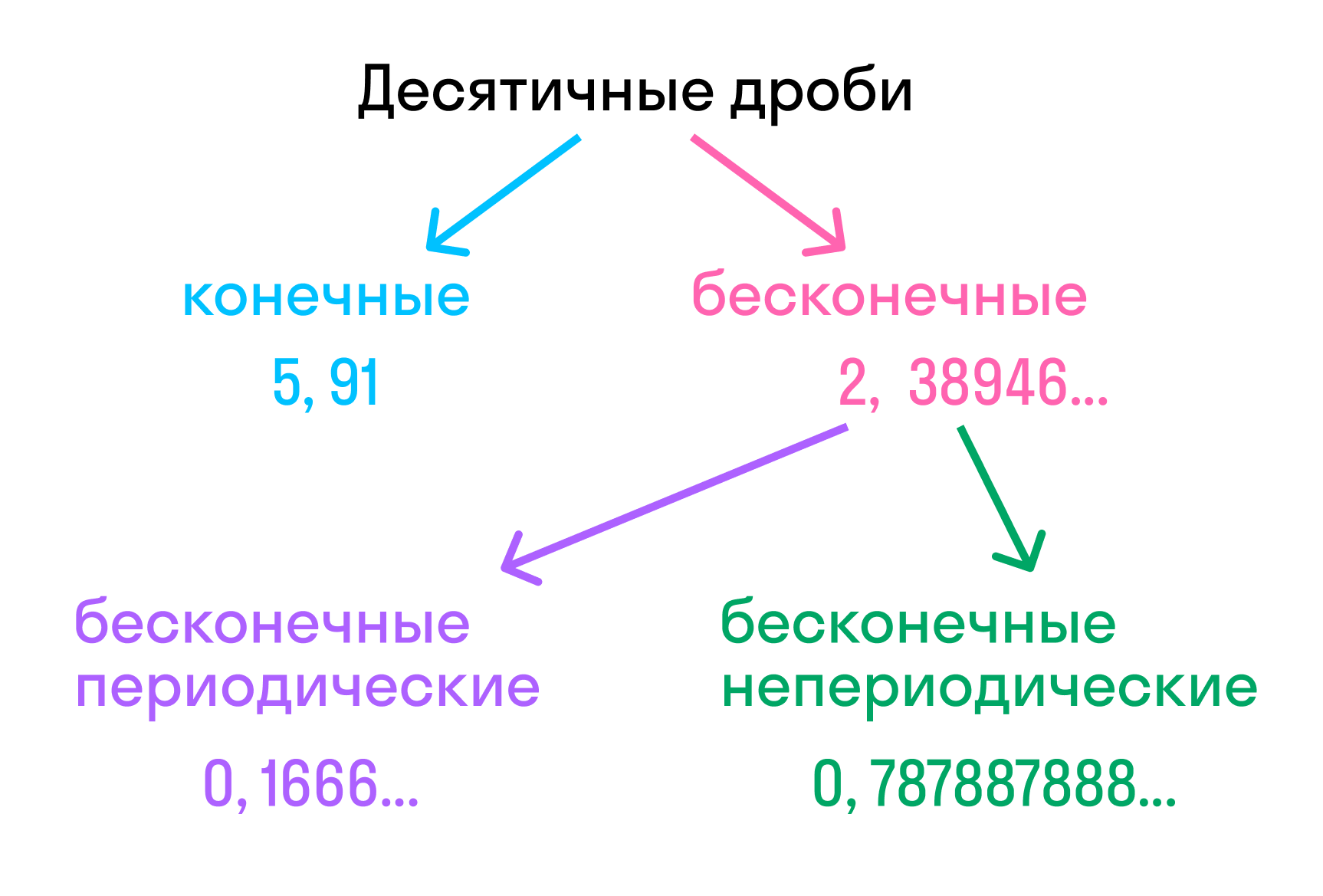
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
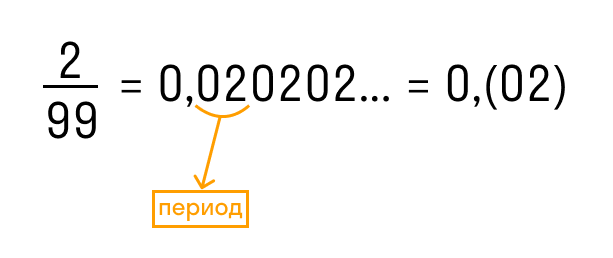
В краткой записи периодической дроби повторяющиеся цифры пишут в скобках и называют периодом дроби. Например, вместо 1,555… записывают 1,(5) и читают «одна целая и пять в периоде».
Обучение на курсах математики в Skysmart поможет улучшить оценки в школе и подготовиться к выпускным экзаменам!
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
Обыкновенная и десятичная дробь — давние друзья. Вот как они связаны:
Как перевести обычную дробь в десятичную
Прежде чем узнать, как от обычной записи перейти к десятичной, вспомним различия двух видов дробей и сформулируем важное правило.
Обыкновенную дробь можно перевести в конечную десятичную дробь только при условии, что её знаменатель можно разложить на простые множители 2 и 5 любое количество раз. Например:
Дробь 11/40 можно преобразовать в конечную десятичную, потому что знаменатель раскладывается на множители 2 и 5.
Дробь 17/60 нельзя преобразовать в конечную десятичную дробь, потому что в её знаменателе кроме множителей 2 и 5, есть 3.
А теперь перейдем к самому главному вопросу: рассмотрим несколько алгоритмов перевода обыкновенной дроби в десятичную.
Способ 1. Превращаем знаменатель в 10, 100 или 1000
Чтобы превратить дробь в десятичную, нужно числитель и знаменатель умножить на одно и то же число так, чтобы в знаменателе получилось 10, 100, 1000 и т.д. Но прежде, чем приступать к вычислениям, нужно проверить, можно ли вообще превратить данную дробь в десятичную.
Для примера возьмем дробь 3/20. Ее можно привести в конечную десятичную, потому что её знаменатель раскладывается на множители 2 и 5.
Мы можем получить в нижней части 100: достаточно умножить 20 на 5. Про верхнюю часть тоже не забываем: получаем 15.
Теперь запишем числитель отдельно. Отсчитываем справа столько же знаков, сколько нулей стоит в знаменателе, и ставим запятую. В нашем примере в знаменателе 100 (у него два нуля), значит ставим запятую после отсчета двух знаков и получаем 0,15. Преобразование готово.
Способ 2. Делим числитель на знаменатель
Чтобы перевести обыкновенную дробь в десятичную, достаточно разделить ее верхнюю часть на нижнюю. Проще всего это сделать, конечно же, на калькуляторе — но на контрольных им пользоваться не разрешают, поэтому учимся по-другому.
Для примера возьмем дробь 78/100. Убедимся, что дробь можно привести в конечную десятичную.
Делим столбиком числитель на знаменатель — преобразование готово:
Если при делении уголком стало ясно, что процесс не заканчивается и после запятой выстраиваются повторяющиеся цифры — эту дробь нельзя перевести в конечную десятичную. Ответ можно записать в виде периодической дроби — для этого нужно записать повторяющееся число в скобки, вот так: 1/3 = 0,3333.. = 0,(3).
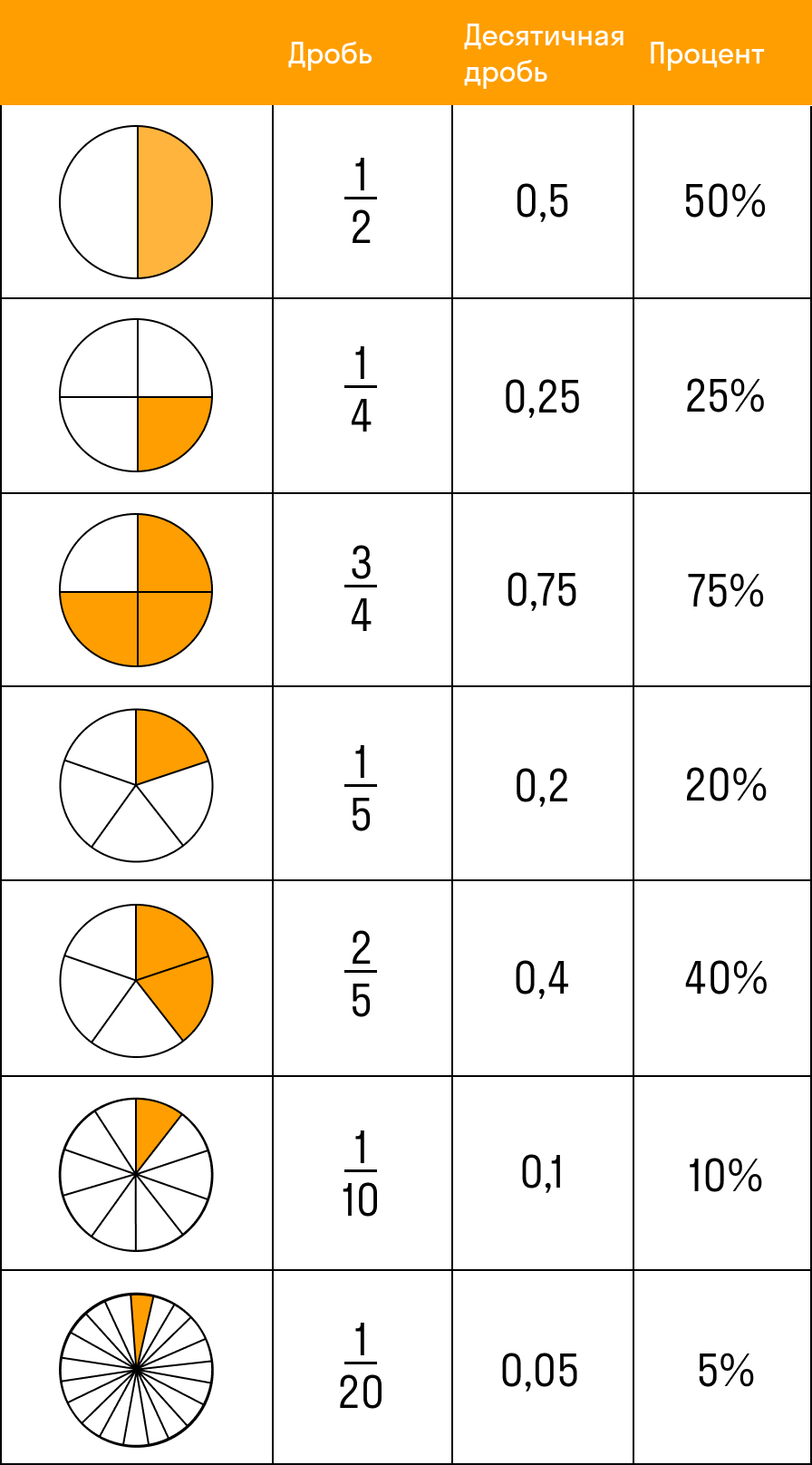
Для удобства мы собрали табличку дробей со знаменателями, которые чаще всего встречаются в заданиях по математике. Скачайте ее на гаджет или распечатайте и храните в учебнике как закладку:
Как перевести десятичную дробь в обыкновенную
Не будем придумывать велосипед. По сути, алгоритм превращения десятичной дроби в обыкновенную противоположен тем, что мы разобрали в предыдущей части. Вот, как это выглядит в обратную сторону:
Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!