Что такое десятичные логарифмы

Десятичный логарифм

Определение. Десятичный логарифм — логарифм по основанию 10.

Калькулятор десятичных логарифмов

Свойства десятичного логарифмов

lg( x · y ) = lg x + lg y

lg 100 = lg 10 2 = 2

lg 1000 = lg 10 3 = 3

Запишем очевидное равенство:

lg b · lg a = lg a · lg ab

Возведем 10 в соответствующие степени

10 lg b · lg a = 10 lg a · lg b

(10 lg b ) lg a = (10 lg a ) lg b

Используем формулы логарифма произведения и степени получим:

lg 6 = lg (2·3)= lg 2 + lg 3 = a + b ;

lg 30 = lg (5·2·3)= lg 5 + lg 2 + lg 3 = a + b + c ;

Вычислить log₉ 5 · log₂₅ 27.

Перейдем к основе 10:

log₉ 5 · log₂₅ 27 = lg 5 lg 9 · lg 27 lg 25

Используем свойство логарифма степени lg x n = n lg x :

lg 5 lg 9 · lg 27 lg 25 = lg 5 lg 3 2 · lg 3 3 lg 5 2 = lg 5 2 lg 3 · 3 lg 3 2 lg 5 = 3 4

Перейдем к основе 10:

log ₃₀ 8 = lg 8 lg 30 = lg 2 3 lg (3 · 10) =

Используем свойство логарифма степени, произведения, частного и то что 2= 10 5 :

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Источник

Логарифм. Десятичный логарифм.

За основание логарифмов нередко берут цифру десять. Логарифмы чисел по основанию десять именуют десятичными. При проведении вычислений с десятичным логарифмом общепринято оперировать знаком lg, а не log; при этом число десять, определяющие основание, не указывают. Так, заменяем log₁₀105 на упрощенное lg105; а log₁₀2 на lg2.

Для десятичных логарифмов типичны те же особенности, которые есть у логарифмов при основании, большем единицы. А именно, десятичные логарифмы характеризуются исключительно для положительных чисел. Десятичные логарифмы чисел, больших единицы, положительны, а чисел, меньших единицы, отрицательны; из двух не отрицательных чисел большему эквивалентен и больший десятичный логарифм и т. д. Дополнительно, десятичные логарифмы имеют отличительные черты и своеобразные признаки, которыми и поясняется, зачем в качестве основания логарифмов комфортно предпочитать именно цифру десять.

Перед тем как разобрать эти свойства, ознакомимся с нижеследующими формулировками.

Целая часть десятичного логарифма числа а именуется характеристикой, а дробная — мантиссой этого логарифма.

Характеристика десятичного логарифма числа а указывается как [lg а], а мантисса как а>.

Возьмем, скажем, lg 2 ≈ 0,3010.Соответственно[lg 2] = 0, ≈ 0,3010.

Подобно и для lg 543,1 ≈2,7349. Соответственно,[lg 543,1] = 2, ≈ 0,7349.

Достаточно повсеместно употребляется вычисление десятичных логарифмов положительных чисел по таблицам.

Характерные признаки десятичных логарифмов.

Первый признак десятичного логарифма. Десятичный логарифм целого не отрицательного числа, представленного единицей со следующими нулями, есть целое положительное число, равное численности нулей в записи выбранного числа.

Возьмем, lg 100 = 2, lg 1 00000 = 5.

То а= 10 n , из чего получаем

,

То a= 10 -n и получается

Третий признак. Характеристика десятичного логарифма не отрицательного числа, большего единицы, равна численности цифр в целой части этого числа исключая одну.

Разберем данный признак 1) Характеристика логарифма lg 75,631 приравнена к 1.

Из чего делаем обобщение

Действительно, по формуле логарифма произведения

lg (739,15 •100) = lg 739,15 + 2;

lg (28 •10000) = lg 28 + 4.

Перемещение запятой в положительной десятичной дроби на п знаков вправо равноценно операции перемножения заданной дроби с 10 n . Следовательно, при перемещении запятой в положительной десятичной дроби на п знаков вправо десятичный логарифм возрастет на п.

При перемещении запятой в положительной десятичной дроби на п знаков влево десятичный логарифм уменьшается на п.

Все обоснованные ранее признаки десятичных логарифмов касались их характеристики. Далее разберем признаки мантиссы десятичных логарифмов.

Седьмой признак десятичного логарифма. Мантисса десятичного логарифма положительного числа не меняется, если умножить это число на 10 n с заданным целым показателем п.

Обоснованно, что при заданном целом п (как положительном, так и отрицательном)

Но дробная часть числа не меняется при прибавлении к нему целого числа.

Смещение запятой в десятичной дроби вправо или влево равнозначно операции перемножения этой дроби на степень числа десять с целым показателем п (положительным или отрицательным). И следовательно, при смещении запятой в положительной десятичной дроби влево или вправо мантисса десятичного логарифма этой дроби не меняется.

Источник

Десятичные и натуральные логарифмы

п.1. Десятичный логарифм и его свойства

Основание десятичных логарифмов \(10\gt 1\), поэтому они обладают всеми свойствами логарифмов с основанием больше единицы (см. §30 данного справочника).

Но у десятичных логарифмов есть также целых ряд дополнительных свойств, благодаря которым в докомпьютерную эпоху они широко использовались для трудоемких вычислений. Роль калькулятора тогда выполняли логарифмическая таблица и логарифмическая линейка.

Если использовать унифицированную запись, как в представленной таблице, то мантисса всегда лежит в промежутке \(0\lt \lg a\lt 1\). У чисел, отличающихся только порядком, мантисса одинакова. Можно составить таблицы мантисс и пользоваться ими для умножения и деления, «разбавляя» их несложным сложением и вычитанием целых характеристик по необходимости.

Первые таблицы логарифмов были изданы в 1617 году оксфордским математиком Бригсом. Таблицы пересчитывались, дополнялись и переиздавались вплоть до 70-х гг. ХХ века, когда на столах стали появляться калькуляторы.
Таблицы Брадиса, которыми по традиции пользуются наши школьники с 1921 года, издаются до сих пор и постепенно перекочевывают в Интернет.

Непосредственная связь десятичных логарифмов с десятичной системой исчисления делает их удобным инструментом для оценки порядка числа и сравнения чисел.

В практике приближенных вычислений используется следующая оценочная таблица:

Относительная погрешность этих приближений (кроме \(\lg 3)\) \(\delta\sim 0,5\text<%>\)

Например:
Сравним \(\log_23\) и \(log_5⁡8\)
Сравнивая с помощью оценки, получаем: \begin \log_23=\frac<\lg 3><\lg 2>\approx\frac<0,5><0,3>=\frac53,\ \ \log_58=\frac<\lg 8><\lg 5>\approx\frac<0,9><0,7>=\frac97\\ \frac<35><21>\gt \frac<27><21>\Rightarrow \frac53\gt \frac97\Rightarrow\log_23\gt\log_58 \end

п.2. Натуральный логарифм и его свойства

Основание натуральных логарифмов e>1, поэтому они обладают всеми свойствами логарифмов с основанием больше единицы (см. §30 данного справочника).

Для приближенного вычисления значения натурального логарифма используется «ряд Меркатора»:

Например:
С точностью до первого слагаемого: \(\ln 1,3=\ln(1+0,3)\approx 0,3\)
До второго слагаемого: \(\ln 0,3\approx 0,3-\frac<0,3^2><2>=0,255\)
До третьего слагаемого: \(\ln 0,3\approx 0,3-\frac<0,3^2><2>+\frac<0,3^3><3>=0,264\) и т.д.

Натуральные логарифмы настолько распространены в различных областях научных исследований, что когда вообще речь заходит «логарифмах», по умолчанию подразумевают именно их. Если же у вас в работе какие-то другие «логарифмы» (по основанию 2 или 10, например), это нужно уточнять.

п.3. Примеры

Пример 1. Найдите \(x\):
a) \( \lg x=2\lg a+\lg 7 \)
\(\lg x=\lg a^2+\lg 7=\lg(7a^2)\)
\(x=7a^2\)

Пример 2. Прологарифмируйте по основанию 10:
a) \(x=\frac<3a^2\sqrt[3]>\) \begin \lg x=\lg\frac<3a^2\sqrt[3]>=\lg 3+\lg a^2+\lg\sqrt[3]-\lg c^5-\lg(a-b)=\\ =\lg 3+2\lg a+\frac73\lg b-5\lg c-\lg(a-b) \end

Расчет относительной погрешности приближения на границах окрестностей \(|x|\lt 0,1\) и \(|x|\lt 0,2\) представлен в таблице:

Источник

Что такое логарифм. Как посчитать логарифм. Свойства логарифмов. Примеры решения логарифмов

Многие школьники считают логарифмы сложной темой в курсе математики. Но если разобрать, что такое логарифм подробно, от простого к сложному, то на ЕГЭ вы не станете их опасаться.

Часто у учеников возникает путаница, где аргумент, а где основание логарифма. И что же нужно возвести в степень, чтобы этот логарифм, наконец, посчитать.

В этой статье мы откроем секрет, как легче запомнить принцип решения логарифма.

Итак, давайте разбираться, что такое логарифм.

Что такое логарифм и как его посчитать

Логарифм имеет следующий вид:

где a – это основание логарифма,

b – это аргумент логарифма

Чтобы узнать значение логарифма приравняем его к X.и преобразовываем вЗапомните, что именно основание (оно выделено красным) возводится в степень.

Чтобы было легче, можно запоминать так – основание всегда остается внизу (и в первом, и во втором выражении a внизу)!

Чтобы вычислить данный логарифм, необходимо приравнять его к X и воспользоваться правилом, описанным выше:А в какую степень нужно возвести 2, чтобы получилось 8? Конечно же в третью степень, таким образом:

Еще раз обращаю ваше внимание, что основание (в нашем случае это – 2) всегда находится внизу и именно оно возводится в степень.

Логарифмы со специальным обозначением

Для некоторых логарифмов в математике введены специальные обозначения. Это связано с тем, что такие логарифмы встречаются особенно часто. К таким логарифмам относятся десятичный логарифм и натуральный логарифм. Для этих логарифмов справедливы все правила, что и для обычных логарифмов.

Десятичный логарифм

Десятичный логарифм обозначается lg и имеет основание 10, т.е.

Чтобы вычислить десятичный логарифм, нужно 10 возвести в степень X.

Например, вычислим lg100

Натуральный логарифм

Натуральный логарифм обозначается ln и имеет основание e, то есть

Чтобы вычислить данный логарифм нужно число е возвести в степень x. Некоторые из вас спросят, что это за число такое е? Число е – это иррациональное число, т.е. точное его значение вычислить невозможно. е = 2,718281…

Сейчас не будем подробно разбирать, зачем это число нужно, просто запомним, что

И вычислить его можно таким образом:

Основные свойства логарифмов

Логарифмы можно преобразовывать, но для этого необходимо знать правила, которые называются основными свойствами логарифмов. Данные свойства обязательно нужно знать каждому ученику! Без знания этих свойств невозможно решить ни одну серьезную логарифмическую задачу. Вот эти свойства:

Совет – тренируйтесь применять эти свойства в обе стороны, то есть как слева направо, так и справа налево!

Рассмотрим свойства логарифмов на примерах.

Логарифмический ноль и логарифмическая единица

Это следствия из определения логарифма. И их нужно обязательно запомнить. Эти простейшие свойства нередко вводят учеников в ступор.

Запомните, что логарифм от a по основанию а всегда равен единице:

log_a a = 1 – это логарифмическая единица.

Если же в аргументе стоит единица, то такой логарифм всегда равен нулю независимо от основания, так как a 0 = 1:

log_a 1 = 0 – логарифмический ноль.

Основное логарифмическое тождество

В первой формуле число m становится степенью, которая стоит в аргументе. Данное число может быть любым. Некоторые выражения могут быть решены только с помощью этого тождества.

Вторая формула по сути является просто переформулированным определением логарифма

Разберем применение тождества на примере:

Необходимо найти значение выраженияСначала преобразуем логарифм

Вернемся к исходному выражению и применим правило умножения степеней с одинаковым основанием:Теперь применим основное логарифмическое тождество и получим:

Сумма логарифмов. Разница логарифмов

Логарифмы с одинаковыми основаниями можно складывать:Логарифмы с одинаковыми основаниями можно вычитать:Мы видим, что исходные выражения состояли из логарифмов, которые по отдельности не вычисляются, а при применении свойств логарифмов у нас получились нормальные числа. Поэтому повторим, что основные свойства логарифмов нужно знать обязательно!

Обратите внимание, что формулы суммы и разности логарифмов верны только для логарифмов с одинаковыми основаниями! Если основания разные, то данные свойства применять нельзя!

Вынесение показателя степени из логарифма

Вынесение показателя степени из логарифма:

Переход к новому основанию

Когда мы разбирали формулы суммы и разности логарифмов, то обращали внимание на то, что основания логарифмов должны быть при этом одинаковыми. А что же делать, если основания логарифмов разные? Воспользоваться свойством перехода к новому основанию.

Такие формулы чаще всего нужны при решении логарифмических уравнений и неравенств.

Разберем на примере.

Необходимо найти значение такого выраженияДля начала преобразуем каждый логарифм с помощью свойства вынесения показателя степени из логарифма:

Теперь применим переход к новому основанию для второго логарифма:Подставим полученные результаты в исходное выражение:

10 примеров логарифмов с решением

1. Найти значение выражения2. Найти значение выражения3. Найти значение выражения4. Найти значение выражения5. Найти значение выражения6. Найти значение выраженияСначала найдем значениеДля этого приравняем его к Х:Тогда изначальное выражение принимает вид:

7. Найти значение выраженияПреобразуем наше выражение:Теперь воспользуемся свойством вынесения показателя степени из логарифма и получим: 8. Найти значение выраженияТак как основания логарифмов одинаковые, воспользуемся свойством разности логарифмов:9. Найти значение выраженияТак как основания логарифмов разные, применять свойство суммы логарифмов нельзя. Поэтому решаем каждый логарифм по отдельности:Подставляем полученные значения в исходное выражение:

10. Найти значение выраженияОбращаем внимание, что данное выражение – это не произведение логарифмов. У логарифма по основанию 4 подлогарифным выражением является log₂16. Поэтому сначала найдем значение log₂16, а затем подставим полученный результат в log₄:

Надеюсь, теперь вы разобрались, что такое логарифм.

Источник

Понятия и термины

Впервые упоминание о логарифмах встречается в XIX веке в астрономических вычислениях. Сам же термин ввёл в обиход математик Спейдел. В 1893 году обозначать натуральный логарифм буквами ln предложил немецкий учёный Прингсхейм. Но лишь только в книге «Введение в анализ бесконечности» Эйлер дал определения логарифмам и описал их свойства, выделив при этом выражение с основанием равным десяти.

Существует несколько определений логарифмов. Для того чтобы разобраться в сущности термина нужно представить себе любое простое уравнение, содержащее степень. Например, 3 x = 9. Это выражение называется показательным, так как неизвестное число стоит в показателе степени. Равенство будет верным при иксе равному два. Ведь три в квадрате это девять.

Теперь можно рассмотреть другое уравнение: 3 x = 7. Если попробовать его решить, то можно обнаружить, что подобрать неизвестное значение будет довольно сложно. Интуитивно можно понять, что ответ будет располагаться между числом три в степени один и три в степени два. Искомое число и было решено назвать логарифмом. Записывается он как x = log3 7. Читается же формула как икс равный логарифму семи по основанию три.

Цифра, стоящая в нижнем регистре записи, называется основанием, а в верхней части аргументом. То есть любое выражение вида c x = k можно записать как x = logc k. Эта запись очень удобна для обозначения иррациональных чисел.

Логарифм можно записать только при выполнении условия: logp K = b, где pb = k, p > 0, k > 0, p ≠ 0. Существует три вида логарифма:

Десятичный логарифм записывают упрощённой записью: log10. Например, число два можно представить, как lg 100. Эта запись верна, так как используя определение, запись можно переписать в виде: 10 2 = 100. Для того чтобы научиться решать задачи по нахождению логарифмов нужно знать их свойства, формулы сокращённого умножения и правила вычисления степеней.

Свойства и формулы

Формулы сокращённого умножения изучают в средней школе на уроках алгебры. Учащимся предлагается выучить семь основных выражений, собранных в таблицу. С их помощью можно быстро и в уме рассчитывать квадраты даже больших чисел, что используется при нахождении логарифмов. Доказываются они просто раскрытием скобок. Из основных равенств умножения можно выделить следующие:

На этих формулах основаны свойства десятичных логарифмов. Большинство задач можно решить, зная только эти закономерности. Первое свойство вытекает из самого определения выражения: log​p ​​p v ​ ​= v. Для доказательства этого свойства можно использовать рассуждение, что если log​і ​​p​ ​= v, то i v = p. Тогда отношение logk p / logk I будет равняться: logk i v / logk I = v * logk i / logk I = v = log​і ​​p​. Что и требовалось доказать.

Второе и третье свойство помогает определить сумму логарифмов и посчитать их разницу. Согласно ему сумма выражений с одинаковым основанием равняется их произведению: logp i + logp c = logp (i * c). А также используется то что разность произведений с одинаковыми основаниями тождественна логарифму отношения: logp i − logp c = logp c * i.

Четвёртое свойство позволяет при необходимости степень выносить за знак логарифма: logk i v ​ ​ = n * logk i. Пятое правило гласит, что если в основании логарифма стоит степень, то её можно переместить за знак функции: log​k n ​​​i = ​ 1/ n​​​ ​ * log​k ​​i. В отличие от четвёртого свойства показатель степени всегда выносится как обратное число.

Следующее свойство сообщает, что если основание и аргумент имеют степень, то эти показатели можно вынести за знак выражения как дробь: log​k​ n * ​​​​i​ m ​​ =​ (m​/n) ​ * log​k​​i. При этом если степени совпадают по своему значению, это правило можно записать как log k n i n = log k i. Седьмое свойство помогает решать логарифмы с разным основанием. Так, любой логарифм можно записать в виде равенства: log k i = log c i / log c k.

Эти свойства применимы к любым видам логарифмов. При этом существует ещё одно позволяющее поменять местами основание и аргумент. Для этого нужно просто единицу разделить на логарифм: log k​ b = 1 / ​ log k b.

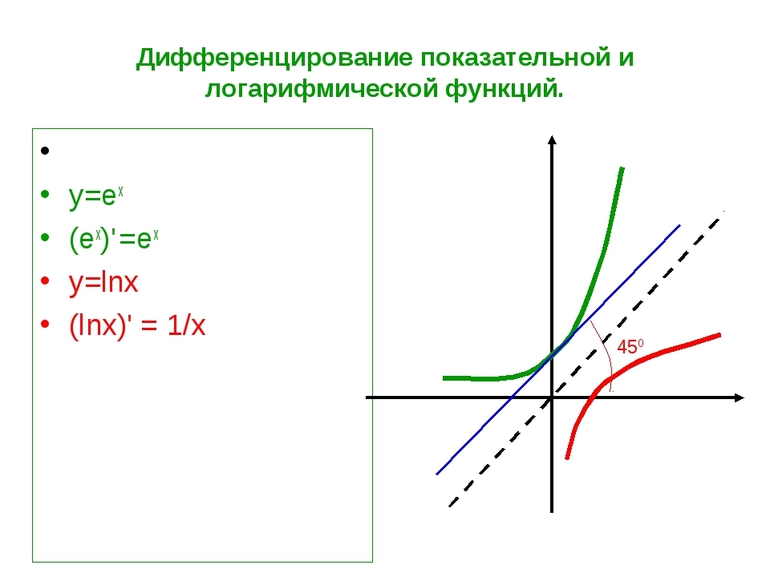
Дифференцирование и функция

Производная десятичного логарифма определяется, как отношение в числителе которого стоит единица, а в знаменателе показатель. Для доказательства этого можно рассмотреть произвольное число, которое больше единицы. Пусть имеется следующая функция: t = logc p.

Воспользовавшись свойством формулу можно упростить и записать: t’ = 1/t * logc p = (1/t) * (1/ln p) = 1 / t * ln p. То есть получить рассматриваемую функцию. Тождественным доказательством будет и метод вынесения постоянной за знак дифференцирования: (logc p)’ = (ln p / ln c)’ = ((1 / ln c ) * ln p )’ = (1/ ln c) * (1/ p) = 1 / p ln c.

Интеграл функции можно записать выражением: ∫ ln x dx = x * ln x – x + C. Находят его способом интегрирования по частям. Этим методом выражение сводится к более простому виду.

Функцию десятичного логарифма можно записать как y = lg x. График имеет вид плавной возрастающей кривой, которую ещё называют логарифмикой. К основным характеристикам функции относят:

Функция монотонная, то есть всё время она не убывает и не возрастает. Иными словами, она всегда неотрицательная или неположительная, но при этом всюду дифференцируемая. Производная для выражения находится с помощью формулы: (d/dx) lg x = lg e / x. Ось ординат обладает свойством вертикальной асимптотности, так как при лимите стремящимся к нулю логарифм по иксу будет равный минус бесконечность.

Примеры решения задач

При решении тождеств, содержащих тригонометрические функции, поможет и сборник таблиц Брадиса. Это пособие, в котором собраны ответы для чаще всего встречающихся типовых выражений.

Следующие типы примеров наиболее часто предлагаются в школе для самостоятельного решения:

Но бывает так, что самостоятельно решить задачу довольно сложно из-за громоздкости записи уравнения. При этом не так сложно провести вычисления, как правильно выбрать алгоритм решения. Поэтому в таких случаях используют так называемые онлайн-калькуляторы.

Использование онлайн-калькулятора

Использовать сервисы предлагающие услуги по вычислению десятичного логарифма, довольно удобно. Всё, что требуется от пользователя, — это интернет-канал и браузер с поддержкой флеш-технологии. Доступ к онлайн-калькуляторам предоставляется бесплатно, при этом даже нет необходимости в регистрации или указании каких-либо данных.

Онлайн-расчётчики позволяют не только получить быстрый и правильный ответ вычисления выражения любой сложности, но и предоставляют подробное решение с пояснениями. Кроме того, на страницах таких сервисов содержится краткая теория с примерами. Так что проблем с понятием, откуда взялся ответ возникнуть не должно.

Программы, используемые для расчётов, написаны на Java и включают в свой алгоритм все необходимые формулы. Пользователь, загрузив сервис должен ввести условие задачи в специально предложенную формулу и нажать кнопку «Решение» или «Вычислить». После чего буквально через две три секунды появится ответ с поэтапным решением.

Такие сервисы будут полезны не только учащимся для проверки своих знаний, но и даже инженерам, проводящим сложные вычисления. Ведь самостоятельный расчёт требует повышенного внимания и скрупулёзности. При этом любая незначительная ошибка приведёт к неправильному ответу. В то же время появление ошибки при вычислении на онлайн-калькуляторе практически невозможно.

По мнению пользователей, из нескольких десятков существующих сайтов можно выделить тройку лидеров:

Приведённые онлайн-калькуляторы для десятичного логарифма имеют интуитивно понятный интерфейс. Используемые программы написаны российскими программистами и не содержат рекламного и вредоносного кода. Решив несколько задач с помощью этих порталов, пользователь научится самостоятельно вычислять любые логарифмические уравнения. То есть калькуляторы смогут не только подтянуть знания на нужный уровень, но и даже заменить репетитора по математике.

Источник