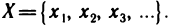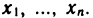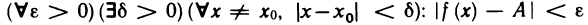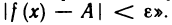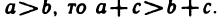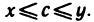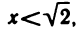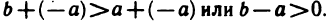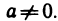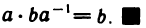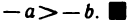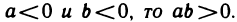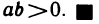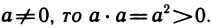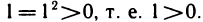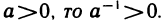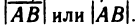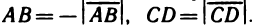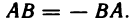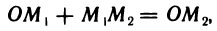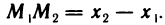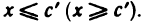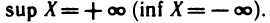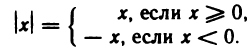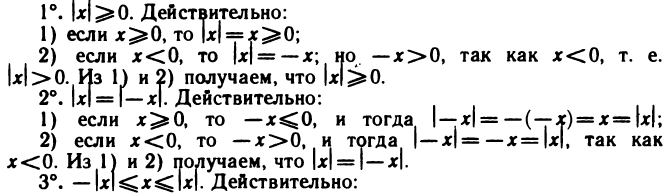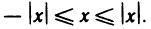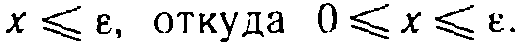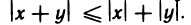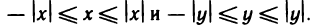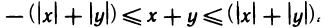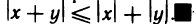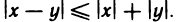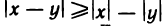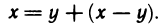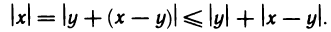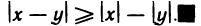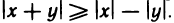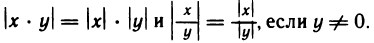Что такое действительные числа в математике определение

Действительные числа, определение, примеры

Пополнение рациональных чисел

Непосредственно проверяется, что это построение корректно и полученная таким образом четвёрка является полным упорядоченным полем. В силу изоморфизма полных упорядоченных полей эту структуру можно называть полем действительных чисел и более того считать, что

Какие числа называются действительными?

__Давайте же строго научно определим, какие числа называются действительными, а также попытаемся ответить на следующие часто встречающиеся вопросы:

является ли ноль действительным числом?

что такое целая часть действительного числа?

какими свойствами обладает модуль действительного числа?

__На самом деле эти вопросы не такие уж сложные, как может показаться на первый взгляд. Для начала определимся с самим понятием действительного числа.

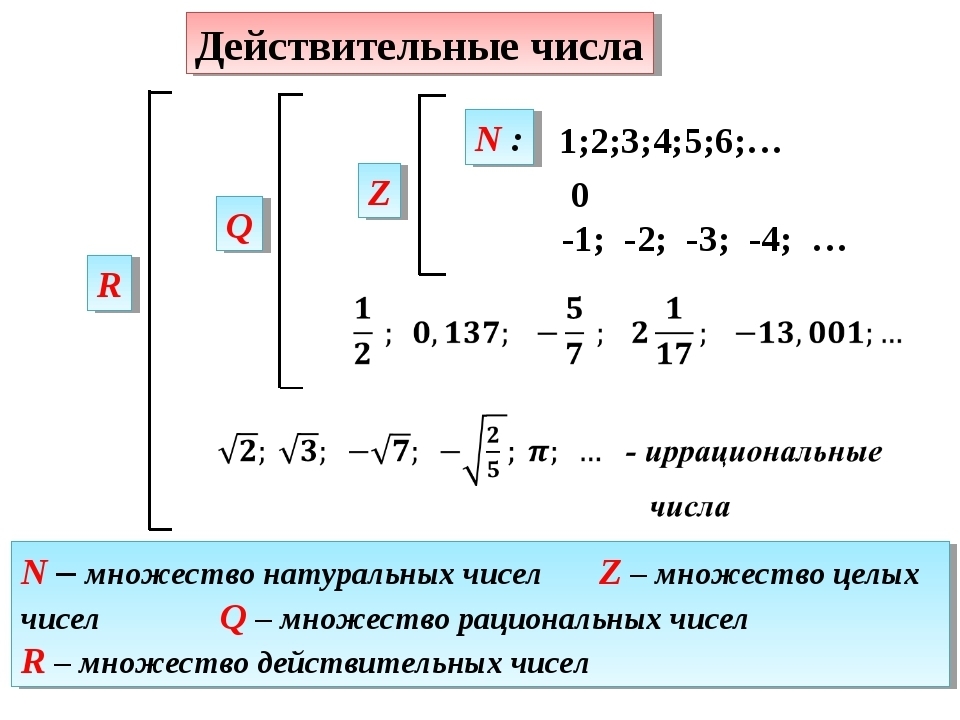
Определение действительного числа

Определение1: Действительное число (также его часто называют вещественным ) — это любое положительное число, отрицательное число или нуль.

Определение2: Множеством действительных чисел называют объединение множеств рациональных и иррациональных чисел.

Строго Научное Определение:

Положительным действительным (вещественным) числом «α» называют бесконечную десятичную дробь N, n₁ n₂… n_k,… не оканчивающуюся последовательностью девяток.

__Добавив к отрицательным и положительным действительным числам число 0 получим полное множество действительных чисел

Обратите внимание на нюанс, указанный в Строго Научном Определении. Все дело в том, что любую конечную десятичную дробь N, n1 n2… nk можно записать в виде бесконечной десятичной дроби N, n1 n2… nk 000…0… оканчивающейся «хвостом» из нулей

При этом дроби 1,1 соответствует последовательность пар десятичных приближений :

Рассмотрим теперь бесконечную десятичную дробь 1,09999…. Для неё последовательность пар десятичных приближений имеет вид (1,09; 1,10), (1,099; 1,100) и т. д.

В этом случае совпадают все десятичные приближения по избытку: 1,10=1,100=…

__Обратите внимание, приближения по недостатку для первой дроби совпадают с приближениями по избытку для дроби второй. Таким образом обе дроби геометрически выражают одну и ту же длину

Именно поэтому, (для того чтобы не обозначать одно и то же число двумя способами ) условились не использовать бесконечных десятичных дробей, оканчивающихся бесконечной последовательностью девяток. Такие дроби всегда можно заменить конечной десятичной дробью, поставив вместо девяток нули и увеличив на 1 цифру, стоящую перед ними. Например :

Еще один нюанс: последовательность из девяток должна быть именно бесконечной,

Давайте подведем итог.

Действительным ( иногда его называют вещественным) числом называется любое целое число, а также все конечные и бесконечные дроби.

Дроби, оканчивающиеся бесконечной последовательностью девяток для удобства использования округляют в большую сторону.

Различают положительные действительные числа, отрицательные действительные числа и ноль.

Множество действительных чисел разделяется на множества рациональных и иррациональных чисел.

__Надеюсь вы разобрались с понятием действительного числа и со всеми теми особенностями, которые присущи таким числам. Если же вам по прежнему что-то непонятно — добро пожаловать в Вопрос-Ответник.

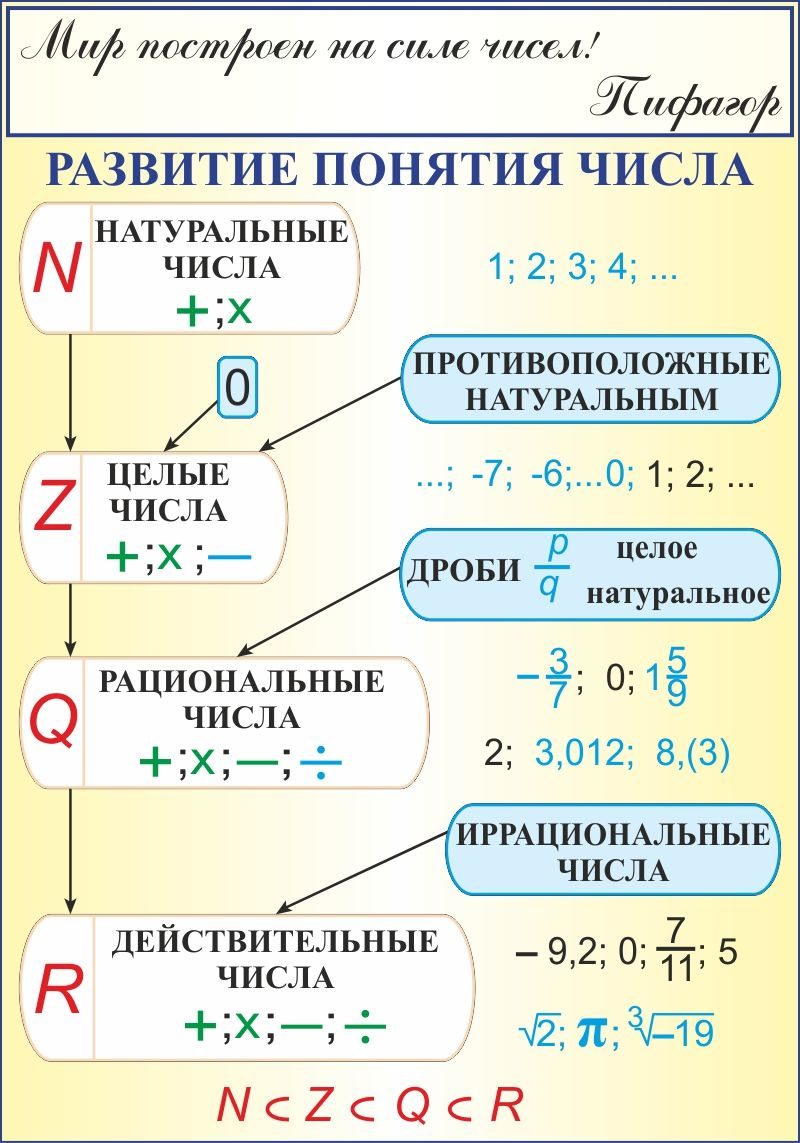
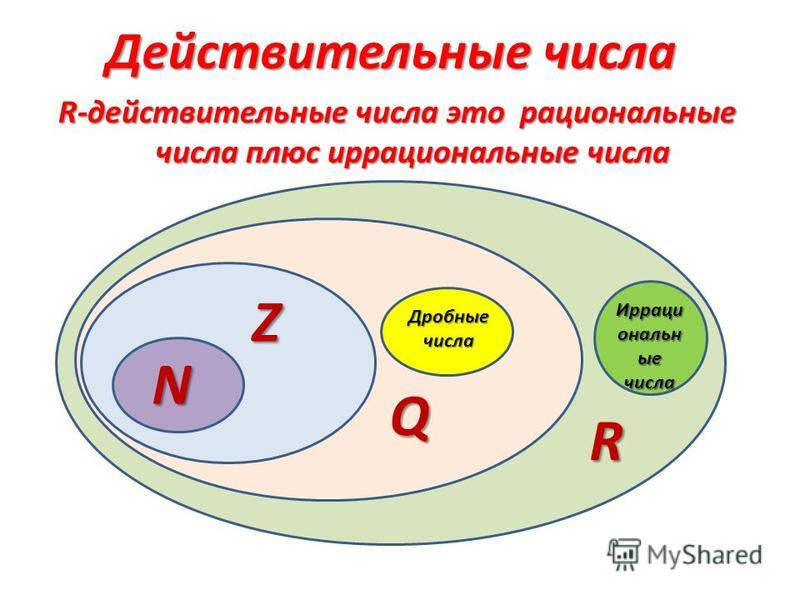
Множества чисел

Зачем вообще нужно определение разных множеств чисел? Ведь было бы куда проще просто взять число и начать выполнять какие-либо действия. Но все не так просто.

Вы наверняка уже сталкивались со сложностью вычисления дробей? Сложение, умножение, деление и вычитания – все действия с дробями отличаются от действий с привычными нам натуральными числами, ведь они относятся другому подмножеству.

То же касается, к примеру, отрицательных чисел. Складывать их с положительными можно, но только по отдельным правилам. Поэтому в вопросе множеств чисел нужно разбираться с самого начала.

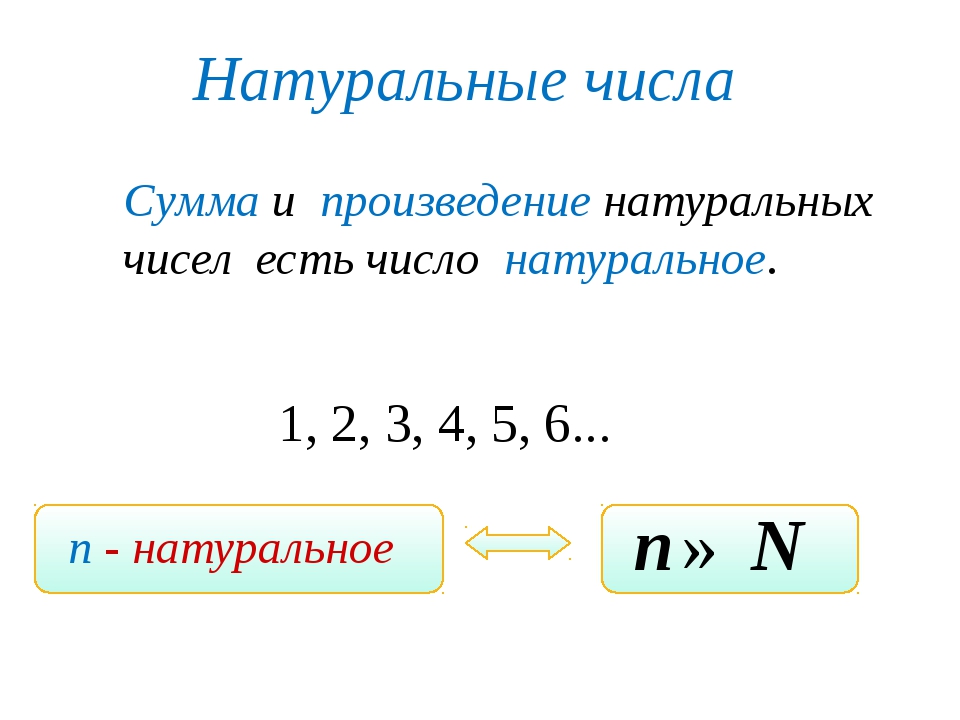
Действительным числами зовутся любые:

Иррациональные числа так же входят в сообщество действительных чисел.

[править] Обобщения

В алгебре и анализе вводятся комплексные числа — числа, представляющих собой сумму вещественного и мнимого числа (вещественное число, умноженное на абстрактную величину «корень из −1», обозначаемую буквой i). В рамках нестандартного анализа к вещественным числам добавляют бесконечно малые и бесконечно большие числа разных порядков. Рассматривается также алгебра кватернионов и др. обобщения.

Рациональные числа можно расширить не только до поля вещественных чисел, но и до поля p-адических чисел, если использовать другую метрику, связанную с делимостью на заданное простое число p (у «маленьких чисел» числитель дроби в несократимом представлении делится на «большую» степень простого числа p) и рассмотреть пополнение рациональных чисел по этой метрике. На базе p-адических чисел удается построить аналоги многих конструкций из математического анализа, созданных для вещественных чисел.

[править] Аксиоматическое определение

Вещественные числа можно определить аксиоматически. Записанные в сокращенном виде аксиомы вещественных чисел выглядят так.

Источник

Вещественные числа в математике с примерами решения и образцами выполнения

Вещественные или действительные числа — это математическая абстракция, используемая для представления и сравнения значений физических величин. Чаще всего такое число представляют как описывающее положение точки или прямой. Множество вещественных чисел обозначается буквой R, которую нередко называют вещественной прямой.

Множества и обозначения. Логические символы

Понятие множества является одним из основных в математике. Оно принадлежит к так называемым первичным, неопределяемым понятиям. Слова «совокупность», «семейство», «система», «набор» и т. п. — синонимы слова «множество». Примерами множеств могут служить множество студентов данной аудитории; совокупность тех из них, кто сдал вступительные экзамены без троек; семейство звезд Большой Медведицы; система трех уравнений с тремя неизвестными; множество всех целых чисел и т. д. Из приведенных примеров следует, что множество может содержать конечное или бесконечное число произвольных объектов.

Объекты, из которых состоит множество, называются его элементами или точками. Множества часто обозначают большими, а их элементы — малыми буквами. Если х — элемент множества X, то пишут (х принадлежит X). Если х не является элементом множества X, то пишут (х не принадлежит X). Если — некоторые элементы, то запись означает, что множество X состоит из элементов Аналогичный смысл имеет запись

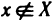
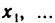
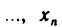
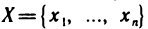
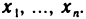
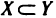
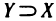
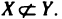
Пусть X и У — два множества. Если X и У состоят из одних и тех же элементов, то говорят, что они совпадают, и пишут X=Y. Если в X нет элементов, не принадлежащих У, то говорят что X содержится в У или что X — подмножество множества У. В этом случае пишут или (Y содержит X). Если X не содержится в У, то пишут В математике часто используется пустое множество. Оно не содержит ни одного элемента и обозначается символом Пустое множество является подмножеством любого множества.

В дальнейшем нам придется иметь дело с различными множествами вещественных чисел*. Всюду, где это не может привести к неточности, для краткости вещественные числа будем называть просто числами.

* Вместо термина «вещественные числа» часто используют термин «действительные числа».

Пусть Р (х) — какое-то свойство числа х. Тогда запись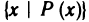
означает множество всех таких чисел, которые обладают свойством
Р(х). Например, множество 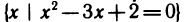есть совокупность
корней уравнения 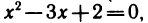т. е. это множество состоит из
двух элементов: 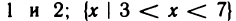— множество всех чисел, удовлетворяющих неравенствам т. е. это пустое множество.

Если — произвольные числа, то запись означает, что число х максимальное (минимальное) из чисел

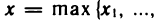
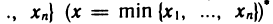
В математических предложениях (формулировках определений, теорем и т. д.) часто повторяются отдельные слова и целые выражения. Поэтому при их записи полезно использовать экономную логическую символику.

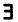
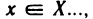
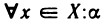
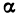
Здесь мы укажем лишь несколько самых простых и употребительных логических символов. Вместо слова «существует» или «найдется» используют символ [перевернутую латинскую букву Е (от английского слова Existence — существование)], а вместо слов «любой», «каждый», «всякий» — символ [перевернутое латинское А (от английского слова Any — любой)]. Например, запись означает: «существует число х из множества X, такое, что …». Запись означает: «для любого числа х из множества X», а запись означает: «для любого числа х из множества X выполняется (или имеет место) утверждение ».

Для облегчения понимания и чтения утверждений, записанных с помощью логических символов, все, что относится только к каж- каждому из них, заключают в круглые скобки. Так, например, запись
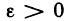
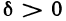
читается так: «для любого существует такое, что для
всех х, не равных хо и удовлетворяющих неравенству 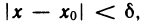выполняется неравенство

Символ в тексте означает конец доказательства.

Вещественные числа и их основные свойства

В курсе элементарной математики дается некоторое представление о вещественных числах. Из этого курса известно, что множество
вещественных чисел состоит из рациональных и иррациональных
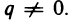
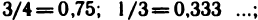
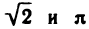
чисел. Рациональным называется число, которое можно представить в виде p/q, где р и q — целые числа, причем Иррациональным называется всякое вещественное число, которое не является рациональным. Всякое рациональное число является либо целым, либо представляется конечной или периодической бесконечной десятичной дробью. Иррациональное же число представляется непериодической бесконечной десятичной дробью. Например, рациональные числа 3/4 и 1/3 можно представить в виде следующих десятичных дробей: иррациональные числа — в виде непериодических бесконечных десятичных дробей:

Систематизируем сведения о вещественных числах, перечислим основные свойства вещественных чисел, а затем выведем из них некоторые следствия.

Сложение и умножение вещественных чисел

Для любой пары а и b вещественных чисел определены и притом единственным образом два вещественных числа 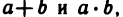называемые соответственно их суммой и произведением, причем имеют место следующие свойства. Каковы бы ни были числа а, b и с:
1°. 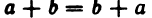(переместительное свойство).
2°. 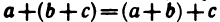(сочетательное свойство).
3°. 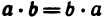(переместительное свойство).
4°. 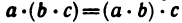(сочетательное свойство).
5°. 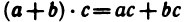(распределительное свойство).
6°. Существует единственное число 0 такое, что а + 0=а для любого числа а.
7°. Для любого числа а существует такое число (—а), что а+(-а) = 0.
8°. Существует единственное число 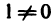такое, что для любого числа а имеет место равенство а • 1 = а.
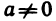
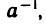
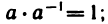
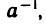
9°. Для любого числа существует такое число что число обозначают также символом

Сравнение вещественных чисел

Для любых двух вещественных чисел а и b установлено одно из отношений: а=b (а равно b), а>b (а больше b) или b>а. Отношение = обладает свойством: если а=b и b=с, то а=с.

Отношение > обладает следующими свойствами. Каковы бы ни были числа а, b и с:
10°. Если
11°. Если
12°. Если

Непрерывность вещественных чисел

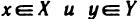
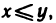
13°. Пусть X и Y — два множества, состоящие из вещественных чисел. Тогда, если для любых чисел выполняется неравенство то существует хотя бы одно число с такое, что для всех таких х и у выполняются неравенства

Отметим, что свойством непрерывности обладает множество всех
вещественных чисел, но не обладает множество только рациональных чисел. Действительно, пусть множество X состоит из рациональных чисел х, для которых выполняется неравенство
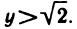
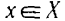
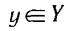
а множество У состоит из рациональных чисел у, для которых выполняется неравенство Тогда, очевидно, для любого
и любого выполняется неравенство однако
не существует рационального числа с такого, чтобы для всех таких
х и у выполнялись неравенства 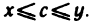В самом деле, таким чис-
числом могло бы быть только 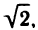но оно, как известно, не является
рациональным.

Из свойств I, II, III вытекают все остальные свойства вещественных чисел. Познакомимся лишь с некоторыми из них, но в дальнейшем будем использовать и другие, не проводя их формального доказательства.

Каковы бы ни были числа а, b, с и d:
14°. Число 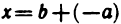является решением уравнения а+х=b.
Действительно, согласно свойствам 1°, 2°, 6°, 7° имеем: а+b+(-a)=b.

Число b+(-a) называется разностью чисел b и а и обозначается b — а. Отметим, что если а а), то
разность b — а>0. В самом деле, из неравенства b>а в силу 11°
получаем:

15°. Число 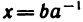является решением уравнения ах = b, если

Действительно, согласно свойствам 3°, 4°, 8°, 9° имеем:

В самом деле, так как а 0. Следовательно, на
основании свойства 11° b-а+(-b)>0 + (-b), откуда полу-
получаем:

17°. Если а>b и с>d, то a+c>b+d.
В самом деле, если а>b и c>d, то в силу свойства 11° а+c>b+c и c+b>d+b. Поэтому согласно свойству 10° а+с>b+d.

24°. Если
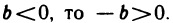
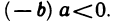
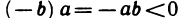
В самом деле, так как Поэтому в силу свойства 23° Следовательно, и, значит,

25°. Если
Справедливость данного утверждения следует из свойств 12° и 24°. В частности,

26°. Если
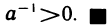
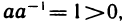
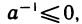
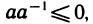
В самом деле, согласно свойствам 9° и 25° а если предположить, что то в силу свойств 20° и 23° имеем: т. е. получено противоречие. Следовательно,

Итак, мы видим, что из основных свойств I—III вещественных чисел вытекают остальные их свойства. Поэтому можно сказать, что вещественные числа представляют собой множество элементов, обладающих свойствами I—III. Такое определение вещественных чисел называется аксиоматическим, а свойства I—III — аксиомами вещественных чисел.

В заключение отметим, что, исходя из свойств I—III, любое вещественное число можно представить в виде бесконечной десятичной дроби. Однако останавливаться на рассмотрении этого вопроса не будем.

Геометрическое изображение вещественных чисел

Изображение вещественных чисел точками на координатной прямой

Введем ряд предварительных понятий. Рассмотрим произвольную прямую. На ней можно указать два взаимно противоположных направления. Выберем одно из них и на рисунке будем обозначать его стрелкой (рис. 1). Пусть, кроме того, выбрана масштабная единица для измерения длин отрезков. Прямая с выбранным на ней направлением называется осью.

Рассмотрим на оси две произвольные точки Л и В. Отрезок с граничными точками Л и В будем называть направленным, если указано, какая из точек Л и В считается началом, а какая — кон-
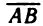
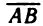
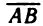
концом отрезка. Направленный отрезок с началом в точке А и концом в точке В обозначим и будем считать, что он направлен от начала к концу. Отметим, что в записи буква, обозначающая начало направленного отрезка, пишется первой, а буква, обозначающая его конец, — второй. Длина направленного отрезка обозначается так:

Для направленных отрезков, лежащих на оси (или параллель-
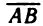
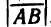
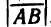
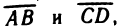
параллельных оси), вводится понятие величины направленного отрезка. Величиной АВ направленного отрезка называется число, равное , если направления отрезка и оси совпадают, и равное — , если эти направления противоположны. Для отрезков изображенных на рис. 2,

Заметим, что величины направленных отрезков 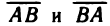при
любом направлении оси отличаются знаками:

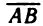
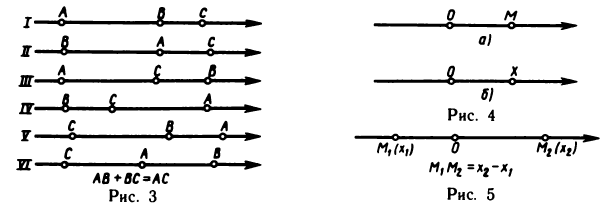
Если точки А и В совпадают, то величину направленного отрезка будем считать равной нулю.

Для любых трех точек А, В и С на оси справедливо равенство
АВ + ВС = АС,
которое назовем основным тождеством (в дальнейшем оно неоднократно используется).

Справедливость основного тождества легко устанавливается из
рисунка, но при этом нужно рассмотреть различные случаи взаимного расположения точек А, В и С на оси. Если все три точки А,
В и С различны, то таких случаев шесть (рис. 3). В каждом из этих
случаев основное тождество проверяется элементарно.

Перейдем теперь к геометрическому изображению вещественных
чисел. Рассмотрим какую-нибудь прямую. Выберем на ней направление (тогда она станет осью) и некоторую точку О (начало
координат). Прямую с выбранным направлением и началом координат назовем координатной прямой (считаем, что масштабная единица выбрана). Пусть М — произвольная точка на прямой (рис. 4, а).

Поставим в соответствие точке М число х, равное величине ОМ
направленного отрезка 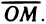Число х называется координатой
точки М. Тем самым каждой точке координатной прямой будет
соответствовать определенное вещественное число — ее координата. Справедливо и обратное: каждому вещественному числу х
соответствует некоторая точка на координатной прямой, а именно
такая точка М, координата которой равна х.

Таким образом, вещественные числа можно изображать точками
на координатной прямой. Поэтому около точки на координатной
прямой часто указывают число —ее координату (рис. 4, б).

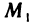
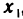
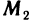
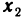
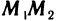
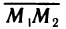
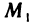
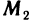
Пусть точка имеет координату , а точка — координату
(рис. 5.). Выразим величину направленного отрезка через координаты точек и . Согласно основному тождеству

откуда 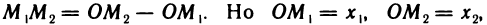поэтому

Эту формулу будем часто использовать в аналитической геометрии.

Некоторые наиболее употребительные числовые множества

Пусть а и b — два числа, причем а Грани числовых множеств

Говорят, что. множество X ограничено сверху (снизу), если существует число с такое, что для любого выполнено неравенство Число с в этом случае называется верхней (нижней) гранью множества X.

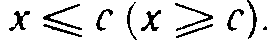
Множество, ограниченное и сверху и снизу, называется ограниченным.

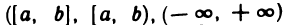
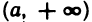
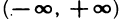
Так, например, любой конечный промежуток ограничен. Интервал есть множество, ограниченное снизу, но не ограниченное сверху; а вся числовая прямая есть множество, не ограниченное ни сверху, ни снизу.

Очевидно, что любое ограниченное сверху (снизу) множество X имеет бесконечно много верхних (нижних) граней. В самом деле, если число с является верхней (нижней) гранью множества X, то любое число с’, большее (меньшее) числа с, — также верхняя (нижняя) грань множества X, так как из справедливости неравенства 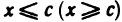следует, что

Естественно, возникает вопрос о существовании наименьшей из верхних граней ограниченного сверху множества и наибольшей из нижних граней ограниченного снизу множества.

Наименьшая из верхних граней ограниченного сверху множества X называется точной верхней гранью множества X и обозначается символом sup X, а наибольшая из нижних граней ограниченного снизу множества X называется точной нижней гранью этого множества и обозначается символом inf X*.

Примеры:

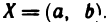
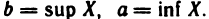
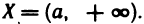
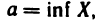
Пусть Тогда число b является точной верхней гранью множества X, а число а — его точной нижней гранью, т. е. Пусть Тогда а верхних граней и в том числе точной верхней грани данное множество не имеет.

Точная верхняя грань (sup X) обладает следующим важным свойством. Как бы мало ни было число найдется такое, что В самом деле, если бы такого числа х не нашлось, то число было бы также верхней гранью множества X и тогда число sup X не было бы точной (т. е. наименьшей) верхней гранью. Другими словами, данное свойство выражает тот факт, что число sup X является наименьшим среди чисел, ограничивающих множество X сверху, и не может быть уменьшено.

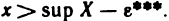
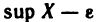
Отмеченное свойство точной верхней грани можно переформулировать следующим образом: если с = sup X, то для любого числа с’ 0, найдется такое, что (Сформулируйте данное свойство в другом виде самостоятельно.)

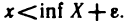
Возникает вопрос, всегда ли ограниченное сверху (снизу) множество имеет точную верхнюю (нижнюю) грань. Ответ на этот вопрос дает следующая важная теорема.

Теорема:

Любое непустое ограниченное сверху (снизу) числовое множество имеет точную верхнюю (нижнюю) грань.

Доказательство:

Пусть X — непустое множество, ограниченное сверху. Тогда множество У чисел, ограничивающих X сверху, не пусто. Из определения верхней грани следует, что для любого и любого имеет место неравенство В силу свойства непрерывности вещественных чисел существует такое число с, что для любых х и у выполняются неравенства

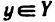
Из первого из неравенств (1) следует, что число с ограничивает множество X сверху, т..е. является верхней гранью, а из второго, — что оно наименьшее из таких чисел, т. е. является точной верхней гранью.

Случай существования точной нижней грани у не пустого ограниченного снизу множества рассматривается аналогично.

Если множество X не ограничено сверху (снизу), то условимся писать:

Абсолютная величина числа

Понятие абсолютной величины числа и неравенства, связанные с абсолютными величинами, в дальнейшем часто используются.

Определение:

Абсолютной величиной (или модулем) числа х называется само число х, если число —х, если

Абсолютная величина числа х обозначается символом |х|. Таким образом,

Из определения вытекает ряд свойств абсолютной величины числа.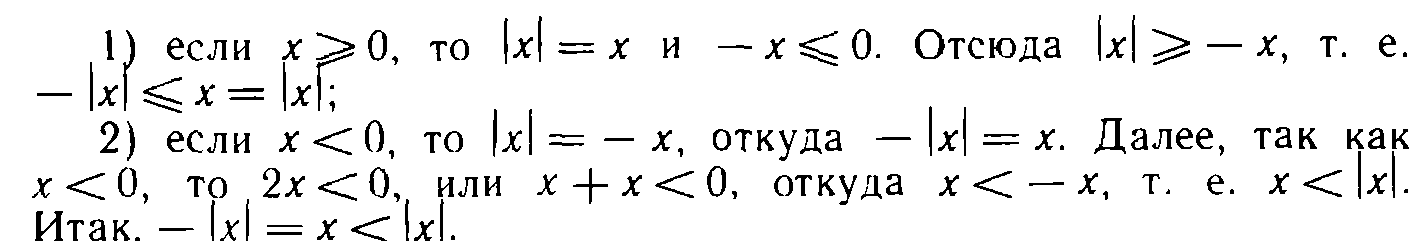Из 1) и 2) получаем, что

Поскольку следующие три свойства очень важны, докажем их в виде теорем.

Теорема:

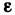
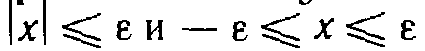
Пусть — положительное число. Тогда неравенства равносильны*
Доказательство:

Пусть Тогда:
1) если и, значит,
2) если значит, — откуда — Объединяя 1) и 2), при любом х получаем:

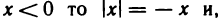
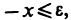
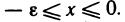
Пусть справедливы неравенства Это означает, что одновременно выполняются неравенства Из последнего неравенства имеем: Так как, по определению, |х| есть либо х, либо — х, то

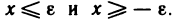
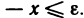
Теорема:

Абсолютная величина суммы двух чисел не больше суммы абсолютных величин этих чисел, т. е.

Доказательство:

Пусть х и у — любые числа. Согласно свойству 3° для них справедливы неравенства

Складывая их почленно, получаем

По теореме 1.2 это двойное неравенство равносильно неравенству
Заметим, что

Теорема:

Абсолютная величина разности двух чисел не меньше разности абсолютных величин этих чисел, т. е.

Доказательство:

Для любых чисел х и у имеем

По теореме 1.3 справедливо неравенство

Откуда получаем:
Заметим, что

В заключение отметим, что каковы бы ни были два числа х и у, имеют место легко проверяемые соотношения:

Свойства вещественных чисел

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник