Что такое диагональ квадрата и прямоугольника

Общая информация

В задачах по геометрии и физике приходится находить некоторые параметры прямоугольника: углы, стороны, периметр, площадь и диагонали. Все эти величины связаны между собой некоторыми соотношениями. Каждый должен уметь их рассчитывать, поскольку это необходимо не только для решения математических задач, но и в жизни. Например, при укладке керамзитной плитки на пол.

Используя свойство диагоналей, можно определить метод ее укладки. Кроме того, в физике иногда требуется рассчитать площадь поперечного сечения, а необходимая формула неизвестна. Во время планирования покупки строительных материалов нужно вычислить их количество, произведя вычисление площади или периметра помещения.

Однако формул для ведения расчетов недостаточно, поскольку нужно идентифицировать геометрическую фигуру. Для каждой из них применяются разные соотношения. В случае неверного определения вычисления окажутся недостоверными, а это негативно сказывается не только на экзаменах или контрольных, но и в финансовой сфере.

Сведения о прямоугольнике

Прямоугольником называется фигура с прямыми внутренними углами между смежными сторонами, у которой противоположные стороны равны. Его частным случаем, как говорят математики, является квадрат. У него все стороны равны, а углы также являются прямыми. Не каждый может правильно определить тип фигуры, поскольку от этого шага зависит правильность вычислений какого-либо параметра.

Для каждого геометрического тела существуют определенные критерии, по которым можно узнать его принадлежность. Эти критерии называются признаками. Некоторые новички путают признаки и свойства, но существует главное отличие, которое заключено в определении терминов «признак» и «свойство». Кроме того, специалисты предлагают простой способ, позволяющий избежать путаницы между терминами.

Идентификация или признаки

Признак — некоторые критерии, по которым можно отнести фигуру к определенному типу. Свойствами называются некоторые аксиомы и утверждения, полученные при доказательстве теорем. Идентифицировать прямоугольник можно с помощью теоремы из эвклидовой геометрии. Она имеет такую формулировку: если три угла фигуры являются прямыми, то она является прямоугольником. Для доказательства нужно выполнить такие действия:

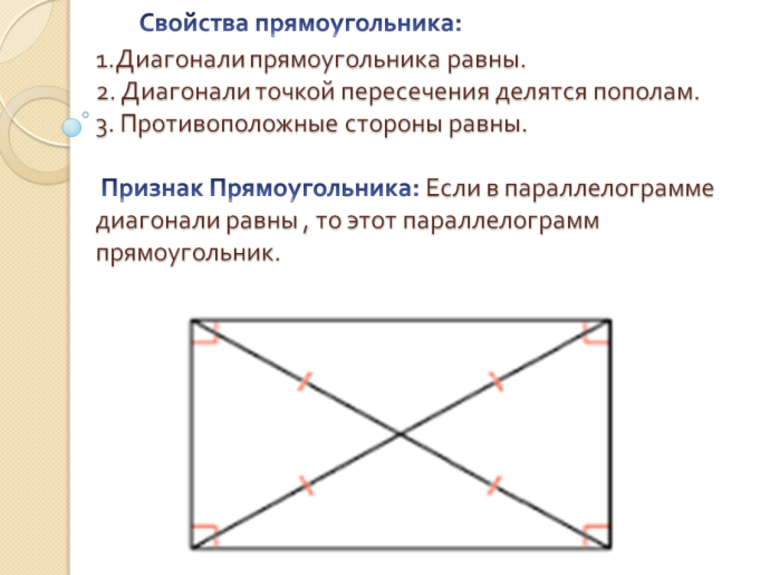
Существуют также и другие признаки, по которым можно идентифицировать фигуру. По одному из них можно определить ее принадлежность к прямоугольнику. К признакам можно отнести такие:

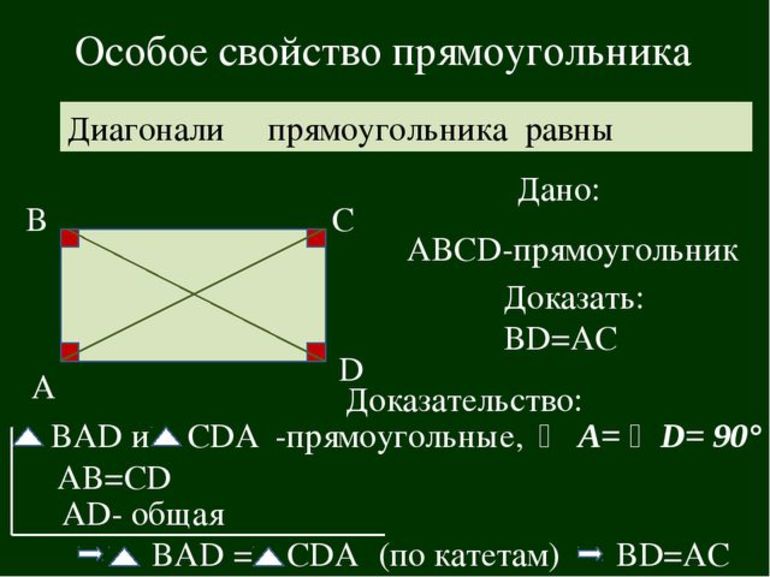
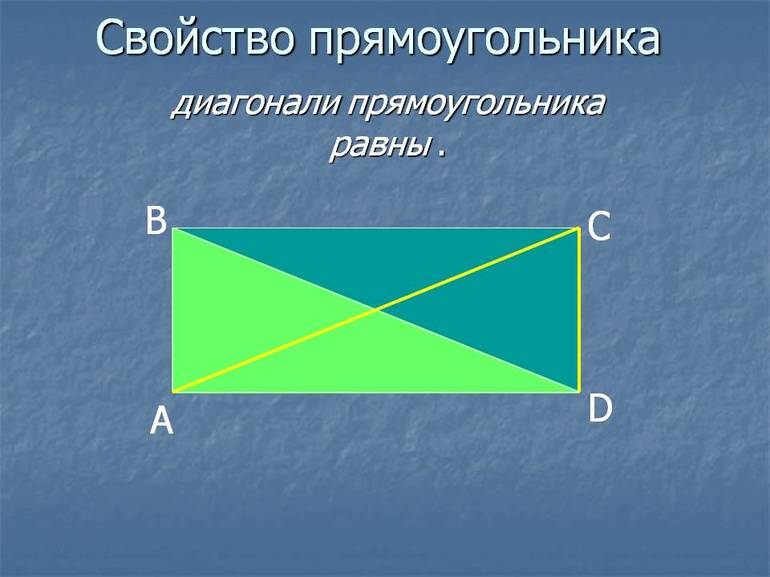
Первый и второй признаки получаются из основного определения фигуры. Третий признак является следствием доказательства теоремы, формулировка которой является следующей: диагонали прямоугольника равны. Она еще называется теоремой о диагоналях прямоугольника.

Для ее доказательства нужно начертить произвольный прямоугольник ABCD и провести в нем диагонали AC и BD. Они будут пересекаться в некоторой точке X. Они образуют прямоугольные треугольники ABC и ABD. В этом случае нужно доказать равенство треугольников. Они равны между собой: сторона АВ — общая, угол А равен В и сторона BC = AD (по равенству противоположных сторон). Из этого следует, что треугольники равны. Следовательно, их гипотенузы, которые также являются и диагоналями, равны.

Свойства фигуры

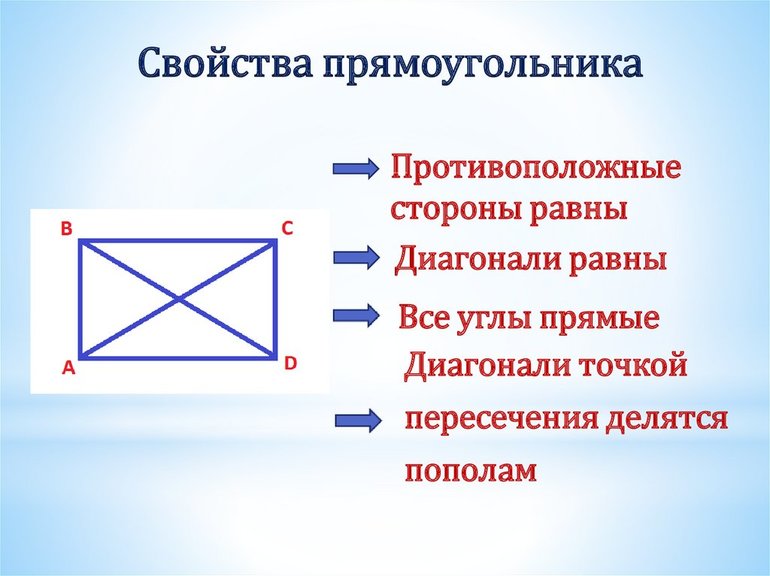
Необходимо отметить, что квадрат — правильный четырехугольник, поскольку у него все стороны равны. Результирующая формула диагонали прямоугольника будет выглядеть таким образом: d = (AB 2 + BC 2 )^(½). При решении задач применяются свойства прямоугольника:

Однако при решении задач свойств недостаточно. Для этого применяются специальные соотношения и формулы. Некоторые из них были получены из свойств фигуры. Во всех формулах будет браться радиус описанной окружности — R и ее диаметр — D, а также функция «sqrt», которая эквивалентна квадратному корню (x^(1/2) = x^(0.5)).

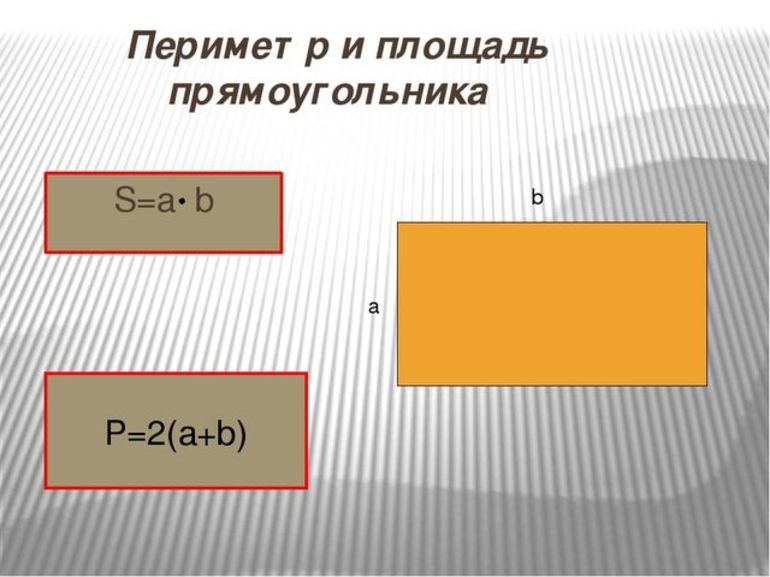
Периметр и площадь

Для удобства необходимо ввести некоторые обозначения. Диагонали следует обозначить литерой d, а противолежащие стороны — a и b, соответственно. Периметр — характеристика, соответствующая суммарному значению сторон фигуры. Очень часто ее обозначают литерой P. Существует также базовая формула: Р = 2а + 2b. Соотношение можно править таким способом: Р = 2 (a + b). Кроме того, существуют другие соотношения для определения P, когда известны некоторые параметры:

P и a (b): S = [(P * a) — 2a 2 ] / 2 = [(P * b) — 2b 2 ] / 2.

a (b) и d: S = a * sqrt[d 2 — a 2 ] = b * sqrt[d 2 — b 2 ].

Синус острого угла (Y) между двумя d и d: S = d 2 * sin (Y) / 2.

R и a (b): S = a * sqrt[4 * R 2 — a 2 ] = b * sqrt[4 * R 2 — b 2 ].

D и a (b): S = a * sqrt[D 2 — a 2 ] = b * sqrt[D 2 — b 2 ].

Для решения различных задач также могут быть полезны и другие соотношения, позволяющие найти не только диагонали, но и стороны прямоугольника.

Диагонали и стороны

Для оптимизации решения нужно знать формулы, с помощью которых можно находить одну из сторон или диагональ прямоугольника. Необходимо разобрать основные соотношения, по которым находятся стороны фигуры, когда известны следующие параметры:

Для нахождения диагонали также есть некоторые формулы. Для их применения следует знать такие параметры фигуры:

a и b: d = [a 2 + b 2 ]^(1/2).

S и a (b): d = (S 2 + a 4 )^(1/2) / a= (S 2 + b 4 )^(1/2) / b.

P и a (b): d = (P 2 — 4Pa + 8a 2 )^(1/2) / 2 = (P 2 — 4Pb + 8b 2 )^(1/2) / 2.

Однако это не все соотношения. В некоторых случаях разрешается описывать окружность вокруг фигуры. С помощью такого «геометрического хода» можно существенно упростить решение задачи. Это позволяет воспользоваться другими формулами.

Другие соотношения

Для решения задач используются и другие соотношения, которые позволяют найти параметры окружности, которая описана. Пусть дана окружность с радиусом R и диаметром D. Кроме того, известны некоторые параметры фигуры (a, b, d, P и S). С помощью формул можно найти D и R окружности при известных некоторых величинах:

a и b: R = (a 2 + b 2 )^(1/2) / 2.

P и a (b): R = (P 2 — 4Pa + 8a 2 )^(1/2) / 4 = (P 2 — 4Pb + 8b 2 )^(1/2) / 4.

S и a (b): R = (S 2 + a 4 )^(1/2) / 2a = (S 2 + b 4 )^(1/2) / 2b.

Пример решения

Пусть дана некоторая фигура, диагонали которой равны, а ее периметр равен 50. Одна из сторон a = 10. Следует провести идентификацию, а также найти такие параметры:

Данная задача является типом сложного класса, поскольку название фигуры не упоминается. Ее следует идентифицировать, а затем применить некоторые формулы для решения. Кроме того, необходимо верно выполнить 5 пункт. Однако не следует углубляться в строительную сферу. Бывают два метода укладки плитки: обычный — форма помещения является прямоугольником или квадратом, и с центра — другая фигура.

У фигуры диагонали равны, значит по третьему признаку она является прямоугольником. К нему можно применять вышеописанные формулы. Для нахождения другой стороны следует составить уравнение 2x + 2 * 10 = 50. Затем нужно перенести все известные значения в правую часть: 2х = 50 — 20. Далее можно найти переменную: х = 30 / 2 = 15 (ед.). Следует обратить внимание на написание единицы измерения. Если в условии задачи она не указана, то пишется единица измерения, которая заключается в круглые скобки. Достаточно найти только одну сторону, поскольку у прямоугольника существует свойство равенства противоположных сторон.

Значение диагоналей находится по формуле: d = [a 2 + b 2 ]^(1/2) = (15 2 + 10 2 )^(1/2) = (225 +100)^(1/2) = (325)^(1/2). Площадь можно найти таким образом: S = a * b = 15 * 10 = 150 [(ед.)^2]. Радиус вычисляется так:

R = (P 2 — 4Pa + 8a 2 )^(1/2) / 4 = (50 2 — 4 * 50 * 10 + 8 * 10 2 )^(1/2) / 4 = (1300)^(1/2) / 4 (ед.).

R = (S 2 + a 4 )^(1/2) / 2a = (150 2 + 100 4 )^(1/2) / (2 * 10) = (1300)^(1/2) / 4 (ед.).

Плитку можно укладывать обыкновенным способом, начиная не с центра, поскольку поверхность является прямоугольником. Все углы между сторонами равны между собой. Их градусная мера по 12 свойству соответствует 90.

Таким образом, при решении задач рекомендуется идентифицировать геометрическую фигуру, а затем применять к ней формулы.

Источник

Что такое диагональ квадрата и прямоугольника

9. Свойства диагоналей прямоугольника. Свойства диагоналей квадрата

Организационный этап

Вы знаете, что одному человеку бывает скучно и неинтересно. Вместе веселее, вместе быстрее, вместе сильнее. Это касается не только игры, но и работы. Сегодня наш урок пройдет под девизом: «Только вместе мы сила».

На уроке мы вспомним названия геометрических фигур, узнаем, что такое диагональ прямоугольника, будем учиться строить диагонали, познакомимся со свойствами диагоналей прямоугольника и квадрата.

Этап подготовки учащихся к активному сознательному усвоению знаний

Устный счёт

Задание

Вычислите удобным способом.

Обсуждайте задания в группах.

Задание

Петя задумал одно из чисел (10, 20, 30 или 40). Задайте ему только два вопроса, чтобы узнать, какое число он задумал.

1-й вопрос: Это число 10 или 20? Если «да», то 2-й вопрос: Это число 10? Если «нет», то Петя задумал число 20.

Если на 1-й вопрос ответ «нет», то 2-й вопрос: Это число 30? Если «нет», то Петя задумал число 40.

Задание

Иванов, Смирнов и Белов поставили во дворе автомобили. У Иванова не самый маленький автомобиль, а Смирнов не ставил автомобиль рядом с автомобилем Иванова. Где чей автомобиль?

Слева направо: автомобили Иванова, Белова, Смирнова.

Этап усвоения новых знаний

Работайте в паре, советуйтесь, проверяйте.

Рассмотрите геометрические фигуры. Какое общее название можно им дать?

Квадраты, прямоугольники, пятиугольники, шестиугольники, квадраты.

На какие группы можно разделить все многоугольники?

Можно разделить на четырехугольники и нечетырехугольники. Обратим внимание на четырехугольники. Что у них общего?

У всех четырехугольников четыре стороны, четыре вершины, четыре угла.

Начертите прямоугольник со сторонами 4 см и 2 см. Разделите его на 4 равные части.

Это можно сделать несколькими способами, соединив середины противоположных сторон или вершины противоположных сторон.

Кто знает, как называется отрезок, соединяющий противоположные вершины прямоугольника?

Отрезок, соединяющий противоположные вершины прямоугольника, называется диагональю.

Начертите квадрат со стороной 4 см. Проведите в нем диагонали.

Давайте выясним свойства диагоналей прямоугольника и квадрата. Для этого нам понадобятся циркуль и прямоугольный треугольник.

В прямоугольнике FDSA проведены диагонали. Поставим одну ножку циркуля в вершину F, другую – в противоположную вершину S. Не меняя расстояния между ножками, передвинем одну ножку циркуля в вершину A. Мы видим, что вторая ножка циркуля находится в вершине D.

Какой вывод можно сделать?

Диагонали прямоугольника равны.

Обозначим квадрат буквами MNKL. Проверьте длины диагоналей.

Диагонали квадрата равны.

Обозначим буквой О точку пересечения диагоналей в прямоугольнике.Проверим с помощью циркуля длины отрезков, получаемые при пересечении диагоналей.

Мы видим, что отрезки FО, ОS, DО и ОA равны. Сделайте вывод.

Отрезки, получаемые при пересечении диагоналей прямоугольника, равны.

Проверим отрезки, образованные при пересечении диагоналей, в квадрате.

Отрезки, получаемые при пересечении диагоналей квадрата, равны.

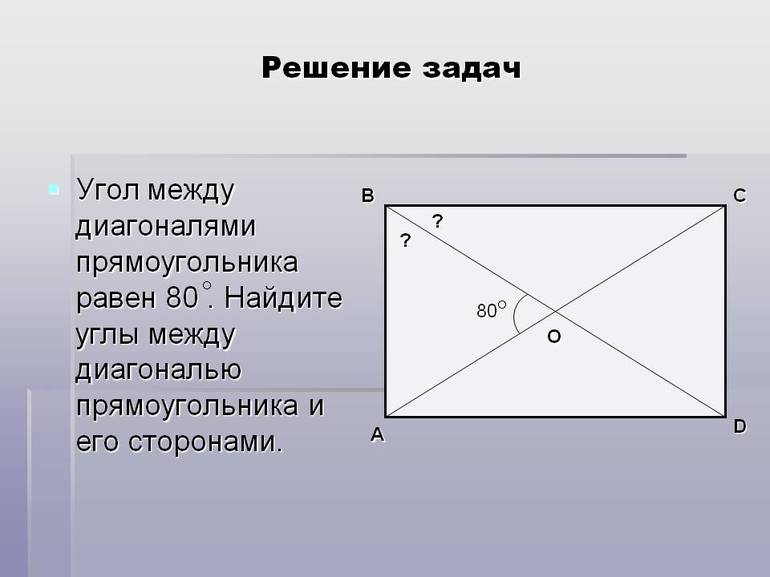
Какие углы получаются при пересечении диагоналей?

При пересечении диагоналей прямоугольника получаются острые и тупые углы.

При пересечении диагоналей квадрата получается 4 прямых угла.

Запишем в таблицу в свойства квадрата.

Какие свойства диагоналей прямоугольника и квадрата похожи?

Первое свойство: диагонали равны.

Второе свойство: отрезки, получаемые при пересечении диагоналей, равны.

2) Отрезки, получаемые при пересечении диагоналей, равны.

3) При пересечении диагоналей получается 4 прямых угла.

Закрепление материала

Начертите в тетради прямоугольник ABCD со сторонами 6 см и 3 см. Проведите диагонали, измерьте их и сделайте вывод.

Диагональ AC равна 6 см 7 мм, диагональ BD равна 6 см 7 мм. Диагонали прямоугольника AC и BD равны.

А теперь проделайте те же самые действия с квадратом ZXEP со стороной 3 см.

Диагональ ZE равна 4 см 2 мм и диагональ XP равна 4 см 2 мм. Диагонали квадрата ZE и XP равны.

Проверьте второе свойство диагоналей прямоугольника и квадрата.

Отрезки, получаемые при пересечении диагоналей, равны.

Чему равна площадь прямоугольника со сторонами 5 см и 3 см?

5 · 3 = 15 (см²) – площадь прямоугольника

Площадь прямоугольника 15 см².

Площадь прямоугольника 48 см², а длина одной из сторон 12 см. Чему равен периметр прямоугольника?

Проверьте свое решение.

1) 48 : 12 = 4 (см) – длина второй стороны прямоугольника

2) (12 + 4) · 2 = 32 (см) – периметр прямоугольника

Ответ: 32 сантиметра.

Этап подведения итогов

Какие вопросы вы бы хотели задать друг другу по теме урока? Сформулируйте их.

Рефлексия

Когда вам работать легче и комфортнее: в паре, группе или одному?

Остались вопросы по теме? Наши репетиторы готовы помочь!

Подготовиться к ЕГЭ, ОГЭ и другим экзаменам

Подготовиться к поступлению в любой ВУЗ страны

Источник

Квадрат — определение и свойства

Квадрат — это прямоугольник, у которого все стороны равны.
Можно дать и другое определение квадрата:
квадрат — это ромб, у которого все углы прямые.

Получается, что квадрат обладает всеми свойствами параллелограмма, прямоугольника и ромба.

Перечислим свойства квадрата:

Разберем несколько простых задач на тему «Квадрат». Все они взяты из Банка заданий ФИПИ.

Очевидно, радиус окружности равен половине диагонали квадрата.

Диаметр окружности равен стороне квадрата.

Чуть более сложная задача. Нарисуйте окружность, вписанную в данный квадрат, то есть касающуюся всех его сторон. Вы увидите, что диаметр этой окружности равен стороне квадрата.

Считаем стороны клеток равными единице. Четырехугольник — квадрат. Все его стороны равны, все углы — прямые. Как и в предыдущей задаче, радиус окружности, вписанной в квадрат, равен половине его стороны.

Источник

Прямоугольник

Прямоугольник — параллелограмм, у которого все углы прямые.

Частным случаем прямоугольника является квадрат.

Свойства прямоугольника

1. Так как прямоугольник – это параллелограмм, то все свойства параллелограмма верны и для прямоугольника.

Помимо этого:

2. Стороны прямоугольника являются его высотами.

3. Диагонали прямоугольника равны.

4. Квадрат диагонали прямоугольника равен сумме квадратов двух его соседних сторон.

5. Около любого прямоугольника можно описать окружность, при этом диагональ прямоугольника равна диаметру описанной окружности.

Признаки параллелограмма

Параллелограмм является прямоугольником, если выполняется любое из условий:

1. Диагонали параллелограмма равны.

2. Квадрат диагонали параллелограмма равен сумме квадратов соседних сторон.

3. Все углы параллелограмма равны.

Площадь прямоугольника

Смотрите также таблицу-шпаргалку «Площади простейших фигур» здесь.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Источник

Прямоугольник, свойства, признаки и формулы

Прямоугольник, свойства, признаки и формулы.

Прямоугольник – это четырехугольник, у которого все углы прямые (каждый из углов равен 90 градусам).

Прямоугольник (понятие, определение):

Прямоугольник – это четырехугольник, у которого все углы прямые (каждый из углов равен 90 градусам).

Прямоугольник – это четырехугольник, у которого каждый угол является прямым.

Прямоугольник – это четырехугольник, у которого две противоположные стороны равны между собой и все четыре угла равны между собой и каждый из них составляет 90 градусов.

Рис. 1. Прямоугольник

В свою очередь четырёхугольник (греч. τετραγωνον) – это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин), никакие три из которых не лежат на одной прямой, и четырёх отрезков (сторон), последовательно соединяющих эти точки.

Длинную сторону прямоугольника называют длиной прямоугольника, а короткую – шириной прямоугольника.

Свойства прямоугольника:

1. Прямоугольник является параллелограммом – его противоположные стороны попарно параллельны.

Рис. 2. Прямоугольник

2. Противоположные стороны прямоугольника равны.

Рис. 3. Прямоугольник

3. Стороны прямоугольника являются его высотами.

4. Прилегающие стороны прямоугольника всегда перпендикулярны.

Рис. 4. Прямоугольник

5. Каждый угол прямоугольника прямой и равен 90 градусам. Сумма всех углов прямоугольника составляет 360 градусов.

Рис. 5. Прямоугольник

6. Диагонали прямоугольника равны.

Рис. 6. Прямоугольник

Рис. 7. Прямоугольник

8. Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон (что вытекает из теоремы Пифагора).

Рис. 8. Прямоугольник

9. Диагонали прямоугольника делятся точкой пересечения пополам.

10. Около любого прямоугольника можно описать окружность. Диагональ прямоугольника является диаметром описанной окружности.

АС и BD – диаметр описанной окружности и диагональ прямоугольника

11. Точка пересечения диагоналей называется центром прямоугольника и является центром описанной окружности.

12. Прямоугольник может содержать вписанную окружность и только одну, если все его стороны равны, т.е. он является квадратом.

Признаки прямоугольника:

– если диагонали параллелограмма равны, то он является прямоугольником;

– если квадрат диагонали параллелограмма равен сумме квадратов смежных сторон, то он (параллелограмм) является прямоугольником;

– если углы параллелограмма равны, то он является прямоугольником.

Формулы прямоугольника:

Пусть a – длина прямоугольника, b – ширина прямоугольника, d – диагональ и диаметр описанной окружности прямоугольника, R – радиус описанной окружности прямоугольника, P – периметр прямоугольника, S – площадь прямоугольника.

Формула стороны прямоугольника (длины и ширины прямоугольника):

,

,

,

.

Формула диагонали прямоугольника:

,

Формулы периметра прямоугольника:

Формулы площади прямоугольника:

Формула радиуса окружности, описанной вокруг прямоугольника:

.

Примечание: © Фото https://www.pexels.com, https://pixabay.com

Мировая экономика

Справочники

Востребованные технологии

Поиск технологий

О чём данный сайт?

Настоящий сайт посвящен авторским научным разработкам в области экономики и научной идее осуществления Второй индустриализации России.

Он включает в себя:
– экономику Второй индустриализации России,
– теорию, методологию и инструментарий инновационного развития – осуществления Второй индустриализации России,
– организационный механизм осуществления Второй индустриализации России,
– справочник прорывных технологий.

Мы не продаем товары, технологии и пр. производителей и изобретателей! Необходимо обращаться к ним напрямую!

Мы проводим переговоры с производителями и изобретателями отечественных прорывных технологий и даем рекомендации по их использованию.

О Второй индустриализации

Осуществление Второй индустриализации России базируется на качественно новой научной основе (теории, методологии и инструментарии), разработанной авторами сайта.

Конечным результатом Второй индустриализации России является повышение благосостояния каждого члена общества: рядового человека, предприятия и государства.

Вторая индустриализация России есть совокупность научно-технических и иных инновационных идей, проектов и разработок, имеющих возможность быть широко реализованными в практике хозяйственной деятельности в короткие сроки (3-5 лет), которые обеспечат качественно новое прогрессивное развитие общества в предстоящие 50-75 лет.

Та из стран, которая первой осуществит этот комплексный прорыв – Россия, станет лидером в мировом сообществе и останется недосягаемой для других стран на века.

Источник