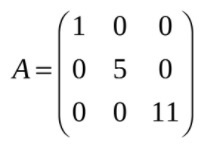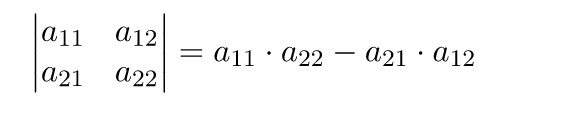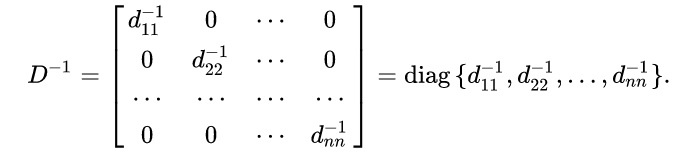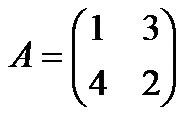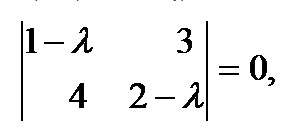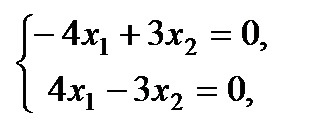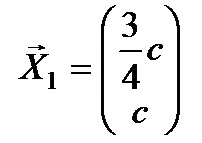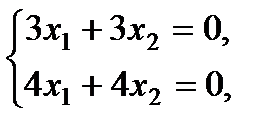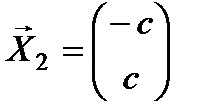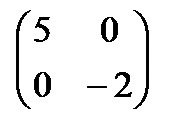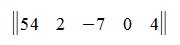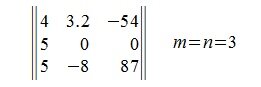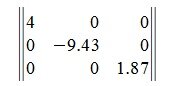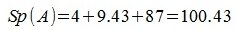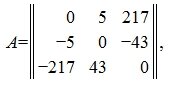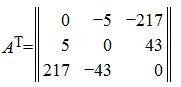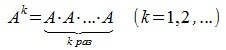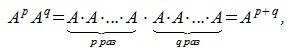Что такое диагональная матрица

Диагональные матрицы: определение и свойства

Обновлено: 20 Июля 2021

Матрица — это прямоугольная таблица чисел, состоящая из определенного количества строк и столбцов. Существует множество матричных видов, и один из них — диагональный. Разберемся, что он из себя представляет.

Что такое диагональная матрица

У диагональной матрицы элементы, расположенные вне главной диагонали, равны нулю.

Напомним, что матрица считается квадратной, если количество строк равно количеству столбцов (m = n).

Особенности и свойства

Для начала нужно понять, что такое матричный определитель.

Определитель (детерминант) — это некоторая величина, с которой можно сопоставить любую квадратную матрицу.

Определитель А = (2×2), к примеру, вычисляется по формуле:

Из этого следует свойство №1: определитель диагональной матрицы равен произведению ее диагональных элементов.

Свойство №2: обратная матрица для диагональной равна:

Свойство №3: ранг равен количеству ненулевых диагональных элементов.

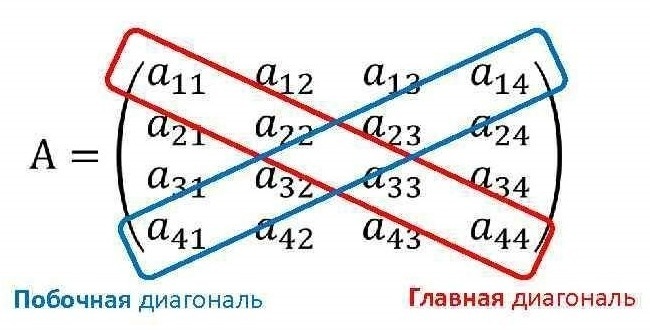
Главная и побочная диагонали

Побочной диагональю называют диагональ элементов от правого верхнего угла до нижнего левого. Эти диагонали параллельны друг другу.

Частные случаи диагональных матриц

Существуют три основных подвида: единичная, нулевая, скалярная.

Единичная матрица

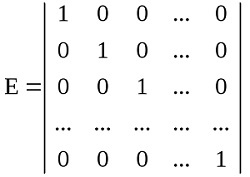
У единичной матрицы все диагональные элементы равны единице.

В формулах ее обозначают буквой Е.

Нулевая матрица

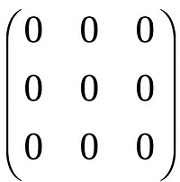
В нулевой матрице все элементы, в том числе диагональные, равны нулю.

В формулах ее обозначают цифрой 0.

Скалярная матрица

В скалярной матрице все элементы на главной диагонали равны друг другу.

В некоторых случаях говорят, что скалярная матрица — это произведение скаляра на единичную матрицу Е. В ней диагональные элементы могут быть как положительными, так и отрицательными.

Примеры решения диагональных матриц

Иногда недиагональная матрица может быть приведена к диагональному виду.

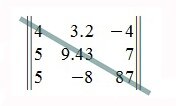
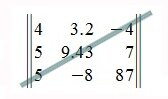
Условие: дана матрица А

Задача: привести к диагональному виду.

Решение: характеристическое уравнение равно

Таким образом, диагональная матрица имеет вид:

Изучение данных математических объектов имеет свои подводные камни. Если у вас нет времени на учебу, Феникс.Хелп может помочь вам с решением контрольных, самостоятельных и иных проверочных работ.

Источник

Матрицы. Виды матриц

Матрицей называется прямоугольная таблица из чисел с некоторым количеством m строк и с некоторым количеством n столбцов. Числа m и n называются порядками или размерами матрицы.

Матрица порядка m × n записывается в форме:

или (i=1,2. m; j=1,2. n).

Числа a_ij входящие в состав данной матрицы называются ее элементами. В записи a_ij первый индекс i означает номер строки, а второй индекс j— номер столбца.

Матрица строка

Матрица размером 1×n, т.е. состоящая из одной строки, называется матрицей-строкой. Например:

Матрица столбец

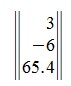
Матрица размером m×1, т.е. состоящая из одного столбца, называется матрицей-столбцом. Например

Нулевая матрица

Квадратная матрица

Матрица A порядка m×n называется квадратной матрицей, если количество строк и столбцов совпадают: m=n. Число m=n называется порядком квадратной матрицы. Например:

Главная диагональ матрицы

Побочная диагональ матрицы

Диагональная матрица

Квадратная матрица называется диагональной, если элементы, расположенные вне главной диагонали равны нулю. Пример диагональной матрицы:

Единичная матрица

След матрицы

Сумма главных диагональных элементов матрицы A называется следом матрицы и обозначается Sp A или Tr A. Например:

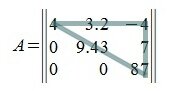
Верхняя треугольная матрица

Нижняя треугольная матрица

Квадратная матрица порядка n×n называется нижней треугольной матрицей, если равны нулю все элементы матрицы, расположенные над главной диагональю, т.е. a_ij=0, при всех i T ).

Cтолбцы матрицы A образуют пространство столбцов матрицы и обозначаются через R(A).

Ядро или нуль пространство матрицы

Противоположная матрица

Для любой матрицы A сущеcтвует противоположная матрица -A такая, что A+(-A)=0. Очевидно, что в качестве матрицы -A следует взять матрицу (-1)A, элементы которой отличаются от элементов A знаком.

Кососимметричная (Кососимметрическая) матрица

Кососимметричной называется квадратная матрица, которая отличается от своей транспонированной матрицы множителем −1:

В кососимметричной матрице любые два элемента, расположенные симметрично относительно главной диагонали отличаются друг от друга множителем −1, а диагональные элементы равны нулю.

Пример кососимметрической матрицы:

Разность матриц

Разностью C двух матриц A и B одинакового размера определяется равенством

Для обозначения разности двух матриц используется запись:

Степень матрицы

Пусть квадратная матрица размера n×n. Тогда степень матрицы определяется следующим образом:

где E-единичная матрица.

Из сочетательного свойства умножения следует:

где p,q— произвольные целые неотрицательные числа.

Симметричная (Симметрическая) матрица

Матрица, удовлетворяющая условию A=A T называется симметричной матрицей.

Для симметричных матриц имеет место равенство:

Источник