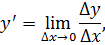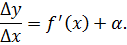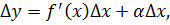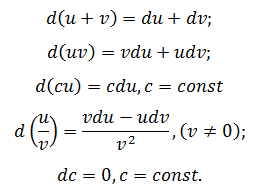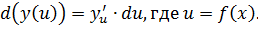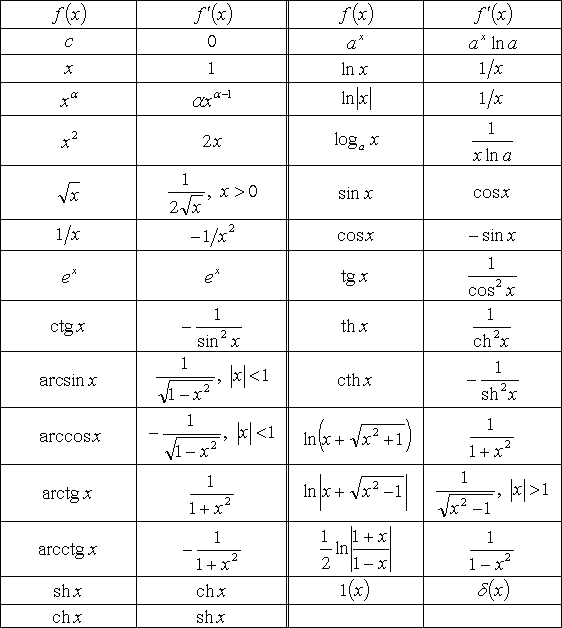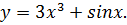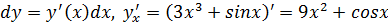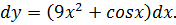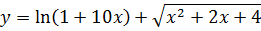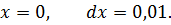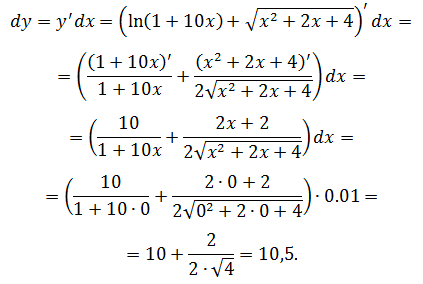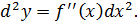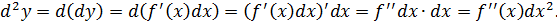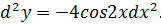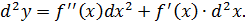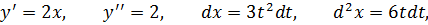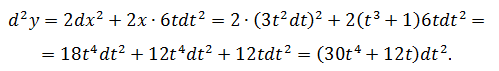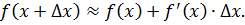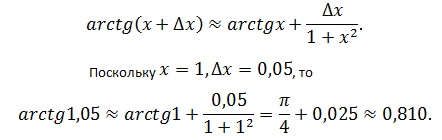Что такое дифференциал функции для чайников
При выполнении некоторых расчётов в исследованиях, проектировании, анализе полученных опытных путём данных часто возникает необходимость предварительной прикидки результата, которую удобно выполнять, используя дифференциал функции. Приближённые вычисления, выполненные с его помощью, могут дать новые направления дальнейшего изучения объектов и их разработок.
Понятие и геометрический смысл дифференциала
Пусть y = f (x) имеет производную
Применяя свойства предела функции, получают равенство
После умножения обеих частей на приращение аргумента Δx, образуется тождество:
в котором в правой части записано слагаемое, являющееся бесконечно малой одного порядка с Δx, далее идет слагаемое более высокого порядка.
Определение 1
Дифференциалом функции y = f (x) первого порядка называется главная часть её приращения f′(x)Δx, которую обозначают dy (или d(f(x)).
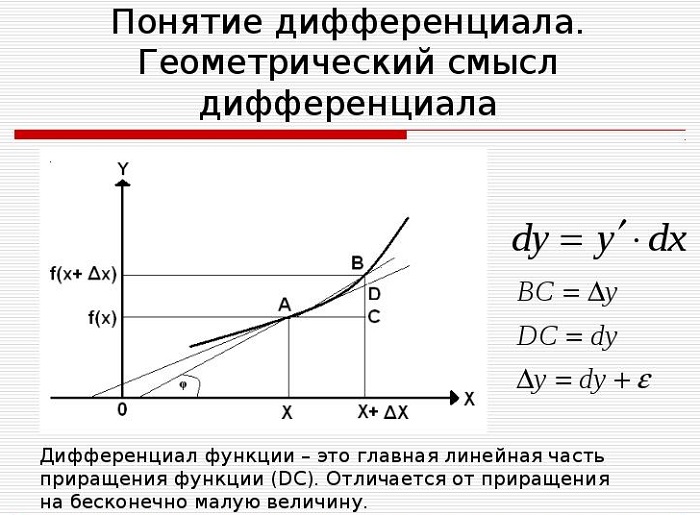
Для наглядного представления и понимания определения рассматривается касательная к графику функции y = f(x) в точке x. Когда значение переменной сдвигается по построенной прямой (получает приращение) на некоторую малую величину Δx, значение второй координаты точки тоже меняется.
Значит, дифференциал функции y = f(x) в точке x равен приращению ординаты касательной, когда её абсцисса меняется на величину Δx.
Определение 2
Дифференциал от дифференциала называется дифференциалом второго порядка. Таким же рекуррентным образом вводятся понятия дифференциалов более высоких порядков.
Формы записи дифференциала
Для нахождения дифференциала независимой переменной рассматривают функцию y = x, учитывая, что x’ = 1, а, следовательно:
Отсюда получается формула:
Для второго порядка вводится обозначение d 2 y.
Свойства дифференциала
Существующая таблица производных помогает выделить некоторые свойства дифференциалов, например, для суммы, произведения, частного получаются следующие правила:
Одним из важных свойств является инвариантность (неизменность) формы записи, независимо от того, является ли функция элементарной или композицией элементарных (сложной). Фактически,
Примеры решения задач
Задача №1
Найти дифференциал функции
Задача №2
Вычислить значение дифференциала функции
В помощь студентам создан онлайн калькулятор, который позволяет ввести функцию, нажать кнопку и получить форму или значение дифференциала.
Если dx есть константа, то для высших порядков имеет место следующая формула:
Этот результат вытекает непосредственно из определения:
Задача №3
Найти d 2 y, если y = cos2x и x – независимая переменная.
Если x – функция от некоторой другой независимой переменной, то свойство инвариантности перестаёт работать, следовательно,
Задача №4
Найти d 2 y, если y = x 2 и x = t 3 + 1, t – независимый аргумент.
Нетрудно заметить, что если выразить y напрямую через t, то получится тот же результат.
с высокой степенью точности можно вычислить приращение любой дифференцируемой зависимости.
Раскрыв Δy, сделав соответствующие преобразования, приходят к формуле приближённых вычислений:
Задача №5
Вычислить приближённо arctg1,05.
Пусть f(x) = arctg x. Тогда
Полный дифференциал функции
Математика не ограничивается множеством функций одного независимого аргумента. Рассматриваются зависимости от двух и более переменных.
Определения похожи, отличается вид главной части. Рассматриваются несколько слагаемых.
Например, если z = f(x;y) то
Последнее равенство есть формула полного дифференциала. Для функции нескольких переменных сохраняется принцип построения.
Если рассматривают приращения только по одной переменной, то приходят к понятию частных дифференциалов.
Заключение
Высшая математика позволяет находить приближённо общий корень системы уравнений, пользуясь дифференциальным исчислением, делать прикидку результатов, прогнозировать получаемое.
Производная как смысл жизни или что такое дифференциал(d)
Пролог:
Эта одна из статей серии «Производная как смысл жизни», сначала я хотел сделать одну огромную статью про почти все темы по дифференцированию, но я передумал и сделаю несколько статей, возможно так даже будет легче для людей которые пытаются найти конкретную для себя тему.
Начало
Для начала лучше ознакомиться со статьей о самой прозводной (скоро будет). Ну если вы ознакомились, или уже были ознакомлены то идем дальше.
Как мы уже знаем формула записи производной выглядит так:
Мы должны понимать, что если мы уберем предел, то к f'(x) прибавиться коофициент, я ее называю «неточность».
Так же вполне логично, что при Δx->0, β->0, так как чем меньше мы делаем разницу между x и x₀, тем меньше значение «неточности»(в статье о производной об этом подробнее рассказано).
Теперь выразим из этого равенства приращение функции(Δy):
И на этом следует пока остановиться и рассмотреть график.
Смотрим дифференциалу в лицо
Расмотрим такой график:
Как мы знаем производная в точке равняется значению тангенса угла в этой точке, то есть f'(x)=tg(α). Так что давайте обозначим производную, ну и приращения которыми она ограничена.
Зная это введем обозначение на графике:
Вернемся к равенству
BD = Δy и мы знаем, что BD = BC + CD, а значит Δy = BC + CD, где BC мы назвали главной линейной частью приращения функции(dy), следовательно Δy = dy + βΔx.
Из формулы мы понимаем, что dy=f'(x)Δx.
Хорошо, мы определили чему равен дифференциал функции, а что же тогда является дифференциалом независимой пременной функции(аргумента).
Графически мы видим, что Δx никак не разделена касательной, то есть Δx это полное приращение функции, а значит dx = Δx.
Так же мы можем найти по формуле: dx = (x)’Δx = 1*Δx = Δx
И зная, что dy = f'(x)dx, мы можем выразить производную: f'(x)=dy/dx.
Немного пределов
Добавим с левой части и с правой предел
В самом начале мы сказали, что если β->0, то Δx->0 и наборот, а значит:
Зная, что f'(x)Δx = dy, мы делаем вывод, что:
Дифференциал функции определение, виды, свойства, формула полного дифференциала функции, геометрический смысл, правило применения, примеры решения уравнений
При выполнении некоторых расчётов в исследованиях, проектировании, анализе полученных опытных путём данных часто возникает необходимость предварительной прикидки результата, которую удобно выполнять, используя дифференциал функции.
Приближённые вычисления, выполненные с его помощью, могут дать новые направления дальнейшего изучения объектов и их разработок.
Понятие и геометрический смысл дифференциала
Пусть y = f (x) имеет производную
Применяя свойства предела функции, получают равенство
После умножения обеих частей на приращение аргумента Δx, образуется тождество:
в котором в правой части записано слагаемое, являющееся бесконечно малой одного порядка с Δx, далее идет слагаемое более высокого порядка.
Определение 1
Дифференциалом функции y = f (x) первого порядка называется главная часть её приращения f′(x)Δx, которую обозначают dy (или d(f(x)).
Для наглядного представления и понимания определения рассматривается касательная к графику функции y = f(x) в точке x. Когда значение переменной сдвигается по построенной прямой (получает приращение) на некоторую малую величину Δx, значение второй координаты точки тоже меняется.
Значит, дифференциал функции y = f(x) в точке x равен приращению ординаты касательной, когда её абсцисса меняется на величину Δx.
Определение 2
Дифференциал от дифференциала называется дифференциалом второго порядка. Таким же рекуррентным образом вводятся понятия дифференциалов более высоких порядков.
Формы записи дифференциала
Для нахождения дифференциала независимой переменной рассматривают функцию y = x, учитывая, что x’ = 1, а, следовательно:
Отсюда получается формула:
Для второго порядка вводится обозначение d 2 y.
Свойства дифференциала
Существующая таблица производных помогает выделить некоторые свойства дифференциалов, например, для суммы, произведения, частного получаются следующие правила:
Одним из важных свойств является инвариантность (неизменность) формы записи, независимо от того, является ли функция элементарной или композицией элементарных (сложной). Фактически,
Примеры решения задач
Задача №1
Найти дифференциал функции
Задача №2
Вычислить значение дифференциала функции
В помощь студентам создан онлайн калькулятор, который позволяет ввести функцию, нажать кнопку и получить форму или значение дифференциала.
Если dx есть константа, то для высших порядков имеет место следующая формула:
Этот результат вытекает непосредственно из определения:
Задача №3
Найти d 2 y, если y = cos2x и x – независимая переменная.
Если x – функция от некоторой другой независимой переменной, то свойство инвариантности перестаёт работать, следовательно,
Задача №4
Найти d 2 y, если y = x 2 и x = t 3 + 1, t – независимый аргумент.
Нетрудно заметить, что если выразить y напрямую через t, то получится тот же результат.
с высокой степенью точности можно вычислить приращение любой дифференцируемой зависимости.
Раскрыв Δy, сделав соответствующие преобразования, приходят к формуле приближённых вычислений:
Задача №5
Вычислить приближённо arctg1,05.
Пусть f(x) = arctg x. Тогда
Полный дифференциал функции
Математика не ограничивается множеством функций одного независимого аргумента. Рассматриваются зависимости от двух и более переменных.
Определения похожи, отличается вид главной части. Рассматриваются несколько слагаемых.
Например, если z = f(x;y) то
Последнее равенство есть формула полного дифференциала. Для функции нескольких переменных сохраняется принцип построения.
Если рассматривают приращения только по одной переменной, то приходят к понятию частных дифференциалов.
Заключение
Высшая математика позволяет находить приближённо общий корень системы уравнений, пользуясь дифференциальным исчислением, делать прикидку результатов, прогнозировать получаемое.
Лекция по высшей математике»Дифференциал функции»(для 26 гр.)
«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Дифференциал называют также дифференциалом первого порядка.
Основные теоремы о дифференциалах. Таблица дифференциалов.
Теорема 1. Дифференциал суммы, произведения и частного двух дифференцируемых функций определяется формулами:
Теорема 2. Дифференциал сложной функции равен произведению производной этой функции по промежуточной переменной на дифференциал этой промежуточной переменной.
Применение дифференциала в приближенных вычислениях
Производные высших порядков.
Производная у’ = f ‘(х) функции у = f ( x ) есть также функция от х и называется производной первого порядка.
Производные порядка выше первого называются производными высших порядков.
Механический смысл производной второго порядка
Вторая производная от пути по времени есть величина ускорения прямолинейного движения точки, т. е. = V¢ = а.
Дифференциалы высших порядков.
Определение. Дифференциал от дифференциала функции называется ее вторым дифференциалом или дифференциалом второго порядка. Обозначение: d ² y = d ( dy ).
При вычислении второго дифференциала учтем, что dx не зависит от х и при дифференцировании выносится за знак производной как постоянный множитель.
Подобным же образом можно найти третий дифференциал от данной функции:
Свойства дифференциалов высших порядков.
Дифференциалы высших порядков не обладают свойством инвариантности.
Возрастание и убывание функций
Определение. Точка х0 называется точкой максимума функции f (x) , если в некоторой окрестности точки х0 выполняется неравенство f (x) ≤ f (x0 ) (рис. 11).
Определение. Точка х1 называется точкой минимума функции f (x) , если в некоторой окрестности точки х1 выполняется неравенство f (x) ≥ f (x1 ) (рис. 11).
симум и минимум функции объединяются общим названием экстремума функции.
Точки, в которых выполнено необходимое условие экстремума, т.е. производная равна нулю или не существует, называются критическими (или стационарными). Обращаем внимание на то, что эти точки должны входить в область определения функции.
Таким образом, если в какой-либо точке имеется экстремум, то эта точка критическая. Очень важно заметить, что обратное утверждение не верно. Критическая точка вовсе не обязательно будет точкой экстремума.
Правило исследования функции на экстремум.
1. Найти производную и критические точки, в которых =0 или не существует, а сама функция непрерывна, и которые лежат внутри области определения функции.
2а. Определить знак слева и справа от каждой критической точки.
Если при переходе аргумента х через критическую точку хо:
3) не меняет знака, то в точке хо нет экстремума.
2б. Найти вторую производную и определить ее знак в каждой критической точке.
Если в критической точке хо, где :
1. Найти и точки х, в которых =0 или не существует, а кривая непрерывна и которые лежат внутри области ее расположения.
2. Определить знак слева и справа от каждой из этих точек. Исследуемая точка х будет абсциссой точки перегиба, если по разные стороны от нее имеет разные знаки.
Интервалы, где кривая выпукла вверх и где она выпукла вниз, определяются из условия, что их границами могут быть только абсциссы точек перегиба, точки разрыва и граничные точки области расположения кривой.
Асимптотой кривой называется такая прямая, к которой неограниченно приближается точка кривой при неограниченном удалении ее от начала координат.
Для нахождения асимптот пользуются следующими положениями:
Правило исследования функции на экстремум с помощью второй производной:
1.Находят первую производную f ‘ (x).
2.Находят действительные корни уравнения f ‘(x)=0 (критические точки).
3.Находят вторую производную f » (x).
4.Во вторую производную подставляют поочередно все критические значения; если при этой подстановке вторая производная окажется положительной, то в этой точке функция имеет минимум; если же вторая производная окажется отрицательной, то функция имеет максимум. Если при подстановке получится нуль, то исследование нужно продолжить с помощью первой производной.
Например 1. Исследовать на экстремум функцию у = 1/3х 3 – 2х 2 +3х + 1.
2)Решаем уравнение х 2 — 4х + 3= 0, его корни х1= 1, х2= 3 – критические точки;
3. Определяя знак у’, находим экстремум; при х = 1функция достигает максимума, а при х =3 функция достигает минимума.
4. Находим значение функции в точках экстремума у(1) =7/3, у(3) =1.
Например 2. Исследовать на экстремум с помощью второй производной функцию
3.Находим вторую производную у» = 2х – 5;
4.Во вторую производную подставляем поочередно критические значения:
Задания для самостоятельной работы.
Найти дифференциал второго порядка для функций: а) у = sin x∙ ln 3x, б) у = 6 х +2,5х 6
Исследовать на выпуклость, вогнутость и точки перегиба функции:
Найти промежутки выпуклости и вогнутости кривой у = х 4 – 2х 3 + 36х 2 – х + 7.
Что такое дифференциал функции для чайников
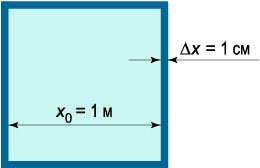
Заметим, что в данном примере коэффициент \(A\) равен значению производной функции \(S\) в точке \(
Коэффициент \(A\) главной части приращения функции в точке \(
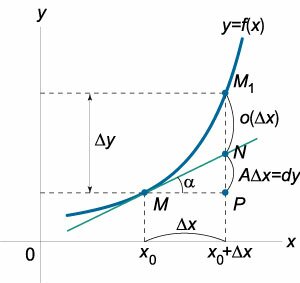
На рисунке \(2\) схематически показана разбивка приращения функции \(\Delta y\) на главную часть \(A\Delta x\) (дифференциал функции) и член высшего порядка малости \(\omicron\left( <\Delta x>\right)\).
Касательная \(MN\), проведенная к кривой функции \(y = f\left( x \right)\) в точке \(M\), как известно, имеет угол наклона \(\alpha\), тангенс которого равен производной: \[\tan \alpha = f’\left( <