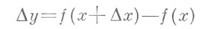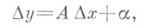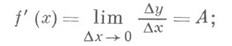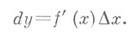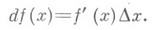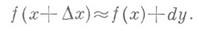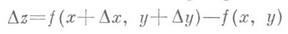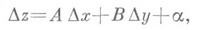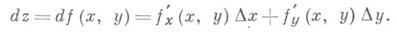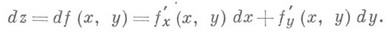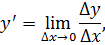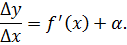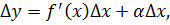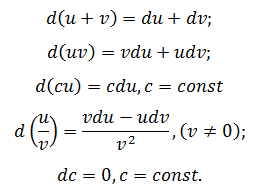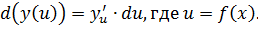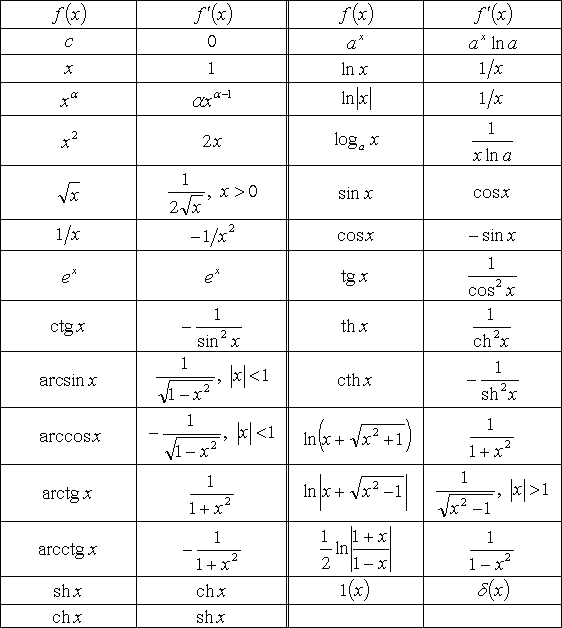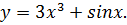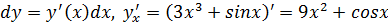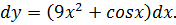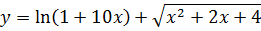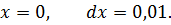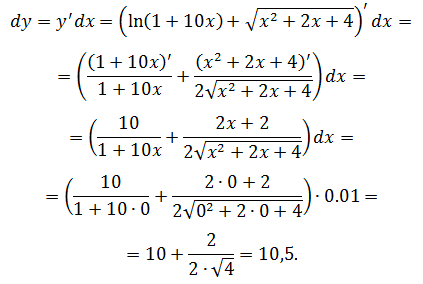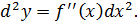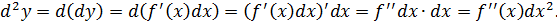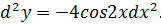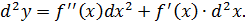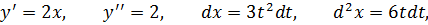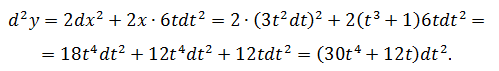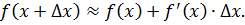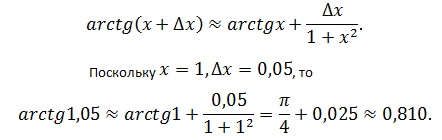Что такое дифференциал матанализ
Производная как смысл жизни или что такое дифференциал(d)
Пролог:
Эта одна из статей серии «Производная как смысл жизни», сначала я хотел сделать одну огромную статью про почти все темы по дифференцированию, но я передумал и сделаю несколько статей, возможно так даже будет легче для людей которые пытаются найти конкретную для себя тему.
Начало
Для начала лучше ознакомиться со статьей о самой прозводной (скоро будет). Ну если вы ознакомились, или уже были ознакомлены то идем дальше.
Как мы уже знаем формула записи производной выглядит так:
Мы должны понимать, что если мы уберем предел, то к f'(x) прибавиться коофициент, я ее называю «неточность».
Так же вполне логично, что при Δx->0, β->0, так как чем меньше мы делаем разницу между x и x₀, тем меньше значение «неточности»(в статье о производной об этом подробнее рассказано).
Теперь выразим из этого равенства приращение функции(Δy):
И на этом следует пока остановиться и рассмотреть график.
Смотрим дифференциалу в лицо
Расмотрим такой график:
Как мы знаем производная в точке равняется значению тангенса угла в этой точке, то есть f'(x)=tg(α). Так что давайте обозначим производную, ну и приращения которыми она ограничена.
Зная это введем обозначение на графике:
Вернемся к равенству
BD = Δy и мы знаем, что BD = BC + CD, а значит Δy = BC + CD, где BC мы назвали главной линейной частью приращения функции(dy), следовательно Δy = dy + βΔx.
Из формулы мы понимаем, что dy=f'(x)Δx.
Хорошо, мы определили чему равен дифференциал функции, а что же тогда является дифференциалом независимой пременной функции(аргумента).
Графически мы видим, что Δx никак не разделена касательной, то есть Δx это полное приращение функции, а значит dx = Δx.
Так же мы можем найти по формуле: dx = (x)’Δx = 1*Δx = Δx
И зная, что dy = f'(x)dx, мы можем выразить производную: f'(x)=dy/dx.
Немного пределов
Добавим с левой части и с правой предел
В самом начале мы сказали, что если β->0, то Δx->0 и наборот, а значит:
Зная, что f'(x)Δx = dy, мы делаем вывод, что:
ДИФФЕРЕНЦИАЛ
— главная линейная часть приращения функции.
1) Действительная функция y = f
(при условии, что точка х+Ах лежит в упомянутой окрестности) может быть представлено в виде
где 
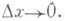
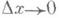
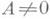
Для функции, дифференцируемой в точке х, 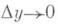
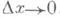
Существуют непрерывные, но не дифференцируемые функции.
Кроме обозначения dy используется обозначение df(x);тогда предыдущее равенство принимает вид
Приращение аргумента Ах обозначается также через dx и наз. дифференциалом независимого переменного. Поэтому можно писать
Отсюда f(x)=dyldx, т. е. производная равна отношению Д. dy и dx. Если А=0, то 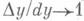

Конечно, такое рассуждение имеет ценность, если можно оценить соответствующую погрешность.
При этом a= Dу-dy, т. е. значение |a| совпадает с длиной отрезка TS.
2) Определение дифференцируемости и Д. естественным образом обобщается на действительные функции от пдействительных переменных. Напр., в случ. п=2 действительная функция z=f(x, у)наз. дифференцируемой в точке ( х, у )по совокупности переменных хи у, если она определена в нек-рой окрестности этой точки и ее полное приращение
может быть представлено в виде
где Аи В- некоторые числа, 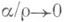
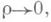

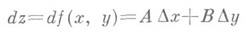
Если f(x, у )дифференцируема в точке ( х, у), то oн непрерывна в этой точке и имеет в ней конечные частные производные
Приращения Ах и Ау независимых переменных, как и в случае одного переменного, обозначаются dx и dу По этой причине можно написать
Существование конечных частных производных, во обще говоря, не влечет дифференцируемости функции (даже если предполагать заранее ее непрерывность) здесь нарушается аналогия с функциями одного переменного.
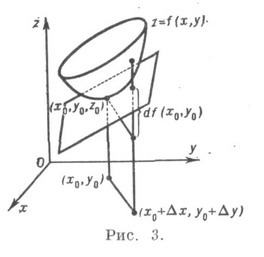
Если функция f(x, у )имеет в точке ( х, у )частную производную по х, то произведение fx(x, y)dx наз. частным дифференциалом по х;аналогично, f’y(x, y)dy есть частный Д. по у. Если функция дифференцируема, то ее полный Д. равен сумме частных Д. Геометрически полный Д. df(x0, у 0 )есть приращение аппликаты касательной плоскости поверхности z-f(x, у )в точке ( х 0, у 0, z0), где z0=f(z0, у 0 )(см. рис. 3).
Это показывает, в частности, что не всякое выражение 
Выражение Adx+Bdy является полным Д. нек-рой функции z=f(x, у), в односвязной открытой области D, если ( х, у )и В( х, у )непрерывны в этой области и удовлетворяют условию А’ =В’ Х и при этом а) А’y и В’ х непрерывны или б) ( х, у) и В( х, у) дифференцируемы по совокупности переменных хи увсюду в D(см. [7], [8]).
О Д. действительных функций одного или нескольких действительных переменных и о Д. высших порядков см. также Дифференциальное исчисление.
3) Пусть функция f(x)определена на нек-ром множестве Едействительных чисел, х- предельная точка этого множества, 


Подобным же образом вводится Д. по множеству для действительных функций многих действительных переменных.
4) Все эти определения дифференцируемости и Д. почти без изменений распространяются соответственно на комплексные функции одного или нескольких действительных переменных, на действительные и комплексные вектор-функции одного или нескольких действительных переменных, на комплексные функции и вектор-функции одного или нескольких комплексных переменных. В функциональном анализе они распространяются на функции точки абстрактного пространства. Можно говорить о дифференцируемости и Д. функции множества по отношению к нек-рой мере.
При выполнении некоторых расчётов в исследованиях, проектировании, анализе полученных опытных путём данных часто возникает необходимость предварительной прикидки результата, которую удобно выполнять, используя дифференциал функции. Приближённые вычисления, выполненные с его помощью, могут дать новые направления дальнейшего изучения объектов и их разработок.
Понятие и геометрический смысл дифференциала
Пусть y = f (x) имеет производную
Применяя свойства предела функции, получают равенство
После умножения обеих частей на приращение аргумента Δx, образуется тождество:
в котором в правой части записано слагаемое, являющееся бесконечно малой одного порядка с Δx, далее идет слагаемое более высокого порядка.
Определение 1
Дифференциалом функции y = f (x) первого порядка называется главная часть её приращения f′(x)Δx, которую обозначают dy (или d(f(x)).
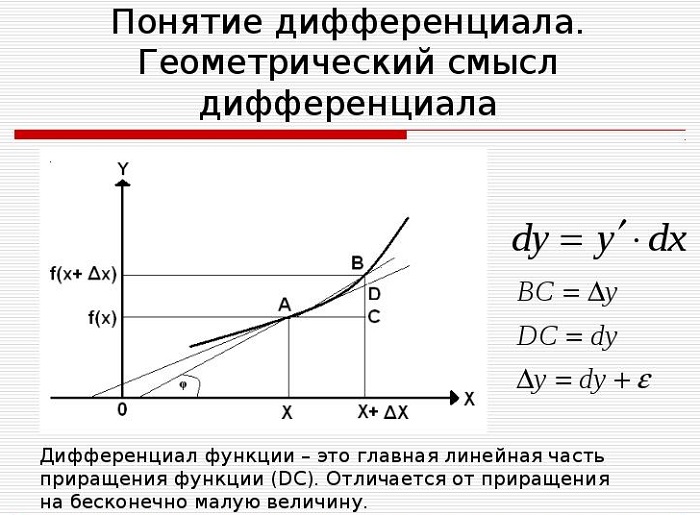
Для наглядного представления и понимания определения рассматривается касательная к графику функции y = f(x) в точке x. Когда значение переменной сдвигается по построенной прямой (получает приращение) на некоторую малую величину Δx, значение второй координаты точки тоже меняется.
Значит, дифференциал функции y = f(x) в точке x равен приращению ординаты касательной, когда её абсцисса меняется на величину Δx.
Определение 2
Дифференциал от дифференциала называется дифференциалом второго порядка. Таким же рекуррентным образом вводятся понятия дифференциалов более высоких порядков.
Формы записи дифференциала
Для нахождения дифференциала независимой переменной рассматривают функцию y = x, учитывая, что x’ = 1, а, следовательно:
Отсюда получается формула:
Для второго порядка вводится обозначение d 2 y.
Свойства дифференциала
Существующая таблица производных помогает выделить некоторые свойства дифференциалов, например, для суммы, произведения, частного получаются следующие правила:
Одним из важных свойств является инвариантность (неизменность) формы записи, независимо от того, является ли функция элементарной или композицией элементарных (сложной). Фактически,
Примеры решения задач
Задача №1
Найти дифференциал функции
Задача №2
Вычислить значение дифференциала функции
В помощь студентам создан онлайн калькулятор, который позволяет ввести функцию, нажать кнопку и получить форму или значение дифференциала.
Если dx есть константа, то для высших порядков имеет место следующая формула:
Этот результат вытекает непосредственно из определения:
Задача №3
Найти d 2 y, если y = cos2x и x – независимая переменная.
Если x – функция от некоторой другой независимой переменной, то свойство инвариантности перестаёт работать, следовательно,
Задача №4
Найти d 2 y, если y = x 2 и x = t 3 + 1, t – независимый аргумент.
Нетрудно заметить, что если выразить y напрямую через t, то получится тот же результат.
с высокой степенью точности можно вычислить приращение любой дифференцируемой зависимости.
Раскрыв Δy, сделав соответствующие преобразования, приходят к формуле приближённых вычислений:
Задача №5
Вычислить приближённо arctg1,05.
Пусть f(x) = arctg x. Тогда
Полный дифференциал функции
Математика не ограничивается множеством функций одного независимого аргумента. Рассматриваются зависимости от двух и более переменных.
Определения похожи, отличается вид главной части. Рассматриваются несколько слагаемых.
Например, если z = f(x;y) то
Последнее равенство есть формула полного дифференциала. Для функции нескольких переменных сохраняется принцип построения.
Если рассматривают приращения только по одной переменной, то приходят к понятию частных дифференциалов.
Заключение
Высшая математика позволяет находить приближённо общий корень системы уравнений, пользуясь дифференциальным исчислением, делать прикидку результатов, прогнозировать получаемое.
Что такое дифференциал матанализ
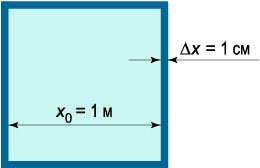
Заметим, что в данном примере коэффициент \(A\) равен значению производной функции \(S\) в точке \(
Коэффициент \(A\) главной части приращения функции в точке \(
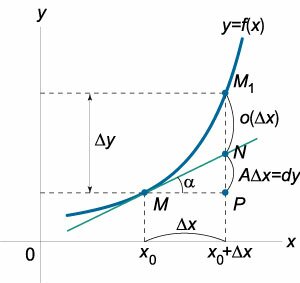
На рисунке \(2\) схематически показана разбивка приращения функции \(\Delta y\) на главную часть \(A\Delta x\) (дифференциал функции) и член высшего порядка малости \(\omicron\left( <\Delta x>\right)\).
Касательная \(MN\), проведенная к кривой функции \(y = f\left( x \right)\) в точке \(M\), как известно, имеет угол наклона \(\alpha\), тангенс которого равен производной: \[\tan \alpha = f’\left( <
Дифференциал (математич.)
функции f ( x ) можно представить в виде
Важную роль в этом обобщении играет понятие линейной функции (линейного отображения). Функция L ( x ) векторного аргумента х называется линейной, если она непрерывна и удовлетворяет равенству
L ( x’ + х» ) = L ( x’ ) + L ( x» )
линейной функции L ( x ) имеет вид
Далее, считая h = h 1 постоянным, можно найти Д. от дифференциала df ( x ; h 1 ) как главную часть приращения
df ( x + h 2 ; h 1 ) ‒ df ( x ; h 1 ),
Всюду выше речь шла об обобщении понятия Д. на числовые функции векторного аргумента. Существует обобщение понятия Д. и на случай вектор-функций, принимающих значения в банаховых пространствах.
Лит.: Ильин В. А., Позняк Э. Г., Основы математического анализа, 2 изд., М., 1967; Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа, 2 изд., М., 1968; Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления, 7 изд., т. 1, М., 1969; Кудрявцев Л. Д., Математический анализ, т. 1, М., 1970; Рудин У., Основы математического анализа, пер. с англ., М., 1966; Дьедонне Ж., Основы современного анализа, пер. с англ., М., 1964.
Полезное
Смотреть что такое «Дифференциал (математич.)» в других словарях:
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ — раздел математики, в к ром изучаются понятия производной и дифференциала и способы их применения к исследованию функций. Развитие Д. и. тесно связано с развитием интегрального исчисления. Неразрывно и их содержание. Вместе они составляют основу… … Математическая энциклопедия
ЛОГИКА ДИАЛЕКТИЧЕСКАЯ — см. в ст. Диалектика. Философский энциклопедический словарь. М.: Советская энциклопедия. Гл. редакция: Л. Ф. Ильичёв, П. Н. Федосеев, С. М. Ковалёв, В. Г. Панов. 1983. ЛОГИКА ДИАЛЕКТИЧЕСКАЯ … Философская энциклопедия
ЗНАКИ МАТЕМАТИЧЕСКИЕ — условные обозначения, предназначенные для записи математич. понятий и выкладок. Напр., понятие квадратный корень из числа, равного отношению длины окружности к ее диаметру обозначается кратко а предложение отношение длины окружности к ее диаметру … Математическая энциклопедия
Бернштейн, Сергей Натанович — (р. 1880) математик, проф. Харьковского ун та, член корреспондент Всесоюзной академии наук, действительный член Украинской акад. наук. По окончании средней школы отправился в Париж, прошел курс математических наук в Сорбонне, провел около 2 лет в … Большая биографическая энциклопедия
ЛЕЙБНИЦ — (Leibniz) Готфрид Вильгельм (1646 1716) нем. философ, математик, физик и изобретатель, юрист, историк, языковед. Изучал юриспруденцию и философию в Лейпцигском и Йенском ун тах. В 1672 1676 в Париже. С 1676 состоял на службе у ганноверских… … Философская энциклопедия
ТЕРМОДИНАМИКИ МАТЕМАТИЧЕСКИЕ ЗАДАЧИ — задачи, связанные с исследованием наиболее общих свойств макроскопич. систем, находящихся в состоянии термодинамич. равновесия, и процессов перехода между этими состояниями. Математич. аппарат макроскопич. термодинамики исходит из т. н. начал… … Математическая энциклопедия
БЕСКОНЕЧНОМЕРНОЕ ПРЕДСТАВЛЕНИЕ — группы Ли представление группы Ли в бесконечномерном векторном пространстве. Теория представлений групп Ли есть часть общей теории, представлений то пологич. групп. Специфика групп Ли позволяет использовать в этой теории средства анализа (в… … Математическая энциклопедия
МАТЕМАТИЧЕСКИЙ АНАЛИЗ — часть математики, в к рой функции и их обобщения изучаются методом пределов. Понятие предела тесно связано с понятием бесконечно малой величины, поэтому можно также сказать, что М. а. изучает функции и их обобщения методом бесконечно малых.… … Математическая энциклопедия
Золотарев, Егор Иванович — известный математик, проф. Петроградского университета, адъюнкт Академии Наук, родился 31 марта 1847 г. в Петрограде, первоначальное образование получил в V Петроградской гимназии. По окончании в ней курса с серебряною медалью З. поступил в 1863… … Большая биографическая энциклопедия