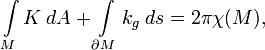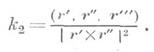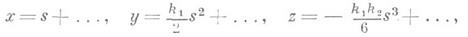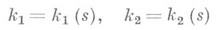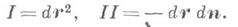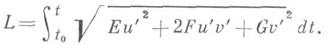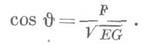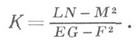Что такое дифференциальная геометрия

Дифференциальная геометрия

Дифференциальная геометрия — это один из разделов геометрии, в котором изучаются свойства кривых, поверхностей и других геометрических многообразий с помощью методов математического анализа, в частности — дифференциального исчисления.

Возникла и развивалась дифференциальная геометрия вместе с математическим анализом, который сам в действительности базируется на геометрии. основные геометрические понятия легли в основу соответствующий терминов анализа. К примеру, понятие площади и объема предшествовало понятию интеграл.

Зародилась дифференциальная геометрия в XVIII веке. Ее появление связано с именами выдающихся математиков того времени Эйлера и Монжа. Первое сводное сочинение по теории поверхностей была написано в 1795 году Монжем «Приложение анализа к геометрии».

В 1827 Гаусс опубликовал работу «Общее исследование о кривых поверхностях», в которой изложил основы теории поверхностей в её современном виде. С этого момента дифференциальная геометрия получила официальный статус самостоятельной отрасли математической науки.

Научно-исследовательские работы по дифференциальной геометрии К. Гаусса (1777-1855гг.), Г. Дарбу (1842-1917гг.), Л. Бианки (1856-1928гг.) и Л.Эйзенхарта (1876-1965гг.) были посвящены, главным образом, свойствам, проявляющимся в малой окрестности обычной точки многообразия. Предмет этих исследований стал сутью так называемой дифференциальной геометрии «в малом». Начиная с 1930-х годов, исследования математиков были направлены, прежде всего, на изучение взаимосвязей между дифференциальной геометрией малых окрестностей и «глобальными» свойствами всего многообразия. Эта теорию получила название дифференциальной геометрией «в целом».

Важную роль в развитии геометрии, и дифференциальной геометрии, в частности, сыграло открытие неевклидовой геометрии. В лекции «О гипотезах, лежащих в основаниях геометрии», прочитанной Риманом в 1854 году, были сформулированы основы новой геометрии. впоследствии эта геометрия стала носить имя своего создателя. Сегодня риманова геометрия является наиболее развитой частью дифференциальной геометрии.

В «Эрлангенской программе» 1872 года Клейн изложил теоретико-групповую точку зрения на геометрию. Согласно Клейну, геометрия — это учение об инвариантах (то есть об неизменных величинах) групп преобразований. Применительно к дифференциальной геометрии это учение было развито Картаном, который создал теорию пространственно-проективной и аффинной (родственной) связности.

Следует отметить, что дифференциальная геометрия и топология являются смежными разделами математики. Однако топология значительно более молодой раздел, который начал развиваться лишь в начале XX века.

Наиболее фундаментальная из известных взаимосвязей между топологией и дифференциальной геометрией устанавливается теоремой Гаусса — Бонне, которая утверждает, что для обычных замкнутых поверхностей

Надо сказать, что дифференциальная геометрия также как и вся геометрия подразделяется на несколько основных отраслей. К ним относятся:

Первоначально дифференциальная геометрия занималась изучением свойств кривых поверхностей в обычном пространстве, в настоящее время в область ее изучения вошли многообразия любого числа измерений, которые могут быть, а могут и не быть подпространствами евклидова пространства.

Источник

ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ

— раздел геометрии, в к-ром изучаются геометрич. образы, в первую очередь кривые и поверхности, методами математич. анализа. Обычно в Д. г. изучаются свойства кривых и поверхностей в малом, т. е. свойства сколь угодно малых их кусков. Кроме того, в Д. г. изучаются свойства семейств линий и поверхностей (см., напр., Конгруэнция, Сеть).

Возникновение Д. г. относится к 18 в. и связано с именами Л. Эйлера (L. Euler) и Г. Монжа (G. Monge). Первое сводное сочинение по теории поверхностей написано Г. Монжем (Приложение анализа к геометрии, 1795). В 1827 К. Гаусс (С. Gauss) опубликовал работу «Общее исследование о кривых поверхностях», в к-рой заложил основы теории поверхностей в ее современном виде. С тех пор Д. г. перестала быть только приложением анализа и заняла самостоятельное место в математике.

Открытие в 1826 Н. И. Лобачевским неевклидовой геометрии сыграло огромную роль в развитии всей геометрии, в том. 1, если при где д(Х)- расстояние точки Xмножества Мот т. Если в качестве Мвзять кривую, а в качестве тпрямую, проходящую через точку Окривой, то при условие соприкосновения определяет касательную к кривой в точке О(рис. 1).

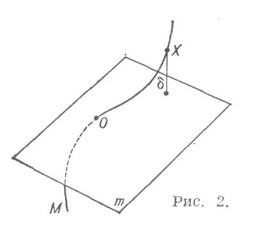
Гладкая (дифференцируемая) кривая в каждой точке имеет определенную касательную. Направление касательной в точке t₀ кривой, задаваемой уравнениями (1), совпадает с направлением вектора [ х’(t₀), у’(t₀), z(t₀)]. В Д. г. выводятся уравнения касательной для различных способов аналитич. адания кривой. В частности, для кривой, задаваемой уравнениями (1), уравнения касательной в точке, отвечающей значению параметра t₀, будут

где индекс ₀ указывает на значение функций х, у, z и их производных в точке t₀. Если взять в качестве тплоскость, проходящую через точку Окривой М, то условие соприкосновения при определяет соприкасающуюся плоскость кривой (рис. 2).

Дважды дифференцируемая кривая в каждой точке имеет соприкасающуюся плоскость. Она либо единственная, либо любая плоскость, проходящая череа касательную кривой, является соприкасающейся.

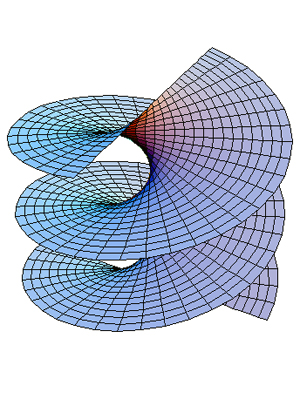
При движения вдоль кривой ее касательная вращается. Скорость этого вращения при равномерном, с единичной скоростью, движении вдоль кривой наз. кривизной кривой. В случае параметрич. задания кривой уравнениями (1) кривизна кривой определяется по формуле где r(t)- вектор-функция с координатами x(t), y(t), z). Прямые и только прямые имеют всюду равную нулю кривизну. Дважды дифференцируемая кривая в каждой точке, где кривизна отлична от нуля, имеет единственную соприкасающуюся плоскость. При движении вдоль кривой в окрестности такой точки соприкасающаяся плоскость вращается, причем касательная кривой является мгновенной осью этого вращения. Скорость вращения соприкасающейся плоскости при равномерном, с единичной скоростью, движении вдоль кривой наз. кручением кривой. В зависимости от направления вращения определяется знак кручения. Трижды дифференцируемая кривая в каждой точке с отличной от нуля кривизной имеет определенное кручение. В случае параметрич. задания кривой уравнениями (1) кручение кривой определяется по формуле

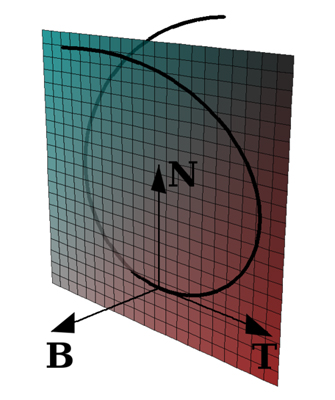
Прямая, перпендикулярная касательной, проходящая через точку касания, наз. нормалью к кривой. Нормаль, лежащую в соприкасающейся плоскости, наз. главной нормалью, а нормаль, перпендикулярную соприкасающейся плоскости, наз. бинормалью. Фигура, составленная из касательной, главной нормали и бинормали, а также из трех плоскостей, попарно содержащих эти прямые, наз. естественным трехгранником (трехгранником Френе). Если ребра естественного трехгранника в данной точке кривой принять за оси прямоугольной декартовой системы координат, то уравнение кривой в естественной параметризации имеет в окрестности этой точки вид

где k₁ и k₂ — кривизна и кручение кривой в указанной точке. На рис. 3 изображены проекции кривой на грани естественного трехгранника вблизи точки с отличными от нуля кривизной и кручением.

Единичные векторы t, v, b касательной, главной нормали и бинормали кривой при движении вдоль кривой изменяются. При соответствующем выборе направления этих векторов из определения кривизны и кручения получаются формулы

где штрихом обозначено дифференцирование по дуге кривой. Формулы (2) наз. Френе формулами. Кривая с отличной от нуля кривизной определяется с точностью до положения в пространстве заданием ее кривизны и кручения в функции дуги sкривой. В связи с этим систему уравнений

наз. натуральными уравнениями кривой.

Важный класс кривых представляют плоские кривые, т. 2 с поверхностью в этой точке. В каждой точке дважды дифференцируемой поверхности существует единственный соприкасающийся параболоид, к-рый может вырождаться в параболич. цилиндр или плоскость. 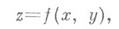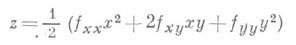Если поверхность отнести к прямоугольным декартовым координатам, приняв данную точку поверхности за начало координат, а касательную плоскость в ней за плоскость ху, то уравнение поверхности в окрестности точки касания будет а уравнение соприкасающегося параболоида в этой точке (производные функции f берутся в точке касания). В зависимости от вида соприкасающегося параболоида точки поверхности подразделяются на эллиптические точки, гиперболические точки, параболические точки и уплощения точки. Значение соприкасающегося параболоида состоит в том, что он воспроизводит форму поверхности с точностью до бесконечно малых 2-го порядка (касательная плоскость воспроизводит ее форму с точностью до бесконечно малых 1-го порядка).

С помощью соприкасающегося параболоида вводится понятие сопряженных направлений на поверхности. Именно два направления на поверхности в данной точке наз. сопряженными, если содержащие их прямые сопряжены относительно соприкасающегося параболоида в этой точке. Ортогональные сопряженные направления наз. главными. В данной точке поверхности, как правило, два главных направления. Исключение составляют точки уплощения и специальные эллиптич. течки ( округления точки), в к-рых каждое направление главное. Линия, у к-рой в каждой точке направление является главным, наз. кривизны линией. В точках поверхности, не являющихся эллиптическими, существуют самосопряженные направления. Они наз. асимптотическими направлениями. Линия на поверхности, направление к-рой в каждой точке асимптотическое, наз. асимптотической линией.

Подобно тому, как для семейства кривых на плоскости, вводится понятие огибающей семейства поверхностей. При этом семейство поверхностей может быть однопараметрическим или двухпараметрическим. В теории поверхностей особое значение имеет огибающая однопараметрич. семейства плоскостей.

В теории поверхностей важную роль играют две дифференциальные квадратичные формы поверхности, связанные с поверхностью. Если через r(u, v )обозначить вектор точки на поверхности, а через ( и, v )единичный вектор нормали к поверхности, то эти квадратичные формы записываются в виде

Коэффициенты первой и второй квадратичных форм обычно обозначаются Е, 2F, G и L, 2M, N соответственно. Первая из этих форм дает расстояние на поверхности между точкой (и, v)и бесконечно близкой точкой (u+du,u+du):

Длина кривой, задаваемой на поверхности уравнениями u=u(t), v=v(t), вычисляется при помощи первой квадратичной формы

Первая квадратичная форма, поверхности определяет углы между кривыми на поверхности. В частности, для угла J между координатными линиями u=const, u=const в точке их пересечения имеет место формула

Отсюда видно, что координатная сеть на поверхности ортогональна, если F=0. Площадь поверхности также определяется первой квадратичной формой и для области W на поверхности вычисляется по формуле

Вторая квадратичная форма характеризует искривленность поверхности в пространстве. Именно, отношение второй квадратичной формы к первой

представляет собой кривизну плоского сечения, нормального к поверхности, проведенного в направлении du: dv (см. Нормальная кривизна поверхности). Существует простая связь между кривизной кривой, лежащей на поверхности, и кривизной нормального сечения поверхности, проведенного через касательную кривой ( Менъе теорема). Экстремальные значения нормальной кривизны поверхности в данной точке наз. главными кривизнами. Они достигаются по главным направлениям. Нормальная кривизна поверхности в произвольном направлении выражается через главные кривизны и углы, к-рые это направление образует с главными (Эйлера формула). Главные кривизны k₁ и k₂ определяются из уравнения

Из этой формулы видно, что гауссова кривизна поверхности выражается через коэффициенты первой и второй квадратичных форм. Однако гауссову кривизну можно выразить через коэффициенты только первой формы и их производные (Гаусса теорема).

Две поверхности, между к-рыми может быть установлен гомеоморфизм, сохраняющий длины кривых, наз. изометричными поверхностями.

Коэффициенты первой и второй квадратичных форм независимы. Одно из соотношений между этими коэффициентами дает теорема Гаусса. Существуют еще два соотношения, открытые К. М. Петерсоном и Д. Кодацци (D. Codazzi) (см. Петерсона— Кодацци уравнения). Эти три соотношения составляют полную систему независимых соотношений между коэффициентами первой и второй квадратичных форм поверхности. Согласно Бонне теореме, если для двух дифференциальных квадратичных форм, из к-рых первая положительно определенная, выполнены соотношения Гаусса, Петерсона, Кодацци, то существует, и притом единственная, с точностью до положения в пространстве, поверхность, имеющая эти формы первой и соответственно второй квадратичными формами.

Источник

Дифференциальная геометрия

Дифференциа́льная геоме́трия и дифференциальная тополо́гия — два смежных раздела математики, которые изучают гладкие многообразия (обычно с дополнительными структурами). Эти два раздела математики почти неразделимы. Они находят множество применений в физике, особенно в общей теории относительности.

Различие между этими науками состоит в наличии или отсутствии локальных инвариантов. В дифференциальной топологии рассматриваются такие структуры на многообразиях, что у любой пары точек можно найти идентичные окрестности, тогда как в дифференциальной геометрии присутствуют локальные инварианты (кривизна) которые делают точки локально отличимыми.

История

Дифференциальная геометрия возникла и развивалась в тесной связи с математическим анализом, который сам в значительной степени вырос из задач геометрии. Многие геометрические понятия предшествовали соответствующим понятиям анализа. Так, например, понятие касательной предшествовало понятию производной, понятие площади и объема — понятию интеграла.

Возникновение дифференциальной геометрии относится к XVIII веку и связано с именами Эйлера и Монжа. Первое сводное сочинение по теории поверхностей написано Монжем («Приложение анализа к геометрии», 1795). В 1827 Гаусс опубликовал работу «Общее исследование о кривых поверхностях», в которой заложил основы теории поверхностей в её современном виде. С тех пор дифференциальная геометрия перестала быть только приложением анализа и заняла самостоятельное место в математике.

Огромную роль в развитии всей геометрии, в том числе и дифференциальной геометрии, сыграло открытие неевклидовой геометрии. Риман в своей лекции «О гипотезах, лежащих в основаниях геометрии» (1854) заложил основы римановой геометрии, наиболее развитой части современной дифференциальной геометрии.

Теоретико-групповая точка зрения Клейна, изложенная в его «Эрлангенской программе» (1872), то есть: геометрия — учение об инвариантах групп преобразований, в применении к дифференциальной геометрии была развита Картаном, который построил теорию пространств проективной связности и аффинной связности.

Дифференциальная топология является гораздо более молодым разделом математики, он начинает развиваться только в начале XX века.

Основные подразделы дифференциальной геометрии и топологии

Литература

Полезное

Смотреть что такое «Дифференциальная геометрия» в других словарях:

ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ — раздел геометрии, в которой геометрические образы изучаются на основе метода координат средствами дифференциального исчисления. Первоначально предметом дифференциальной геометрии было изучение геометрических образов обычного трехмерного… … Большой Энциклопедический словарь

ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ — ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ, тип геометрии, в которой используются методы дифференциального ИСЧИСЛЕНИЯ для анализа геометрических понятий, таких как кривые и поверхности. Например, кривую, описывающую траекторию полета снаряда либо орбиту… … Научно-технический энциклопедический словарь

Дифференциальная геометрия — раздел геометрии, в котором геометрические образы изучаются методами математического анализа. Главными объектами Д. г. являются произвольные достаточно гладкие кривые (линии) и поверхности евклидова пространства, а также семейства линий и … Большая советская энциклопедия

ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ — раздел геометрии, в к ром изучаются геометрич. образы, в первую очередь кривые и поверхности, методами математич. анализа. Обычно в Д. г. изучаются свойства кривых и поверхностей в малом, т. е. свойства сколь угодно малых их кусков. Кроме того, в … Математическая энциклопедия

ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ — раздел геометрии, в котором свойства кривых, поверхностей и других геометрических многообразий изучаются методами математического анализа, в первую очередь дифференциального исчисления. Работы по дифференциальной геометрии К. Гаусса (1777 1855),… … Энциклопедия Кольера

дифференциальная геометрия — раздел геометрии, в которой геометрические образы изучаются на основе метода координат средствами дифференциального исчисления. Первоначально предметом дифференциальной геометрии было изучение геометрических образов обычного трёхмерного… … Энциклопедический словарь

ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ — часть геометрии, изучающая геом. образы на основе метода координат средствами дифференц. исчисления. Первоначально Д. г. изучала геом. образы обычного 3 мерного пространства (линии, поверхности), а затем (со 2 й пол. 19 в.) и многомерных… … Большой энциклопедический политехнический словарь

ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ — раздел геометрии, в к рой геом. образы изучаются на основе метода координат средствами дифференц. исчисления. Первонач. предметом Д. г. было изучение геом. образов обычного трёхмерного пространства (линий, поверхностей). Со 2 й пол. 19 в. рамки Д … Естествознание. Энциклопедический словарь

Дифференциальная геометрия кривых — раздел дифференциальной геометрии, который занимается исследованием гладких пространственных и плоских кривых в евклидовом пространстве аналитическими методами. Содержание 1 Способы задания кривой 1.1 Плоские кривые … Википедия

Дифференциальная геометрия и топология — Дифференциальная геометрия и дифференциальная топология два смежных раздела математики, которые изучают гладкие многообразия (обычно с дополнительными структурами). Эти два раздела математики почти неразделимы, при этом часто оба раздела… … Википедия

Источник

Что такое дифференциальная геометрия

Тогда единичный вектор касательной к кривой задается формулой

Вектор dT/ds в каждой точке кривой перпендикулярен к касательной, а его длина равна кривизне k кривой. Прямая, перпендикулярная касательной, проходящая через точку касания, называется нормалью к кривой. Следовательно, если N – единичный вектор нормали, то

Кроме того, можно показать, что

Полезно также ввести величины g ij :

Первая фундаментальная форма полностью определяет внутреннюю геометрию поверхности, т.е. ту геометрию, которую наблюдал бы воображаемый обитатель поверхности, неспособный воспринимать происходящие вне нее явления. Такое двумерное существо находилось бы в положении, сравнимом с положением обычного трехмерного человека, воспринимающего геометрию нашего трехмерного пространства, но неспособного воспринимать свойства пространства большего числа измерений, в котором лежит наше пространство (если такое пространство действительно существует).

Величины Г i _jk в (9) называются символами Кристоффеля второго рода. Они определяются через величины [ i, j, k] (символы Кристоффеля первого рода) соотношениями

где по определению

Величины b _ij в (9) называются коэффициентами второй основной формы поверхности. Сравнивая (9) с (5), нетрудно видеть, что для поверхности b_ij играют такую же роль, как кривизна для плоских кривых: они описывают внешние свойства поверхности – непостижимые для воображаемого двумерного существа, живущего на поверхности, но доступные пониманию обычного трехмерного человека.

Любой единичный вектор, касательный к поверхности, может быть записан в виде

где g ₁₁ l 1 l 1 + 2 g ₁₂ l 1 l 2 + g ₂₂ l 2 l 2 = 1. Кривизна поверхности в направлении вектора l равна

Важную роль играют поверхности с постоянной гауссовой кривизной. При K = 0 поверхность плоская, или развертывающаяся, поскольку у нее такая же внутренняя геометрия, как у плоскости. Примерами развертывающихся поверхностей могут служить прямые круговые конусы и цилиндры. При K > 0 поверхность имеет эллиптическую неевклидову геометрию, а при K 0 – гиперболическую неевклидову геометрию.

Величина ( R _lijk ) называется тензором кривизны поверхности.

Секционная кривизна K ₁₂ риманова пространства в точке P определяется через ориентацию, задаваемую двумя векторами l ₁ и l ₂ :

Свернутый тензор кривизны, определяемый выражением

где интеграл берется по всей поверхности, K – гауссова кривизна и c – характеристика Эйлера – Пуанкаре. На произвольные замкнутые римановы пространства этот результат был распространен в 1943 К.Аллендёрфером и А.Вейлем. См. также МАТЕМАТИЧЕСКИЙ АНАЛИЗ; ТОПОЛОГИЯ.

Источник

дифференциальная геометрия

Смотреть что такое «дифференциальная геометрия» в других словарях:

ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ — раздел геометрии, в которой геометрические образы изучаются на основе метода координат средствами дифференциального исчисления. Первоначально предметом дифференциальной геометрии было изучение геометрических образов обычного трехмерного… … Большой Энциклопедический словарь

ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ — ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ, тип геометрии, в которой используются методы дифференциального ИСЧИСЛЕНИЯ для анализа геометрических понятий, таких как кривые и поверхности. Например, кривую, описывающую траекторию полета снаряда либо орбиту… … Научно-технический энциклопедический словарь

Дифференциальная геометрия — раздел геометрии, в котором геометрические образы изучаются методами математического анализа. Главными объектами Д. г. являются произвольные достаточно гладкие кривые (линии) и поверхности евклидова пространства, а также семейства линий и … Большая советская энциклопедия

Дифференциальная геометрия — и дифференциальная топология два смежных раздела математики, которые изучают гладкие многообразия (обычно с дополнительными структурами). Эти два раздела математики почти неразделимы. Они находят множество применений в физике, особенно в общей… … Википедия

ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ — раздел геометрии, в к ром изучаются геометрич. образы, в первую очередь кривые и поверхности, методами математич. анализа. Обычно в Д. г. изучаются свойства кривых и поверхностей в малом, т. е. свойства сколь угодно малых их кусков. Кроме того, в … Математическая энциклопедия

ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ — раздел геометрии, в котором свойства кривых, поверхностей и других геометрических многообразий изучаются методами математического анализа, в первую очередь дифференциального исчисления. Работы по дифференциальной геометрии К. Гаусса (1777 1855),… … Энциклопедия Кольера

ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ — часть геометрии, изучающая геом. образы на основе метода координат средствами дифференц. исчисления. Первоначально Д. г. изучала геом. образы обычного 3 мерного пространства (линии, поверхности), а затем (со 2 й пол. 19 в.) и многомерных… … Большой энциклопедический политехнический словарь

ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ — раздел геометрии, в к рой геом. образы изучаются на основе метода координат средствами дифференц. исчисления. Первонач. предметом Д. г. было изучение геом. образов обычного трёхмерного пространства (линий, поверхностей). Со 2 й пол. 19 в. рамки Д … Естествознание. Энциклопедический словарь

Дифференциальная геометрия кривых — раздел дифференциальной геометрии, который занимается исследованием гладких пространственных и плоских кривых в евклидовом пространстве аналитическими методами. Содержание 1 Способы задания кривой 1.1 Плоские кривые … Википедия

Дифференциальная геометрия и топология — Дифференциальная геометрия и дифференциальная топология два смежных раздела математики, которые изучают гладкие многообразия (обычно с дополнительными структурами). Эти два раздела математики почти неразделимы, при этом часто оба раздела… … Википедия

Источник