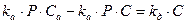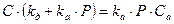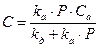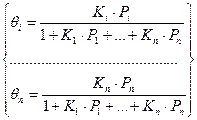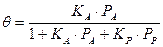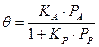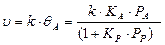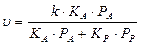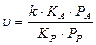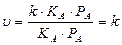Что такое диффузия в химии

Диффузия

Из Википедии — свободной энциклопедии

Примером диффузии может служить перемешивание газов (например, распространение запахов) или жидкостей (если в воду капнуть чернил, то жидкость через некоторое время станет равномерно окрашенной). Другой пример связан с твёрдым телом: атомы соприкасающихся металлов перемешиваются на границе соприкосновения.

Скорость протекания диффузии зависит от многих факторов. Так, в случае металлического стержня тепловая диффузия проходит с огромной скоростью. Если же стержень изготовлен из материала с низкой теплопроводностью (например, стекла), тепловая диффузия протекает медленно. Диффузия молекул в общем случае протекает ещё медленнее. Например, если кусочек сахара опустить на дно стакана с водой и воду не перемешивать, то пройдёт несколько недель, прежде чем раствор станет однородным. Ещё медленнее происходит диффузия одного твёрдого вещества в другое. Например, Роберт Бойль показал, что если медь покрыть золотом, то будет происходить диффузия золота в медь. При этом при нормальных условиях (комнатная температура и атмосферное давление) золотосодержащий слой достигнет толщины в несколько микронов только через несколько тысяч лет. [3] Другой пример — систематические исследования диффузии свинца в золото, проведенные Уильямом Робертсом-Остеном и опубликованные в 1896 г. Под грузом за пять лет свинцовый слиток проник в золотой слиток на один миллиметр. [4]

Первое систематическое экспериментальное исследование диффузии было выполнено Томасом Грэмом. Он изучал диффузию в газах, и это явление (Закон Грэма) было описано им в 1831—1833 гг. [5]

Большой вклад в теорию и практику исследования дифузионных процессов внес Я. И. Френкель, предложив и развив в 1926 году идею диффузии локальных дефектов (вакансий и межузельных атомов). [7]

Источник

Диффузия

Примером диффузии может служить перемешивание газов (например, распространение запахов) или жидкостей (если в воду капнуть чернил, то жидкость через некоторое время станет равномерно окрашенной). Другой пример связан с твёрдым телом: атомы соприкасающихся металлов перемешиваются на границе соприкосновения. Важную роль диффузия частиц играет в физике плазмы.

Обычно под диффузией понимают процессы, сопровождающиеся переносом материи, однако иногда диффузионными называют также другие процессы переноса: теплопроводность, вязкое трение и т. п.

Скорость протекания диффузии зависит от многих факторов. Так, в случае металлического стержня тепловая диффузия проходит очень быстро. Если же стержень изготовлен из синтетического материала, тепловая диффузия протекает медленно. Диффузия молекул в общем случае протекает ещё медленнее. Например, если кусочек сахара опустить на дно стакана с водой и воду не перемешивать, то пройдёт несколько недель, прежде чем раствор станет однородным. Ещё медленнее происходит диффузия одного твёрдого вещества в другое. Например, если медь покрыть золотом, то будет происходить диффузия золота в медь, но при нормальных условиях (комнатная температура и атмосферное давление) золотосодержащий слой достигнет толщины в несколько микронов только через несколько тысяч лет.

Количественно описание процессов диффузии было дано немецким физиологом А. Фиком (англ.) в 1855 г.

Содержание

Общее описание

Все виды диффузии подчиняются одинаковым законам. Скорость диффузии пропорциональна площади поперечного сечения образца, а также разности концентраций, температур или зарядов (в случае относительно небольших величин этих параметров). Так, тепло будет в четыре раза быстрее распространяться через стержень диаметром в два сантиметра, чем через стержень диаметром в один сантиметр. Это тепло будет распространяться быстрее, если перепад температур на одном сантиметре будет 10 °C вместо 5 °C. Скорость диффузии пропорциональна также параметру, характеризующему конкретный материал. В случае тепловой диффузии этот параметр называется теплопроводность, в случае потока электрических зарядов — электропроводность. Количество вещества, которое диффундирует в течение определённого времени, и расстояние, проходимое диффундирующим веществом, пропорциональны квадратному корню времени диффузии.

Диффузия представляет собой процесс на молекулярном уровне и определяется случайным характером движения отдельных молекул. Скорость диффузии в связи с этим пропорциональна средней скорости молекул. В случае газов средняя скорость малых молекул больше, а именно она обратно пропорциональна квадратному корню из массы молекулы и растёт с повышением температуры. Диффузионные процессы в твёрдых телах при высоких температурах часто находят практическое применение. Например, в определённых типах электронно-лучевых трубок (ЭЛТ) применяется металлический торий, продиффундировавший через металлический вольфрам при 2000 °C.

Если в смеси газов масса одной молекулы в четыре раза больше другой, то такая молекула передвигается в два раза медленнее по сравнению с её движением в чистом газе. Соответственно, скорость диффузии её также ниже. Эта разница в скорости диффузии лёгких и тяжёлых молекул применяется, чтобы разделять субстанции с различными молекулярными весами. В качестве примера можно привести разделение изотопов. Если газ, содержащий два изотопа, пропускать через пористую мембрану, более лёгкие изотопы проникают через мембрану быстрее, чем тяжёлые. Для лучшего разделения процесс производится в несколько этапов. Этот процесс широко применялся для разделения изотопов урана (отделение 235 U от основной массы 238 U). Поскольку такой способ разделения требует больших энергетических затрат, были развиты другие, более экономичные способы разделения. Например, широко развито применение термодиффузии в газовой среде. Газ, содержащий смесь изотопов, помещается в камеру, в которой поддерживается пространственный перепад (градиент) температур. При этом тяжёлые изотопы со временем концентрируются в холодной области.

Уравнения Фика

С точки зрения термодинамики движущим потенциалом любого выравнивающего процесса является рост энтропии. При постоянных давлении и температуре в роли такого потенциала выступает химический потенциал µ, обуславливающий поддержание потоков вещества. Поток частиц вещества пропорционален при этом градиенту потенциала

В большинстве практических случаев вместо химического потенциала применяется концентрация C. Прямая замена µ на C становится некорректной в случае больших концентраций, так как химический потенциал перестаёт быть связан с концентрацией по логарифмическому закону. Если не рассматривать такие случаи, то вышеприведённую формулу можно заменить на следующую:

которая показывает, что плотность потока вещества J [] пропорциональна коэффициенту диффузии D [()] и градиенту концентрации. Это уравнение выражает первый закон Фика. Второй закон Фика связывает пространственное и временное изменения концентрации (уравнение диффузии):

Коэффициент диффузии D зависит от температуры. В ряде случаев в широком интервале температур эта зависимость представляет собой уравнение Аррениуса.

Дополнительное поле, наложенное параллельно градиенту химического потенциала, нарушает стационарное состояние. В этом случае диффузионные процессы описываются нелинейным уравнением Фоккера—Планка. Процессы диффузии имеют большое значение в природе:

Геометрическое описание уравнения Фика

Во втором уравнении Фика в левой части стоит скорость изменения концентрации во времени, а в правой части уравнения — вторая частная производная, которая выражает пространственное распределение концентрации, в частности, выпуклость функции распределения температур, проецируемую на ось х.

Источник

Рассмотрим две системы; S₁ и S₂ в то же температура и способен обменивать частицы. Если есть изменение в потенциальная энергия системы; например μ₁> μ₂ (μ есть Химический потенциал) энергия поток будет происходить из S₁ к S₂, потому что природа всегда предпочитает низкую энергию и максимум энтропия.

Молекулярная диффузия обычно описывается математически с использованием Законы диффузии Фика.

Содержание

Приложения

Диффузия имеет фундаментальное значение во многих дисциплинах физики, химии и биологии. Некоторые примеры применения диффузии:

Значимость

Распространение является частью явления переноса. Из механизмов массопереноса молекулярная диффузия известна как более медленная.

Биология

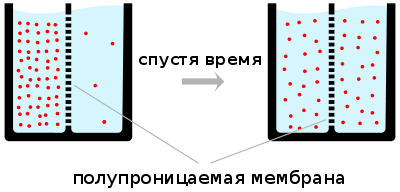
В клеточная биология, диффузия является основным способом транспортировки необходимых материалов, таких как аминокислоты внутри клеток. [1] Распространение растворителей, например воды, через полупроницаемая мембрана классифицируется как осмос.

Метаболизм и дыхание частично полагаются на диффузию в дополнение к объемным или активным процессам. Например, в альвеолы из млекопитающее легкиеиз-за различий в парциальных давлениях на альвеолярно-капиллярной мембране, кислород проникает в кровь и углекислый газ рассеивается. Легкие имеют большую площадь поверхности, что способствует процессу газообмена.

Индикатор, самодиффузия и химическая диффузия

Принципиально различают два типа диффузии:

В коэффициенты диффузии для этих двух типов диффузии, как правило, различаются, потому что коэффициент диффузии для химической диффузии бинарный и включает эффекты, обусловленные корреляцией движения различных диффундирующих частиц.

Неравновесная система

Неравновесные жидкостные системы можно успешно моделировать с помощью флуктуирующей гидродинамики Ландау-Лифшица. В этой теоретической схеме диффузия обусловлена ​​флуктуациями, размеры которых варьируются от молекулярного до макроскопического масштаба. [3]

Зависимая от концентрации «коллективная» диффузия

Коллективная диффузия представляет собой диффузию большого количества частиц, чаще всего внутри растворитель.

Вопреки Броуновское движение, которая представляет собой диффузию отдельной частицы, взаимодействия между частицами могут быть рассмотрены, если только частицы не образуют идеальную смесь со своим растворителем (условия идеальной смеси соответствуют случаю, когда взаимодействия между растворителем и частицами идентичны взаимодействиям между частицами и взаимодействием между молекулами растворителя; в этом случае частицы не взаимодействуют внутри растворителя).

В случае идеальной смеси частица уравнение диффузии справедливо и коэффициент диффузии D скорость распространение в уравнении диффузии частиц не зависит от концентрации частиц. В других случаях возникающие в результате взаимодействия между частицами в растворителе будут учитывать следующие эффекты:

Молекулярная диффузия газов

Это основное уравнение применимо к ряду ситуаций. Ограничение обсуждения исключительно условиями устойчивого состояния, в которых ни dC_А/ dx или dC_B/ dx изменяется во времени, сначала рассматривается эквимолекулярная контрдиффузия.

Эквимолекулярная контрдиффузия

Парциальное давление A изменяется на dP_А на расстоянии dx. Аналогично парциальное давление B изменяет dP_B. Поскольку нет никакой разницы в общем давлении через элемент (нет объемного потока), мы имеем

Для идеального газа парциальное давление связано с молярной концентрацией соотношением

где n_А это количество молей газа А в томе V. Поскольку молярная концентрация C_А равно п_А/ V следовательно

Следовательно, для газа А

Аналогичное уравнение можно вывести для встречной диффузии газа B.

Источник

Диффузия

Диффузией называется самопроизвольный процесс перемещения вещества в растворе, приводящий к выравниванию его концентрации.

В ходе диффузии некоторая первоначальная упорядоченность в распределении вещества (высокая концентрация вещества в одной части системы и низкая – в другой) сменяется полной беспорядоченностью распределения вещества в объеме, при этом энтропия системы возрастает. Когда концентрация раствора во всем объеме выравнивается, энтропия достигает максимального значения, и диффузия прекращается. Скорость диффузии при постоянных температуре и вязкости среды зависит от величины и формы растворяющихся частиц.

Диффузия наблюдается как в жидкостях и газах, так и в твердых веществах. Мерой диффузии является масса вещества 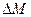, продиффундировавшего за единицу времени через единицу площади поверхности соприкасающихся веществ. Величина тем больше, чем больше изменяется концентрация на единицу длины вдоль направления, в котором происходит диффузия. Скорость диффузии увеличивается с ростом температуры, что связано с увеличением скорости движения частиц.

При гетерогенном катализе химическая реакция протекает на поверхности твердого тела, поэтому процессы транспорта веществ к поверхности и от нее играют важную роль. Если химическое превращение идет гораздо медленнее процессов массообмена, то кинетика реакции определяется процессами на поверхности твердого тела. Если реакция очень быстрая, то кинетика зависит от процессов массообмена.

Рассмотрим диффузию вещества из объема на поверхность реагирующих веществ или на поверхность катализатора, если таковой имеется. Пусть превращение вещества – реакция первого порядка со скоростью, равной

(46)

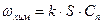
где ω_хим – количество вещества, реагирующего у поверхности S в единицу времени, С_п – концентрация реагента у поверхности.

Всю реагирующую смесь можно разделить на две области:

1. область постоянной концентрации вдали от поверхности реакции;

2. область быстрого изменения концентрации непосредственно вблизи этой поверхности.

Экспериментально установлено, что на всех твердых поверхностях, с которыми граничит движущаяся жидкость, скорость движения жидкости равна нулю. Транспорт вещества происходит через неподвижный слой жидкости, прилегающий к поверхности твердого тела, в результате диффузии реагирующих веществ. Этот неподвижный слой называется слоем Нернста, его толщина зависит от свойств растворителя и растворенного вещества, скорости перемещения и т.д. Например, для жидкости толщина этого слоя δ составляет примерно 0.02 – 0.05 мм и меньше. За его пределами движение жидкости приводит к выравниванию концентрации в объеме раствора. Перенос массы в результате диффузии описывается уравнением Фика:

(47)

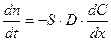
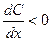
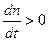
где dn/dt – количество вещества, диффундирующего за единицу времени через фиксированную поверхность S в сторону возрастающих значений x; x – направление диффузии; D – коэффициент диффузии; знак «-» означает, что поток вещества идет в направлении убыли концентрации, поэтому для всегда .

Существует и другая запись уравнения диффузии при Т = Const:

(48)

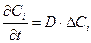
Градиент концентрации (gradC) в диффузионном слое постоянен, поэтому выражение (47) можно записать следующим образом:

(49)

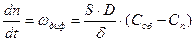
Когда в установившемся стационарном режиме скорость подвода вещества к реагирующей поверхности равна скорости химической реакции, поверхностную концентрацию можно представить как:

(50)

(51)

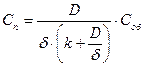
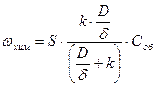
Для быстрой реакции, когда k>>D/d скорость процесса определяется диффузией. В случае медленной реакции, когда k

Моделирование гетерогенно-каталитических реакций.

Обычно гетерогенно-каталитические процессы протекают в жидкой, газовой или паровой фазе при участии твердого катализатора. В случае газовой гетерогенно-каталитической реакции исходные реагенты и продукты реакции являются газами. При их участии в реакции каждая молекула реагента последовательно проходит следующие стадии процесса:

— диффузионный перенос из газовой среды к поверхности катализатора;

— адсорбцию на его поверхности;

— химическое превращение в адсорбированном слое;

— десорбцию продуктов реакции;

— диффузионный перенос продуктов реакции от поверхности катализатора в газовую фазу.

На скорость гетерогенно-каталитической реакции боль­шое влияние оказывает площадь активной поверхности твердого катализатора. Для ее увеличения катализаторы обычно выполняют в виде зерен с сильно развитой поверхностью. При этом кажущаяся поверхность зерен ничтожна по сравнению с поверхностью внутренних пор и каналов в зерне. Значения длины и диаметра внутренних каналов и пор должны исключать сильное торможение диффузионно-транспортных стадий процесса. Наиболее выгоден режим, при котором лимитирующей стадией процесса является собственно химическое превращение. В этом случае говорят, что процесс идет в кинетической области, однако, не всегда удается устранить диффузионное торможение.

Обычно скорость химической реакции определяется по уравнению (47). Если гетерогенная каталитическая реакция является многокомпонентной, кинетическая формула может оказаться достаточно громоздкой. Рассмотрим кинетические уравнения, выведенные из предположения об ограниченной активности поверхности катализатора. Предполагается, что химическое превращение может происходить только на участках молекул, попавших за счет адсорбции на активный центр катализатора.

Сорбцией называется любой процесс поглощения одного вещества другим независимо от механизма поглощения. В зависимости от механизма сорбции различают:

— адсорбцию – изменение концентрации вещества на границе раздела фаз. Адсорбция происходит на любых межфазовых поверхностях, и адсорбироваться могут любые вещества. Адсорбционное равновесие, т.е. равновесное распределение вещества между пограничным слоем и граничащими фазами, является динамическим равновесием и быстро устанавливается. Адсорбция с повышением температуры уменьшается;

— абсорбцию – поглощение одного вещества другим происходит во всем объеме сорбента (например, растворение газа в жидкостях);

— хемосорбцию – поглощение одного вещества другим сопровождается химическими реакциями;

— капиллярную конденсацию – происходящую вследствие того, что давление паров над вогнутым мениском жидкости в смачиваемых ею узких капиллярах меньше давления насыщенного пара над плоской поверхностью жидкости при той же температуре.

Положительная адсорбция, приводящая к повышению концентрации вещества в пограничном слое, возможна только при уменьшении величины поверхностного натяжения, т.е. все самопроизвольные процессы на границе раздела фаз происходят в направлениях уменьшения свободной поверхностной энергии.

Статическая сорбция наблюдается в том случае, когда поглощаемое вещество контактирует с неподвижным сорбентом. Статическая активность сорбента характеризуется количеством поглощаемого вещества на единицу массы сорбента в определенных условиях.

Динамическая сорбция наблюдается при фильтрации поглощаемого вещества через слой сорбента.

В случае гетерогенно-каталитических реакций считается, что число активных центров на единицу поверхности катализатора ограниченно. Кроме того, для упрощения считается, что каждый активный центр может удержать лишь определенное количество молекул или атомов реагирующего вещества (чаще всего одну). При таких предположениях скорость химического превращения оказывается пропорциональной концентрациям реагирующих веществ, адсорбированным на поверхности катализатора, т.е. поверхностным концентрациям. Для описания зависимости поверхностной концентрации некоторого вещества от его концентрации в объеме окружающего газа используется уравнение изотермы адсорбции Ленгмюра. Для упрощения принимают условия равновесия адсорбции и десорбции. Скорость адсорбции r_a (или u_адс) некоторого компонента можно принять пропорциональной его давлению Р и концентрации свободных активных центров, определяемой как разность между полной концентрацией активных центров С_а и концентрацией занятых центров С:

(53)

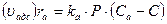
Скорость десорбции r_д (u_дес) пропорциональна концентрации занятых активных центров С:

(54)

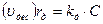
Предполагая равновесие между адсорбцией и десорбцией, т.е. приняв r_а = r_д (u_адс = u_дес) получим:

(55)

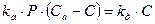
Следовательно, концентрация занятых активных центров равна:

введем замену 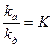-константа равновесия адсорбции (56)

В случае равенства k_а = k_десK=1, тогда получим:

(57)

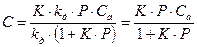
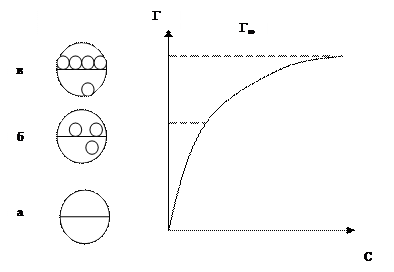
На рис.3 приведен пример изотермы адсорбции.

Адсорбция газов и паров на поверхности твердых тел также происходит в результате уменьшения свободной поверхностной энергии. На практике об адсорбции судят по количеству адсорбированного вещества, которое тем больше, чем больше поверхностный слой адсорбента, соответственно. Поэтому, для осуществления адсорбционных процессов необходимо использовать адсорбенты с высокоразвитой поверхностью. Важнейшими пористыми сорбентами являются активированный уголь и селикагель.

Рис. 3 Изотерма адсорбции.

Г – поверхностный избыток

а – чистый компонент

б – ненасыщенный мономолекулярный (в одну молекулу толщиной слой)

в – насыщенный мономолекулярный слой

Повышение температуры и понижение давления приводят к десорбции газов и паров. Вследствие этого сорбционные методы широкого использования в промышленности для извлечения различных веществ из воздушной среды и для разделения газов и паров.

Адсорбция растворенных веществ из растворов на твердых сорбентах всегда в большей или меньшей степени включает в себя адсорбцию растворителя. Изотермы адсорбции из растворов имеют вид, аналогичный изотермам адсорбции из газовой фазы.

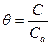
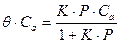
В практике моделирования гетерогенно-каталитческих процессов вместо поверхностных концентраций активных центров используют относительные концентрации , называемые обычно степенью заполнения активных центров. Уравнение (57) можно переписать, заменив в нем концентрации на степень заполнения активных центров:

(58)

Если процесс адсорбции сопровождается обратимой диссоциацией на n частиц, то скорости адсорбции и десорбции являются функциями n-степени от соответствующих концентраций:

Þ , тогда

или же

(59)

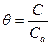
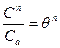
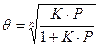
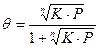
Если газовая фаза содержит несколько компонентов, адсорбируемых поверхностью катализатора, необходимо вычислить степень заполнения поверхности каждым компонентом.

º

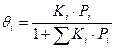
Необходимо учесть, что концентрация свободных мест определяется разностью между полной концентрацией активных центров и суммой центров, занятых всеми компонентами. Например, для двухкомпонентной системы:

(60)

(61)

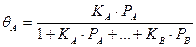
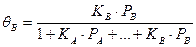
В случае диссоциации компонента А на две частицы получаем:

(62)

(63)

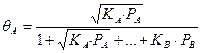
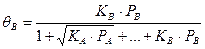
Если в газовой среде присутствует инертный компонент, не участвующий в химической реакции, но адсорбируемый поверхностью, в знаменатель выражений (59-63) соответствующее слагаемое, например:

(64)

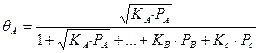
Так как скорость химического превращения пропорциональна поверхностным концентрациям реагирующих компонентов, т.е.

(65)

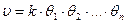
К примеру, для реакции типа А + В ® М при отсутствии диссоциации реагентов и без участия инертного компонента получается следующее выражение для скорости химического превращения:

(66)

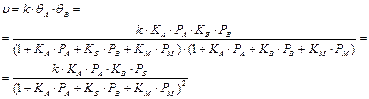
Степень в знаменателе выражения (66) равна количеству компонентов химической системы.

Если адсорбционные свойства компонентов реакции значительно разнятся, то вид уравнения Ленгмюра изменится. Пусть имеется реакция вида А ® Р, тогда

Рассмотрим различные варианты процесса:

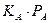
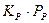
1. Если реагирующий газ А адсорбируется слабо, а продукт реакции – умеренно, то « « 1, то получим уравнение:

И тогда кинетическое уравнение примет вид:

Произведение 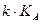называется кажущейся константой скорости реакции.

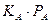
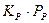
2. В случае сильной адсорбции реагирующего вещества и продукта реакции и значительно больше единицы, тогда уравнение для скорости реакции запишется как:

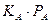
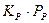
3. При слабой адсорбции реагирующего вещества и сильной адсорбции продукта реакции, « 1 и » 1, получим выражение:

4. При сильной адсорбции реагента и слабой адсорбции продукта получаем выражение:

( » 1 и » )

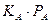
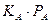
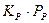
5. Если существует химическое взаимодействие адсорбированных молекул реагентов между собой (предположительно), то общий вид кинетического уравнения будет следующим:

(67)

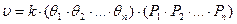
Для практических расчетов в ограниченной области режимных параметров часто используют аппроксимирующие степенные кинетические выражения:

(68)

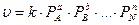
где a, b,…,n – частные порядки реакции.

К примеру, скорость окисления водорода до воды H₂ + O₂ → H₂O на палладиевом катализаторе при малой концентрации может быть описана уравнением:

(69)

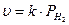
Надо добавить, что при моделировании в неизотермических условиях необходимо учитывать зависимость коэффициентов адсорбции и константы скорости от температуры. Что значительно усложняет модель.

Как видно, моделирование гетерогенных каталитических реакций – более сложный процесс по сравнению с моделированием гомогенных реакций, что связано с сильной нелинейностью получаемых уравнений.

Источник