Что такое диметрия в черчении

Диметрическая проекция

Диметрическая прое́кция — это аксонометрическая проекция, у которой коэффициенты искажения [1] по двум осям имеют равные значения, а искажение по третьей оси может принимать иное значение.

Содержание

Стандартные диметрические проекции [2]

Прямоугольная диметрическая проекция

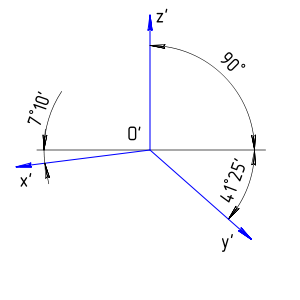
Ось Z’ расположена вертикально, а оси X’ и Y’ образуют с горизонтальной линией углы 7°10′ и 41°25′.

Коэффициент искажения по оси Y’ равен 0,47, а по осям X’ и Z’ 0,94. На практике используют приведённые коэффициенты искажения и . В этом случае изображение получается увеличенным в .

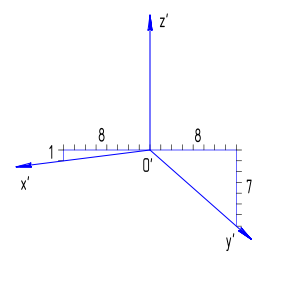
Приближённо аксонометрические оси стандартной диметрической проекции можно построить, если принять tg 7°10’=1/8, а tg 41°25’=7/8.

Фронтальная диметрическая проекция

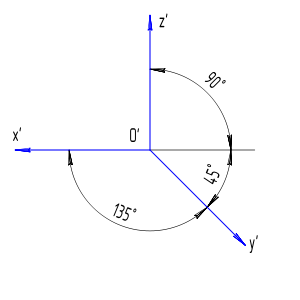
Коэффициент искажения по оси Y’ равен 0,5, а по осям X’ и Z’ 1. Допускается применять фронтальные диметрические проекции с углом наклона оси Y’ в 30° и 45°.

Применение

Диметрическая проекция используется в машиностроительном черчении, САПР для построения наглядного изображения детали на чертеже, а также в компьютерных играх для построения трёхмерного изображения.

Примечания

Литература

Полезное

Смотреть что такое «Диметрическая проекция» в других словарях:

ПРОЕКЦИЯ — (1) результат (см.) в виде (см.) на плоскости (поверхности) точки, линии, пространственного предмета и др. объектов; (2) один из способов получения в определённом масштабе изображения любого объёмного предмета (объекта) на плоскости.… … Большая политехническая энциклопедия

Проекция (геометрия) — У этого термина существуют и другие значения, см. Проекция. Проекции Параллельная Прямоугольная (ортогональная) Аксонометрическая Изометрическая Диметрическая Триметрическая Косоугольная Аксонометрическая Изометрическая Диметрическая… … Википедия

Аксонометрическая проекция — Проекции Параллельная Прямоугольная (ортогональная) Аксонометрическая Изометрическая Диметрическая Триметрическая Косоугольная Аксонометрическая Изометрическая Диметрическая Триметрическая Перспективная (центральная) … Википедия

Косоугольная проекция — Проекции Параллельная Прямоугольная (ортогональная) Аксонометрическая Изометрическая Диметрическая Триметрическая Косоугольная Аксонометрическая Изометрическая Диметрическая Триметрическая Перспективная (центральная) Прочие Птичий глаз Рыбий глаз … Википедия

Изометрическая проекция — Проекции Параллельная Прямоугольная (ортогональная) Аксонометрическая Изометрическая Диметрическая Триметрическая Косоугольная Аксонометрическая Изометрическая Диметрическая Триметрическая Перспективная (центральная) … Википедия

Ортогональная проекция — Проекции Параллельная Прямоугольная (ортогональная) Аксонометрическая Изометрическая Диметрическая Триметрическая Косоугольная Аксонометрическая Изометрическая Диметрическая Триметрическая Перспективная (центральная) Прочие Птичий глаз Рыбий глаз … Википедия

Параллельная проекция — Проекции Параллельная Прямоугольная (ортогональная) Аксонометрическая Изометрическая Диметрическая Триметрическая Косоугольная Аксонометрическая Изометрическая Диметрическая Триметрическая Перспективная (центральная) Прочие Птичий глаз Рыбий глаз … Википедия

Центральная проекция — Проекции Параллельная Прямоугольная (ортогональная) Аксонометрическая Изометрическая Диметрическая Триметрическая Косоугольная Аксонометрическая Изометрическая Диметрическая Триметрическая Перспективная (центральная) Прочие Птичий глаз Рыбий глаз … Википедия

Триметрическая проекция — Проекции Параллельная Прямоугольная (ортогональная) Аксонометрическая Изометрическая Диметрическая Триметрическая Косоугольная Аксонометрическая Изометрическая Диметрическая Триметрическая Перспективная (центральная) … Википедия

Параллельное проектирование — Проекции Параллельная Прямоугольная (ортогональная) Аксонометрическая Изометрическая Диметрическая Триметрическая Косоугольная Аксонометрическая Изометрическая Диметрическая Триметрическая Перспективная (центральная) Прочие Птичий глаз Рыбий глаз … Википедия

Источник

Что такое диметрия в черчении

Как построить диметрию детали?

Пять лет назад я написал урок на тему «Как построить изометрию?». Я знал, что пишу очень нужную статью, что такого подробного описания в сети просто нет. Но я и подумать не мог, что этот урок станет бестселлером. Каждый год к нему обращаются более 40 тысяч студентов, и я точно знаю, что не меньше трети из них обретают умение или, как минимум, перестают шарахаться от изометрии как от огня и начинают понимать, с какого бока к ней вообще надо подходить. И в том числе поэтому я крайне не рекомендую браться за урок построение диметрии если построение изометрии является для вас чем-то немыслимым. Дело в том, что в статье «построение изометрии детали» я очень подробно разобрал некоторые моменты, связанные с осями, их приложением к детали, и прочие нюансы, которые уже не будут так тщательно разобраны здесь.

При этом, как указано на рисунке, расстояния откладываемые вдоль осей X и Z откладываются без искажений (с приведенным коэффициентом 1), а расстояния вдоль оси Y откладываются с коэффициентом 0.5, т.е. уменьшаются в два раза. Благодаря такому расположению осей и линейным коэффициентам диметрия значительно эффективнее раскрывает наглядный вид деталей, в конструкции которых имеются четырех- и шестиугольные призмы. Кроме того, диметрия несколько экономичнее изометрии в плане занимаемого на листе пространства, но наверное актуальность этого уже в прошлом.

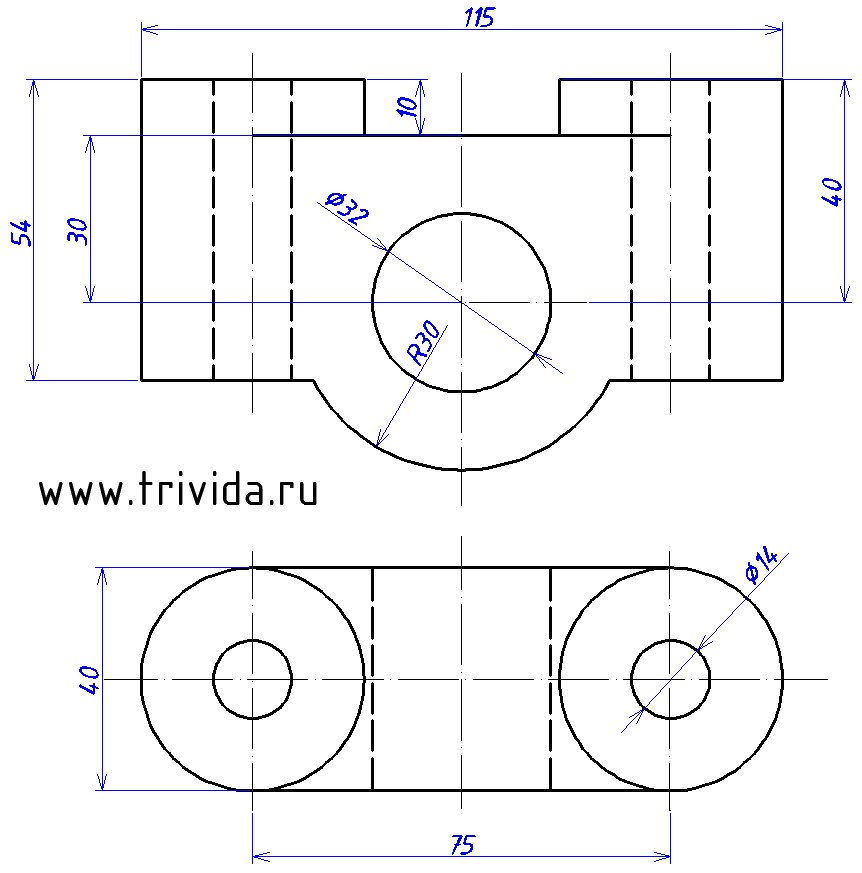
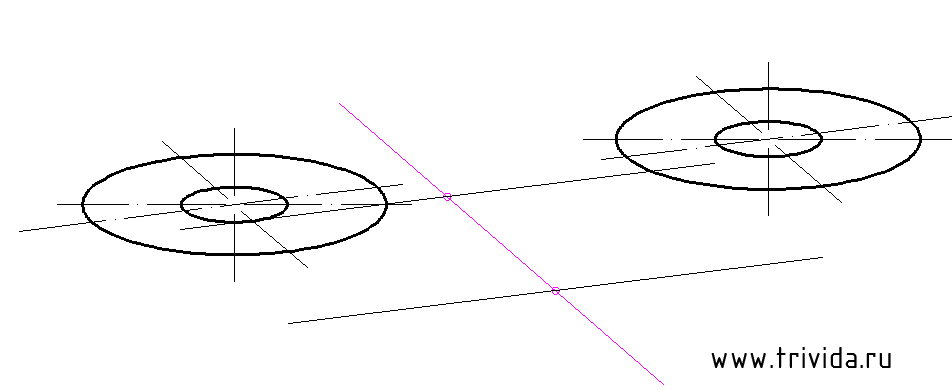
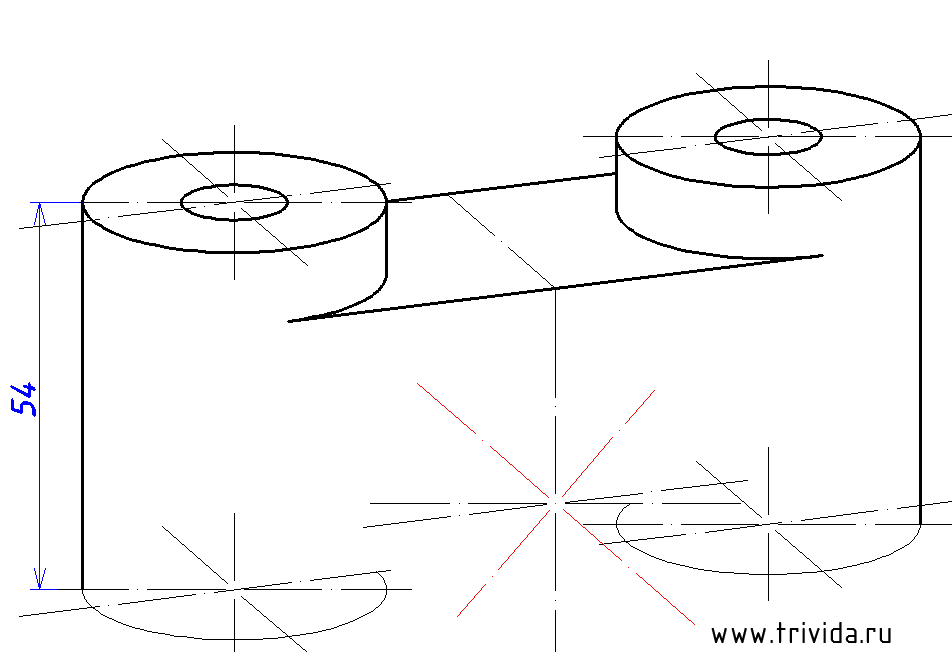
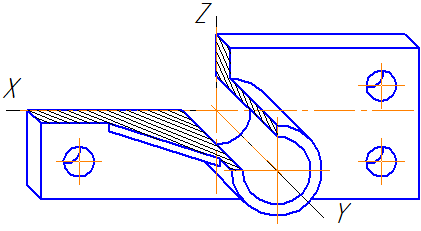
Итак, мы получили задание начертить диметрию вот такой детали. Ее можно описать как нечто похожее на бинокль, но вместо колесика для наведения резкости тут мы имеем сквозное отверстие диаметром 32мм. Сложно? В меру. Не совсем просто, но и не слишком накручено. То, что надо.

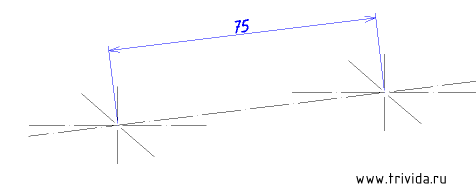
Воспользовавшись указанным способом построим два центра для наших будущих «окуляров». Они должны быть на расстоянии 75 мм отложенных вдоль оси X. (По сути нужно построить один центр по указанной технологии, затем отложить 75мм и через полученную точку провести оси, параллельные исходным)

Внимание: я не расписываю подробно, как построить красивый эллипс, зная две его оси. Этому у меня посвящен отдельный урок: как построить эллипс. Не совсем наш случай, но очень в тему еще один урок: «как начертить окружность в изометрии». Впрочем, если вы добрались до изучения диметрии, вы уже должны иметь представление о построении эллипсов.

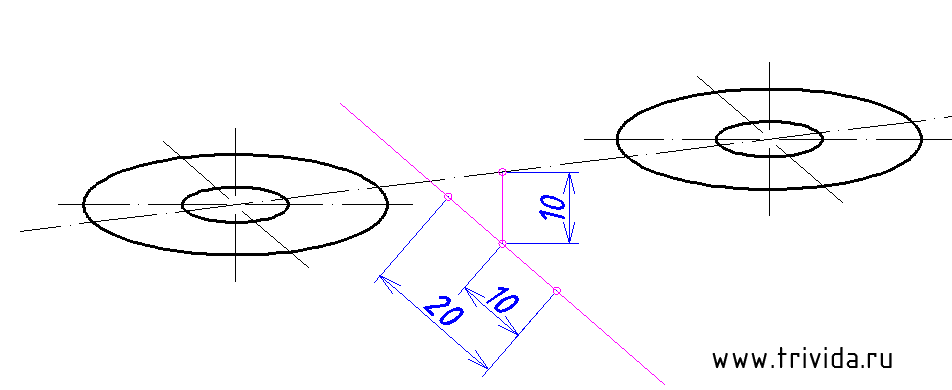
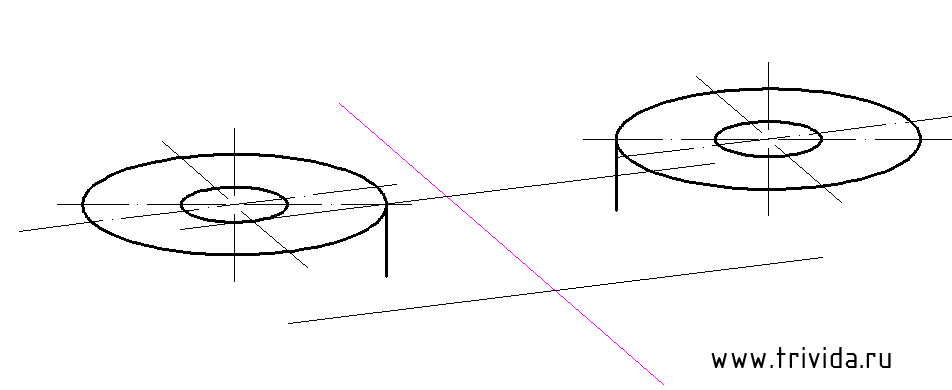
Согласно исходному чертежу наши «окуляры» на 10мм возвышаются над горизонтальной площадкой. Центр этой площадки расположен на 10 мм ниже середины отрезка, соединяющего центры наших эллипсов. А отложив по 10мм (почему не по 20? Потому что коэффициент 0.5, не забываем! )в каждую сторону вдоль оси Y, мы получим засечки, которые помогут нам прочертить границы этой горизонтальной площадки:

И, собственно, сами границы:

Теперь опустим вертикальные отрезки по 10мм от крайних точек больших эллипсов:

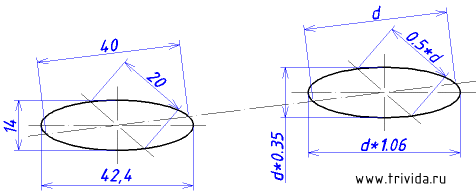
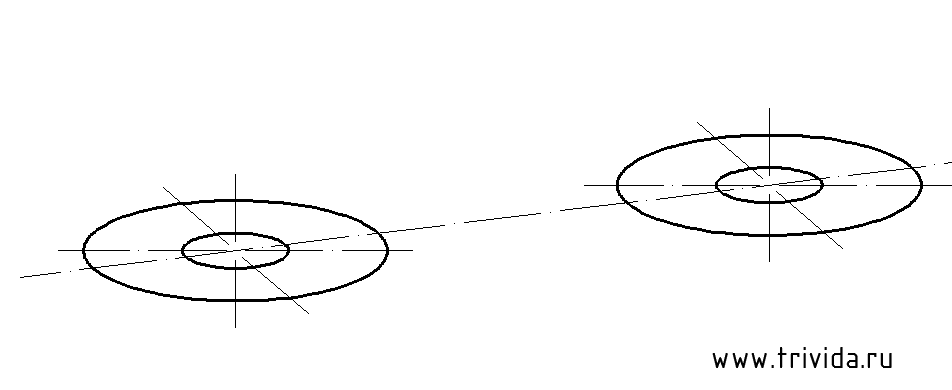
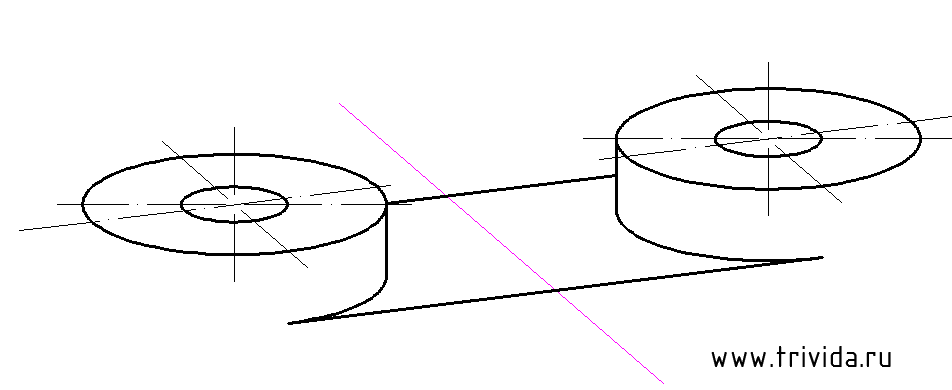
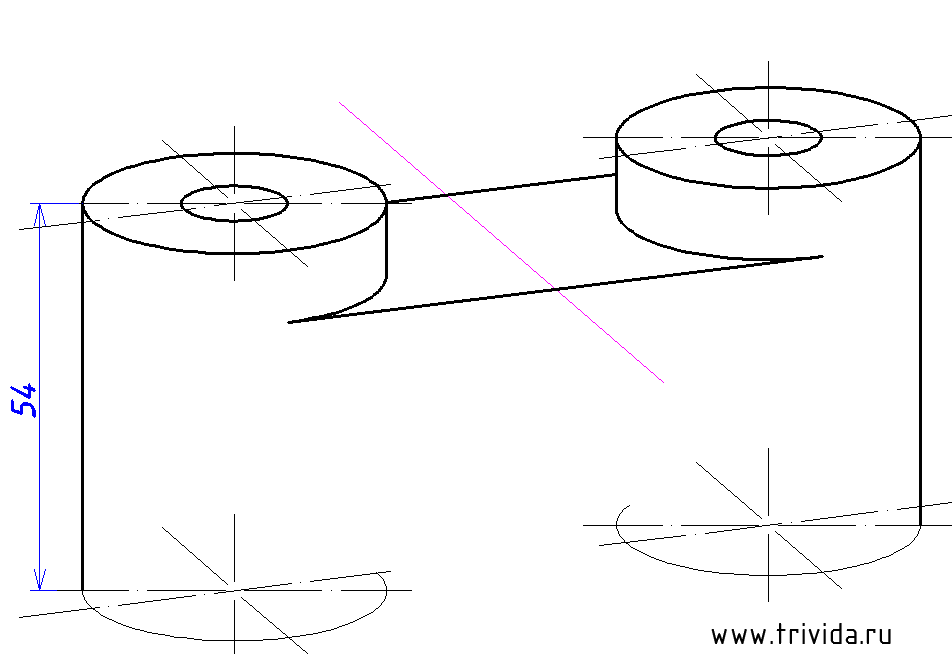
Строим центры нижних окружностей «окуляров». Они будут на 54мм ниже верхних центров. Кроме того, мы можем сразу провести крайние вертикальные боковые границы. Сами эллипсы строим или переносим, но пока в тонких линиях:

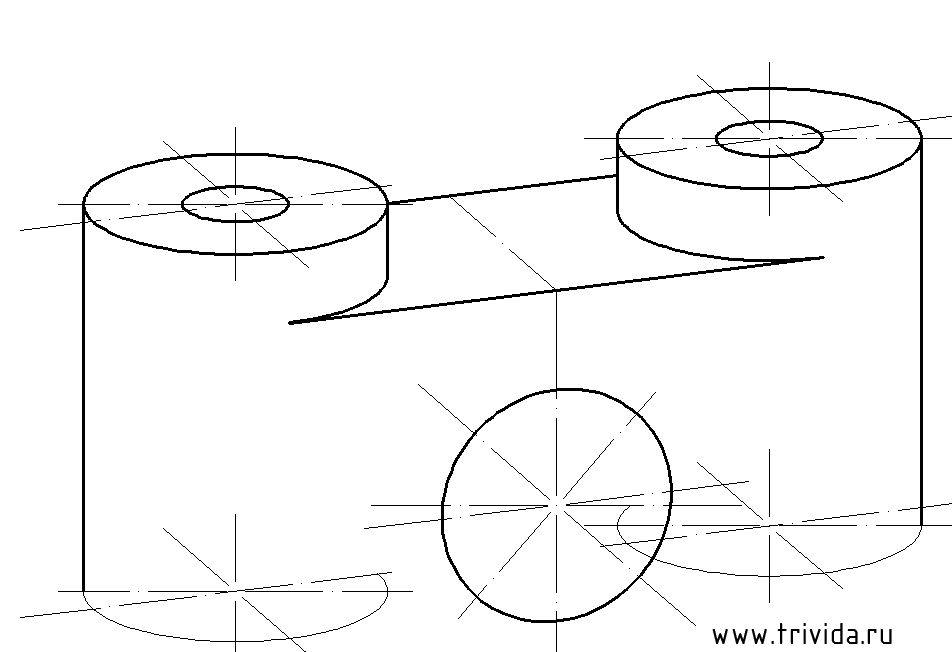
Пришло время заняться центральным отверстием. В отличии от уже построенных, центральная окружность лежит в другой плоскости, осью вращения в которой является ось Y. Ничего страшного нет, но нужно учесть два момента:
1. Большая ось эллипса будет перпендикулярна оси Y (такой оси мы сегодня еще не обозначали, это новое направление. Чтобы ни с чем не перепутать, оси данного эллипса я обозначил на рисунке красным цветом). Центр будет располагаться на 30 мм ниже горизонтальной площадки:

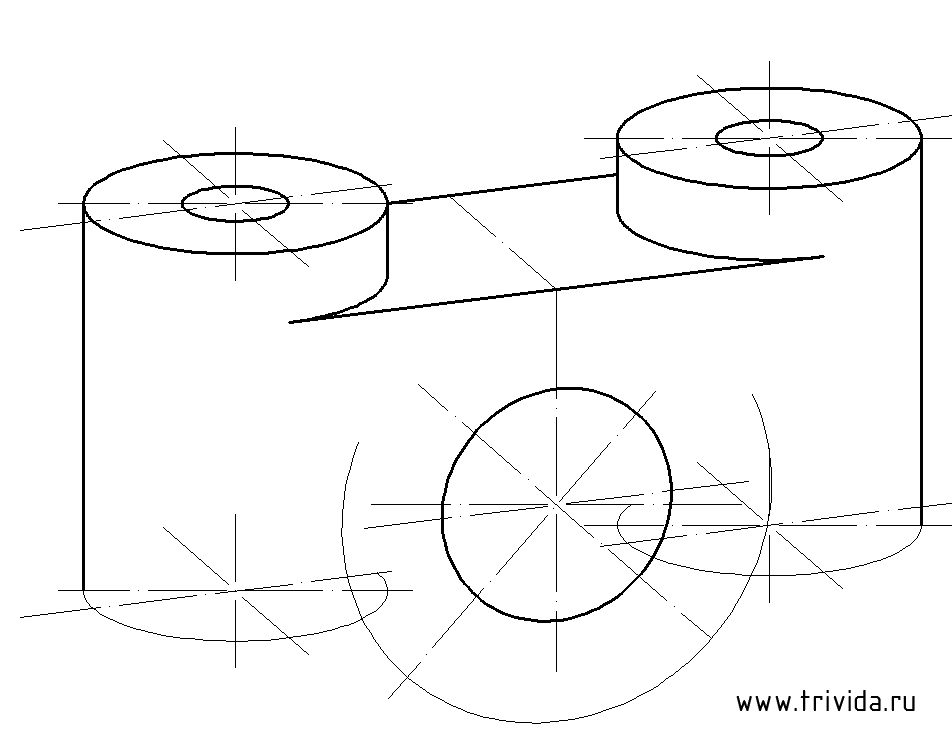
Остается построить еще один аналогичный эллипс с тем же центром. Исходные данные: диаметр 60мм, большая ось 63,6мм малая ось 57мм

Обозначив набросками наш последний эллипс, обводим его видимую часть, а так же ранее обозначенные нижние границы «окуляров» и стираем лишнее. Так же для приличия проведем отрезок, обозначающий границу цилиндрической поверхности (указан стрелкой). Возможно, про него никто бы и не вспомнил, но он есть, нужно прочертить:

Обратите внимание, у центрального отверстия появилась дальняя граница. Это копия эллипса, смещенная на 20мм вдоль оси Y. (Ширина детали 40мм, коэффициент по оси Y равен 0.5)

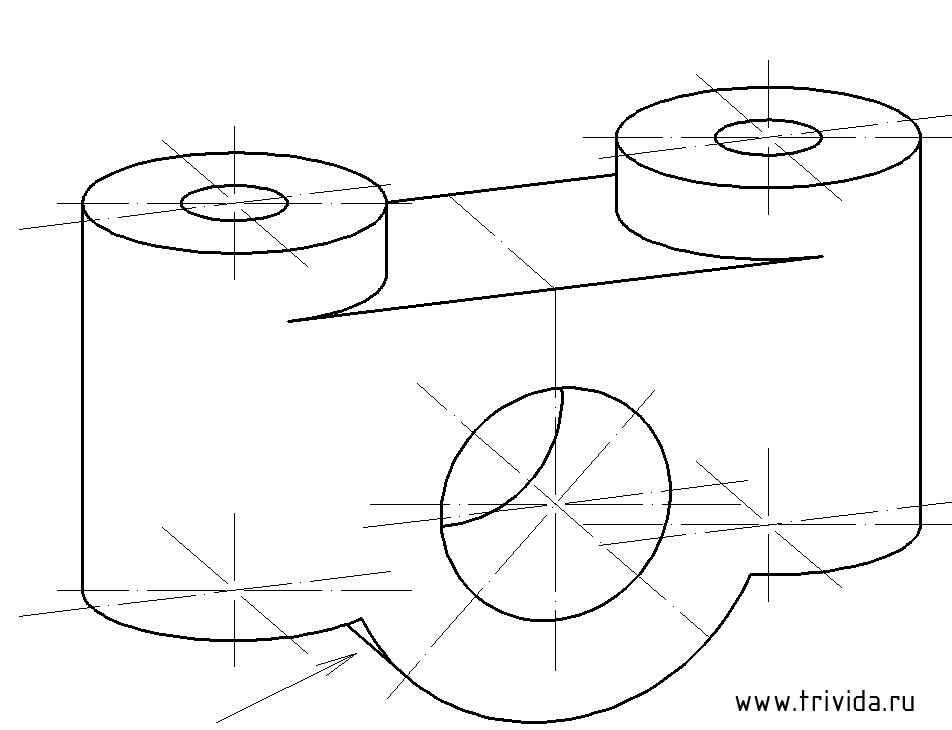
По сути, на этом наш урок «пошаговое построение диметрии» закончен. Однако, было бы неправильным, лишить вас самого интересного, и не отрезать четвертушку 🙂 Да, это потребуется не каждому, но зато для тех, кому придется данную процедуру выполнять, следующая картинка даст хороший наглядный материал, и наверняка поможет в неравной борьбе с домашним заданием:

Вот, теперь все. Ничего нового сюда уже не добавить. Если на вашей кафедре требуют, то в свободной зоне нужно вычертить и обозначить оси (направления, углы, названия), а в случае с вырезом четверти, не помешает и обозначение направления штриховки (в данном уроке не разбирается, но там ничего сложного, практически копия самой первой картинки в уроке).

До встречи на новых уроках!

Вы можете сказать «спасибо!» автору статьи:

пройдите по любой из рекламных ссылок в левой колонке, этим вы поддержите проект «White Bird. Чертежи Студентам»

Автор комментария: Vv
Дата: 2015-11-20

Большое спасибо, добрый человек!

Все-таки приятно, когда тебя называют добрым без сарказма!

Автор комментария: Роман
Дата: 2015-12-24

Очень полезно. Спасибо автору.

Автор комментария: Кир
Дата: 2016-04-01

Автор комментария: ивангай
Дата: 2016-11-21

Приветствую! Начните с урока про изометрию. Без этого у вас нет шансов. К сожалению это очень сложный материал, на него нельзя запрыгнуть на ходу.

Автор комментария: Юлия
Дата: 2017-05-02

Добрый день. Спасибо за урок (тут даже разрез сделан). Он очень полезен. Не нашла правда тут материала по построению триметрии. Будет ли?

Автор комментария: Юлия
Дата: 2017-05-02

Добрый день. Спасибо за урок (тут даже разрез сделан). Он очень полезен. Не нашла правда тут материала по построению триметрии. Будет ли?

Автор комментария: Александр
Дата: 2018-11-22

Статья полезная,но верхний чертёж начерчен неточно: не указана линия пересечения нижней центральной цилиндрической поверхности с нижней плоскостью.

Добавьте свой комментарий:

Наша страница в ВК:

чертежи Машиностроение и радио/приборостроение (специальность рк,РТ, ФАРМ и др.), строительные, 3D, печатные платы. Оформление по ескд. online. Компас, SolidWorks, P-Cad. Быстро, качественно. B96O1234@#$

Источник

Понятие об аксонометрических проекциях

Наглядные изображения применяют для пояснения чертежей деталей и машин. По ним легче представить форму предмета, чем по чертежу в трёх видах.

Одним из видов наглядных изображений являются аксонометрические изображения.

Аксонометрия в переводе с греческого означает «измерение по осям».

Аксонометрические проекции получают путём проецирования параллельными лучами

предмета, который связан с осями прямоугольных координат, на некоторую плоскость Р (рис. 103).

Таким образом, аксонометрическая проекция – это проекция только на одну плоскость.

Чтобы изображение получилось наглядным, проецирующие лучи не должны быть параллельны ни одной оси координат. Тогда на плоскости Р будут, хоть и с искажениями, изображены все три измерения предмета.

Аксонометрические проекции в зависимости от направления проецирования делятся на два вида: прямоугольные, когда направление проецирования перпендикулярно плоскости Р (угол φ=90°), и косоугольные, когда угол φ≠90°.

Если плоскость Р не параллельна ни одной из координатных плоскостей x,y,z, то на аксонометрической проекции у предмета искажаются все три его измерения. Если же плоскость Р параллельна одной или двум осям координат, то у предмета искажаются размеры соответственно по двум его измерениям или по одному.

Величина искажения определяется коэффициентом искажения, который равен отношению длины аксонометрической проекции отрезка, параллельного соответствующей оси координат, к его действительной длине. Любая аксонометрическая проекция имеет три коэффициента искажения по числу осей координат.

В зависимости от того, разные они или одинаковые, аксонометрические проекции делят на изометрические (коэффициенты искажения равны по всем трём осям) и триметрические (коэффициенты искажения по всем осям разные).

Стандартные виды аксонометрии. Изометрия. Диметрия

Наиболее распространёнными видами аксонометрических проекций являются прямоугольная изометрическая проекция (изометрия) и прямоугольная диметрическая проекция (диметрия), основные правила построения которых определены стандартом.

Прямоугольная изометрия представляет собой аксонометрическую проекцию с направлением проецирования, перпендикулярным к плоскости аксонометрических проекций одинаковыми по всем трём осям коэффициентами искажения, равными 0,82.

Оси изометрии (рис. 104а) составляют между собой углы 120°. Ось Z расположена вертикально. Для упрощения построения коэффициент искажения принимают равным 1.

Изображение при этом получается увеличенным, но вид его не меняется, т.к. сохраняется пропорциональность всех его размеров.

На рис. 104б и в приведены два способа построения осей в изометрии.

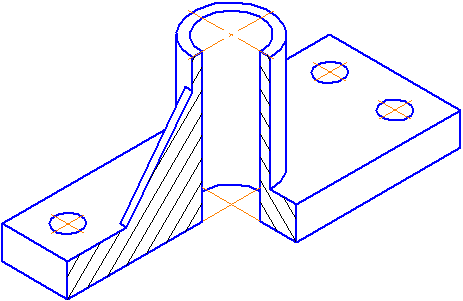
Прямоугольная диметрия представляет собой аксонометрическую проекцию с направлением проецирования, перпендикулярным аксонометрической плоскости проекций Р и одинаковыми коэффициентами искажения по осям х и z.

Ось х (рис. 105а) составляет с горизонтальной прямой угол 7°10′, а ось у – угол 41°25′.

Ось z занимает вертикальное положение. На рис. 105б показан графический способ построения осей диметрии.

В диметрии коэффициенты искажения по осям х и z равны 0,94, а по оси у – 0,47. При построениях первый коэффициент округляют до 1, а второй – до 0,5. Таким образом, отрезки, параллельные осям координат х и z, откладывают в натуральную величину, а длину отрезков, параллельных оси у, уменьшают в два раза.

Построение окружности в аксонометрии

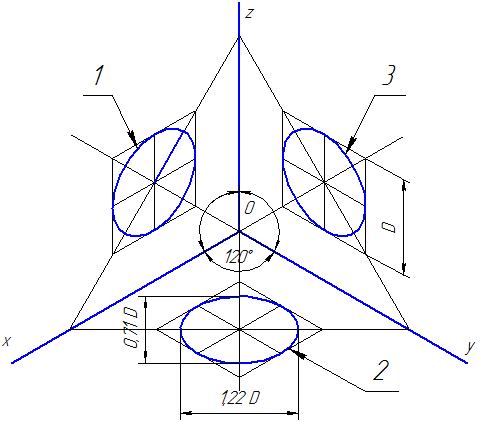
Изометрия. Изометрические проекции окружностей, расположенных в плоскостях проекций или в плоскостях, им параллельных, есть эллипсы (рис. 106).

Большие оси этих эллипсов равны l,22Dокр, а малые 0,71Dокр, где Dокр – диаметр изображаемой окружности. Большая ось эллипсов всегда перпендикулярна к той аксонометрической оси, которая отсутствует в плоскости окружности, а малая совпадает с этой осью или параллельна ей.

Практически при построении изометрии окружности эллипс обычно заменяют близким к нему по форме овалом, т.к. построение овала значительно проще.

Наиболее простой способ построения овала показан на рис. 107.

На рис. 108а,б построены изометрии окружностей, расположенных во фронтальной и профильной плоскостях.

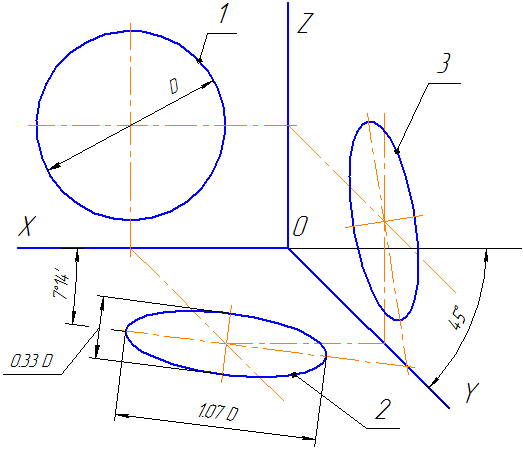
Окружности, расположенные во фронтальной плоскости, проецируются в виде эллипсов с большой осью, равной 1,06Dокр, а малой – 0,94Dокр. Большие оси эллипсов, как и в изометрии, перпендикулярны к той аксонометрической оси, которая отсутствует в данной плоскости, а малые оси совпадают с направлением этой оси.

Диметрии окружностей (эллипсы) обычно заменяют овалами, размеры осей которых равны размерам соответствующих осей эллипсов. Построение этих овалов показано на рис. 110. На рис. 110а построения понятны по чертежу.

На рис. 110б строим оси диметрии х_р, у_р, z_р. Затем строим прямую, перпендикулярную оси у_р. Отложив на осях х_р и z_р радиус заданной окружности, получим точки М, К, N, L, которые являются точками сопряжения дуг овала. Через точки М и N проводим горизонтальные прямые. В пересечении этих прямых с осью у_р и перпендикуляром к ней получим точки О₁, О₂, О₃, О₄. Из центров O₁ и О₃ опишем дуги радиусом R₁=О₃ K, а из центров О₂ и О₄ – дуги радиусом R₂=О₂M.

Аксонометрические изображения предметов

Приступая к построению аксонометрической проекции предмета, следует выбрать вид аксонометрии, обеспечивающий наибольшую наглядность изображения. Затем предмет связывают с системой прямоугольных координат, оси которой обычно совмещают с осями симметрии предмета. Только после этого можно приступить к построению аксонометрии.

Построение аксонометрии предмета обычно начинают с построения аксонометрии одной из его проекций (вторичной проекции). Затем полученное изображение дополняют построением третьего измерения всех его точек.

На рис. 111 показан пример построения прямоугольной изометрии предмета через построение его горизонтальной проекции.

На рис. 112 приведен пример построения прямоугольной изометрии детали путём построения её вторичной фронтальной проекции.

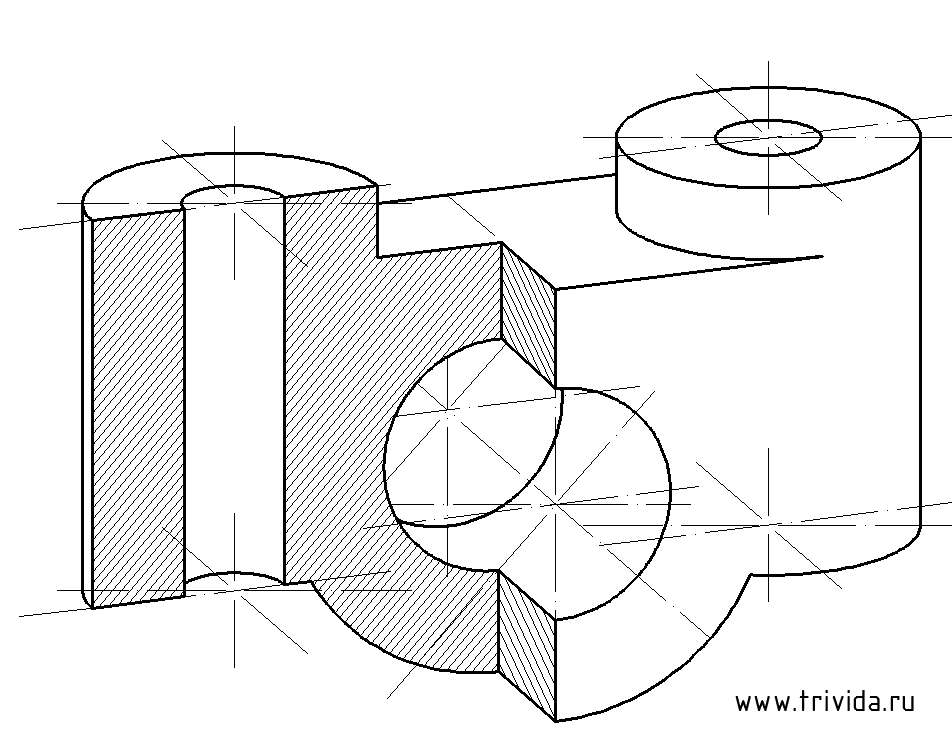
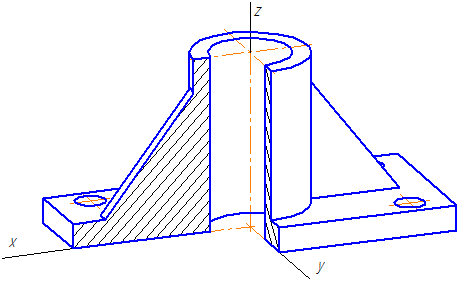
Для выявления внутренней формы предмета, изображённого в аксонометрии, в некоторых случаях применяют разрезы, которые условно называют вырезами. При этом используют две секущие плоскости, обычно совпадающие с плоскостями симметрии предмета (рис. 113).

рис. 111 рис. 112 рис. 113

Линии штриховки сечений в аксонометрических проекциях наносят параллельно одной из диагоналей проекций квадратов, лежащих в соответствующих координатных плоскостях. Стороны квадратов параллельны аксонометрическим осям (рис. 114).

Источник

Аксонометрические проекции

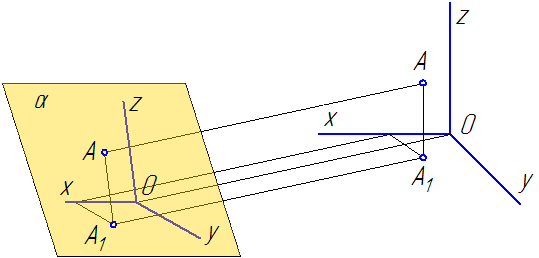
Способ аксонометрического проецирования состоит в том, что данный предмет вместе с осями прямоугольных координат, к которым эта система относится в пространстве, параллельно проецируется на некоторую плоскость α (Рисунок 4.1).

Рисунок 4.1
Направление проецирования S определяет положение аксонометрических осей на плоскости проекций α, а также коэффициенты искажения по ним. При этом необходимо обеспечить наглядность изображения и возможность производить определения положений и размеров предмета.
В качестве примера на Рисунке 4.2 показано построение аксонометрической проекции точки А по ее ортогональным проекциям.

Рисунок 4.2
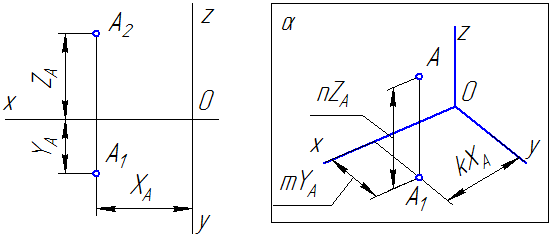
Здесь буквами k, m, n обозначены коэффициенты искажения по осям OX, OY и OZ соответственно. Если все три коэффициента равны между собой, то аксонометрическая проекция называется изометрической, если равны между собой только два коэффициента, то проекция называется диметрической, если же k≠m≠n, то проекция называется триметрической.
Если направление проецирования S перпендикулярно плоскости проекций α, то аксонометрическая проекция носит названия прямоугольной. В противном случае, аксонометрическая проекция называется косоугольной.
ГОСТ 2.317-2011 устанавливает следующие прямоугольные и косоугольные аксонометрические проекции:

Ниже приводятся параметры только трех наиболее часто применяемых на практике аксонометрических проекций.
Каждая такая проекция определяется положением осей, коэффициентами искажения по ним, размерами и направлениями осей эллипсов, расположенных в плоскостях, параллельных координатным плоскостям. Для упрощения геометрических построений коэффициенты искажения по осям, как правило, округляются.

4.1. Прямоугольные проекции

4.1.1. Изометрическая проекция

Направление аксонометрических осей приведено на Рисунке 4.3.

Рисунок 4.3 – Аксонометрические оси в прямоугольной изометрической проекции

Действительные коэффициенты искажения по осям OX, OY и OZ равны 0,82. Но с такими значениями коэффициентов искажения работать не удобно, поэтому, на практике, используются приведенные коэффициенты искажений. Эта проекция обычно выполняется без искажения, поэтому, приведенные коэффициенты искажений принимается k = m = n =1. Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются в эллипсы, большая ось которых равна 1,22, а малая – 0,71 диаметра образующей окружности D.

Большие оси эллипсов 1, 2 и 3 расположены под углом 90º к осям OY, OZ и OX, соответственно.

Пример выполнения изометрической проекции условной детали с вырезом приводится на Рисунке 4.4.

Рисунок 4.4 – Изображение детали в прямоугольной изометрической проекции

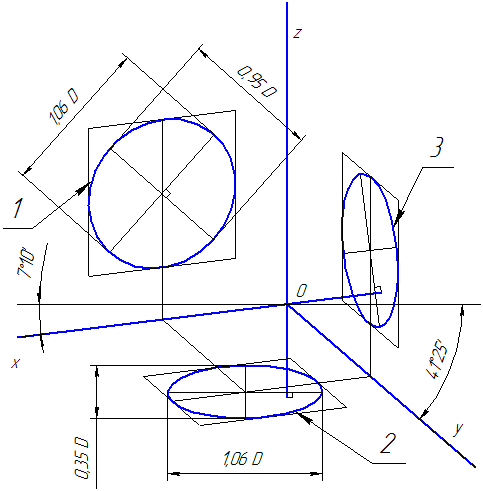
4.1.2. Диметрическая проекция

Положение аксонометрических осей проводится на Рисунке 4.5.

Для построения угла, приблизительно равного 7º10´, строится прямоугольный треугольник, катеты которого составляют одну и восемь единиц длины; для построения угла, приблизительно равного 41º25´ — катеты треугольника, соответственно, равны семи и восьми единицам длины.

Коэффициенты искажения по осям ОХ и OZ k=n=0,94 а по оси OY – m=0,47. При округлении этих параметров принимается k=n=1 и m=0,5. В этом случае размеры осей эллипсов будут: большая ось эллипса 1 равна 0,95D и эллипсов 2 и 3 – 0,35D (D – диаметр окружности). На Рисунке 4.5 большие оси эллипсов 1, 2 и 3 расположены под углом 90º к осям OY, OZ и OX, соответственно.

Пример прямоугольной диметрической проекции условной детали с вырезом приводится на Рисунке 4.6.

Рисунок 4.5 – Аксонометрические оси в прямоугольной диметрической проекции

Рисунок 4.6 – Изображение детали в прямоугольной диметрической проекции

4.2 Косоугольные проекции

4.2.1 Фронтальная диметрическая проекция

Коэффициент искажения по оси OY равен m=0,5 а по осям OX и OZ — k=n=1.

Рисунок 4.7 – Аксонометрические оси в косоугольной фронтальной диметрической проекции

Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются на плоскость XOZ без искажения. Большие оси эллипсов 2 и 3 равны 1,07D, а малая ось – 0,33D (D — диаметр окружности). Большая ось эллипса 2 составляет с осью ОХ угол 7º 14´, а большая ось эллипса 3 составляет такой же угол с осью OZ.

Пример аксонометрической проекции условной детали с вырезом приводится на Рисунке 4.8.

Как видно из рисунка, данная деталь располагается таким образом, чтобы её окружности проецировались на плоскость XОZ без искажения.

Рисунок 4.8 – Изображение детали в косоугольной фронтальной диметрической проекции

4.3 Построение эллипса

4.3.1 Построения эллипса по двум осям

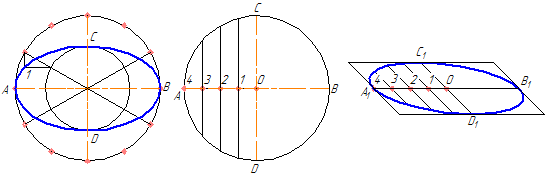
На данных осях эллипса АВ и СD строятся как на диаметрах две концентрические окружности (Рисунок 4.9, а).

Одна из этих окружностей делится на несколько равных (или неравных) частей.

Через точки деления и центр эллипса проводятся радиусы, которые делят также вторую окружность. Затем через точки деления большой окружности проводятся прямые, параллельные линии АВ.

Точки пересечения соответствующих прямых и будут точками, принадлежащими эллипсу. На Рисунке 4.9, а показана лишь одна искомая точка 1.

а б в
Рисунок 4.9 – Построение эллипса по двум осям (а), по хордам (б)

4.3.2 Построение эллипса по хордам

Диаметр окружности АВ делится на несколько равных частей, на рисунке 4.9,б их 4. Через точки 1-3 проводятся хорды параллельно диаметру CD. В любой аксонометрической проекции (например, в косоугольной диметрической) изображаются эти же диаметры с учетом коэффициента искажения. Так на Рисунке 4.9,б А₁В₁=АВ и С₁ D₁ = 0,5CD. Диаметр А ₁В₁ делится на то же число равных частей, что и диаметр АВ, через полученные точки 1-3 проводятся отрезки, равные соответственным хордам, умноженным на коэффициент искажение (в нашем случае – 0,5).

4.4 Штриховка сечений

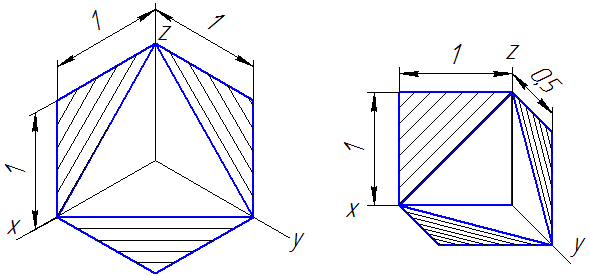
Линии штриховки сечений (разрезов) в аксонометрических проекциях наносятся параллельно одной из диагоналей квадратов, лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям (Рисунок 4.10: а – штриховка в прямоугольной изометрии; б – штриховка в косоугольной фронтальной диметрии).

а б
Рисунок 4.10 – Примеры штриховки в аксонометрических проекциях

Источник