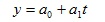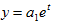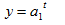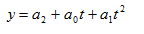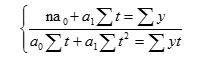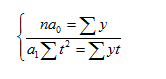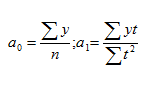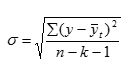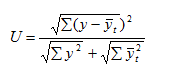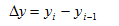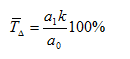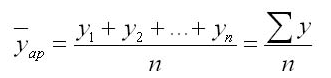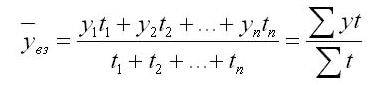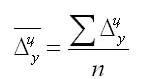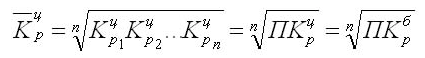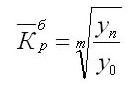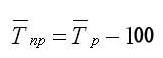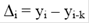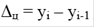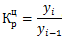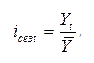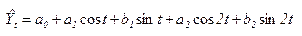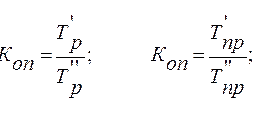Что такое динамический ряд
Ряды динамики
Понятие рядов динамики (временных рядов)
Одной из важнейших задач статистики является изучение изменений анализируемых показателей во времени, то есть их динамика. Эта задача решается при помощи анализа рядов динамики (временных рядов).
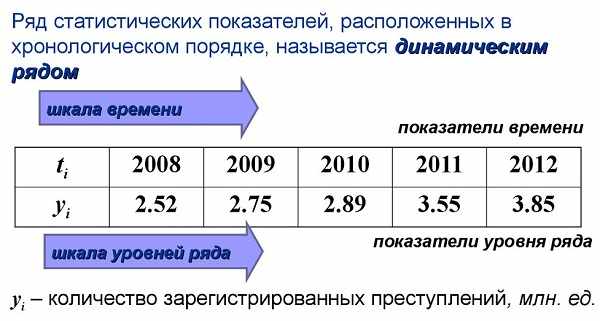
Ряд динамики (или временной ряд) – это числовые значения определенного статистического показателя в последовательные моменты или периоды времени (т.е. расположенные в хронологическом порядке).
Числовые значения того или иного статистического показателя, составляющего ряд динамики, называют уровнями ряда и обычно обозначают буквой y. Первый член ряда y1 называют начальным или базисным уровнем, а последний yn – конечным. Моменты или периоды времени, к которым относятся уровни, обозначают через t.
Ряды динамики, как правило, представляют в виде таблицы или графика, причем по оси абсцисс строится шкала времени t, а по оси ординат – шкала уровней ряда y.
Пример ряда динамики
Таблица. Число жителей России в 2004-2009 гг. в млн.чел, на 1 января
| Год | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 |
| Число жителей | 144,2 | 143,5 | 142,8 | 142,2 | 142,0 | 141,9 |
График ряда динамики числа жителей России в 2004-2009 гг. в млн.чел, на 1 января
Данные таблицы и графика наглядно иллюстрируют ежегодное снижение числа жителей России в 2004-2009 годах.
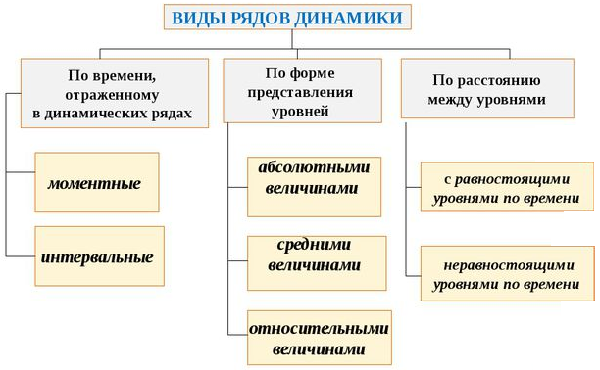
Виды рядов динамики
Ряды динамики классифицируются по следующим основным признакам:
В нашем примере про число жителей России ряд динамики: 1) моментный (приведены уровни на 1 января); 2) абсолютных величин (в млн.чел.); 3) равномерный (равные интервалы в 1 год); 4) изолированный.
Показатели изменения уровней ряда динамики
Анализ рядов динамики начинается с определения того, как именно изменяются уровни ряда (увеличиваются, уменьшаются или остаются неизменными) в абсолютном и относительном выражении. Чтобы проследить за направлением и размером изменений уровней во времени, для рядов динамики рассчитывают показатели изменения уровней ряда динамики:
Все эти показатели могут определяться базисным способом, когда уровень данного периода сравнивается с первым (базисным) периодом, либо цепным способом – когда сравниваются два уровня соседних периодов.
Базисное абсолютное изменение представляет собой разность конкретного и первого уровней ряда, определяется по формуле
Оно показывает, на сколько (в единицах показателей ряда) уровень одного (i-того) периода больше или меньше первого (базисного) уровня, и, следовательно, может иметь знак «+» (при увеличении уровней) или «–» (при уменьшении уровней).
Цепное абсолютное изменение представляет собой разность конкретного и предыдущего уровней ряда, определяется по формуле
Оно показывает, на сколько (в единицах показателей ряда) уровень одного (i-того) периода больше или меньше предыдущего уровня, и может иметь знак «+» или «–».
В следующей расчетной таблице в столбце 3 рассчитаны базисные абсолютные изменения, а в столбце 4 – цепные абсолютные изменения.
| Год | y |  |  |  |  |  , % , % |  ,% ,% |
| 2004 | 144,2 | ||||||
| 2005 | 143,5 | -0,7 | -0,7 | 0,995 | 0,995 | -0,49 | -0,49 |
| 2006 | 142,8 | -1,4 | -0,7 | 0,990 | 0,995 | -0,97 | -0,49 |
| 2007 | 142,2 | -2,0 | -0,6 | 0,986 | 0,996 | -1,39 | -0,42 |
| 2008 | 142,0 | -2,2 | -0,2 | 0,985 | 0,999 | -1,53 | -0,14 |
| 2009 | 141,9 | -2,3 | -0,1 | 0,984 | 0,999 | -1,60 | -0,07 |
| Итого | -2,3 | 0,984 | -1,60 |
Между базисными и цепными абсолютными изменениями существует взаимосвязь: сумма цепных абсолютных изменений равна последнему базисному изменению, то есть

Базисное относительное изменение (базисный темп роста или базисный индекс динамики) представляет собой соотношение конкретного и первого уровней ряда, определяясь по формуле
Цепное относительное изменение (цепной темп роста или цепной индекс динамики) представляет собой соотношение конкретного и предыдущего уровней ряда, определяясь по формуле

Относительное изменение показывает во сколько раз уровень данного периода больше уровня какого-либо предшествующего периода (при i>1) или какую его часть составляет (при i Следующая лекция.
Динамические ряды — краткое руководство по анализу изменений явлений во времени
Даная статья понятными и простыми терминами объяснит, что же такое динамические ряды, для чего они нужны, как производится анализ полученных данных и какие возможности открываются перед теми, кто владеет методикой данного анализа. Любое явление в области здравоохранения нуждается в тщательной оценке, и здесь знания анализа динамических рядов неоценимы. С помощью динамического ряда можно оценить и спрогнозировать проблематику любой нозологической единицы, сформировать дальнейшую тактику лечения и меры профилактики заболеваний.
Динамический ряд — ряд однородных величин, характеризующих изменение явления во времени.
Целью анализа динамических рядов является:
Числовые значения, составляющие динамический ряд, называются уровнями ряда (у).
Типы динамических рядов:
а) простые (уровень ряда выражен абсолютными числами);
б) сложные (уровень ряда выражен обобщающими коэффициентами).
а) моментные (данные собираются на определенный момент времени);
б) интервальные (данные собираются за определенный период времени).
а) с выраженной тенденцией (r =0,7 — 1,0);
б) с неустойчивой тенденцией (r =0,3 — 0,69);
в) с отсутствием тенденции ( r = 0 — 0,29).
Основное требование, предъявляемое к анализируемым динамическим рядам, заключается в сопоставимости их уровней. Для оценки сопоставимости проводят предварительный анализ полученных данных по следующим критериям:
Методика анализа динамических рядов
Методика аналитики предусматривает выполнение последовательных действий:
Способы выравнивания динамических рядов
Чтобы произвести выравнивание динамических рядов потребуются следующие действия:
При этом способе на основании фактических данных подбирается наиболее подходящее для отражения тенденции развития явления математическое уравнение (аппроксимирующая функция), которое принимается за модель развития явления во времени. Т.е. уровни ряда рассматриваются как функция времени, и задача выравнивания сводится к определению вида функции, отысканию ее параметров по эмпирическим данным и расчету по найденной формуле теоретических выравненных уровней. Наиболее часто используются следующие функции:
а) линейная зависимость:
б) экспоненциальная зависимость:
в) показательная зависимость:
г) параболическая зависимость:
у – теоретический уровень;
t – временной интервал.
где у — уровни фактического ряда;
n — количество уровней;
t — порядковый номер временного периода.
При отсчете времени от середины ряда St = 0 и система нормальных уравнений принимает вид:
Отсюда находим параметры уравнения:
Подставляя в уравнение у = а0 + а1t вместо «t» его ранги, находим выравненные (теоретические) значения уровней ряда и строим теоретическую кривую выравненного динамического ряда.
При использовании аналитического способа всегда отмечается отклонение теоретических уровней от фактических уровней ряда, которое может быть обусловлено как случайными колебаниями, так и неправильно подобранным аппроксимирующим уравнением. В связи с этим заключительным этапом выравнивания динамического ряда аналитическим способом является оценка точности аппроксимации с определенным уровнем значимости.
Оценка точности аппроксимации возможна с помощью нахождения
Для получения точной оценки необходимо найти такие величины:
а) коэффициент вариации:

где у- фактический уровень ряда;
yt — теоретический уровень ряда;
k- число параметров уравнения;
n- число уровней ряда.
Аппроксимация считается точной при Cv не более 15%.
б) коэффициент расхождения Тейла:
где у — фактический уровень ряда;
yt — теоретический уровень ряда.
Аппроксимация считается точной при U не более 5%
После аналитического выравнивания динамического ряда и описания тренда возможно экстраполировать полученные данные. Экстраполяция — предположение о сохранении тренда, базирующееся на допущении неизменности влияющих факторов и предшествующей тенденции. Осуществляется путем подставления в найденное уравнение аппроксимации не фактического значения временного интервала, а предполагаемого порядкового номера (ранг) того периода, на который прогнозируется результат.
Вычисление основных показателей динамического ряда
Алгоритм вычислений ведущих параметров динамических рядов:
yi- текущий уровень (сравниваемый);
уi-1— базисный уровень (с каким сравнивают);
t- период времени, в течение которого уровень предполагается неизменным.
1.Абсолютный прирост (убыль) :
3.Темп прироста (относительная скорость), темп убыли :
4.Средний темп прироста (убыли):
где а0; а1 — параметры уравнения;
k = 1 при нечетном ряде;
k = 2 при четном ряде.
5.1% прироста (убыли): используются при сравнении динамических рядов с уровнями, выраженными различными обобщающими коэффициентами.
Таким образом, с помощью данного руководства по определению и расчетам такого понятия, как, динамические ряды, специалисты различных отраслей медицины, ученые могут эффективно и быстро оценить изменение различных величин в течение времени.
Благодарим за интерес, проявленный к нашей статье, оставайтесь с нами!
Ряды динамики в статистике
Ряд динамики может состоять из:
Виды рядов динамики
Объединение радов происходит по:
Чтобы без ошибок построить динамические ряды, необходимо сопоставлять уровни рядов разных периодов. Для этого у них должны быть однородные величины. Также ряды предполагают охват явления с одинаковой полнотой.
Не допускать погрешностей в анализе динамики помогает смыкание рядов динамики. Суть понятия в проведении подготовительной работы до основных расчетов. Во время подготовки ряды объединяются в один. Уровни этих рядов рассчитаны по разным методологиям. Смыкание также включает преобразования, при которых абсолютные уровни рядов приводятся к общему основанию. Это действие помогает избежать несопоставимости уровней.
Анализ показателей в рядах динамики
Ряд динамики характеризует изменения данных внутри этого ряда. Статистические данные необходимо сравнивать также между рядами. По формулам можно определить основные показатели.
Разность уровней ряда динамики называется абсолютным приростом. Показатель демонстрирует, на сколько изменился каждый последующий уровень.
Отношение уровней ряда динамики называется темпом (коэффициентом) роста. По нему видно, во сколько раз изменились последовательные значения.
Темп прироста. Показывает процентное отличие между последовательными уровнями.
Если сравнивать между собой числа без всякой системы, не получится грамотно проанализировать ситуацию и выстроить новую стратегию. Например, продвижение продукта на основе маркетинговой стратегии. Использование формул поможет высчитать, какую прибыль принесло компании конкретное решение за анализируемый период.
Анализ показателей за длительный промежуток
Если есть задача оценить изменения, которые касаются длинного временного отрезка, эффективно применить средние показатели. В статистике для их определения используются следующие понятия.
Средний уровень ряда динамики. Применим для интервальных равноотстоящих рядов
Если ряды неравноотстоящие, средний уровень интервального ряда динамики определяется как
Использование перечисленных методов позволяет применять полученные значения в экономике. Определять эффективность финансовых вложений, прогнозировать результаты. В управление предприятиями и бухгалтерию также можно внедрить данные методы для планирования и распределения бюджета.
Динамический ряд, уровни, виды. Показатели динамического ряда. Выравнивание динамического ряда



Динамический ряд – это ряд статистических однородных величин, показывающих изменение какого-то явления в последовательные периоды времени. Его называют также хронологическим.
Числа, составляющие динамический ряд, являются уровнями динамического ряда.
Ряды могут быть простыми и сложными. В простых рядах уровни ряда представлены абсолютными величинами. Различают два вида простых рядов: интервальный и моментный.
Интервальный ряд состоит из последовательного ряда уровней, характеризующих изменение явления за определенный интервал времени.
Моментный ряд представлен уровнями, определяющими размеры явления на определенную дату (момент).
Сложный динамический ряд формируется из относительных или средних величин (уровней).
Динамический ряд характеризуют следующие показатели:
– абсолютный прирост (убыль) ряда (показывает разность между последующим и предыдущим уровнем динамического ряда);
– темп прироста или снижения (выражает отношение абсолютного прироста к предыдущему уровню динамического ряда в % и показывает, на сколько процентов увеличился (снизился) последующий уровень, по сравнению с предыдущим);
– абсолютное значение 1 % прироста или убыли (выражает отношение абсолютного прироста к темпу прироста);
– темп роста(представляет процентное отношение последующего уровня к предыдущему уровню);
– показатель наглядности (показывает отношение каждого уровня ряда к одному из них, чаще начальному, принятому за 100%).
С целью выявления основных закономерностей, свойственных явлению за наблюдаемый период, применяют следующие методы выравнивания динамического ряда:
– укрупнение ряда (суммирование данных соседних периодов);
– расчет групповой средней – определение средней величины каждого укрупненного периода (интервала);
– расчет скользящей средней (каждый уровень ряда заменяется на среднюю из данного уровня и двух соседних с ним);
Рассмотрим пример выравнивания динамического ряда по методу укрупнения интервалов (столбец 3) и сглаживания ряда методом групповой скользящей средней (столбцы 4, 5 и 6): 3
1. Проводим группировку по трем периодам наблюдения (∑Хi).
2. Рассчитываем среднюю по укрупненным интервалам (Х).
3. Проводим группировку с отступом на один показатель (1,2,3;2,3,4;3,4,5 и т.д.). 3
Вычисляем Yi+1по следующей формуле: Yi+1 = (∑Хi).
Например: Y2 = 3,5+2,8+3,6;Y3 = 2,8+3,6+3,7 и т.д.
4. Рассчитываем скользящую среднюю (`y), как (`y =∑Yi+1/3)
Таблица 1.1 Исходные данные и результаты выравнивания динамического ряда
Ряды динамики в статистике
Статистика занимается не только обработкой накопленных данных, но и нахождением тенденций в различных парных показателях, которые связаны друг с другом, что успешно решается применением инструмента «ряды динамики в статистике».
Классическим примером является изменение каких-либо показателей за определенный промежуток времени, что в конце концов сводится не к изучению попарной зависимости (показатель время), а к изучению изменений показателей в динамике.
Понятие о рядах динамики
Строгое понятие для ряда динамики обозначено в статистике так.
Динамические ряды (иными словами ряд динамики или временной ряд) – это распределенные в увеличивающемся порядке дискретных значений выбранного статистического параметра за последовательные временные промежутки.
Если рассмотреть динамический ряд, будет очевидно, что он наполнен данными в формате y1t1, y2t2, y3t3…yntn. Применительно к временному ряду, значением у будет называться «уровень ряда», при этом первый член ряда (у1) называется базисным (начальным) уровнем, а уn – конечным уровнем. Через обозначение t будет обозначаться временной показатель, который соответствует каждому из уровней ряда.
При построении графической зависимости временного ряда, функция будет иметь вид t(y), где по оси y (ординат) будут отложены значения уровней ряда (параметр у), а по оси х (ось абсцисс) будут отложены временные значения параметра t.
Пример ряда динамики и его характеристика
В качестве примера, рассмотрим следующий ряд.
Таблицу можно озаглавить так: «Годовой выпуск препарата «Ибупрофен» в 2013-2018гг. в млн. уп.»
| Год | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
| Годовой объем выпуска, млн. уп. | 88,1 | 91,3 | 96,5 | 99,3 | 101,8 | 100,7 |
В данном ряду можно обнаружить присутствие следующих показателей:
На основании изложенного, можно сделать вывод, что перед нами находится временной ряд.
Виды рядов динамики
В зависимости от характеризующего критерия, существует несколько разновидностей динамических рядов.
По временной характеристике различают моментальные и интервальные:
При характеристике по показателю t выделяют неполные и полные ряды. Неполными считаются такие, в которых не соблюдается одинаковый промежуток между соседними значениями времени. Для полных, такой интервал соблюден.
Кроме этого, существует классификация по количеству показателей. Существуют изолированные – во времени анализируется всего один показатель и многомерные, когда во времени анализ ведется для целого ряда параметров, которые связаны между собой одним процессом.
Правила построения рядов динамики
Когда производится построение временных рядов, то для них должны соблюдаться общие требования:
Средние характеристики ряда динамики
Главный показатель, характеризующий среднее значение абсолютных показателей (y1, y2…yn) – это средний уровень ряда. Если основные интервалы не изменялись, то следует пользоваться выражением для расчета (где t – количество уровней):
Чуть сложнее будет выглядеть методика расчета, если были временные пропуски или они неравны. Вычисления выполняются через арифметическую взвешенную:
Здесь y1, y2…yn – это абсолютные уровни ряда, а t1, t2…tn – протяженности временных интервалов.
Для описания удобно пользоваться параметром среднего абсолютного прироста, представляющим собой среднее от прироста за равные временные промежутки. Когда использованы гармоничные интервалы, формула выглядит так:
Для приведенного выражения обозначение n – это число приростов за выбранный период.
Также есть методика расчетов с использованием базисного абсолютного прироста при равенстве интервалов для смыкания рядов:
Значение m – это количество уровней в выбранном периоде.
Показательная характеристика средний темп роста, он отображает как происходило изменение уровней рядя (коррелируя с единицами времени). Вычисления для цепных показателей выведены через расчет средней геометрической:
В данном выражении n количество цепных коэффициентов, Кц – сами цепные коэффициенты.
Когда даны все значения уровней, то выражение значительно упрощается:
Иногда требуется охарактеризовать срединный темп прироста, рассчитывающийся по уравнению на основании уже известных средних темпов роста (Тр):
Показатели анализа рядов динамики
Всего имеются 5 характеристик, предназначающихся для выполнения анализа:
Анализ сезонных колебаний
Если взять для анализа временной ряд, в котором собраны объемы продаж противовирусных препаратов за 5 лет, то будет очевидно, что ежегодно происходят колебания (снижение или увеличение) продаж, которые повторяются. Такие колебания будут именоваться сезонными.
Чтобы устранить нежелательное влияние таких колебаний, проводится аналитическое изучение, выполняющееся либо с помощью гармонического исследования, либо с учетом индекса сезонности.
Индекс сезонности это фактическая характеристика того, в какое количество раз анализируемый уровень увеличен или уменьшен относительно срединного:
Тут Yt – это уровень, предполагаемый к анализу, а Ȳ это средний уровень всего ряда.
Более сложный анализ предполагает выделение гармонических колебаний. Для этого производится выравнивание по ряду Фурье (так называемые «гармоники»), и высчитывают, какие гармоники наиболее сопоставимы с анализируемым рядом. Общий вид ряда Фурье для двух гармоник выражается формулой:
Индекс сезонности
Для того чтобы не вычислять относительную разницу в процентах между каждым месяцем во временном ряду, можно вычислить один параметр – индекс сезонности.
Индекс сезонности рассчитывается на основании следующих показателей:
По результатам сопоставления получается значение, которое так или иначе соотносится с уровнем в 100%. Если присутствует значимое отклонение в меньшую сторону, то это является свидетельством присутствия сезонного колебания.
Приведение рядов динамики к одинаковому основанию
Во время работы с несколькими явлениями, описывающими один процесс, может вызывать интерес сопоставление рядов динамики. С целью корректного сопоставления потребуется приведение к одному основанию. Сопутствующей операцией является вычисление коэффициента опережения или отставания.
К каждому ряду находится базисный уровень и вычисляются темпы роста и прироста рядов. Для каждого ряда должен быть выбран аналогичный временной интервал.
Сравнение проводится на основании отношения базисного темпа роста (опционально – прироста) в аналогичном временной интервале. Выражения для расчета достаточно просты:
Аналитическое выравнивание ряда динамики
При определении каких-либо закономерностей во временных рядах и возможности прогнозирования отдельных тенденций, применяется методика аналитического выравнивания. С этой целью производится приближение к определенной алгебраической зависимости, наиболее точно описывающей ряд.
Методика укрупнения интервалов представляет собой преобразование, когда временные промежутки делаются более длительными, что позволяет более точно оценить общий вектор тенденции и понять, какое направление будет иметь зависимость.
Методика скользящей средней основана на особенности временных рядов погашать случайные отклонения от среднего уровня. Каждому звену с использованием простого среднеарифметичнского значения нужно рассчитывать уровень, в котором рандомные колебания сведены к минимуму.
Методика аналитического выравнивания под конкретный ряд подбирается зависимость, которая более полно отражает алгебраическую зависимость.
Примеры решения задач на тему «Ряды динамики в статистике»
Классическим упражнением является определение вида и показателей для ряда динамики.
Задача. Для указанного временного ряда высчитать: его вид, цепной и базисный прирост, темп роста/прироста, средний темп прироста.
| Отчетный год | Суммарный объем производства, млрд. руб. |
| 2014 | 18 |
| 2015 | 16 |
| 2016 | 17 |
| 2017 | 16 |
| 2018 | 12 |
Согласно определению, этот ряд динамики относится к интервальному, поскольку в условии приведен четкий промежуток времени. Произведем расчет показателей.
Абсолютные приросты (по цепному способу):
16 – 18 = 2 млрд. руб.
17 – 16 = 1 млрд. руб.
16 – 17 = 1 млрд. руб.
12 – 16 = 4 млрд. руб.
Абсолютные приросты (по базисному методу):
17 – 18 = 1 млрд. руб.
12 – 18 = 6 млрд. руб.
Цепные темпы роста:
Базисные темпы роста:
Цепные темпы прироста:
Базисные темпы прироста:
Средний уровень временного ряда:
(18 + 16 + 17 + 16 + 12) / 5 = 15,8.
Среднегодовой абсолютный прирост:
Среднегодовой темп прироста:
Таким образом временные ряды занимают важное место среди статистических объектов.
Основное их преимущество заключается в широком практическом применении, которое позволяет использовать ряды динамики для наблюдений за физическими величинами и экономическими показателями. Важно знать о нюансах, которые помогут правильно проанализировать такие ряды.