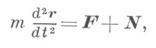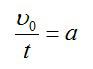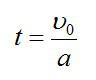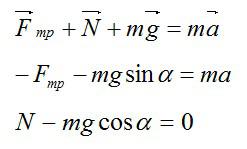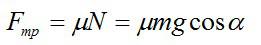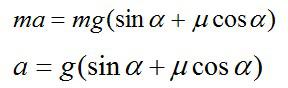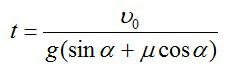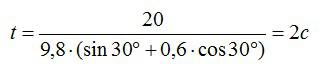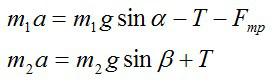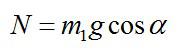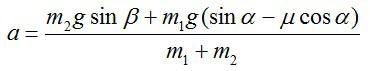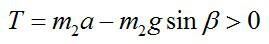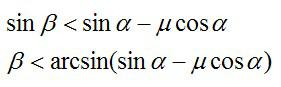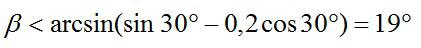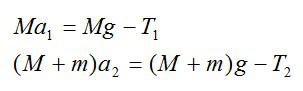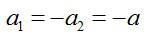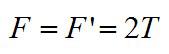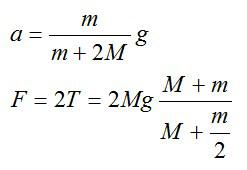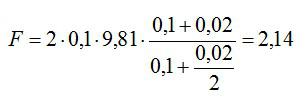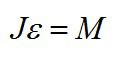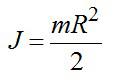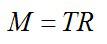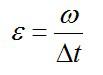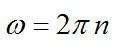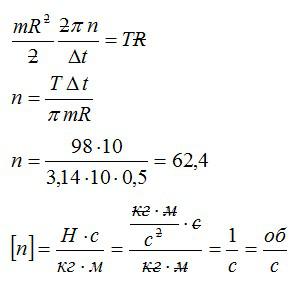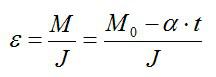Что такое динамика в математике
ДИНАМИКА
— раздел механики, в к-ром изучается движение материальных тел, происходящее под действием приложенных к ним сил, вызывающих или изменяющих это движение,- так называемых ускоряющих сил.
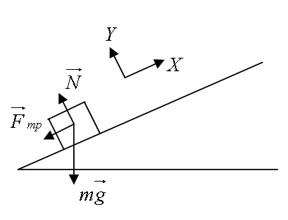
Основы Д. заложены в нач. 17 в. Г. Галилеем (G. Galilei), к-рый первый рассмотрел движение тел под действием силы тяжести и установил закон инерции. Основные принципы Д. были четко сформулированы И. Ньютоном (I. Newton) в виде трех основных законов механики и следствий из них. Дальнейшее развитие и совершенствование законов Д. содержится в трудах Л. Эйлера (L. Euler), Ж. Д’Аламбера (J. D’Alembert), Ж. Лагранжа (J. Lagrange), где были даны общие методы составления уравнений Д. Начало аналитич. методам исследования уравнений Д. положили Ж. Лагранж, У. Гамильтон Д., основывающаяся на принципах Г. Галилея и И. Ньютона, наз. классической или ньютоновской Д., в отличие от направлений, исходящих из иных принципов (квантовая механика, релятивистская Д. и др.). Классич. Д. состоит из совокупности математич. выводов и заключений, являющихся следствиями основных законов Галилея и Ньютона. В ней аксиоматически вводятся понятия неподвижного пространства (абсолютной неподвижной системы отсчета или инерциальной системы отсчета) и абсолютного времени, одинакового для всех точек пространства. Абсолютному пространству приписываются геометрич. свойства евклидова пространства. Законы Ньютона формулируются по отношению к абсолютному пространству и абсолютному времени. Они остаются справедливыми по отношению к инерциальным системам отсчета. Заключения о движении материальных тел Д. получает с помощью построения моделей (материальной точки, абсолютно твердого тела, континуума и др.). По характеру решаемых задач Д. может быть разделена на Д. материальной точки и Д. системы материальных точек. Понятие материальной точки является основным понятием классической Д. Материальной точкой наз. такое тело, геометрич. размерами к-рого можно пренебрегать при изучении его движения, но к-рое обладает конечной массой. Первый и второй законы Ньютона формулируются в Д. только для одной материальной точки. Кроме материальной точки в Д. рассматривают еще модель абсолютно твердого тела, расстояния между точками к-рого не изменяются во время движения. Эти основные модели Д. позволяют успешно решать ряд конкретных задач о движении реальных тел. В Д. системы материальных точек рассматриваются движения таких тел, к-рые находятся во взаимосвязи друг с другом. Д. системы включает в себя Д. твердого тела, Д. систем с переменной массой, Д. упругого и пластически деформируемого тела, Д. жидкости и газа и др. Характер движения материальной системы определяется действующими на нее силами (активными силами), а также связями, наложенными на точки системы, действие к-рых может быть заменено действием сил реакций связи (пассивными силами). Действующие на систему материальных точек силы являются результатом взаимодействия отдельных материальных точек, как входящих, так и не входящих в рассматриваемую систему. В соответствии с этим различают силы внутренние и внешние. Силы могут быть представлены как функции положений материальных точек, их скоростей и времени. В Д. решаются две основные задачи: 1) определение силы, производящей данное движение материальной точки или системы; 2) определение движения материальной точки или системы, происходящее под действием заданных сил. Задачи Д. решаются при помощи дифференциальных уравнений движения. Для одной материальной точки эти уравнения выражают второй закон Ньютона и могут быть записаны в виде Изучением свойств уравнений движения механич. систем, обусловленных специфич. формой этих уравнений, занимается аналитич. Д. Она рассматривает общие принципы Д., вывод из этих принципов дифференциальных уравнений движения и методов их интегрирования. Методы аналитич. Д. широко применяются как для решения различных задач Д., так и в различных областях физики. Большое значение для исследования свойств движения механич. систем получили канонические Гамильтона уравнения, к-рые дают возможность сформулировать ряд эффективных методов решения задач Д. Помимо установления общих методов составления и интегрирования уравнений движения материальных тел, движущихся под действием ускоряющих сил, в Д. рассматривается ряд специальных задач: Д. твердого тела, Д. гироскопич. систем, теория колебаний механич. систем, теория устойчивости движения, теория удара и др. — раздел механики, в к-ром изучается движение материальных тел, происходящее под действием приложенных к ним сил, вызывающих или изменяющих это движение,- так называемых ускоряющих сил. Основы Д. заложены в нач. 17 в. Г. Галилеем (G. Galilei), к-рый первый рассмотрел движение тел под действием силы тяжести и установил закон инерции. Основные принципы Д. были четко сформулированы И. Ньютоном (I. Newton) в виде трех основных законов механики и следствий из них. Дальнейшее развитие и совершенствование законов Д. содержится в трудах Л. Эйлера (L. Euler), Ж. Д’Аламбера (J. D’Alembert), Ж. Лагранжа (J. Lagrange), где были даны общие методы составления уравнений Д. Начало аналитич. методам исследования уравнений Д. положили Ж. Лагранж, У. Гамильтон Д., основывающаяся на принципах Г. Галилея и И. Ньютона, наз. классической или ньютоновской Д., в отличие от направлений, исходящих из иных принципов (квантовая механика, релятивистская Д. и др.). Классич. Д. состоит из совокупности математич. выводов и заключений, являющихся следствиями основных законов Галилея и Ньютона. В ней аксиоматически вводятся понятия неподвижного пространства (абсолютной неподвижной системы отсчета или инерциальной системы отсчета) и абсолютного времени, одинакового для всех точек пространства. Абсолютному пространству приписываются геометрич. свойства евклидова пространства. Законы Ньютона формулируются по отношению к абсолютному пространству и абсолютному времени. Они остаются справедливыми по отношению к инерциальным системам отсчета. Заключения о движении материальных тел Д. получает с помощью построения моделей (материальной точки, абсолютно твердого тела, континуума и др.). По характеру решаемых задач Д. может быть разделена на Д. материальной точки и Д. системы материальных точек.Понятие материальной точки является основным понятием классической Д. Материальной точкой наз. такое тело, геометрич. размерами к-рого можно пренебрегать при изучении его движения, но к-рое обладает конечной массой. Первый и второй законы Ньютона формулируются в Д. только для одной материальной точки. Кроме материальной точки в Д. рассматривают еще модель абсолютно твердого тела, расстояния между точками к-рого не изменяются во время движения. Эти основные модели Д. позволяют успешно решать ряд конкретных задач о движении реальных тел. В Д. системы материальных точек рассматриваются движения таких тел, к-рые находятся во взаимосвязи друг с другом. Д. системы включает в себя Д. твердого тела, Д. систем с переменной массой, Д. упругого и пластически деформируемого тела, Д. жидкости и газа и др. Характер движения материальной системы определяется действующими на нее силами (активными силами), а также связями, наложенными на точки системы, действие к-рых может быть заменено действием сил реакций связи (пассивными силами). Действующие на систему материальных точек силы являются результатом взаимодействия отдельных материальных точек, как входящих, так и не входящих в рассматриваемую систему. В соответствии с этим различают силы внутренние и внешние. Силы могут быть представлены как функции положений материальных точек, их скоростей и времени. В Д. решаются две основные задачи: 1) определение силы, производящей данное движение материальной точки или системы; 2) определение движения материальной точки или системы, происходящее под действием заданных сил. Задачи Д. решаются при помощи дифференциальных уравнений движения. Для одной материальной точки эти уравнения выражают второй закон Ньютона и могут быть записаны в виде Изучением свойств уравнений движения механич. систем, обусловленных специфич. формой этих уравнений, занимается аналитич. Д. Она рассматривает общие принципы Д., вывод из этих принципов дифференциальных уравнений движения и методов их интегрирования. Методы аналитич. Д. широко применяются как для решения различных задач Д., так и в различных областях физики. Большое значение для исследования свойств движения механич. систем получили канонические Гамильтона уравнения, к-рые дают возможность сформулировать ряд эффективных методов решения задач Д. Помимо установления общих методов составления и интегрирования уравнений движения материальных тел, движущихся под действием ускоряющих сил, в Д. рассматривается ряд специальных задач: Д. твердого тела, Д. гироскопич. систем, теория колебаний механич. систем, теория устойчивости движения, теория удара и др. Содержание 1. Динамика в разных науках 2. Динамика в физике 4. Газовая динамика Динамика – это состояние движения, ход развития, изменение какого-либо явления под влиянием действующих на него факторов. Динамика в разных науках В физике В астрономии В науках о Земле Динамика подземных вод Динамика русловых потоков В биологии Популяционная динамика старения Динамика растительности (синдинамика) — процесс постепенной трансформации растительных сообществ под действием внешних и внутренних факторов. В технике Динамика машин и механизмов В музыке Динамика в музыке — совокупность понятий и нотных обозначений, связанных с оттенками громкости звучания. Динамика в физике Динамика (греч. δύναμις — сила) — раздел механики, в котором изучаются причины возникновения механического движения. Динамика оперирует такими понятиями, как масса, сила, импульс, энергия. Динамика, базирующаяся на законах Ньютона, называется классической динамикой. Классическая динамика описывает движения объектов со скоростями от долей миллиметров в секунду до километров в секунду. Однако эти методы перестают быть справедливыми для движения объектов очень малых размеров (элементарные частицы) и при движениях со скоростями, близкими к скорости света. Такие движения подчиняются другим законам. С помощью законов динамики изучается также движение сплошной среды, т. е. упруго и пластически деформируемых тел, жидкостей и газов. В результате применения методов динамики к изучению движения конкретных объектов возник ряд специальных дисциплин: небесная механика, баллистика, динамика корабля, самолёта и т. п. Основная задача динамики Прямая задача динамики: по заданным силам определить характер движения тела. Обратная задача динамики: по заданному характеру движения определить действующие на тело силы. Классическая динамика основана на трёх основных законах Ньютона: 1-й: Существуют такие системы отсчета, относительно которых поступательно движущееся тело сохраняет свою скорость постоянной, если на него не действуют другие тела или их действие скомпенсировано. 2-й: В инерциальной системе отсчета сумма всех сил, действующих на тело, равна произведению массы этого тела на векторное ускорение этого же тела (действие на тело силы, проявляется в сообщении ему ускорения). 3-й: Тела действуют друг на друга силами равными по модулю и противоположными по направлению Если при этом рассматриваются взаимодействующие материальные точки, то обе эти силы действуют вдоль прямой, их соединяющей. Это приводит к тому, что суммарный момент импульса системы состоящей из двух материальных точек в процессе взаимодействия остается неизменным. Таким образом, из второго и третьего законов Ньютона могут быть получены законы сохранения импульса и момента импульса Законы Ньютона в неинерциальных системах отсчета Существование инерциальных систем отсчета лишь постулируется первым законом Ньютона. Реальные системы отсчета, связанные, например, с Землей или с Солнцем, не обладают в полной мере свойством инерциальности в силу их кругового движения. Вообще говоря, экспериментально доказать существование ИСО невозможно, поскольку для этого необходимо наличие свободного тела (тела на которое не действуют никакие силы), а то, что тело является свободным, может быть показано лишь в ИСО. Описание же движения в неинерциальных системах отсчета, движущихся с ускорением относительно инерциальных, требует введения т. н. фиктивных сил таких как сила инерции, центробежная сила или сила Кориолиса. Ряды динамики Ряды динамики, статистические ряды, характеризующие изменение (развитие) социально-экономических явлений во времени. Например, данные о производстве электричества в СССР за период 1928—73 представляют Ряды динамики Производство электричества в СССР, млрд. кетЧч Последовательно расположенные во времени статистические данные называются уровнями Ряды динамики Они должны быть сопоставимы между собой, особенно в территориальном разрезе, по кругу охватываемых объектов, методике расчёта, критической дате, структуре. Уровни Ряды динамики могут характеризовать величину явлении за некоторые отрезки времени (интегральные Ряды динамики) или на определённую дату (моментные Ряды динамики). Анализ Ряды динамики состоит в определении скорости и интенсивности развития рассматриваемого явления, нахождении основные тенденции его развития (тренда), измерении колеблемости уровней, установлении связи с развитием др. явлений, проведении сравнительного анализа развития разных стран или районов. Для анализа Ряды динамики определяются статистические показатели: абсолютные приросты, темпы роста и прироста, средние уровни ряда, средние абсолютные приросты, средние темпы роста и прироста. Абсолютным приростом называют разность между последующим и предыдущим уровнями, а темпом роста — их отношение. Темп прироста составит разность между темпом роста и 1 (в коэффициенте) или 100%. Средний уровень ряда для интервальных рядов определяется как средняя арифметическая, а для моментных рядов — по формуле: где — средний уровень, y1. — начальный, а уп — конечный, n — число уровней. Средний абсолютный прирост определяется как частное от деления абсолютного прироста за весь период на число единиц времени в периоде. Средний темп роста вычисляется как средняя геометрическая темпов роста за отдельные отрезки времени или как корень, степень которого определяется числом периодов, а под корнем берётся темп роста за весь период. Определение тренда ведётся выравниванием статистическим. Колеблемость уровней Ряды динамики измеряется средней из квадратов отклонений фактических уровней от тренда. Для установления связи развития данного явления с другими пользуются методом корреляции Ряды динамики, отличающимся от обычного возможностью автокорреляции, авторегрессии, переменной корреляции и временного лага. Для сравнительного анализа разных стран (районов) часто используется приведение к одному основанию, состоящее в определении темпов роста для двух или более стран за одинаковые отрезки времени. Сравнительный анализ развития лучше вести с расчётом показателей на душу населения. Всесторонний анализ Ряды динамики позволяет выявить закономерности развития отражаемых в них явлений. Газовая динамика Газовая динамика, раздел гидро-аэромеханики, в котором изучается движение сжимаемых газообразных и жидких сред и их взаимодействие с твёрдыми телами. Как часть физики, Газовая динамика связана с термодинамикой и акустикой. Фундаментальную роль в формировании Газовая динамика как самостоятельной науки сыграла опубликована в 1902 работа С. А. Чаплыгина «О газовых струях». Развитые в ней методы решения газодинамических задач получили впоследствии широкое распространение и обобщение. Плодотворный метод решения задач Газовая динамика предложили в 1908 нем. учёные Л. Прандтль и Т. Майер, исследовавшие частный случай течения газа с непрерывным увеличением скорости. В 1922 в работе «Опыт гидромеханики сжимаемой жидкости» советский учёный А. А. Фридман заложил основы динамической метеорологии. В 1929 нем. учёными Л. Прандтлем и А. Буземаном был разработан эффективный численно-графический метод решения широкого класса газодинамических задач, распространённый в 1934 сов. учёным Ф. И. Франклем на более сложные случаи течения газа. Эти методы широко применяются при решении задач Газовая динамика с помощью ЭВМ. В 1921 в СССР была создана, а в 1927 оформилась как научное учреждение газодинамическая лаборатория, деятельность которой совместно с Группой изучения реактивного движения (1932) заложила основы сов. ракетной техники. Задачи газовой динамики при проектировании разнообразных аппаратов, двигателей и газовых машин состоят в определении сил давления и трения, температуры и теплового потока в любой точке поверхности тела или канала, омываемых газом, в любой момент времени. При исследовании распространения газовых струй, взрывных и ударных волн, горения и детонации методами Газовая динамика определяются давление, температура и др. параметры газа во всей области распространения. Изучение поставленных техникой сложных задач превратило современную газовою динамику в науку о движении произвольных смесей газов, которые могут содержать также твёрдые и жидкие частицы (например, выхлопные газы ракетных двигателей на жидком или твёрдом топливе), причём параметры, характеризующие состояние этих газов (давление, температура, плотность, электропроводность и др.), могут изменяться в широких пределах. Для развития совресенной газовой динамики характерно неразрывное сочетание теоретических методов, использования ЭВМ и постановки сложных аэродинамических и физических экспериментов. Теоретические представления, частично опирающиеся на экспериментальные данные, позволяют описать с помощью уравнений движение газовых смесей сложного состава, в том числе многофазных смесей при наличии физико-химических превращений. Методами прикладной математики разрабатываются эффективные способы решения этих уравнений на ЭВМ. Наконец, из экспериментальных данных определяются необходимые значения физических и химических характеристик, свойственных изучаемой среде и рассматриваемым процессам (коэффициент вязкости и теплопроводности, скорости химических реакций, времена релаксации и др.). Многие задачи, поставленные современной техникой перед газовой динамикой, пока не могут быть решены расчётно-теоретическими методами, в этих случаях широко пользуются газодинамическими экспериментами, поставленными на основе подобия теории и законов гидродинамического и аэродинамического моделирования. Газодинамические эксперименты в аэрогазодинамических лабораториях проводятся в сверхзвуковых и гиперзвуковых аэродинамических трубах, на баллистических установках, в ударных и импульсных трубах и на др. газодинамических установках специального назначения. Газодинамические исследования ведутся в тех же научных учреждениях, что и исследования по аэродинамике, а результаты их публикуются в тех же научных журналах и сборниках. Динамика – раздел механики, которому уделяется больше всего учебных часов. Уделите 5 минут на то, чтобы прочесть нашу статью и чуть больше разобраться в решении задач по динамике. Наш телеграм – место, где мы скрупулезно отбираем, фильтруем и выкладываем все, что может быть полезно современному студенту. Под лежачий камень вода не течет, подписывайтесь! Для начала, вопрос. Какой алгоритм решения задач по динамике? Собственно, алгоритм такой же, как и для любой задачи по физике. Мы уже писали об этом в памятке по решению задач. Не забываем держать под рукой полезные формулы, повторяем вопросы из теории, и можно приступать к практическим заданиям. Вопрос 1. Что изучает динамика? Ответ. Динамика – раздел механики, который изучает взаимодействия между телами. Вопрос 2. Каково основное уравнение динамики? Ответ. Основное уравнение динамики устанавливает связь между приложенной к телу силой, его массой и ускорением тела. Вопрос 3. Что такое вес тела и зависит ли он от местоположения тела на поверхности Земли? Ответ. Вес – это сила, с которой тело действует на опору. Вес зависит от ускорения свободного падения, а значит и от географического местоположения на поверхности планеты. А вот масса тела всегда неизменна (за исключением движения со скоростью, близкой к скорости света). Вопрос 4. В каких системах отсчета справедлив второй закон Ньютона? Ответ. Второй закон Ньютона справедлив в инерциальных системах отсчета. Вопрос 5. Сила тяжести на земле является отдельным проявлением одного из фундаментальных физических взаимодействий. Что это за взаимодействие. Ответ. Конечно, это гравитационное взаимодействие. А сила тяжести – проявление силы всемирного тяготения. Условие Тело находится у основания наклонной плоскости с углом при основании α = 30°. Коэффициент трения о поверхность равен µ = 0,6 и масса тела m = 2 кг. Сколько времени тело будет двигаться по наклонной плоскости, если его толкнуть вверх вдоль плоскости со скоростью υ0 = 20 м/с? (g = 9,8 м/с2). Решение Для начала, выполним рисунок: Тело будет двигаться равнозамедленно с ускорением, равным –a в течение времени t, при этом Определим ускорение a. Запишем второй закон Ньютона в векторной форме и в проекциях на оси Х и Y соответственно: Сила трения определяется выражением Следовательно, время, в течение которого тело будет двигаться по наклонной плоскости: Подставим числовые значения: Ответ: 2 секунды. Условие В изображенной на рисунке системе нижний брусок может двигаться по наклонной плоскости, составляющей с горизонтом угол α = 30, а верхний брусок – вдоль наклонной плоскости, составляющий с горизонтом некоторый угол β. Коэффициент трения между нижним бруском и наклонной плоскостью равен µ = 0,2, трение между верхним бруском и наклонной плоскостью отсутствует. Считая соединяющую бруски нить очень легкой и нерастяжимой, и пренебрегая массой блока и трением в его оси, найдите, при каких значениях угла β нить будет растянута. Решение Так как тангенс угла α больше, чем коэффициент трения между бруском и поверхностью, нижний брусок будет скользить по наклонной плоскости даже при ненатянутой нити. Следовательно, в том случае, когда оба бруска движутся и нить натянута, модули ускорений брусков будут одинаковыми. Обозначим массу нижнего бруска как m1, массу верхнего бруска как m2, а силу натяжения соединяющей их нити как T. Тогда для каждого из брусков можно записать второй закон Ньютона в проекции на направление его движения: где Fтр – действующая на нижний брусок сила трения скольжения, N – действующая на него сила нормальной реакции опоры. Решая совместно полученные уравнения, найдем: Для того, чтобы нить была натянута, должно выполняться неравенство: С учетом полученного выражения для модуля ускорения a, это неравенство можно переписать в следующем виде: Подставим числовые значения и найдем искомый угол: Ответ: 19°. Условие Два одинаковых груза массой M = 100 г каждый подвешены на концах невесомой и нерастяжимой нити, перекинутой через невесомый блок с неподвижной осью. На один из них кладут перегрузок массой m = 20 г, после чего система приходит в движение. Найдите модуль силы F, действующей на ось блока во время движения грузов. Трением пренебречь. Решение На основании второго закона Ньютона уравнение движение для обоих грузов с учетом перегрузки на одном из них в проекции на вертикальную ось, направленную вниз, выглядит следующим образом: где a1 и a2 – проекции ускорений грузов M и (M+m) на вертикальную ось; Из-за невесомости блока и нити и отсутствия трения, справедливо равенство: В силу третьего закона Ньютона: где F с индексом штрих – сила, действующая на блок со стороны его оси. Из первых двух уравнений получим: Подставим числовые значения: Ответ: 2,14 Ньютона. Кстати! Для наших читателей действует скидка 10% на любой вид работы. Условие Маховик радиусом R=0,5 м и массой 10 кг соединен с мотором при помощи приводного ремня. Натяжение ремня, идущего без скольжения, постоянно и равно Т=98 Н. Какое число оборотов в секунду будет делать маховик через Δt=10 с после начала движения. Маховик считать однородным диском. Решение Основное уравнение динамики вращательного движения: Момент силы натяжения ремня: Угловое ускорение маховика: Угловая скорость маховика: Решая уравнения, записанные выше, получим ответ: Ответ: 62,4 оборота в секунду Условие Момент силы, приложенный к вращающемуся телу изменяется по закону M=M0-αt. Момент остаётся постоянным в течение всего времени вращения. Зависимость углового ускорения от времени представлена на рисунке. Найти выражение для углового ускорения. Решение Согласно основному закону динамики вращательного движения: Это уравнение прямой с отрицательным углом наклона, что соответствует рисунку. Нужна помощь в решении задач по динамике, теоретической механике, деталям машин, химии, etc? Обращайтесь за ней в профессиональный студенческий сервис.ДИНАМИКА
Динамика
Содержание
Задачи по динамике с решениями
Вопросы по теме «Динамика»
Задачи по динамике поступательного движения с решениями
Задача №1. Определение времени движения
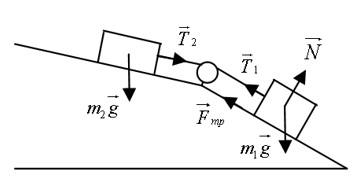
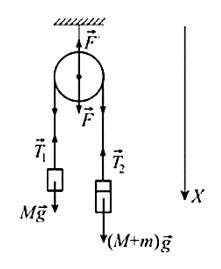
Задача №2. Применение второго закона Ньютона
Так как нижний брусок не движется в направлении, перпендикулярном плоскости, то из второго закона Ньютона следует:Задача №3. Нахождение силы
T1 и T2 – проекции сил натяжения нити на вертикальную ось. Так как нить не растяжима (по условию задачи), тоЗадачи по динамике вращательного движения с решениями
Задача №4. Нахождение числа оборотов маховика
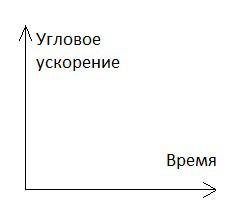
Задача №5. Нахождение углового ускорения