Что такое динамо в физике
ДИНАМО-ЭФФЕКТ
Полезное
Смотреть что такое «ДИНАМО-ЭФФЕКТ» в других словарях:
ДИНАМО-ЭФФЕКТ — ДИНАМО ЭФФЕКТ, см. Гидромагнитное динамо (см. ГИДРОМАГНИТНОЕ ДИНАМО) … Энциклопедический словарь
Магнитное динамо — Гидромагнитное (или магнитогидродинамическое, или просто МГД ) динамо (динамо эффект) эффект самогенерации магнитного поля при определённом движении проводящей жидкости. Содержание 1 Теория 2 Приложения 2.1 Ге … Википедия
гидромагнитное динамо — усиление или поддержание в стационарном состоянии магнитного поля гидродинамическим движением проводящей среды (плазмы, жидкости). Механизм гидромагнитного динамо подобен генерации электрического тока и магнитного поля в динамо машине с… … Энциклопедический словарь
Солнечное динамо — … Википедия
СОЛНЕЧНАЯ СИСТЕМА — Солнце и обращающиеся вокруг него небесные тела 9 планет, более 63 спутников, четыре системы колец у планет гигантов, десятки тысяч астероидов, несметное количество метеороидов размером от валунов до пылинок, а также миллионы комет. В… … Энциклопедия Кольера
ЗЕМНОЙ МАГНЕТИЗМ — (геомагнетизм), 1) магнитное поле Земли. 2) Раздел геофизики, изучающий распределение в пр ве и изменения во времени магн. поля Земли, а также связанные с ним физ. процессы в Земле и в атмосфере. В каждой точке пр ва геомагн. поле характеризуется … Физическая энциклопедия
МАГНИТНАЯ ГИДРОДИНАМИКА — наука о движении электропроводящих жидкостей и газов в присутствии магнитного поля; раздел физики, развившийся на стыке гидродинамики и классической электродинамики. Характерными для М. г. объектами явл. плазма (настолько, что М. г. иногда… … Физическая энциклопедия
Космическая магнитогидродинамика — раздел астрофизики, сформировавшийся в 40 х гг. 20 в., в котором методы магнитной гидродинамики (См. Магнитная гидродинамика) применяются при исследованиях космических объектов: Солнца, звёзд, межзвёздного газа, межпланетной среды,… … Большая советская энциклопедия
МАГНИТНОЕ ПОЛЕ — силовое поле, действующее на движущиеся электрич. заряды и на тела, обладающие магнитным моментом (независимо от состояния их движения). М. п. характеризуется вектором магнитной индукции В. Значение В определяет силу, действующую в данной точке… … Физическая энциклопедия
Магнитное динамо
Гидромагнитное (или магнитогидродинамическое, или просто МГД-) динамо (динамо-эффект) — эффект самогенерации магнитного поля при определённом движении проводящей жидкости.
Содержание
Теория
Теорема Каулинга доказывает, что двумерные или осесимметричные движения проводящей среды не могут вызвать постоянный рост магнитного поля. Эта и другие «антидинамо-теоремы» долгое время сдерживали попытки найти работающий пример самогенерации магнитного поля.
Первой конфигурацией, показывающей возможность генерации магнитного поля при специальном движении проводящей среды, было динамо Пономаренко (1978). После этого было исследовано несколько примеров конфигураций, допускающих такую возможность (в частности, ABC-динамо, динамо Ричардсона и др.)
Приложения
Магнитное поле в любой проводящей (но не сверхпроводящей) среде со временем быстро затухает и даже если во время своего образования астрономические объекты (галактики, звёзды, планеты) имели какое-то магнитное поле, то к настоящему времени его бы уже нельзя было зарегистрировать. Тем не менее у большинства объектов магнитное поле существует. Одной из теорий, объясняющей поддержание амплитуды магнитного поля, может быть теория динамо.
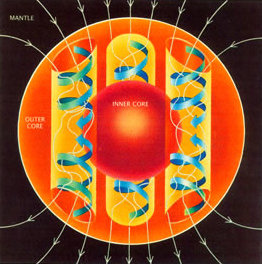
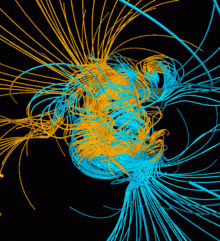
Геодинамо
Поскольку во время инверсии магнитное поле практически отсутствует, на Землю обрушится ливень заряженных частиц, основная доля которых приходится на поток, испускаемый Солнцем. По палеомагнитным данным, в прошлом такие инверсии происходили через некоторые (случайные) промежутки времени. Каким образом это влияет на биосферу Земли (и влияет ли вообще) на сегодняшний день — неизвестно.
Солнечное динамо
Предполагается, что магнитное динамо ответственно за существование магнитного поля Солнца, которое проявляется, в частности, в образовании солнечных пятен.
В физика, то теория динамо предлагает механизм, с помощью которого небесное тело, такое как земной шар или звезда генерирует магнитное поле. Теория динамо описывает процесс, посредством которого вращающийся, конвекция, и электрически проводящая жидкость может поддерживать магнитное поле более астрономический шкалы времени. Считается, что динамо-машина является источником Магнитное поле Земли и магнитные поля Меркурия и Планеты-гиганты.
Содержание
История теории
Когда Уильям Гилберт опубликовано де Магнет в 1600 году он пришел к выводу, что Земля является магнитной, и предложил первую гипотезу происхождения этого магнетизма: постоянный магнетизм, подобный тому, что обнаружен в магнит. В 1919 г. Джозеф Лармор предложил, чтобы динамо может генерировать поле. [2] [3] Однако даже после того, как он выдвинул свою гипотезу, некоторые выдающиеся ученые предложили альтернативные объяснения. Эйнштейн считал, что может быть асимметрия между обвинениями электрон и протон таким образом Магнитное поле Земли будет производить вся Земля. В Нобелевская премия победитель Патрик Блэкетт провели серию экспериментов, ищущих фундаментальную связь между угловой момент и магнитный момент, но не нашел. [4] [5]
Уолтер М. Эльзассер, который считается «отцом» принятой в настоящее время теории динамо как объяснения магнетизма Земли, предположил, что это магнитное поле является результатом электрических токов, индуцированных в жидком внешнем ядре Земли. Он раскрыл историю магнитного поля Земли, первооткрывателя исследования магнитной ориентации минералов в горных породах.
Чтобы поддерживать магнитное поле против омический распада (который произошел бы для поля диполя через 20 000 лет), внешнее ядро должно быть конвектирующим. В конвекция вероятно, некоторая комбинация тепловой и композиционной конвекции. Мантия контролирует скорость отвода тепла от ядра. Источники тепла включают гравитационную энергию, выделяемую при сжатии ядра, гравитационную энергию, выделяемую при отклонении легких элементов (вероятно, сера, кислород, или же кремний) на внутренней границе ядра по мере его роста, скрытая теплота кристаллизации на внутренней границе ядра и радиоактивность калий, уран и торий. [6]
На заре 21-го века численное моделирование магнитного поля Земли не было успешно продемонстрировано, но, похоже, стало возможным. Первоначальные модели сосредоточены на генерации поля за счет конвекции во внешнем жидком ядре планеты. Можно было продемонстрировать генерацию сильного поля, подобного Земле, когда модель предполагала однородную температуру поверхности ядра и исключительно высокую вязкость жидкости ядра. Расчеты, которые включали более реалистичные значения параметров, дали магнитные поля, которые были менее похожи на земные, но также указали путь для уточнения модели, которая в конечном итоге может привести к точной аналитической модели. Незначительные изменения температуры поверхности ядра, в диапазоне нескольких милликельвинов, приводят к значительному увеличению конвективного потока и создают более реалистичные магнитные поля. [7] [8]
Формальное определение
Когда-то считалось, что диполь, который включает большую часть Магнитное поле Земли и смещен по оси вращения на 11,3 градуса, был вызван постоянной намагниченностью материалов в земле. Это означает, что теория динамо первоначально использовалась для объяснения магнитного поля Солнца во взаимосвязи с магнитным полем Земли. Однако эта гипотеза, первоначально предложенная Джозеф Лармор в 1919 г. был модифицирован благодаря обширным исследованиям магнитных светская вариация, палеомагнетизм (включая изменение полярности), сейсмологии и обилия элементов в Солнечной системе. Также применение теорий Карл Фридрих Гаусс Магнитные наблюдения показали, что магнитное поле Земли имело внутреннее, а не внешнее происхождение.
Для работы динамо-машины необходимы три условия:
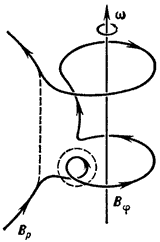
В случае с Землей магнитное поле создается и постоянно поддерживается конвекцией жидкого железа во внешнем ядре. Необходимым условием индукции поля является вращающаяся жидкость. Вращение внешнего сердечника обеспечивается Эффект Кориолиса вызвано вращением Земли. Сила Кориолиса имеет тенденцию организовывать движения жидкости и электрические токи в столбцы (см. Также Колонны Тейлора) совмещен с осью вращения. Индукция или создание магнитного поля описывается уравнение индукции:
∂ B ∂ т = η ∇ 2 B + ∇ × ( ты × B ) < displaystyle < frac < partial mathbf > < partial t>> = eta nabla ^ <2>mathbf + nabla times ( mathbf times mathbf )>
Приливное отопление, поддерживающее динамо-машину
Приливные силы между небесными телами вызывают трение, которое нагревает их внутренности. Это называется приливным нагревом, и оно помогает поддерживать внутреннее состояние в жидком состоянии. Для производства динамо-машины требуется внутренняя жидкость, которая может проводить электричество. Энцелад Сатурна и Ио Юпитера обладают достаточным приливным нагревом, чтобы сжижать свои внутренние ядра, но они не могут создать динамо-машину, потому что не могут проводить электричество. [11] [12] У Меркурия, несмотря на свой небольшой размер, есть магнитное поле, потому что у него есть проводящее жидкое ядро, созданное его составом из железа и трением, возникающим в результате его сильно эллиптической орбиты. [13] Предполагается, что у Луны когда-то было магнитное поле, основанное на данных, полученных от намагниченных лунных горных пород, из-за ее кратковременного более близкого расстояния к Земле, вызывающего приливный нагрев. [14] Орбита и вращение планеты помогают создать жидкое ядро и дополняют кинетическую энергию, которая поддерживает действие динамо.
Кинематическая теория динамо
В кинематической теории динамо поле скорости предписано, а не является динамической переменной. Этот метод не может обеспечить изменение во времени поведения полностью нелинейного хаотического динамо, но полезен при изучении того, как напряженность магнитного поля изменяется в зависимости от структуры и скорости потока.
С помощью Уравнения Максвелла одновременно с завитком Закон Ома, можно вывести то, что по сути является линейным уравнением собственных значений для магнитных полей (B), что можно сделать, если предположить, что магнитное поле не зависит от поля скорости. Приходит критический магнитное число Рейнольдса выше которого сила потока достаточна для усиления наложенного магнитного поля, а ниже которого она затухает.
Наиболее функциональная особенность кинематической теории динамо состоит в том, что ее можно использовать для проверки того, способно ли поле скоростей к действию динамо. Применяя определенное поле скорости к небольшому магнитному полю, можно определить путем наблюдения, имеет ли магнитное поле тенденцию к увеличению или нет в ответ на приложенный поток. Если магнитное поле действительно растет, то система либо способна к действию динамо, либо является динамо, но если магнитное поле не растет, то это просто называется нединамо.
В мембранная парадигма это способ взглянуть на черные дыры что позволяет выразить материал вблизи их поверхностей на языке теории динамо.
Как спонтанное нарушение топологической суперсимметрии
Нелинейная теория динамо
Численные модели используются для моделирования полностью нелинейных динамо. Используются следующие уравнения:
Затем эти уравнения безразмерны, вводятся безразмерные параметры,
куда Ра это Число Рэлея, E в Число Экмана, Pr и Вечера в Прандтль и магнитное число Прандтля. Масштабирование магнитного поля часто бывает Число Эльзассера единицы B = ( ρ Ω / σ ) 1 / 2 < Displaystyle B = ( rho Omega / sigma) ^ <1/2>> 
Преобразование энергии между магнитной и кинематической энергией
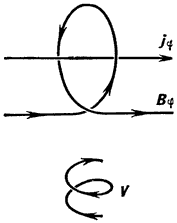
Из диаграммы выше не ясно, почему этот член должен быть положительным. Простой аргумент может быть основан на рассмотрении чистых эффектов. Чтобы создать магнитное поле, чистый электрический ток должен обернуться вокруг оси вращения планеты. В этом случае, чтобы член был положительным, чистый поток проводящего вещества должен быть направлен к оси вращения. На диаграмме показан только чистый поток от полюсов к экватору. Однако сохранение массы требует дополнительного потока от экватора к полюсам. Если бы этот поток был вдоль оси вращения, это означает, что циркуляция будет завершена потоком от показанных к оси вращения, производя желаемый эффект.
Порядок величины магнитного поля, создаваемого динамо Земли
Из них гравитационная сила и центробежная сила находятся консервативный и поэтому не имеют общего вклада в движение жидкости в замкнутых контурах. Число Экмана (определенное выше), которое представляет собой соотношение между двумя оставшимися силами, а именно вязкостью и силой Кориолиса, очень мало внутри внешнего ядра Земли, потому что его вязкость мала (1,2-1,5 × 10 −2 паскаль-секунда [19] ) за счет своей ликвидности.
Плотность тока J сам по себе является результатом магнитного поля согласно Закон Ома. Опять же, из-за движения материи и потока тока, это не обязательно поле в одном и том же месте и времени. Однако эти соотношения все еще можно использовать для определения порядков величин, о которых идет речь.
Обратите внимание, что направление магнитного поля не может быть выведено из этого приближения (по крайней мере, не его знак), поскольку оно выглядит в квадрате, и, действительно, иногда перевернутый, хотя в целом он лежит на той же оси, что и Ω < displaystyle mathbf < Omega>> 
Магнитное поле магнитный диполь имеет обратную кубическую зависимость от расстояния, поэтому его порядок величины на поверхности земли можно аппроксимировать, умножив полученный выше результат на (рвнешнее ядро/рземной шар) 3 = (2890/6370) 3 = 0,093, что дает 2,5х10 −5 Тесла, недалеко от измеренного значения 3х10 −5 Тесла в экватор.
Численные модели
В широком смысле модели геодинамо пытаются создать магнитные поля, согласующиеся с данными наблюдений, при определенных условиях и уравнениях, как упоминалось в разделах выше. Реализация магнитогидродинамический Уравнения успешно имели особое значение, потому что они подтолкнули модели динамо к самосогласованности. Хотя модели геодинамо особенно распространены, модели динамо не обязательно ограничиваются геодинамо; Также представляют интерес модели солнечного и общего динамо. Изучение моделей динамо полезно в области геофизики, так как с его помощью можно определить, как различные механизмы формируют магнитные поля, подобные тем, которые создаются астрофизическими телами, такими как Земля, и как они заставляют магнитные поля проявлять определенные особенности, такие как изменение полярности.
Уравнения, используемые в численных моделях динамо, очень сложны. В течение десятилетий теоретики были ограничены двумерным кинематическая динамо описанные выше модели, в которых движение жидкости выбирается заранее и рассчитывается влияние на магнитное поле. Прогресс от линейных к нелинейным трехмерным моделям динамо в значительной степени сдерживался поиском решений уравнений магнитогидродинамики, которые устраняют необходимость во многих предположениях, сделанных в кинематических моделях, и допускают самосогласованность.
Первый самосогласованный Модели динамо, которые определяют как движение жидкости, так и магнитное поле, были разработаны двумя группами в 1995 году, одна в Японии. [21] и один в Соединенных Штатах. [22] [23] Последний был создан в качестве модели для геодинамо и получил значительное внимание, поскольку успешно воспроизводил некоторые характеристики поля Земли. [18] После этого прорыва произошел большой скачок в разработке разумных трехмерных моделей динамо. [18]
Хотя сейчас существует множество самосогласованных моделей, между ними есть существенные различия как в результатах, которые они дают, так и в способах их разработки. [18] Учитывая сложность разработки модели геодинамо, есть много мест, где могут возникнуть расхождения, например, при принятии предположений, касающихся механизмов, обеспечивающих энергию для динамо, при выборе значений параметров, используемых в уравнениях, или при нормализации уравнений. Несмотря на множество различий, которые могут возникнуть, у большинства моделей есть общие черты, такие как четкие осевые диполи. Во многих из этих моделей такие явления, как светская вариация и инверсия геомагнитной полярности также были успешно воссозданы. [18]
Наблюдения
Современное моделирование
Сложность моделирования динамо настолько велика, что модели геодинамо ограничены нынешней мощностью суперкомпьютеров, особенно потому, что вычисление Экман и Рэлей Количество внешнего ядра чрезвычайно сложно и требует огромного количества вычислений.
После прорыва самосогласования в 1995 г. было предложено множество улучшений в моделировании динамо. Одно из предложений при изучении сложных изменений магнитного поля заключается в применении спектральные методы для упрощения вычислений. [24] В конечном счете, до тех пор, пока не будет достигнута значительная мощность компьютеров, методы расчета реалистичных моделей динамо должны быть сделаны более эффективными, поэтому усовершенствование методов расчета модели имеет большое значение для развития численного моделирования динамо.
Что такое динамо в физике
Большинство космич. тел (планеты, звёзды, галактики) и окружающая их среда обладают магн. полями. Происхождение и наблюдаемые изменения космич. магн. полей связаны, как правило, с движениями плазмы. Идею о том, что движения плазмы могут приводить к усилению магн. поля, выдвинул англ. физик Дж. Лармор в 1919 г. Название Г. д. возникло из-за схожести процесса с работой динамо-машины. Особенность Г. д. состоит в том, что оно должно быть самовозбуждающимся, т. е. не поддерживающимся за счёт внеш. источников поля. В теоретич. исследованиях принято говорить о проблеме кинематич. Г. д., к-рую можно сформулировать след. образом. Пусть в объёме плазмы с заданной проводимостью поддерживаются к.-л. движения плазмы и создано слабое магн. поле, не поддерживаемое далее внеш. источниками. Если со временем поле и полная магнитная энергия рассматриваемого объёма не убывают, несмотря на действие омической диссипации, то имеет место Г. д.
Теория Г. д. явл. ветвью магнитогидродинамики. Релятивистские эффекты, токи смещения, в теории Г. д. обычно не учитываются. В этом смысле магн. поле не зависит от системы отсчёта и можно пользоваться представлением о магн. силовых линиях.
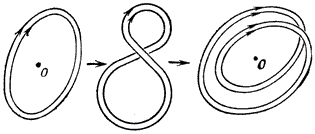
Возможность усиления начального (затравочного) магн. поля движениями среды связана с т. н. вмороженностью поля в плазму (см. Магнитогидродинамика ). Дело в том, что характерные размеры L областей, занимаемых космич. телами, обычно столь велики, что даже при умеренной проводимости плазмы s характерные времена t омического затухания поля огромны:
t = 4 ps L 2 /c 2 є L 2 /vm,
10 8 ), принципиально важно ответить на вопрос, существует ли быстрое динамо со скоростью роста, не стремящейся к нулю (или к отрицат. значению) при Rm >> 1.