Что такое дипольный момент

ДИПОЛЬНЫЙ МОМЕНТ

Полезное

Смотреть что такое «ДИПОЛЬНЫЙ МОМЕНТ» в других словарях:

ДИПОЛЬНЫЙ МОМЕНТ — физическая величина, характеризующая свойства диполя. Электрический дипольный момент равен произведению положительного заряда электрического диполя на расстояние между зарядами и направлен от отрицательного заряда к положительному. Магнитный… … Большой Энциклопедический словарь

Дипольный момент — Классическая электродинамика Магнитное поле соленоида Электричество · Магнетизм Электростатика Закон Кулона … Википедия

дипольный момент — физическая величина, характеризующая свойства диполя. Электрический дипольный момент равен произведению положительного заряда электрического диполя на расстояние между зарядами и направлен от отрицательного заряда к положительному. Магнитный… … Энциклопедический словарь

дипольный момент — постоянный электрический момент частицы; дипольный момент; отрасл. постоянный дипольный момент Электрический момент частицы (молекулы или комплекса молекул) при отсутствии внешнего электрического поля … Политехнический терминологический толковый словарь

дипольный момент — dipolinis momentas statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. dipole moment vok. Dipolmoment, n rus. дипольный момент, m pranc. moment de dipôle, m; moment… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

дипольный момент — dipolinis momentas statusas T sritis chemija apibrėžtis Vektorinis dydis, lygus bet kurio dipolio elektros krūvio ir atstumo tarp polių sandaugai. atitikmenys: angl. dipole moment rus. дипольный момент ryšiai: sinonimas – elektrinio dipolio… … Chemijos terminų aiškinamasis žodynas

дипольный момент — dipolinis momentas statusas T sritis fizika atitikmenys: angl. dipole moment vok. Dipolmoment, n rus. дипольный момент, m pranc. moment dipolaire, m … Fizikos terminų žodynas

Дипольный момент — электрический, физическая величина, характеризующая электрические свойства системы заряженных частиц. Д. м. системы из N заряженных частиц равен где ei заряд частицы номера i, а ri её радиус вектор. Д. м. нейтральной в… … Большая советская энциклопедия

ДИПОЛЬНЫЙ МОМЕНТ — физ. величина, характеризующая свойства диполя. Электрич. Д. м. равен произведению положит. заряда электрич. диполя на расстояние между зарядами и направлен от отрицат. заряда к положительному. Магн. Д. м. контура с током пропорционален… … Естествознание. Энциклопедический словарь

Источник

Метод отталкивания локализованных электронных пар валентной оболочки центрального атома (метод Гиллеспи); дипольный момент молекулы

Материалы портала onx.distant.ru

Основные положения метода

Обозначения, используемые в методе Гиллеспи

А – центральный атом;

X – лиганд, с которым центральный атом образует химическую связь, то есть даёт связывающие электронные пары;

Е – неподелённая электронная пара;

n, m – соответственно число связывающих и неподелённых электронных пар.

Алгоритм определения строения молекул по методу Гиллеспи

Для того, чтобы определить строение молекулы методом Гиллеспи, предлагается следующий порядок действий.

(n + m) = 1/2 (N_ц + N_л – z ) – π (1)

N_ц – число электронов центрального атома на его внешнем электронном слое,

N_л – число электронов лигандов, участвующих в образовании связей с центральным атомом,

π – число π-связей в молекуле,

z – заряд иона (в случае определения строения молекулярного аниона).

В табл. 1. обобщаются возможные варианты использования метода Гиллеспи для определения строения различных молекул.

Таблица 1. Геометрия молекул неорганических и органических веществ.

№	Тип молекулы	Примеры	Общее число связывающих и неподелённых электронных пар	Пространственное расположение электронных пар	Число связывающих электронных пар	Геометрия молекулы
1	AX₂E₀	BeCl₂, CO₂	2	линейное	2	линейная
2	AX₃E₀	BF₃, SO₃	3	правильный треугольник	3	правильный треугольник
3	AX₂E₁	SnCl₂ SO₂	3	правильный треугольник	2	угловая
4	AX₄E₀	CH₄, CCl₄	4	тетраэдр	4	тетраэдр
5	AX₃E₁	NH₃, PH₃	4	тетраэдр	3	треугольная пирамида
6	AX₂E₂	H₂O	4	тетраэдр	2	угловая
7	AX₅E₀	PCl₅	5	тригональная бипирамида	5	тригональная бипирамида
8	AX₄E₁	SF₄	5	тригональная бипирамида	4	“качели”
9	AX₃E₂	ClF₃	5	тригональная бипирамида	3	“Т-образная”
10	AX₂E₃	XeF₂	5	тригональная бипирамида	2	линейная
11	AX₆E₀	SF₆	6	октаэдр	6	октаэдр
12	AX₅E₁	ICl₅	6	октаэдр	5	квадратная пирамида
13	AX₄E₂	XeF₄	6	октаэдр	4	плоская
14	A + X₄E₀	NH₄ +	4	тетраэдр	4	тетраэдр
15	AX₄ 2- E₀	SO₄ 2-	4	тетраэдр	4	тетраэдр
16	AX₃ 2- E₁	SO₃ 2-	4	тетраэдр	3	треугольная пирамида
17	A — X₆E₀	PCl₆ —	6	октаэдр	6	октаэдр
18	AX’₁X»₂E₀	COCl₂	3	правильный треугольник	3	правильный треугольник

Дипольный момент молекулы

Мера полярности связи – её дипольный момент (μ) – определяется произведением:

μ = ql

где q – эффективный заряд, l – длина диполя (расстояние между двумя равными по величине и противоположными по знаку зарядами +q и –q).

Дипольный момент – это векторная величина. Понятия “дипольный момент связи” и “дипольный момент молекулы” совпадают только для двухатомных молекул. Дипольный момент сложной молекулы равен векторной сумме дипольных моментов всех связей. Дипольный момент многоатомной молекулы зависит не только от полярности отдельных связей в молекуле, но и от геометрической формы молекулы.

Рис. 1. Дипольные моменты молекул СО₂ и Н₂О

Примеры определения строения молекул по методу Гиллеспи

Пример 1. Молекула BF₃.

n + m = (4 + 2)/2 = 3

(у олова на внешнем слое четыре электрона и два электрона дают атомы хлора; π-связи в молекуле отсутствуют).

Пример 3. Молекула XeF₄.

(у атома Хе восемь электронов на внешнем электронном слое и два электрона дают атомы F; π-связи в молекуле отсутствуют).

Пример 4. Молекула SO₂.

(у атома серы на внешнем электронном слое шесть электронов, четыре электрона дают два атома кислорода; в молекуле две π-связи которые вычитаются при определении n+m).

Атом серы имеет шесть валентных электронов. Из них четыре идут на образование π- и σ-связей с двумя атомами кислорода (О= S= O). В результате, у атома серы остается одна неподелённая пара электронов.

Строение карбонат-иона – плоский треугольник.

Задачи для самостоятельного решения

1. Из приведенных молекул полярными являются:

Источник

Дипольный момент

Смотреть что такое «Дипольный момент» в других словарях:

ДИПОЛЬНЫЙ МОМЕНТ — электрический, векторная величина, характеризующая асимметрию распределения положит. и отрицат. зарядов в электрически нейтральной системе. Два одинаковых по величине заряда +q и Чq образуют электрич. диполь с Д. м. m = q l, где l расстояние… … Химическая энциклопедия

Источник

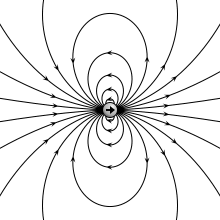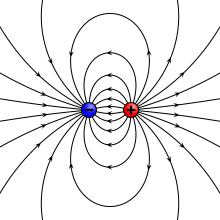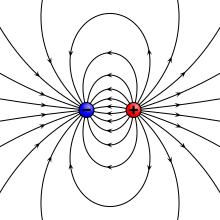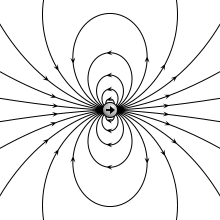
Теоретически электрический диполь определяется членом первого порядка мультипольного разложения ; он состоит из двух равных и противоположных зарядов, бесконечно близких друг к другу, хотя реальные диполи имеют разделенный заряд.

СОДЕРЖАНИЕ

Элементарное определение

и направлена от отрицательного заряда к положительному. Некоторые авторы могут разделить d пополам и использовать s = d / 2, поскольку эта величина представляет собой расстояние между любым зарядом и центром диполя, что приводит к коэффициенту два в определении.

Энергия и крутящий момент

На объект с электрическим дипольным моментом действует крутящий момент τ, когда он помещен во внешнее электрическое поле. Крутящий момент стремится выровнять диполь с полем. Диполь, расположенный параллельно электрическому полю, имеет меньшую потенциальную энергию, чем диполь, находящийся с ним под некоторым углом. Для пространственно однородного электрического поля E энергия U и крутящий момент определяются выражением τ <\ displaystyle <\ boldsymbol <\ tau>>>

Диполь, ориентированный параллельно или антипараллельно направлению увеличения неоднородного электрического поля (градиент поля), будет испытывать крутящий момент, а также силу в направлении своего дипольного момента. Можно показать, что эта сила всегда будет параллельна дипольному моменту независимо от со- или антипараллельной ориентации диполя.

Выражение (общий случай)

Это выражение эквивалентно предыдущему выражению в случае нейтральности заряда и N = 2. Для двух противоположных зарядов, обозначая расположение положительного заряда пары как r ₊ и расположение отрицательного заряда как r _— :

показывая, что вектор дипольного момента направлен от отрицательного заряда к положительному, поскольку вектор положения точки направлен наружу от начала координат к этой точке.

Дипольный момент особенно полезен в контексте общей нейтральной системы зарядов, например пары противоположных зарядов или нейтрального проводника в однородном электрическом поле. Для такой системы зарядов, представленной в виде массива пар противоположных зарядов, соотношение для электрического дипольного момента будет следующим:

Потенциал и поле электрического диполя.

Идеальный диполь состоит из двух противоположных зарядов с бесконечно малым разделением. Мы вычисляем потенциал и поле такого идеального диполя, начиная с двух противоположных зарядов на расстоянии d> 0 и принимая предел при d → 0.

Два близко расположенных противоположных заряда ± q имеют потенциал вида:

где разделение зарядов:

Результат для дипольного потенциала также может быть выражен как:

который связывает дипольный потенциал с точечным зарядом. Ключевым моментом является то, что потенциал диполя падает быстрее с расстоянием R, чем потенциал точечного заряда.

Электрическое поле диполя представляет собой отрицательный градиент потенциала, приводящий к:

Таким образом, хотя два близко расположенных противоположных заряда не совсем идеальный электрический диполь (потому что их потенциал на коротких расстояниях не диполь), на расстояниях, намного больших, чем их разделение, их дипольный момент p появляется непосредственно в их потенциале и поле.

Плотность дипольного момента и плотность поляризации

Дипольный момент множества зарядов,

определяет степень полярности массива, но для нейтрального массива это просто свойство вектора массива без информации об абсолютном расположении массива. Дипольный момент плотность массива р ( г ) содержит как местоположение массива и его дипольный момент. Когда приходит время вычислить электрическое поле в некоторой области, содержащей массив, уравнения Максвелла решаются, и информация о массиве зарядов содержится в плотности поляризации P ( r ) уравнений Максвелла. В зависимости от того, насколько детально требуется оценка электрического поля, более или менее информация о массиве зарядов должна быть выражена через P ( r ). Как поясняется ниже, иногда достаточно точно взять P ( r ) = p ( r ). Иногда требуется более подробное описание (например, дополнение плотности дипольного момента дополнительной квадрупольной плотностью), а иногда даже более сложные версии P ( r ).

Формулировка уравнений Максвелла, основанная на разделении зарядов и токов на «свободные» и «связанные» заряды и токи, приводит к введению D- и P- полей:

с ρ _b в качестве связанного заряда, под которым понимается разница между полной и свободной плотностями заряда.

Кстати, в отсутствие магнитных эффектов уравнения Максвелла указывают, что

Предположим, что заряды делятся на свободные и связанные, а потенциал делится на

Далее обсуждается, как несколько различных описаний дипольного момента среды связаны с поляризацией, входящей в уравнения Максвелла.

Среда с зарядовой и дипольной плотностями

Как описано ниже, модель для плотности поляризационного момента p ( r ) приводит к поляризационному

ограничен той же моделью. Для плавно изменяющегося распределения дипольного момента p ( r ) соответствующая плотность связанного заряда просто

В качестве первого примера, связывающего дипольный момент с поляризацией, рассмотрим среду, состоящую из непрерывной плотности заряда ρ ( r ) и непрерывного распределения дипольного момента p ( r ). Потенциал в позиции r равен:

интеграл поляризации можно преобразовать:

где объемное интегрирование распространяется только до ограничивающей поверхности и не включает эту поверхность.

Потенциал определяется общим зарядом, который, как показано выше, состоит из:

Короче говоря, плотность дипольного момента p ( r ) играет роль плотности поляризации P для этой среды. Обратите внимание, что p ( r ) имеет ненулевую дивергенцию, равную плотности связанного заряда (смоделированной в этом приближении).

Можно отметить, что этот подход может быть расширен для включения всех мультиполей: диполя, квадруполя и т. Д. Используя соотношение:

Плотность поляризации оказывается равной:

Поверхностный заряд

Выше было отложено обсуждение первого члена в выражении для потенциала, обусловленного диполями. Интегрирование расходимости приводит к поверхностному заряду. Рисунок справа дает интуитивное представление о том, почему возникает поверхностный заряд. На рисунке показан однородный массив идентичных диполей между двумя поверхностями. Внутри головы и хвосты диполей смежны и сокращаются. Однако на ограничивающих поверхностях отмены не происходит. Вместо этого на одной поверхности головки диполя создают положительный поверхностный заряд, а на противоположной поверхности хвосты диполя создают отрицательный поверхностный заряд. Эти два противоположных поверхностных заряда создают чистое электрическое поле в направлении, противоположном направлению диполей.

Этой идее придается математическая форма с использованием приведенного выше потенциального выражения. Если не брать в расчет бесплатную плату, есть вероятность:

Используя теорему о дивергенции, член дивергенции превращается в поверхностный интеграл:

Если ограничивающая поверхность является сферой, а точка наблюдения находится в центре этой сферы, интегрирование по поверхности сферы равно нулю: положительный и отрицательный вклады поверхностного заряда в потенциал сокращаются. Однако, если точка наблюдения смещена от центра, может возникнуть чистый потенциал (в зависимости от ситуации), потому что положительные и отрицательные заряды находятся на разных расстояниях от точки наблюдения. Поле, обусловленное поверхностным зарядом, равно:

который в центре сферической ограничивающей поверхности не равен нулю ( поля отрицательных и положительных зарядов на противоположных сторонах центра складываются, потому что оба поля указывают одинаково), а вместо этого:

В частности, если ввести электрическую восприимчивость через приближение:

где E в этом случае и в дальнейшем представляет внешнее поле, индуцирующее поляризацию.

Всякий раз, когда χ ( r ) используется для моделирования скачка ступеньки на границе между двумя областями, ступенька создает слой поверхностного заряда. Например, интегрирование по нормали к ограничивающей поверхности от точки внутри одной поверхности до другой точки снаружи:

обязательно включает вклад поверхностного заряда.

Физически более реалистичное моделирование p ( r ) привело бы к быстрому падению плотности дипольного момента, но плавно до нуля на границе ограничивающей области, вместо того, чтобы делать внезапный шаг к нулевой плотности. Тогда поверхностный заряд не будет концентрироваться на бесконечно тонкой поверхности, а вместо этого, будучи дивергенцией плавно изменяющейся плотности дипольного момента, будет распределяться по тонкому, но конечному переходному слою.

Диэлектрическая сфера в однородном внешнем электрическом поле

Приведенные выше общие замечания о поверхностном заряде конкретизируются на примере диэлектрического шара в однородном электрическом поле. Обнаружено, что сфера принимает поверхностный заряд, связанный с дипольным моментом ее внутренней части.

а внутри сферы потенциал удовлетворяет уравнению Лапласа. Пропуская некоторые детали, решение внутри сферы таково:

находясь вне сферы:

Как следствие, потенциал:

который представляет собой потенциал из-за приложенного поля и, кроме того, диполя в направлении приложенного поля (направление z ) дипольного момента:

или на единицу объема:

ведущее к полю внутри сферы:

Этот пример линейного диэлектрика показывает, что рассмотрение диэлектрической проницаемости эквивалентно модели однородного дипольного момента и приводит к нулевому заряду везде, кроме поверхностного заряда на границе сферы.

Общие СМИ

Если наблюдение ограничено областями, достаточно удаленными от системы зарядов, можно сделать мультипольное разложение точной плотности поляризации. При усечении этого разложения (например, с сохранением только дипольных членов или только дипольных и квадрупольных членов и т. Д. ) Результаты предыдущего раздела восстанавливаются. В частности, усекая расширение на дипольном члене, результат неотличим от плотности поляризации, создаваемой однородным дипольным моментом, ограниченным областью заряда. Для точности этого дипольного приближения, как показано в предыдущем разделе, плотность дипольного момента p ( r ) (которая включает не только p, но и местоположение p ) служит P ( r ).

Электрические дипольные моменты элементарных частиц

Дипольные моменты молекул

Дипольные моменты можно найти в обычных молекулах, таких как вода, а также в биомолекулах, таких как белки.

ϵ знак равно 1 + k ⟨ M Tot 2 ⟩ <\ displaystyle \ epsilon = 1 + k \ left \ langle <\ mathcal > _ <\ text > ^ <2>\ right \ rangle>

Следовательно, в диэлектрическую проницаемость (и проводимость) входят оба члена. Этот подход можно обобщить для вычисления частотно-зависимой диэлектрической проницаемости.

Источник