Что такое дискретное пространство
Дискретное метрическое пространство
Дискре́тное простра́нство в общей топологии и смежных областях математики — это пространство, в котором все точки изолированы друг от друга в некотором смысле.
Содержание
Определения
Тогда 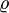
Замечание
Топология, индуцированная дискретной метрикой, является дискретной. Обратное, вообще говоря, неверно. Метрика, не являющаяся дискретной, может порождать дискретную топологию.
Примеры
Свойства
См. также
Полезное
Смотреть что такое «Дискретное метрическое пространство» в других словарях:
Дискретное топологическое пространство — Дискретное пространство в общей топологии и смежных областях математики это пространство, в котором все точки изолированы друг от друга в некотором смысле. Содержание 1 Определения 2 Замечание 3 Примеры 4 Свойства … Википедия
МЕТРИЧЕСКОЕ ПРОСТРАНСТВО — множество Xвместе с нек рой метрикойr на ном. Теоретико множественный подход к изучению фигур (пространств) основан на исследовании взаимного расположения составляющих их элементарных частей. Одной из фундаментальных характеристик взаимного… … Математическая энциклопедия
Дискретное пространство — в общей топологии и смежных областях математики это пространство, в котором все точки изолированы друг от друга в некотором смысле. Содержание 1 Определения 2 Замечание 3 Примеры … Википедия
Дискретное множество — Дискретное пространство в общей топологии и смежных областях математики это пространство, в котором все точки изолированы друг от друга в некотором смысле. Содержание 1 Определения 2 Замечание 3 Примеры 4 Свойства … Википедия
Сепарабельное пространство — (от лат. separabilis отделимый) топологическое пространство, содержащее конечное или счётное всюду плотное множество. Многие пространства, возникающие в математическом анализе и геометрии, являются сепарабельными. Сепарабельные… … Википедия
Дискретная топология — Дискретное пространство в общей топологии и смежных областях математики это пространство, в котором все точки изолированы друг от друга в некотором смысле. Содержание 1 Определения 2 Замечание 3 Примеры 4 Свойства … Википедия
Дискретная метрика — Дискретное пространство в общей топологии и смежных областях математики это пространство, в котором все точки изолированы друг от друга в некотором смысле. Содержание 1 Определения 2 Замечание 3 Примеры 4 Свойства … Википедия
Шар — Запрос «Шар» перенаправляется сюда; см. также другие значения. Шар Шар геометрическое тело; совокупность всех точек пространства, находящихся от центра на расстоянии, не больше заданного. Это расстояние называется … Википедия
Шар (метрическая геометрия) — У этого термина существуют и другие значения, см. Шар. Понятие шара в метрическом пространстве естественно обобщает понятие шара в евклидовой геометрии. Содержание 1 Определения 1.1 Замечания … Википедия
Открытый шар — Понятие шара в метрическом пространстве естественно обобщает понятие шара в евклидовой геометрии. Содержание 1 Определения 1.1 Замечания 2 Свойства 3 Примеры … Википедия
Визуализация дискретного пространства: тор против симплекса
Представим, что само понятие расстояния является искусственным и не присущим реальности. Можем ли мы себе помыслить, а еще лучше визуально представить мир без расстояний? В статье предлагается один из способов это сделать при помощи нескольких математических концепций, а именно дискретного пространства, симплекса и тора. Из обсуждения этих концепций делаются несколько выводов относительно визуализации многомерных данных.
Пространство с одинаковым расстоянием между точками
Расстояние — это мера того, насколько один объект находится ближе или дальше от другого. С идеей расстояния мы сталкиваемся в самом раннем детстве, когда пытаемся дотянутся до игрушки. Потом мы начинаем ходить и ездить, развивая способность достигать объектов, находящихся все дальше и дальше от того места, где мы находимся сейчас. Целые отрасли (транспорт, почта, телекоммуникации) построены на том, что есть некие расстояния, через которые нужно перевозить людей и грузы или передавать информацию. Различные приборы, например, бинокль, позволяют сократить расстояние хотя бы визуально.
Также расстояние может быть использовано косвенно. При визуализации данных расстояние между точками и другими объектами используется, чтобы показать отношения между другими величинами. В приборах идея «ближе-дальше» выступает как аналог «холоднее-теплее» (шкала термометра), «легче-тяжелее» (шкала весов), «медленнее-быстрее» (шкала спидометра). Мы можем измерять расстояние ради него самого, как в пути, так и чтобы понять значения каких-либо переменных.
У нас нет никаких трудностей, чтобы помыслить расстояние. Более того, это получается естественным образом.
В математике расстояние связано с понятием метрического пространства. Между любыми двумя точками (элементами, объектами) метрического пространства определено расстояние (метрика). Метрика является количественным выражением отношения «ближе-дальше», то есть, отвечает на вопрос, насколько именно ближе и насколько дальше. В геометрическом и географическом смысле метрика имеет очевидный смысл и выражается в километрах, милях и тому подобных единицах. В общем смысле метрика может иметь какой-угодно смысл, например, рейтинг участников какого-нибудь конкурса. В этом случае метрикой является количество набранных баллов, а точка отсчета — первое место.
Все эти примеры нужны были для того, чтобы показать, насколько понятие расстояния важно для нашей жизни. Можем ли мы помыслить жизнь без расстояний? С приходом интернета это стало проще в части общения, но многие другие аспекты нашей жизни все еще сильно связаны с понятием расстояния. Тем не менее, мы можем создать математическую абстракцию, в которой метрика d постоянна и равна, например, единице. Такая абстракция уже существует и называется дискретным пространством X:
В этом определении x и y — любые две точки (элементы, объекты) пространства. Определение подразумевает, что все точки находятся одинаково далеко или одинаково близко друг от друга. Взяв любую точку мы увидим, что расстояние до любой другой одинаковое. Перемещение из точки A в точку B при прочих равных занимает одинаковое количество времени. Более того, в точке B ситуация та же самая — опять расстояние до любой другой точки будет то же самое, что и до точки A.
Дискретное пространство легко представить в виде таблицы расстояний, как это делают в автомобильном атласе. На пересечении строки и столбца в такой таблице указывается расстояние для точек, соответствующих данной строке и столбцу таблицы. Согласно определению, для дискретного пространства по диагонали такой таблицы будут идти нули, все остальные же значения единицы. Пример для пространства, состоящего из шести точек от A до F:
Или с городами (в километрах):
Матрицу с абстрактными точками представить себе легко, а вот с конкретными городами уже гораздо сложнее, так как мы имеем устойчивое представление о географической карте. Как же создать визуализацию, в которой нет представления о расстоянии и отношении «ближе-дальше», базового для геометрии? Попробуем изобразить дискретное пространство, начав с одной точки и добавляя точки одну за другой на одинаковом расстоянии от всех остальных.
Визуализация дискретного пространства при помощи симплекса
Для начала представим, что наше дискретное пространство состоит всего из одной точки A. Например, это может быть какое-либо состояние системы. Так как точка всего одна, то система постоянна, всегда пребывает в состоянии, соответствующем точке A. Изображение этой точки на двумерной плоскости элементарно (рядом приведена соответствующая таблица расстояний согласно определению дискретного пространства):
В таком пространстве никакие перемещения и изменения невозможны. Можно сказать, что такое пространство соответствует постоянному значению некоторой переменной.
Добавим еще одну точку на расстоянии, равном 1. Две точки также легко изобразить на плоскости. Вместе с расстоянием между ними они образуют отрезок AB:
Теперь попробуем изобразить на плоскости еще одну точку, C. Ее мы должны разместить на расстоянии 1 от точек A и B, при этом сохранив расстояние 1 и между этими точками. Множество точек, равноудаленных от данной, это окружность. Если построить две окружности с единичным радиусом и центром в точках A и B, то пересечение этих окружностей даст множество точек, удаленных на единицу как от точки A, так и от точки B:
На рисунке одна из двух точек пересечений окружностей обозначена как C. Расстояние от точки C до точек A и B равно 1. Соединив все три точки, получим равносторонний треугольник ABC:
Таким образом, дискретное пространство из трех точек визуализируется на плоскости при помощи треугольника. Добавляем еще одну точку D. Можно ли построить эту точку так, чтобы три другие точки располагались от нее на одинаковом расстоянии, равном 1? Для этого должны выполнится два условия:
Первое условие выполняется, так как вокруг правильного треугольника можно описать окружность:
Однако, радиус описанной окружности равняется:

где a — длина стороны. Выходит, что четыре точки равноудаленные друг от друга изобразить на плоскости уже не получится. Чтобы выполнить второе условие, придется отодвинуть точку D от плоскости так, чтобы расстояния до точек A, B и C увеличилось до 1. В результате получим правильный тетраэдр, то есть, уже трехмерную фигуру в пространстве.
Если мы добавим еще одну точку в дискретное пространство, то снова столкнемся с проблемой, аналогичной добавлению четвертой точки к треугольнику. Теперь нам нужно будет построить единичную сферу, на которой лежат четыре точки A, B, C и D, в центр которой поместить точку E. Сферу описать вокруг правильного тетраэдра получится, но ее радиус будет отличаться от единицы:
Фигура, в которой пять точек равноудалены друг от друга, называется пятиячейником (пентахором). Это уже четырехмерная фигура, трехмерная проекция которой выглядит следующим образом (слева диаграмма Шлегеля, справа стереографическая проекция, Wikipedia):
Обобщением всех построенных нами фигур, начиная с точки, является n-симплекс — простейший n-мерный многогранник с n+1 вершин:
Первые три симплекса визуализируются на плоскости как есть. Тетраэдр можно спроецировать на плоскость или сделать его 3D-модель без искажений. Пентахор можно спроецировать на плоскость с сохранением комбинаторных свойств или сделать 3D-модель с искажениями. 6-симплекс и симплексы большей размерности можно представлять в виде плоских проекций, сохраняющих комбинаторные свойства, но большей наглядности достигнуть уже не получится.
Таким образом, непосредственная визуализация дискретного пространства с большим количеством точек в двух-трех измерениях, которыми ограничена наша визуализация, затруднена. Попробуем все-таки найти какой-нибудь вариант изображения дискретного пространства с сохранением его существенных свойств хоть в каком-нибудь объеме.
Тор как 3D-визуализация дискретного пространства
До сих пор мы рассматривали визуализацию дискретного пространства как бы со стороны, представляя все точки пространства перед нами, например, на экране компьютера. При этом добились наглядности при визуализации пространства, максимум из 4-5 точек. А что если поместить наблюдателя в одну из точек пространства, например в точку A? Тогда все остальные точки, сколько бы их ни было, будут равноудалены от выбранной точки и будут располагаться на окружности единичного радиуса:
Если точек дискретного пространства бесконечно много, то их визуализация из любой выбранной точки этого пространства будет представлять собой окружность. Мы обнаружили интересную особенность дискретного пространства. Если мы находимся вне его, то чтобы его представить нужно N — 1 измерений (N — количество точек). Но как только мы оказываемся внутри дискретного пространства, то можно построить его визуализацию в двух измерениях, и эта визуализация — единичная окружность.
Аналогичная окружность строится для любой другой точки дискретного пространства. Если это сделать, по-прежнему находясь в точке A, и представляя еще одного наблюдателя в других точках, то получим следующую картину:
Все окружности, построенные из точек B, C и так далее, пересекаются в точке A. То есть, визуализация дискретного пространства для наблюдателей в этих точках включает в себя эту точку A.
Однако, полученная нами визуализация не очень наглядна при большом количестве точек. Задействуем третье измерение — повернем все окружности, за исключением исходной, на 90 градусов следующим образом (точка A размещена в начале координат):
В результате мы получаем получим закрытый (самосоприкасающийся) тор в качестве 3D-визуализации дискретного пространства:
Полученная визуализация подразумевает, что наблюдатель находится в одной из точек этого пространства и представляет себе наблюдателей, находящихся в других точках пространства. Также визуализация дискретного пространства при помощи тора учитывает только отношения между точкой, в которой находится наблюдатель, и другими точками, но не между произвольными точками.
Дискретное пространство
Дискре́тное простра́нство в общей топологии и смежных областях математики — это пространство, в котором все точки изолированы друг от друга в некотором смысле.
Содержание
Определения
Тогда 
Замечание
Топология, индуцированная дискретной метрикой, является дискретной. Обратное — неверно. Метрика, не являющаяся дискретной, может порождать дискретную топологию.
Примеры
Свойства
См. также
Полезное
Смотреть что такое «Дискретное пространство» в других словарях:
ДИСКРЕТНОЕ ПРОСТРАНСТВО — пространство, наделенное дискретной топологией. С … Математическая энциклопедия
ДИСКРЕТНОЕ ПРОСТРАНСТВО-ВРЕМЯ — одна из гипотез возможной структуры пространства в микромире, характеризуемая представлением об элементарных попарно несвязных компонентах пространства, точки к рых не разделяются наблюдаемыми величинами. Приемлемой формализацией Д. п. в. могут… … Математическая энциклопедия
ПРОСТРАНСТВО И ВРЕМЯ — всеобщие формы бытия материи, её важнейшие атрибуты. В мире нет материи, не обладающей пространственно временными свойствами, как не существует П. и в. самих по себе, вне материи или независимо от неё. Пространство есть форма бытия… … Философская энциклопедия
Пространство элементарных событий — Пространство элементарных событий множество всех различных исходов случайного эксперимента. Элемент этого множества называется элементарным событием или исходом. Пространство элементарных событий называется дискретным, если число его… … Википедия
Дискретное косинусное преобразование — (англ. Discrete Cosine Transform, DCT) одно из ортогональных преобразований. Вариант косинусного преобразования для вектора действительных чисел. Применяется в алгоритмах сжатия информации с потерями, например, MPEG и JPEG. Это… … Википедия
Дискретное метрическое пространство — Дискретное пространство в общей топологии и смежных областях математики это пространство, в котором все точки изолированы друг от друга в некотором смысле. Содержание 1 Определения 2 Замечание 3 Примеры 4 Свойства … Википедия
Дискретное топологическое пространство — Дискретное пространство в общей топологии и смежных областях математики это пространство, в котором все точки изолированы друг от друга в некотором смысле. Содержание 1 Определения 2 Замечание 3 Примеры 4 Свойства … Википедия
Дискретное множество — Дискретное пространство в общей топологии и смежных областях математики это пространство, в котором все точки изолированы друг от друга в некотором смысле. Содержание 1 Определения 2 Замечание 3 Примеры 4 Свойства … Википедия
Дискретное распределение — Функция вероятности в теории вероятностей наиболее часто используемый способ охарактеризовать дискретное распределение. Содержание 1 Определения 1.1 Функция произвольной вероятности … Википедия
Дискретное вейвлет-преобразование — Пример 1 го уровня дискретного вейвлет преобразования изображения. Вверху оригинальное полноцветное изображение, в середине вейвлет преобразование, сделанное по горизонтали исходного изображения (только канал яркости), внизу вейвлет… … Википедия
Дискретность пространства-времени
Данная концепция возникла еще во времена древней Греции. Зенон Элейский в своей апории «Ахиллес и черепаха», ставит под сомнение наше представление о бесконечной делимости пространства и времени.
«Допустим, Ахиллес бежит в десять раз быстрее, чем черепаха, и находится позади неё на расстоянии в тысячу шагов. За то время, за которое Ахиллес пробежит это расстояние, черепаха в ту же сторону проползёт сто шагов. Когда Ахиллес пробежит сто шагов, черепаха проползёт ещё десять шагов, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху.»
Концепция дискретного пространства-времени порождает ряд необычных следствий, что заставляет усомниться в ее справедливости. Но это только на первый взгляд.
Если бы удалось доказать, что элементарные частицы движутся только с одной, единственной скоростью, то это было бы сильным доводом в пользу принципа изотахии.
Разумеется, есть масса случаев, когда элементарные частицы двигались со скоростью, отличающейся от скорости света. Данную проблему можно преодолеть различными способами.
Первый вариант предполагает, что движение частиц носит прерывистый характер, то есть состояние движения сменяется состоянием покоя. Подобная идея встречается еще у арабских мыслителей в IX-XI веке.
«Если два тела кажутся нам движущимися с разными скоростями,то причиной этого различия не более быстрое и медленное движение, а то, что движение называемое нами медленным, прерывается промежутками покоя чаще, чем движения называемое быстрым»
Последним кто продвигал идею «прерывистого движения» был Г. Бек в 1929 г. Он предложил формулу для расчета скорости результирующего движения:
Также он предложил графическую интерпретацию прерывистого движения, по аналогу с азбукой Морзе, где движение обозначается как прямая, а состояния покоя как точка.
Второй вариант предполает, что частицы движутся не строго по прямой, а совершают колебания, вдоль основного направления. В первые это встречается у Эпикура в письме Геродоту,где он упоминает «дрожание атомов в глубине плотного тела».
Что значит при увеличении скорости движения тела (Vp), скорость «перемещения» ее во времени (Vt) уменьшается, данное предположение согласуется с теорий относительности, из которой следует, что увеличение скорости ведет к замедлению времени и наоборот.
Используемая литература: Вяльцев А.Н. » Дискретное пространство и время»
Споры о науке
143 поста 1.2K подписчика
Правила сообщества
Уважайте оппонентов и аргументируйте свои доводы. Ссылки на соответствующую литературу приветствуются.
>Если скорость будет больше V, то тело пройдет расстояние S за время меньшее чем T, что невозможно, поскольку T минимально возможное время
Неверно. Если скорость больше V, то это означает, что за минимально возможное время T тело пройдёт расстояние, скажем, 2S. Вы неправильно понимаете суть квантования времени. Уж не говоря о том, что это теория, не общепринятая, и значительно более сложная, чем Ахиллес, догоняющий черепаху.
И все же есть мнение, что пространство- время дискретны. Другое дело, что свойство изотахии, вытекающее из дискретности пространства времени, мы не наблюдаем. То есть различные тела могут иметь разную скорость. Однако скорость мы можем измерять только у «крупных» тел, наименьшее из которых (нам известных) это элементарные частицы. При этом квант времени и пространства, по-видимому, значительно меньше любой самой малой элементарной частицы и вероятно равен постоянной Планка.
А вот как так получается, что Ахиллес черепаху все же догнал?
Время в чёрной дыре
Что такое световые конусы? В чём разница между временем и пространством? Почему время и пространство меняются ролями внутри чёрной дыры? Что такое диаграмма Пенроуза? В видео от ScienceClic в моей озвучке.
Движение и покой
Новый способ визуализации общей теории относительности
Как правильно понять общую теорию относительности?
Что представляет из себя гравитация?
Что такое искривление пространства-времени?
И как его представить?
Ответы на эти и не только вопросы в данном видео. Приятного просмотра!
Спор Альберта и Нильса
После знаменитой Копенгагенской интерпретации квантовой механики в 1927 году, Альберт Эйнштейн встал в оппозиция складывающемуся новому взгляду на природу. Уже на самой конференции Эйнштейн вместе со своими товарищами в мысленном эксперименте (Эйнштейна-Подольского-Розена парадокс) попытались показать неполноту квантовой физики. Убежденность Эйнштейна носила и явный эмоциональный характер, говоря: “Думать так логически допустимо, но это настолько противоречит моему научному инстинкту, что я не могу отказаться от поисков более полной концепции”. В этом споре главным оппонентом Эйнштейна стал Нильс Бор, который вместе с Вернером Гейзенбергом и разработал Копенгагенскую интерпретацию, выразившуюся в двух принципах: принципе дополнительности Бора и принципе неопределенности Гейзенберга. В одном из писем Бору, Эйнштейн писал: “Я убеждён, что Бог не бросает кости”, на что Бор парировал: “Эйнштейн, не указывайте Богу, что делать”. В беседе с Абрахамом Пайсом, другим сторонником квантовой механики Эйнштейн позволил себе и такую реплику: “Вы и вправду думаете, что Луна существует лишь когда вы на неё смотрите?”.
Упорные арьергардные бои, которые Эйнштейн вел против наступающей со всех сторон квантовой механики, достигли наибольшего напряжения в Брюсселе, во время двух знаменитых Сольвеевских конгрессов. В обоих случаях Эйнштейн выступал как провокатор, пытаясь нащупать брешь в торжествующей победу новой премудрости.
На первом из них, состоявшемся в октябре 1927 года, присутствовали три великих мастера, стоявших у истоков новой эры в физике, но теперь скептически настроенных по отношению к ее детищу – таинственному миру квантовой механики. Там были семидесятичетырехлетний Хендрик Лоренц, шестидесятидевятилетний Макс Планк и сорокавосьмилетний Альберт Эйнштейн. Хендрику Лоренцу, получившему Нобелевскую премию за исследования электромагнитного излучения, оставалось жить всего несколько месяцев. Макс Планк был обладателем Нобелевской премии за теорию кванта, а Эйнштейн – за открытие закона фотоэлектрического эффекта.
Среди остальных двадцати шести участников конгресса больше половины тоже в свое время стали лауреатами Нобелевской премии. Здесь же были и все чудо-мальчики новой квантовой механики, надевшиеся либо переубедить, либо победить Эйнштейна. Это были двадцатипятилетний Вернер Гейзенберг, двадцатипятилетний Поль Дирак, двадцатисемилетний Вольфганг Паули, тридцатипятилетний Луи де Бройль и представитель Америки тридцатипятилетний Артур Комптон. Был и представитель среднего поколения сорокалетний Эрвин Шредингер, зажатый между “сердитыми молодыми людьми” и стариками-скептиками. И конечно, здесь был сорокадвухлетний Нильс Бор, в прошлом “сердитый молодой человек”, который своей моделью атома способствовавший появлению квантовой механики, а теперь стойкий защитник вступающих в противоречие с интуицией следствий из этой теории.
Сольвеевский конгресс 1927 года
Сольвеевский конгресс 1927 года
Лоренц попросил Эйнштейна сделать на конгрессе доклад о состоянии дел в квантовой механике. Эйнштейн сначала дал согласие, но потом отказался. “После длительных колебаний я пришел к выводу, что недостаточно подхожу для того, чтобы представить доклад, отражающий текущее положение дел, – ответил он. – Отчасти это связано с тем, что я не одобряю чисто статистический способ рассуждений, на котором основываются новые теории”. А затем он с горечью добавил: “Прошу вас, не сердитесь на меня”.
Вместо него доклад, открывший конгресс, сделал Бор. Он не скупился на похвалу, описывая достижения квантовой механики. В субатомном мире нет определенности и строго выполняющегося принципа причинности, говорил он. Нет детерминистских законов, только вероятности и шанс. Не имеет смысла говорить о “реальности”, не зависящей от процесса наблюдения и измерения. В зависимости от характера ставящегося эксперимента свет может быть либо волнами, либо частицами.
Во время официальных заседаний Эйнштейн говорил очень мало. “Я должен извиниться, что не разобрался в квантовой механике достаточно глубоко”, – заметил он в самом начале. Но за обедом и во время долгих вечерних разговоров, возобновлявшихся за завтраком, он втягивал Бора и его сторонников в оживленные споры, затравкой для которых служила его любимая шутка о Боге, который не играет в кости. “Нельзя строить теории на основании большого числа всяческих “если”, – вспоминает Паули доводы Эйнштейна. – Это глубоко неправильно, даже если основывается на опыте и логически непротиворечиво”.
“Вскоре дискуссия свелась к поединку между Эйнштейном и Бором, споривших о том, можно ли атомную теорию в ее нынешнем виде считать окончательной”, – вспоминал Гейзенберг. Как сказал впоследствии Эренфест своим студентам, “о, это было восхитительно”.
Смеющийся Нильс Бор и рассуждающий Альберт Эйнштейн
Смеющийся Нильс Бор и рассуждающий Альберт Эйнштейн
И во время заседаний, и в пылу неформальных дискуссий Эйнштейн пытался обработать своих противников, ставя искусные мысленные эксперименты, которые должны были доказать, что квантовая механика не дает полного описания реальности. С помощью хитроумного воображаемого устройства он пытался показать, что все характеристики движущейся частицы могут, по крайней мере в принципе, быть точно измерены.
Например, один из мысленных экспериментов Эйнштейна состоял в следующем. Пучок электронов пускают на экран со щелью. Пройдя через щель, электроны ударяются о фотографическую пластину, и их координаты фиксируются. Было еще много дополнительных элементов воображаемого прибора, таких, например, как задвижка, которая позволяла мгновенно открывать и закрывать щель. Все они были изобретательно использованы Эйнштейном, который хотел продемонстрировать, что теоретически можно одновременно знать точно координату и импульс электрона.
“Эйнштейн являлся на завтрак с каким-нибудь подобным предложением”, – вспоминал Гейзенберг. Происки Эйнштейна его, как и Паули, волновали не слишком. “Все будет в порядке, – твердили они, – все будет в порядке”. Но Бор часто приходил в возбуждение и начинал что-то исступленно бормотать.
Обычно в зал, где проходило заседание конгресса, они шли вместе, разрабатывая по пути стратегию, с помощью которой можно было бы показать несостоятельность идей Эйнштейна. “К обеду мы обычно уже могли доказать, что его мысленный эксперимент не противоречит принципу неопределенности, – вспоминал Гейзенберг, – и Эйнштейн признавал поражение. Но на следующее утро он появлялся за завтраком с новым, обычно более сложным мысленным экспериментом”. К обеду они уже знали, как опровергнуть и его.
Вернер Гейзенберг и Нильс Бор
Вернер Гейзенберг и Нильс Бор за «чашечкой» Карлсберг
Так это и продолжалось. Бору удалось отбить каждый мяч, посланный Эйнштейном, и показать, как принцип неопределенности в каждый момент времени действительно ограничивает доступную нам информацию о движущемся электроне. “Так продолжалось несколько дней, – рассказывает Гейзенберг. – И под конец мы – Бор, Паули и я – знали, что у нас под ногами твердая почва”.
“Эйнштейн, мне стыдно за вас”, – ворчал Эренфест. Он был огорчен из-за того, что в отношении квантовой механики Эйнштейн проявляет ту же неуступчивость, что когда-то физики-охранители в отношении теории относительности. “К Бору он сейчас относится точно так же, как воинствующие защитники одновременности относились к нему самому”.
Замечание, сделанное Эйнштейном в последний день конгресса, показывает, что принцип неопределенности был не единственным заботящим его аспектом квантовой механики. Его также волновало – и чем дальше, тем больше, – что квантовая механика, возможно, допускает действие на расстоянии. Другими словами, согласно копенгагенской интерпретации, нечто происшедшее с одним телом мгновенно определяет результат измерения свойств другого тела, расположенного в совершенно другом месте. Согласно теории относительности, пространственно разделенные частицы независимы. Если действие, произведенное над одним телом, немедленно влияет на другое тело, расположенное в отдалении от него, отметил Эйнштейн, “с моей точки зрения, это противоречит постулату теории относительности”. Никакая сила, включая гравитационную, не может передаваться со скоростью, превышающей скорость света, настаивал он.
Может, Эйнштейн и проиграл спор, но он, как и прежде, оставался звездой конгресса. Де Бройль, мечтавший о встрече с ним, увидел Эйнштейна первый раз и не был разочарован. “Меня особенно поразило спокойное, задумчивое выражение его лица, общая доброжелательность, простота и дружелюбие”, – вспоминал он.
Этим двоим поладить было легко, поскольку де Бройль, как и Эйнштейн, пытался понять, можно ли как-то спасти причинность и достоверность классической физики. В то время он работал над так называемой теорией двойного решения, которая, как он надеялся, позволит обосновать волновую механику с точки зрения классической физики.
“Школа индетерминистов, главные адепты которой были молоды и бескомпромиссны, встретила мою теорию с холодным неодобрением”, – вспоминал де Бройль. Эйнштейн же, наоборот, одобрительно отнесся к его усилиям. Возвращаясь в Берлин, до Парижа Эйнштейн ехал одним поездом с де Бройлем.
Прощальный разговор состоялся на платформе Северного вокзала. Эйнштейн сказал де Бройлю, что все научные теории, если оставить в стороне их математическое выражение, должны допускать такое простое изложение, “чтобы даже ребенок мог их понять”. А что может быть столь же непросто, продолжал Эйнштейн, как чисто статистическая интерпретация волновой механики! “Продолжайте, – напутствовал он де Бройля, расставаясь на станции. – Вы на правильном пути!”
Действительно, Эйнштейн оставался упрямой белой вороной. “Я восхищен достижениями нового поколения молодых физиков, известными как квантовая механика, и я верю, что во многом эта теория истинна, – сказал он в 1929 году, когда сам Планк вручал ему медаль своего имени. – Но (это “но” всегда присутствовало, когда Эйнштейн выступал в поддержку квантовой механики) я верю, что ограничения, накладываемые статистическими законами, будут сняты”.
Макс Планк вручает медаль своего имени Альберту Эйнштейну
Макс Планк вручает медаль своего имени Альберту Эйнштейну
Так была подготовлена сцена для еще более драматического, решающего сольвеевского поединка между Эйнштейном и Бором. Он состоялся на конгрессе, проходившем в октябре 1930 года. В теоретической физике столь увлекательные сражения случаются редко.
В этот раз, пытаясь поставить в тупик группу Бора – Гейзенберга и сохранить достоверность механики, Эйнштейн придумал еще более изощренный мысленный эксперимент. Как уже упоминалось, принцип неопределенности утверждает, что существует компромисс между возможностью точного измерения координаты частицы и точного измерения ее импульса. Кроме того, согласно тому же принципу неопределенность свойственна и процессу одновременного измерения энергии системы и времени, в течение которого происходит исследуемый процесс.
В мысленный эксперимент Эйнштейна входил ящик с излучением, снабженный затвором. Затвор открывается и закрывается так быстро, что за один цикл может вылететь только один фотон. Затвор контролируется точными часами. Ящик взвешивают и получают точное значение его веса. Затем в строго определенный момент времени затвор открывается, и вылетает один фотон. Ящик взвешивают снова. Связь между энергией и массой (помните, E = mc2) позволяет точно определить энергию. А зная показания часов, мы знаем точное время вылета фотона. Вот так-то!
Конечно, на самом деле есть ограничения, не позволяющие реально поставить такой эксперимент. Но теоретически он возможен и, следовательно, опровергает принцип неопределенности.
Ящик с затвором из мысленного эксперимента Альберта Эйнштейна
Брошенный вызов потряс Бора. “Он метался от одного к другому, пытаясь уговорить всех, что такого быть не может, что если Эйнштейн прав, значит, физике пришел конец, – записал один из участников конгресса. – Но опровержения он придумать не мог. Я никогда не забуду вид этих двух противников, выходящих из университетского клуба. Величественная фигура Эйнштейна, идущего спокойно, чуть улыбаясь иронически, и семенящего рядом с ним, ужасно огорченного Бора”.
Нильс Бор и Альберт Эйнштейн после знаменитого мыслительного эксперимента последнего
Нильс Бор и Альберт Эйнштейн после знаменитого мыслительного эксперимента последнего
По иронии судьбы в этом научном споре после бессонной ночи Бору удалось заманить Эйнштейна в расставленную им же самим ловушку. В этом мысленном эксперименте Эйнштейн не принял в расчет свое собственное величайшее открытие – теорию относительности. Согласно этой теории в сильном гравитационном поле часы идут медленнее, чем при более слабой гравитации. Эйнштейн об этом забыл, но Бор помнил. При испускании фотона масса ящика уменьшается. Ящик находится в гравитационном поле земли. Чтобы его можно было взвесить, ящик подвешен на пружинке со шкалой. После вылета фотона он несколько поднимается, и именно этот небольшой подъем обеспечивает неприкосновенность принципа неопределенности для энергии и времени.
“Главным здесь был учет связи между скоростью хода часов и их положением в гравитационном поле”, – вспоминал Бор. Отдавая должное Эйнштейну, он любезно помог ему выполнить вычисления, которые и принесли в этом раунде победу принципу неопределенности. Но окончательно переубедить Эйнштейна не удавалось никому и никогда. Даже год спустя он все еще продолжал перебирать различные варианты подобных мысленных экспериментов.
Кончилось все следующим: квантовая механика доказала, что как теория она вполне успешна, а Эйнштейн впоследствии пришел к тому, что можно назвать его собственным толкованием неопределенности. Он уже говорил о квантовой механике не как о неправильной теории, а только как о неполной. В 1931 году он номинировал Гейзенберга и Шредингера на Нобелевскую премию. (Гейзенберг был удостоен премии в 1932 году, а Шредингер – одновременно с Дираком – в 1933 году.) Предлагая их кандидатуры, Эйнштейн написал: “Я убежден, что эта теория, несомненно, содержит часть истины в последней инстанции”.
Эрвин Шредингер, король Швеции и Вернер Гейзинберг на вручении Нобелевской премии Шредингеру в 1933 году.
Эрвин Шредингер, король Швеции и Вернер Гейзинберг на вручении Нобелевской премии Шредингеру в 1933 году.
Часть истины в последней инстанции. Эйнштейн все еще полагал, что есть еще нечто за реальностью, определяемой копенгагенской интерпретацией квантовой механики.
Ее недостаток в том, что она “не претендует на описание физической реальности, а только на определение вероятности осуществления физической реальности, которую мы наблюдаем”. Так в том же году писал Эйнштейн в статье в честь Джеймса Клерка Максвелла, великого мастера столь любимого им теоретико-полевого подхода к физике. Он закончил ее, заявив во всеуслышание о своем кредо реалиста – откровенном отрицании утверждений Бора, что физика имеет отношение не к природе как таковой, а только к тому, “что мы можем сказать о природе”. Услышав такое Юм, Мах, да, возможно, и сам Эйнштейн, когда был моложе, подняли бы в удивлении брови. Но теперь он провозглашал: “Вера во внешний мир, не зависящий от воспринимающего его субъекта, является основой всех естественных наук”.
Карикатура на знаменитый афоризм Альберта Эйнштейна “Бог не играет в кости”: Бог, играющий в кости.
Карикатура на знаменитый афоризм Альберта Эйнштейна “Бог не играет в кости”: Бог, играющий в кости.
Когда осмыслил учебник физики за 7 класс
Дебаты о «Существовании Ничто» Нил Деграсс Тайсон, Лоуренс Краусс, Ричард Готт и другие
Перед вами четырнадцатая ежегодная Научная Конференция имени Айзека Азимова. В этот раз ее ведущий, Нил Деграсс Тайсон, с группой физиков, философов и журналистов ведет оживленную дискуссию о «Существовании Ничто». Концепция «Ничто» столь же стара, как «Ноль» сам по себе, и в этих дебатах участники охватят все, что человечеству о ней известно. Они проложат путь от древних греков, уравнения «Бог создал мир из Ничего», унаследованное от христианской метафизики до современных исследований в области квантовой гравитации.
Среди приглашенных специалистов вы сможете узнать Лоуренса Краусса — профессора физики, основателя проекта The Origins и любителя противоречивых тем. Остальные гости не столь известны русскоязычной аудитории, и перед вами отличный повод с ними познакомиться!
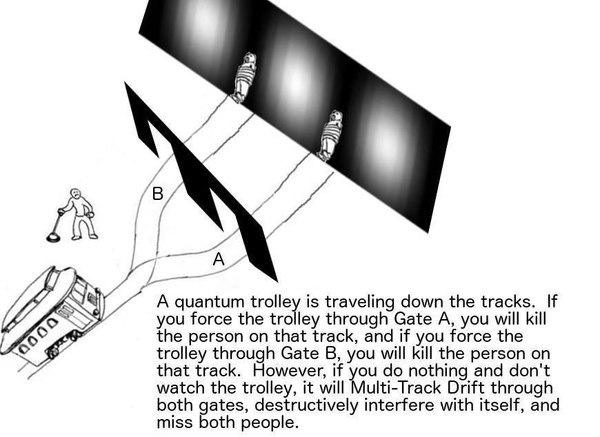
Квантовая вагонетка
Перевод: Квантовая вагонетка едет вниз по рельсам. Если вы направите вагонетку через ворота А, вы убьёте человека на этом пути, а если направите её через ворота Б — убьёте человека на том пути. Однако, если вы не будете делать ничего и не станете смотреть на вагонетку, она пройдёт по обоим путям, деструктивно проинтерферирует с собой и проедет мимо обоих людей.
О нашем мире, просто и интересно
В своих статьях попробую рассказать о строении всего, о теории обо всем и о том, как многие люди пришли к невероятным для своего времени рациональным открытиям, понятным языком.
Сам я любитель, очень увлекаюсь теориями о законах и строении мира. Ну а это вводная статья, если понравится, будет продолжение)
Итак, чтобы войти в курс дела, стоит начать с Ньютона и Эйнштейна, но мы не будем уделять им много времени.
В свое время Ньютон ввел понятие гравитации, но главное его достижение состоит в том, что он приравнял движущиеся без ускорения объекты к недвижимым.
Эту идею продолжил, на мой взгляд, самый выдающийся в области философии космологии Альберт Эйнштейн, сказав, что все в этом мире относительно. Если бы не было других планет, мы не могли бы понять, крутимся ли мы вокруг Солнца или оно вокруг нас. Только благодаря тому, что другие планеты крутятся вокруг Солнца, мы делаем этот вывод. Так же два человека в скафандрах, встретившиеся в космосе, не смогут сказать, кто движется относительно другого. Каждому из них будет казаться, что он стоит на месте, а другой летит мимо него.
Но такой концепции не соответствовали эксперименты с изучением света, и после лет исследований Эйнштейн принимает скорость света как абсолютную, максимальную скорость. Она составляет порядка 300000 км/с. С этого момента и начинается ломаться привычная картина мира. Как бы ты быстро ни двигался, свет всегда будет двигаться с такой скоростью. Это подтверждали и эксперименты, так что большинство физиков согласились с абсолютностью этой скоростью.
Но в такой модели возникает парадокс. Пусть в конце туннеля стоит стена на расстоянии 300000 км от лампы. Тогда для человека, стоящего у нее, свет долетит до стены за 1 секунду. Что же мы можем сказать про человека, летящего на ракете? Пусть его скорость составляет 150000 км/с. представим, что наблюдатель у лампы знает об абсолютности света и знает, что для человека на ракете скорость света равна 300000 км/с. Но тогда относительно человека у лампы скорость света человека на ракете будет составлять 450000 км/с. Если бы такая скорость была возможна, свет достиг бы стены в разное время, чего не может быть.
Эйнштейн решил этот парадокс, говоря, что при увеличении скорости в пространстве время меняет свой ход. Чем быстрее ты движешься, тем медленнее для тебя идет время (твои часы начнут отставать). Это свойство скорости и времени доказано множеством экспериментов на ракетах, самолетах, в астрономических обсерваториях. С ним связано множество парадоксов, но о них я говорить не буду, потому что тема статей немного не об этих парадоксах (если хотите, могу рассказать парочку в комментариях).
После этих исследований единственной большой работой Эйнштейна была работа над структурой пространство-время. Она не относится к теме, но я могу рассказать о ней также в следующем посте, если вам будет интересно.
А теперь перейдем к рассуждениям, для которых и потребуется мой предыдущий исторический экскурс.
Я же предлагаю качественно другой подход к понимаю сути измерений. Абсолютно другой.
Итак, начнем с 0. Что такое нульмерный мир? Точка. Просто точка, у которой нет размерностей.
Все привыкли (по крайней мере по-молодости) думать, что мы живем в трехмерном мире, именующимся пространством.
Но теперь представим себе четырехмерный мир. Что он должен из себя представлять? Бесконечное множество трехмерных миров, то есть бесконечное число пространств. А теперь подумайте о том, что каждый миг ВСЁ пространство вокруг нас изменяется. Каждый миг перед нами уже НОВОЕ пространство, так что с течение времени мы проходим бесконечно большое количество пространств. Не есть ли это четвертое измерение? Теперь вы смело можете говорить, что живете в четырехмерном мире.
Следующая моя статья будет посвящена построению идеального куба в четвертом (временном) измерении, расскажу как время переводить в пространство и наоборот, а затем расскажу, откуда берутся законы физики и о том, существую ли параллельные нам миры, ну и про пятое измерение, разумеется. Как обещалось, будет гораздо интереснее, это лишь вводная часть, спасибо, что дочитали)
Мне очень интересны обсуждения, вопросы и комментарии на эту тему, не стесняйтесь))