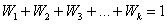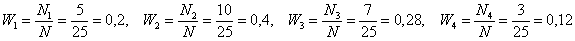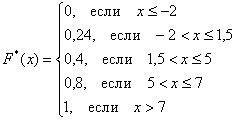Что такое дискретный ряд
2. Дискретный вариационный ряд.
Полигон частот и эмпирическая функция распределения
На вводном уроке по математической статистике мы узнали, что такое математическая статистика, и теперь обо всём подробнее. Далее для удобства я буду нумеровать статьи и постараюсь делать их не слишком длинными. Потому что всё действительно просто, и главное, здесь научиться рациональной технике вычислений, на которую и будет сделан особый упор.
Интервальные и дискретные вариационные ряды почти сразу же встретились в предыдущей статье, и мы начинаем с дискретного случая, когда количественная эмпирическая величина 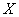
…что-то не понятно по терминам? Срочно изучать первый урок! (ссылка выше)
Дискретный вариационный ряд – это упорядоченное по возрастанию (как правило) множество вариант 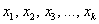
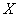
Частоты выборочной совокупности обозначают через 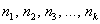
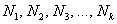
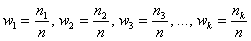
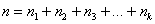
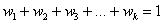
Аналогично для совокупности генеральной: 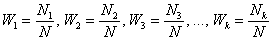
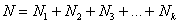
И тут вспоминается Пример 2 об оценках по матанализу в группе из 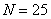
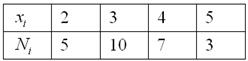
– пожалуйста, пример дискретного вариационного ряда, где варианты 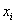
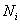
Для разминки найдём относительные частоты:
и непременно проконтролируем, что: 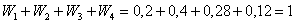
Все вычисления обычно проводят на калькуляторе либо в Экселе, а результаты заносят в таблицу, при этом, в статистике данные чаще располагают не в строках, а в столбцах: 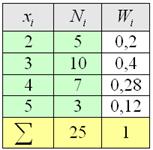
Такое расположение обусловлено тем, что количество вариант может быть достаточно велико, и они просто не вместятся в строчку. Не редкость, когда их 10-20, а бывает, и 100-200, что тоже и неоднократно встречалось в моей практике. И это не какие-то супер-пупер расчёты, а учебные задачи!
После сей позитивной новости продолжаем 🙂
Откуда берутся дискретные вариационные ряды? Такие ряды появляются в результате учёта дискретной характеристики статистической совокупности, причём, варианты ряда не отличаются большим разнообразием. Например, оценки (коих не так много) в примере выше.
И сейчас мы примем непосредственное участие в этом процессе:
По результатам выборочного исследования рабочих цеха были установлены их квалификационные разряды: 4, 5, 6, 4, 4, 2, 3, 5, 4, 4, 5, 2, 3, 3, 4, 5, 5, 2, 3, 6, 5, 4, 6, 4, 3. Требуется:
– составить вариационный ряд и построить полигон частот;
– найти относительные частоты и построить эмпирическую функцию распределения.
Чего томиться? – вся тема урока в одной задаче!
Решение: в условии прямо сказано о том, что перед нами выборка из генеральной совокупности (всех рабочих цеха), и первое, что логично сделать – подсчитать её объем, т.е. количество рабочих. В данном случае это легко сделать устно: 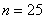
Квалификационные разряды – есть величина дискретная, и поэтому нам предстоит составить дискретный вариационный ряд (обратите внимание, что в условии ничего не сказано о характере ряда).
Если у вас под рукой нет вычислительных программ, то вручную (Эксель разберём ниже). При этом оптимальным может быть следующий алгоритм: сначала окидываем взглядом все числа и определяем среди них минимальное (примерно) и максимальное (примерно). В данном случае ориентировочный диапазон – от 1 до 7. Записываем их в столбец на черновике и обводим в кружочки. Далее начинаем вычёркивать карандашом числа из исходного списка: 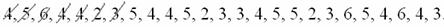
и делать около соответствующих кружков засечки:
После того, как все числа будут вычеркнуты, подсчитываем количество засечек в каждой строке: 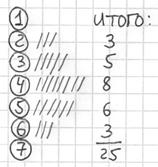
И обязательно проверяем, получается ли у нас в сумме объём выборки 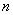
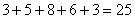

…ну что же, вполне и вполне логично – рабочих средней квалификации много, а учеников и мастеров – мало. Полученные результаты позволяют достаточно точно судить об уровне квалификации всего цеха (если, конечно, выборка представительна)
Построенный вариационный ряд также называют статистическим распределением выборки, причём, этот термин применИм не только для дискретного, но и для интервального ряда, который мы рассмотрим на следующем уроке.
Построим полигон частот. Это статистический аналог многоугольника распределения дискретной случайной величины (кто изучал). Полигон частот – это ломаная, соединяющая соседние точки 
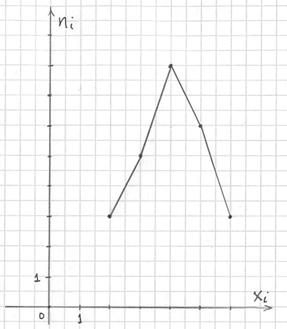
…эх, ностальгия. Но, пятилетку-другую, думается, так решать ещё будут.
Теперь современный способ:
Решаем! – исходные данные с пошаговой инструкцией прилагаются.
Вторая часть задачи. Найдём относительные частоты 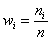
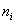

– обязательно проверяем, что сумма относительных частот равна единице!
Иногда требуется построить полигон относительных частот. Как вы правильно догадываетесь – это ломаная, соединяющая соседние точки 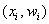
А теперь посмотрим на относительные частоты и задумаемся, на что они похожи? …Правильно, на вероятности. Так, например, можно сказать, что 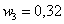
А вот если учесть ВСЕХ рабочих цеха (всю генеральную совокупность), то рассчитанные относительные частоты 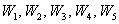
Построим эмпирическую функцию распределения 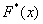
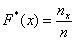
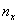
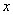
при этом «икс» «пробегает» все значения от «минус» до «плюс» бесконечности.
Очевидно, что на интервале 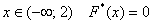
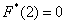
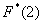
На промежутке 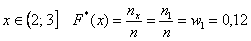
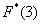
На промежутке 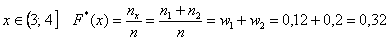
– если 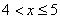

– если 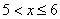
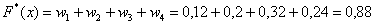
– и, наконец, если 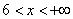
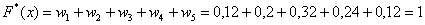
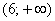
Накопленные относительные частоты удобно записывать в отдельный столбец таблицы, при этом алгоритм вычислений очень прост: сначала сносим слева 1-е значение (красная стрелка), а каждое следующее получаем как сумму предыдущего и относительной частоты из текущего левого столбца (зелёные обозначения): 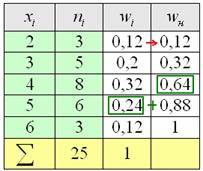
Вот, кстати, ещё один довод за вертикальную ориентацию данных – справа по надобности можно приписывать дополнительные столбцы.
Саму функцию принято записывать в кусочном виде:
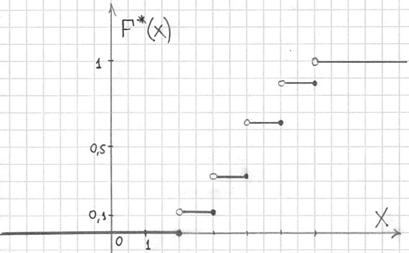
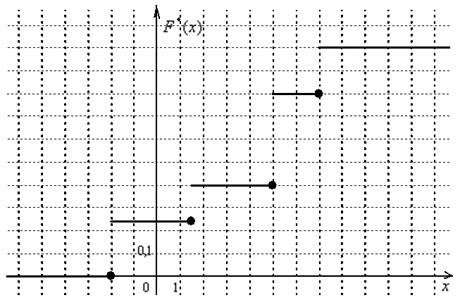
а её график представляет собой ступенчатую фигуру:
Эмпирическая функция распределения не убывает и принимает значения из промежутка 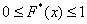
И сейчас мы автоматизируем процесс; видео, к сожалению, не вписалось по ширине, посему смотрим его на Ютубе:

Эмпирическая функция распределения 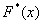
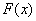
Миниатюрная задача для закрепления материала:
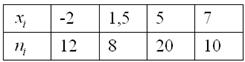
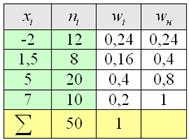
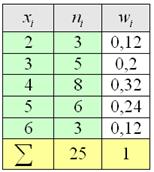
Дано статистическое распределение выборки
Составить эмпирическую функцию распределения, выполнить чертёж
Самостоятельно решить Пример 5 в Экселе, все числа и обозначения уже там.
Свериться с образцом можно ниже. По поводу красоты чертежа сильно не запаривайтесь, главное, чтобы было правильно – этого обычно достаточно для зачёта.
И я жду вас на третьем уроке, где речь пойдёт об интервальном вариационном ряде.
Пример 5. Решение: заполним расчётную таблицу:
Составим эмпирическую функцию распределения:
Выполним чертёж:
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5

Дискретный вариационный ряд и его характеристики
п.1. Классификация рядов распределения
Например:
Качественными признаками, которые не поддаются измерению, являются: профессия, пол, национальность и т.п.
Количественными признаками, которые можно подсчитать или измерить, являются: количество людей в группе, число повторений в опыте, возраст, вес, рост, скорость, температура и т.п.
Например:
Дискретными признаками, которые принимают отдельные значения, являются: количество людей в группе, число детей в семье, количество домов, число опытов и т.п.
Непрерывными признаками, которые могут принимать любые значения в интервале, являются: возраст, вес, рост, скорость, температура и т.п.
Распределение учеников по оценкам за контрольную работу
В данном ряду признак – это оценка, варианты признака \(x_i\) – это множество <2;3;4;5>, частоты \(f_i\) – это количество учеников, получивших каждую из оценок.
п.2. Дискретный вариационный ряд, полигон частот и кумулята
| Для распределения учеников по оценкам из нашего примера получаем такой полигон: |  |
Например:
Проведем необходимые расчеты и построим полигон относительных частот, кумуляту и эмпирическую функцию распределения учеников по оценкам.
| Оценка, \(x_i\) | 2 | 3 | 4 | 5 | Всего |
| К-во учеников, \(f_i\) | 3 | 15 | 10 | 5 | 33 |
| \(w_i\) | 0,0909 | 0,4545 | 0,3030 | 0,1515 | 1 |
| \(S_i\) | 0,0909 | 0,4545 | 0,8485 | 1 | — |
п.3. Выборочная средняя, мода и медиана
На полигоне частот мода – это абсцисса самой высокой точки.
Медиана дискретного вариационного ряда – это значение варианты посредине упорядоченного ряда.
На графике кумуляты медиана – это абсцисса первой точки слева, ордината которой превысила 0,5.
Например:
1) Найдем выборочную среднюю для распределения учеников по оценкам:
| Оценка, \(x_i\) | 2 | 3 | 4 | 5 | Всего |
| К-во учеников, \(f_i\) | 3 | 15 | 10 | 5 | 33 |
| \(x_if_i\) | 6 | 45 | 40 | 25 | 116 |
п.4. Степень асимметрии вариационного ряда
В рядах с асимметрией или выбросами выборочная средняя не отражает в полной мере особенности исследуемого признака. Типичный случай – значение среднего уровня доходов в странах с высоким индексом Джини, где 5% населения получает 95% доходов. Или анекдотичный случай со «средней температурой по больнице».
Поэтому, кроме средней, в статистическом исследовании всегда следует определять моду и медиану.
Например:
Для распределения учеников по оценкам мы получили \(X_
Т.к. средняя оказалась больше моды и медианы, наше распределение имеет правостороннюю асимметрию (что видно на полигоне частот – правый хвост длиннее).
При этом \(\frac<|M_o-X_
п.5. Выборочная дисперсия и СКО
Например:
1) Найдем выборочную дисперсию для распределения учеников по оценкам:
| Оценка, \(x_i\) | 2 | 3 | 4 | 5 | Всего |
| К-во учеников, \(f_i\) | 3 | 15 | 10 | 5 | 33 |
| \(x_i^2\) | 4 | 9 | 16 | 25 | — |
| \(x_i^2 f_i\) | 12 | 135 | 160 | 125 | 432 |
п.6. Исправленная выборочная дисперсия, стандартное отклонение выборки и коэффициент вариации
В теоретической статистике доказывается, что выборочная дисперсия D является смещенной оценкой дисперсии при распространении на генеральную совокупность.
А именно, выборочная дисперсия D всегда меньше математического ожидания для дисперсии генеральной совокупности.
Исправленная выборочная дисперсия S 2 является несмещенной оценкой.
Если показатель вариации V Внимание! Если исследуется не выборка, а вся генеральная совокупность, дисперсию «исправлять» не нужно.
п.7. Алгоритм исследования дискретного вариационного ряда
На входе: таблица с вариантами \(x_i\) и частотами \(f_i,\ i=\overline<1,k>\)
Шаг 1. Составить расчетную таблицу. Найти \(w_i,S_i,x_if_i,x_i^2,x_i^2f_i\)
Шаг 2. Построить полигон относительных частот (эмпирический закон распределения) и график кумуляты с эмпирической функцией распределения. Записать эмпирическую функцию распределения.
Шаг 3. Найти выборочную среднюю, моду и медиану. Проанализировать симметрию распределения.
Шаг 4. Найти выборочную дисперсию и СКО.
Шаг 5. Найти исправленную выборочную дисперсию, стандартное отклонение и коэффициент вариации. Сделать вывод об однородности выборки.
п.8. Примеры
Пример 1. На площадке фриланса была проведена выборка из 100 фрилансеров и подсчитано количество постоянных заказчиков, с которыми они работают.
В результате было получено следующее распределение:
| Число постоянных заказчиков | 0 | 1 | 2 | 3 | 4 | 5 |
| Число фрилансеров | 22 | 35 | 27 | 11 | 3 | 1 |
Исследуйте полученный вариационный ряд.
1) Вариационный ряд является дискретным.
Исследуемый признак – «число постоянных заказчиков».
Варианты признака \(x_i\in\left\<0;1;..;5\right\>\). Количество вариант k=6.
Составим расчетную таблицу:
| \(x_i\) | 0 | 1 | 2 | 3 | 4 | 5 | ∑ |
| \(f_i\) | 23 | 35 | 27 | 11 | 3 | 1 | 100 |
| \(w_i\) | 0,23 | 0,35 | 0,27 | 0,11 | 0,03 | 0,01 | — |
| \(S_i\) | 0,23 | 0,58 | 0,85 | 0,96 | 0,99 | 1 | — |
| \(x_if_i\) | 0 | 35 | 54 | 33 | 12 | 5 | 139 |
| \(x_i^2\) | 0 | 1 | 4 | 9 | 16 | 25 | — |
| \(x_i^2f_i\) | 0 | 35 | 108 | 99 | 48 | 25 | 315 |
\(X_
При этом \(\frac<|M_0-X_