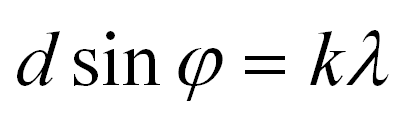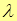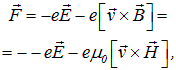Что такое дисперсия в оптике простыми словами
Дифракция и дисперсия света. Не путать!
Дисперсия света
Свет – электромагнитная волна. Видимый свет – это волны, имеющие длину в интервале от 380 до 770 нанометров.
Так вот, еще старина Ньютон заметил, что показатель преломления зависит от длины волны. Другими словами, красный свет, падая на поверхность и преломляясь, отклонится на другой угол, нежели желтый, зеленый и так далее. Эта зависимость и называется дисперсией.
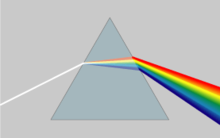
Пропуская белый свет через призму, можно получить спектр, состоящий из всех цветов радуги. Это явление напрямую объясняется дисперсией света. Раз показатель преломления зависит от длины волны, значит, он зависит и от частоты. Соответственно, скорость света для разных длин волн в веществе также будет различна
Дисперсия света – зависимость скорости света в веществе от частоты.
Где применяется дисперсия света? Да повсюду! Это не только красивое слово, но и красивое явление. Дисперсия света в быту, природе, технике и искусстве. Вот, например, дисперсия красуется на обложке альбома группы Pink Floyd.
Дифракция света
Интерференция света – это когда две когерентные световые волны при наложении усиливают друг друга или наоборот ослабляют.
Дифракцией света называется явление отклонения света от прямолинейного направления при прохождении вблизи преграды.
Дифракция проявляется не только для света, но и для других волн. Например, для звуковых. Или для волн на море. Отличный пример дифракции – это то, как мы слышим песню группы Пинк Флойд из проезжающей мимо машины, когда сами стоим за углом. Если бы звуковая волна распространялась прямо, она бы просто не достигла наших ушей, и мы бы стояли в полной тишине. Согласитесь, скучно. Зато с дифракцией гораздо веселее.
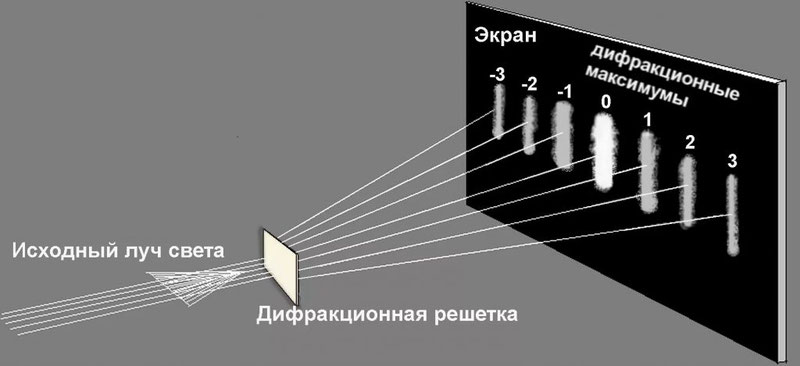
Для наблюдения явления дифракции используется специальный прибор – дифракционная решетка. Дифракционная решетка представляет собой систему препятствий, которые по размеру сопоставимы с длиной волны. Это специальные параллельные штрихи, выгравированные на поверхности металлической или стеклянной пластины. Расстояние между краями соседних щелей решетки называется периодом решетки или ее постоянной.
Что происходит со светом при прохождении дифракционной решетки? Попадая на решетку и встречая препятствие, световая волна проходит через систему прозрачных и непрозрачных областей, в результате чего разбивается на отдельные пучки когерентного света, которые после дифракции интерферируют друг с другом. Каждая длина волны отклоняется при этом на определенный угол, и происходит разложение света в спектр. В результате мы наблюдаем дифракцию света на решетке
Формула дифракционной решетки:
Здесь d – период решетки, фи – угол отклонения света после прохождения решетки, k – порядок дифракционного максимума, лямбда – длина волны.
Сегодня мы узнали, в чем чем заключается явления дифракции и дисперсии света. В курсе оптики очень сильно распространены задачи по теме интерференция, дисперсия и дифракция света. Авторы учебников очень любят подобные задачи. Чего нельзя сказать о тех, кому приходится их решать. Если Вы хотите легко справиться с заданиями, разобраться в теме, а заодно и сэкономить время, обратитесь к нашим авторам. Они помогут Вам справиться с любой задачей!
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
СОДЕРЖАНИЕ
Примеры
Материальная и волноводная дисперсия
Дисперсия материала в оптике
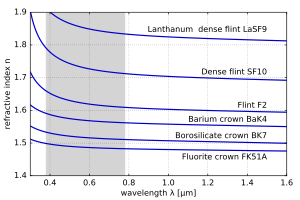
Для видимого света показатели преломления n большинства прозрачных материалов (например, воздуха, стекла) уменьшаются с увеличением длины волны λ :
На границе такого материала с воздухом или вакуумом (индекс
1) закон Снеллиуса предсказывает, что свет, падающий под углом θ к нормали, будет преломляться под углом arcsin ( грех θ / п ). Таким образом, синий свет с более высоким показателем преломления будет изгибаться сильнее, чем красный свет, что приведет к хорошо известному радужному узору.
Дисперсия групповой скорости
Параметр дисперсии групповой скорости :
часто используется для количественной оценки GVD, которая пропорциональна D через отрицательный фактор:
Контроль дисперсии
В волноводах
Волноводы обладают высокой дисперсией из-за своей геометрии (а не только из-за состава материала). Оптические волокна представляют собой своего рода волновод для оптических частот (света), широко используемых в современных телекоммуникационных системах. Скорость, с которой данные могут передаваться по одному волокну, ограничена расширением импульса из-за хроматической дисперсии среди других явлений.
В случае многомодовых оптических волокон так называемая модальная дисперсия также приведет к уширению импульса. Даже в одномодовых волокнах уширение импульса может происходить в результате дисперсии поляризационных мод (поскольку все еще существуют две поляризационные моды). Это не примеры хроматической дисперсии, поскольку они не зависят от длины волны или ширины полосы распространяемых импульсов.
Дисперсия высшего порядка в широкой полосе пропускания
Пространственная дисперсия
В электромагнетизме и оптике термин дисперсия обычно относится к вышеупомянутой временной или частотной дисперсии. Пространственная дисперсия относится к нелокальному отклику среды на пространство; это можно переформулировать как зависимость диэлектрической проницаемости от волнового вектора. Для примерной анизотропной среды пространственная связь между электрическим и электрическим полем смещения может быть выражена в виде свертки :
В геммологии
| Имя | B – G | C – F |
|---|---|---|
| Киноварь (HgS) | 0,40 | — |
| Synth. рутил | 0,330 | 0,190 |
| Рутил (TiO 2 ) | 0,280 | 0,120–0,180 |
| Анатаз (TiO 2 ) | 0,213–0,259 | — |
| Вульфенит | 0,203 | 0,133 |
| Ванадинит | 0,202 | — |
| Fabulite | 0,190 | 0,109 |
| Сфалерит (ZnS) | 0,156 | 0,088 |
| Сера (S) | 0,155 | — |
| Стибиотанталит | 0,146 | — |
| Гетит (FeO (OH)) | 0,14 | — |
| Брукит (TiO 2 ) | 0,131 | 0,12–1,80 |
| Цинкит (ZnO) | 0,127 | — |
| Линобат | 0,13 | 0,075 |
| Синтетический муассанит (SiC) | 0,104 | — |
| Касситерит (SnO 2 ) | 0,071 | 0,035 |
| Диоксид циркония (ZrO 2 ) | 0,060 | 0,035 |
| Пауэллит ( CaMoO 4 ) | 0,058 | — |
| Андрадит | 0,057 | — |
| Демантоид | 0,057 | 0,034 |
| Церуссит | 0,055 | 0,033–0,050 |
| Титанит | 0,051 | 0,019–0,038 |
| Бенитоит | 0,046 | 0,026 |
| Англезит | 0,044 | 0,025 |
| Бриллиант (С) | 0,044 | 0,025 |
| Бесцветное стекло | 0,041 | — |
| Гиацинт | 0,039 | — |
| Jargoon | 0,039 | — |
| Starlite | 0,039 | — |
| Циркон (ZrSiO 4 ) | 0,039 | 0,022 |
| GGG | 0,038 | 0,022 |
| Шеелит | 0,038 | 0,026 |
| Диоптаз | 0,036 | 0,021 |
| Whe Vinay wellite | 0,034 | — |
| Алебастр | 0,033 | — |
| Гипс | 0,033 | 0,008 |
| Эпидот | 0,03 | 0,012–0,027 |
| Ахроит | 0,017 | — |
| Кордиерит | 0,017 | 0,009 |
| Данбурит | 0,017 | 0,009 |
| Дравит | 0,017 | — |
| Эльбаите | 0,017 | — |
| Гердерит | 0,017 | 0,008–0,009 |
| Hiddenite | 0,017 | 0,010 |
| Индиколит | 0,017 | — |
| Лиддикоатит | 0,017 | — |
| Кунсайт | 0,017 | 0,010 |
| Рубеллит | 0,017 | 0,008–0,009 |
| Шерл | 0,017 | — |
| Скаполит | 0,017 | — |
| Сподумен | 0,017 | 0,010 |
| Турмалин | 0,017 | 0,009–0,011 |
| Верделит | 0,017 | — |
| Андалузит | 0,016 | 0,009 |
| Барит ( BaSO 4 ) | 0,016 | 0,009 |
| Евклаз | 0,016 | 0,009 |
| Александрит | 0,015 | 0,011 |
| Хризоберилл | 0,015 | 0,011 |
| Гамбергит | 0,015 | 0,009–0,010 |
| Фенакит | 0,01 | 0,009 |
| Родохрозит | 0,015 | 0,010–0,020 |
| Силлиманит | 0,015 | 0,009–0,012 |
| Смитсонит | 0,014–0,031 | 0,008–0,017 |
| Амблигонит | 0,014–0,015 | 0,008 |
| Аквамарин | 0,014 | 0,009–0,013 |
| Берил | 0,014 | 0,009–0,013 |
| Бразильянит | 0,014 | 0,008 |
| Селестина | 0,014 | 0,008 |
| Гошенит | 0,014 | — |
| Гелиодор | 0,014 | 0,009–0,013 |
| Морганит | 0,014 | 0,009–0,013 |
| Пироксмангит | 0,015 | — |
| Synth. шеелит | 0,015 | — |
| Доломит | 0,013 | — |
| Магнезит (MgCO 3 ) | 0,012 | — |
| Synth. изумруд | 0,012 | — |
| Synth. александрит | 0,011 | — |
| Synth. сапфир (Al 2 O 3 ) | 0,011 | — |
| Фосфофиллит | 0,010–0,011 | — |
| Энстатит | 0,010 | — |
| Анортит | 0,009–0,010 | — |
| Актинолит | 0,009 | — |
| Еремеевит | 0,009 | — |
| Нефелин | 0,008–0,009 | — |
| Апофиллит | 0,008 | — |
| Hauyne | 0,008 | — |
| Натролит | 0,008 | — |
| Synth. кварц (SiO 2 ) | 0,008 | — |
| Арагонит | 0,007–0,012 | — |
| Авгелит | 0,007 | — |
| Танзанит | 0,030 | 0,011 |
| Тулит | 0,03 | 0,011 |
| Цоизит | 0,03 | — |
| YAG | 0,028 | 0,015 |
| Альмандин | 0,027 | 0,013–0,016 |
| Гессонит | 0,027 | 0,013–0,015 |
| Спессартин | 0,027 | 0,015 |
| Уваровит | 0,027 | 0,014–0,021 |
| Виллемит | 0,027 | — |
| Pleonaste | 0,026 | — |
| Родолит | 0,026 | — |
| Борацит | 0,024 | 0,012 |
| Криолит | 0,024 | — |
| Ставролит | 0,023 | 0,012–0,013 |
| Пироп | 0,022 | 0,013–0,016 |
| Диаспора | 0,02 | — |
| Гроссуляр | 0,020 | 0,012 |
| Гемиморфит | 0,020 | 0,013 |
| Кианит | 0,020 | 0,011 |
| Перидот | 0,020 | 0,012–0,013 |
| Шпинель | 0,020 | 0,011 |
| Везувианит | 0,019–0,025 | 0,014 |
| Клиноцоизит | 0,019 | 0,011–0,014 |
| Лабрадорит | 0,019 | 0,010 |
| Аксинит | 0,018–0,020 | 0,011 |
| Эканите | 0,018 | 0,012 |
| Корнерупин | 0,018 | 0,010 |
| Корунд (Al 2 O 3 ) | 0,018 | 0,011 |
| Родизит | 0,018 | — |
| Рубин (Al 2 O 3 ) | 0,018 | 0,011 |
| Сапфир (Al 2 O 3 ) | 0,018 | 0,011 |
| Сингалит | 0,018 | 0,010 |
| Содалит | 0,018 | 0,009 |
| Synth. корунд | 0,018 | 0,011 |
| Диопсид | 0,018–0,020 | 0,01 |
| Изумруд | 0,014 | 0,009–0,013 |
| Топаз | 0,014 | 0,008 |
| Аметист (SiO 2 ) | 0,013 | 0,008 |
| Ангидрит | 0,013 | — |
| Апатит | 0,013 | 0,010 |
| Апатит | 0,013 | 0,008 |
| Авантюрин | 0,013 | 0,008 |
| Цитрин | 0,013 | 0,008 |
| Морион | 0,013 | — |
| Празиолит | 0,013 | 0,008 |
| Кварц (SiO 2 ) | 0,013 | 0,008 |
| Дымчатый кварц (SiO 2 ) | 0,013 | 0,008 |
| Розовый кварц (SiO 2 ) | 0,013 | 0,008 |
| Альбит | 0,012 | — |
| Bytownite | 0,012 | — |
| Полевой шпат | 0,012 | 0,008 |
| Лунный камень | 0,012 | 0,008 |
| Ортоклаз | 0,012 | 0,008 |
| Поллюцит | 0,012 | 0,007 |
| Санидин | 0,012 | — |
| Солнечный камень | 0,012 | — |
| Бериллонит | 0,010 | 0,007 |
| Канкринит | 0,010 | 0,008–0,009 |
| Лейцит | 0,010 | 0,008 |
| Обсидиан | 0,010 | — |
| Стронцианит | 0,008–0,028 | — |
| Кальцит (CaCO 3 ) | 0,008–0,017 | 0,013–0,014 |
| Флюорит (CaF 2 ) | 0,007 | 0,004 |
| Гематит | 0,500 | — |
| Синтетический касситерит (SnO 2 ) | 0,041 | — |
| Ганите | 0,019–0,021 | — |
| Датолит | 0,016 | — |
| Тремолит | 0,006–0,007 | — |
В изображении
Выбросы пульсаров
т знак равно k D M ⋅ ( D M ν 2 ) <\ Displaystyle т = К _ <\ mathrm
где дисперсионная постоянная k DM определяется выражением
с единицей парсеков на кубический сантиметр (1 пк / см 3 = 30,857 × 10 21 м −2 ).
Обычно для астрономических наблюдений эта задержка не может быть измерена напрямую, поскольку время излучения неизвестно. Что можно измерить, так это разницу во времени прихода на двух разных частотах. Задержка Δ t между высокочастотной ν hi и низкочастотной ν lo составляющей импульса будет
Перепись приведенного выше уравнения в терминах Δ t позволяет определить DM путем измерения времени прихода импульсов на нескольких частотах. Это, в свою очередь, может быть использовано для изучения межзвездной среды, а также позволяет комбинировать наблюдения пульсаров на разных частотах.
6.2. Дисперсия света
Дисперсия света — это зависимость показателя преломления n вещества от длины волны света (в вакууме)
или, что то же самое, зависимость фазовой скорости световых волн от частоты:
Дисперсией вещества называется производная от n по
Дисперсия — зависимость показателя преломления вещества от частоты волны – особенно ярко и красиво проявляет себя совместно с эффектом двойного лучепреломления (см. Видео 6.6 в предыдущем параграфе), наблюдаемом при прохождении света через анизотропные вещества. Дело в том, что показатели преломления обыкновенной и необыкновенной волн различно зависят от частоты волны. В результате цвет (частота) света прошедшего через анизотропное вещество помещенное между двумя поляризаторами зависит как от толщины слоя этого вещества, так и от угла между плоскостями пропускания поляризаторов.
Для всех прозрачных бесцветных веществ в видимой части спектра с уменьшением длины волны показатель преломления увеличивается, то есть дисперсия вещества отрицательна: 
Нормальная дисперсия вещества — это отрицательная дисперсия
Если вещество поглощает свет в каком-то диапазоне длин волн (частот), то в области поглощения дисперсия
оказывается положительной и называется аномальной (рис. 6.7, область 2–3).
Рис. 6.7. Зависимость квадрата показателя преломления (сплошная кривая) и коэффициента поглощения света веществом
(штриховая кривая) от длины волны l вблизи одной из полос поглощения (
Изучением нормальной дисперсии занимался ещё Ньютон. Разложение белого света в спектр при прохождении сквозь призму является следствием дисперсии света. При прохождении пучка белого света через стеклянную призму на экране возникает разноцветный спектр (рис. 6.8).
Рис. 6.8. Прохождение белого света через призму: вследствие различия значений показателя преломления стекла для разных
длин волн пучок разлагается на монохроматические составляющие — на экране возникает спектр
Наибольшую длину волны и наименьший показатель преломления имеет красный свет, поэтому красные лучи отклоняются призмой меньше других. Рядом с ними будут лучи оранжевого, потом желтого, зеленого, голубого, синего и, наконец, фиолетового света. Произошло разложение падающего на призму сложного белого света на монохроматические составляющие (спектр).
Ярким примером дисперсии является радуга. Радуга наблюдается, если солнце находится за спиной наблюдателя. Красные и фиолетовые лучи преломляются сферическими капельками воды и отражаются от их внутренней поверхности. Красные лучи преломляются меньше и попадают в глаз наблюдателя от капелек, находящихся на большей высоте. Поэтому верхняя полоса радуги всегда оказывается красной (рис. 26.8).
Рис. 6.9. Возникновение радуги
Используя законы отражения и преломления света, можно рассчитать ход световых лучей при полном отражении и дисперсии в дождевых каплях. Оказывается, что лучи рассеиваются с наибольшей интенсивностью в направлении, образующем угол около 42° с направлением солнечных лучей (рис. 6.10).
Рис. 6.10. Расположение радуги
Геометрическое место таких точек представляет собой окружность с центром в точке 0. Часть ее скрыта от наблюдателя Р под горизонтом, дуга над горизонтом и есть видимая радуга. Возможно также двойное отражение лучей в дождевых каплях, приводящее к радуге второго порядка, яркость которой, естественно, меньше яркости основной радуги. Для нее теория дает угол 51°, то есть радуга второго порядка лежит вне основной. В ней порядок цветов заменен на обратный: внешняя дуга окрашена в фиолетовый цвет, а нижняя — в красный. Радуги третьего и высших порядков наблюдаются редко.
Элементарная теория дисперсии. Зависимость показателя преломления вещества от длины электромагнитной волны (частоты) объясняется на основе теории вынужденных колебаний. Строго говоря, движение электронов в атоме (молекуле) подчиняется законам квантовой механики. Однако для качественного понимания оптических явлений можно ограничиться представлением об электронах, связанных в атоме (молекуле) упругой силой. При отклонении от равновесного положения такие электроны начинают колебаться, постепенно теряя энергию на излучение электромагнитных волн или передавая свою энергию узлам решетки и нагревая вещество. В результате этого колебания будут затухающими.
При прохождении через вещество электромагнитная волна воздействует на каждый электрон с силой Лоренца:
где v — скорость колеблющегося электрона. В электромагнитной волне отношение напряженностей магнитного и электрического полей равно
Поэтому нетрудно оценить отношение электрической и магнитной сил, действующих на электрон:
Электроны в веществе движутся со скоростями, много меньшими скорости света в вакууме:
Таким образом, можно считать, что при прохождении через вещество электромагнитной волны на каждый электрон действует только электрическая сила:
где 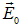

где, 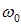
Следовательно, смещение электрона из положения равновесия пропорционально напряженности электрического поля. Смещениями ядер из положения равновесия можно пренебречь, так как массы ядер весьма велики по сравнению с массой электрона.
Атом со смещенным электроном приобретает дипольный момент
(для простоты положим пока, что в атоме имеется только один «оптический» электрон, смещение которого вносит определяющий вклад в поляризацию). Если в единице объема содержится N атомов, то поляризованность среды (дипольный момент единицы объема) можно записать в виде
В реальных средах возможны разные типы колебаний зарядов (групп электронов или ионов), вносящих вклад в поляризацию. Эти типы колебаний могут иметь разные величины заряда еi и массы тi, а также различные собственные частоты 
Безразмерный коэффициент пропорциональности fk характеризует эффективный вклад каждого типа колебаний в общую величину поляризации среды: