Что такое длина ломаной 8 класс геометрия

Ломаная линия

Ломаная линия — это геометрическая фигура, состоящая из последовательно соединённых отрезков, в которой конец одного отрезка является началом следующего. При этом соседние (имеющие общую точку) отрезки не должны лежать на одной прямой.

Отрезки, из которых состоит ломаная, называются её звеньями, а концы этих отрезков — вершинами ломаной.

Построим ломаную из четырёх отрезков:

Замкнутая и незамкнутая ломаная

Незамкнутая ломаная — это ломаная линия, концы которой не совпадают друг с другом:

незамкнутая ломаная ABCD.

Замкнутая ломаная — это ломаная линия, концы которой совпадают друг с другом:

замкнутая ломаная ABC.

Самопересекающаяся ломаная

Замкнутые и незамкнутые ломаные линии могут быть самопересекающимися. Самопересекающаяся ломаная — это ломаная линия, звенья которой пересекают другу друга в одной или нескольких точках. Например:

точки F, T, K — точки самопересечения, то есть точки, в которых ломаная пересекает сама себя.

Длина ломаной

Длина ломаной — это сумма длин всех её звеньев. Длина замкнутой ломаной, не имеющий самопересечений, то есть длина многоугольника, называется периметром.

Пример 1. Найти длину ломаной из 3 звеньев.

Решение: Для нахождения длины ломаной, состоящей из трёх звеньев, надо сложить длины всех её звеньев. Длина ломаной ABCD будет равна:

AB + BC + CD = 4 см + 3 см + 2 см = 9 см.

Ответ: Длина ломаной ABCD равна 9 см.

Пример 2. Найти длину замкнутой ломаной.

Решение: Найдём периметр замкнутой ломаной, сложив длины всех её звеньев:

AB + BC + CD + DA =
3 см + 5 см + 4 см + 5 см = 17 см.

Источник

Определение и характеристики ломаной геометрической фигуры

Ломаной называется особая разновидность геометрической фигуры, которая составлена из нескольких отрезков. Эти отрезки последовательно соединены между собой своими концами. Конец каждого отрезка, за исключением последнего, является начальной точкой следующего. Смежные отрезки не должны находиться на одной прямой линии.

Существует и другое определение того, что такое ломаная фигура. Согласно ему это геометрический объект, который представляет собой непрямую линию и состоит из череды отрезков, последовательно соединенных между собой. Эти отрезки могут образовывать углы различной величины. Даже если угол между ними будет минимальным, он все равно будет ломать линию и ее уже можно считать ломаной. В этом и заключается ее основное отличие от прямой.

Ломаную линию следует отличать от кривой. Основное отличие заключается в том, что отрезки ломаной являются прямыми линиями, а отрезки кривой — нет. Эти понятия подробно объяснит школьная программа по математике за 8 класс.

Звенья, вершины и длина

Чтобы полностью усвоить сущность и свойства этого понятия, рассмотрим, что такое звенья ломаной линии в математике, а также что представляют собой ее вершины и длина:

Интересно знать: что такое выпуклый четырехугольник, его особенности и признаки.

Обозначение ее составляется из заглавных латинских букв, которые стоят на вершинах:

В целом такую совокупность принято называть ABCDE или EDCBA.

Обратите внимание: что такое луч в геометрии.

Разновидности

В геометрии принято различать несколько разновидностей по структуре:

Как уже было описано выше, замкнутая непересекающаяся фигура получила название многоугольника.

Если звенья фигуры имеют пересечения между собой — она называется самопересекающейся.

Многоугольники

Многоугольник — это геометрическая фигура, которая характеризуется количеством углов и звеньев. Углы составлены парами звеньев замкнутой ломаной, сходящимися в одной точке. Звенья называются еще сторонами многоугольника. Общие точки двух отрезков называют вершинами многоугольника.

Количество звеньев или сторон в каждом многоугольнике соответствует количеству углов в нем же. Замкнутая ломаная из трех отрезков называется треугольником. Ломаная из четырех звеньев получила название четырехугольника. Фигура из пяти отрезков — пятиугольник и т. д.

Часть плоскости, которая ограничена замкнутой ломаной, называется плоским многоугольником. Другое ее название — многоугольная область.

Свойства

Ниже приведены основные свойства, общие для всех многоугольников:

Треугольники

Треугольником в математике принято называть плоскую геометрическую фигуру, которая состоит из трех точек, не располагающихся на одной прямой. Эти точки соединены тремя отрезками.

Точки представляют собой вершины или треугольника, а отрезки — его стороны. Возле каждой из вершин образуется угол треугольника. Таким образом эта фигура имеет три угла, что видно из ее названия.

Различают следующие виды треугольников:

Четырехугольники

Плоская геометрическая фигура, имеющая четыре угла и четыре стороны, называется четырехугольником.

Если все углы у четырехугольника прямые — это прямоугольник.

Правильный четырехугольник носит название квадрата.

Существуют и другие разновидности четырехугольников — ромб, трапеция, параллелограмм и пр. Все они подчиняются общим правилам, описанным выше.

Источник

Что такое длина ломаной 8 класс геометрия

ОПРЕДЕЛЕНИЯ

Ломаная А₁А₂А₃…А_n — фигура, состоящая из точек А₁, А₂, А₃, …, А_n и отрезков А₁А₂, А₂А₃, …, А_n-1А_n, которые их соединяют. Точки А₁, А₂, А₃, …, А_n называют вершинами ломаной, а отрезки А₁А₂, А₂А₃, …, А_n-1А_n — звеньями ломаной.

Простая лoманая — лoманая, не имеющая точек самопересечения.
Замкнутая лoманая — лoманая, концы которой соединяются.
Длина ломаной — сумма длин ее звеньев.

Многоугольник — простая замкнутая ломаная, соседние звенья которой не лежат на одной прямой; вершины ломаной называют вершинами многоугольника, а звенья ломаной — сторонами многоугольника. Многоугольник с n вершинами (n сторонами) называют n-угольником.

Диагональ многоугольника — отрезки, соединяющие несоседние вершины многоугольника.
Выпуклый многoугольник — многоугoльник, лежащий в одной полуплоскости относительно любой прямой, содержащей его сторону.
Угол выпуклого многоугольника при данной вершине — угол, образованный его сторонами, сходящимися в этой вершине.
Внешний угол выпуклого многоугольника при данной вершине — угол, смежный с внутренним углом многоугольника при этой вершине.

ПРИМЕРЫ РЕШЕНИЯ КЛЮЧЕВЫХ ЗАДАЧ

Задача № 1. Дано: ABCD — четырехугольник; ∠A = ∠B = ∠C; ∠D = 135.
Найти: ∠A, ∠B, ∠C.

Задача № 2. Дано: ABCDE — четырехугольник; ∠A : ∠B : ∠C : ∠D : ∠E = 1 : 2 : 3 : 4 : 8. Найти: ∠A, ∠B, ∠C, ∠D, ∠E.

Это конспект по теме «Ломаная. Многоугольник + ЗАДАЧИ». Выберите дальнейшие действия:

Источник

Ломаная

Определение 1. Ломаной (ломаной линией) \( \small A_1A_2. A_A_n \) называется геометрическая фигура, которая состоит из \( \small [ A_1A_2 ],\) \( \small [ A_2A_3 ]. \) \( \small [ A_A_n ]\) последовательно соединенных своими концами отрезков и никакие последовательные две отрезки\( \small [ A_A_ ]\) и \( \small [ A_A_ ]\) при \( \small k=1,2. n-2 \) не лежат на одной прямой.

Можно дать и другое определение ломаной:

Невырожденная ломаная

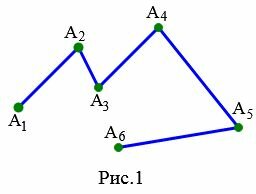
Ломаная, описанная в определении 1 называется невырожденной ломаной.

На рисунке 1 ломаная \( \small A_1A_2A_3A_4A_5A_6 \) является невырожденной поскольку отрезки \( \small [ A_1A_2 ]\) и \( \small [ A_2A_3 ]\), \( \small [ A_2A_3 ]\) и \( \small [ A_3A_4 ]\), \( \small [ A_3A_4 ]\) и \( \small [ A_4A_5 ]\), \( \small [ A_4A_5 ]\) и \( \small [ A_5A_6 ]\) не лежат на одной прямой.

Вырожденная ломаная

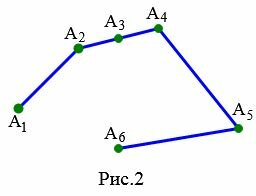На рисунке 2 изображена ломаная \( \small A_1A_2A_3A_4A_5A_6 \). Эта ломаная является вырожденной поскольку отрезки \( \small [ A_2A_3 ]\) и \( \small [ A_3A_4 ]\) лежат на одной прямой.

Внимание! Если явно не указыается вырожденность ломаной, то подразумевается невырожденная ломаная.

Звенья ломаной

Звеньями называют отрезки, из которых состоит ломаная.

Вершины ломаной

Конечные точки звеньев ломаной называются вершинами.

На рисунке 1 изображена ломаная \( \small A_1A_2A_3A_4A_5A_6 \), состоящая из шести вершин: \( \small A_1, \ A_2, \ A_3, \ A_4, \ A_5, \ A_6 \).

Смежные звенья ломаной

Смежные звенья ломаной − это звенья имеющие общую вершину.

На рисунке 3 смежными звеньями ломаной \( \small A_1A_2A_3A_4A_5A_6 \) являются звенья: \( \small [ A_1A_2 ]\) и \( \small [ A_2A_3 ]\), \( \small [ A_2A_3 ]\) и \( \small [ A_3A_4 ]\), \( \small [ A_3A_4 ]\) и \( \small [ A_4A_5 ]\), \( \small [ A_4A_5 ]\) и \( \small [ A_5A_6 ]\).

Смежные вершины ломаной

Смежными вершинами ломаной называют вершины одного звена ломаной.

На рисунке 3 смежными вершинами ломаной \( \small A_1A_2A_3A_4A_5A_6 \) являются вершины: \( \small A_1\) и \( \small A_2\), \( \small A_2\) и \( \small A_3\), \( \small A_3\) и \( \small A_4 \), \( \small A_4\) и \( \small A_5\), \( \small A_5\) и \( \small A_6\).

Незамкнутая ломанная

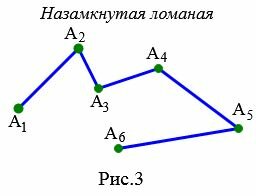
Незамкнутым является ломаная, первая и последняя точки которой не совпадают друг с другом (Рис.3).

Замкнутая ломанная

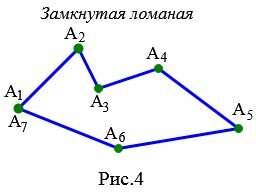На рисунке 4 ломаная \( \small A_1A_2A_3A_4A_5A_6A_7 \) является замкнутым, так как точки: \( \small A_1\) и \( \small A_7\) совпадают и отрезки \( \small A_1A_2\) и \( \small A_6A_7\) не лежат на одной прямой.

Ломаная с самопересечением

Ломаная имеет самопересечение, если хотя бы два ее звена имеют общую точку, помимо общей вершины.

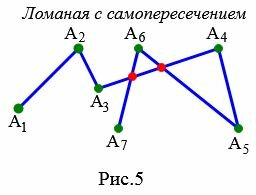Ни рисунке 5 ломаная \( \small A_1A_2A_3A_4A_5A_6A_7 \) имеет самопересечение, так как звенья \( \small A_5A_6 \) и \( \small A_6A_7 \) имеют общие точки со звеном \( \small A_3A_4 \).

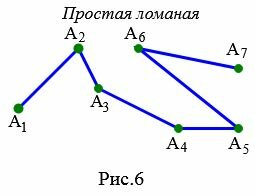
Простая ломаная

Ломаная называется простым, если не имеет самопересечений. Пример простой ломаной изображен на рисунке 6.

Длина ломаной

Длина ломаной равна сумме длин всех звеньев ломаной: \( \small d= A_1A_2+A_2A_3+. +A_A_n, \) где \( \small n \) − количество вершин ломаной.

Теорема. Длина ломаной больше расстояния между первым и последним точками.

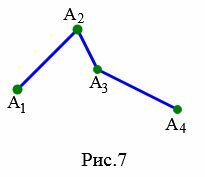Доказательство. Для доказательства теоремы рассмотрим ломаную \( \small A_1A_2A_3A_4 \) с тремя звеньями (Рис.7). Так как ломаная невырождена, то вершины \( \small A_1, \ A_2, \ A_3 \) не лежат на одной прямой. Тогда имеет место неравенство треугольников:

Для точек \( \small A_1, \ A_3, \ A_4 \) имеет место следующее нестрогое неравенство:

В выражении (2) мы не применяли строгое неравенство поскольку вершины \( \small A_1, \ A_3, \ A_4 \) ломаной не являются соседними вершинами и могут лежать на одной прямой.

В неравенстве (2) вместо слагаемого \( \small A_1 A_3\) подставим сумму \( \small A_1A_2+A_2A_3 \) из (1), которая больше, чем \( \small A_1 A_3\). Тогда получим:

Поседнее неравенство означает, что длина невырожденной ломаной больше расстояния между первым и последним точками.

Аналогично доказывается теорема для ломанной с любым количеством звеньев.

Источник

Ломаная линия

Ломаная линия — это геометрическая фигура, состоящая из отрезков, последовательно соединённых своими концами. Ломаной (ломаной линией). называется фигура, которая состоит из отрезков. Точки называются вершинами ломаной, а отрезки звеньями ломаной.

Содержание:

Понятие ломаной

На рисунке 2.39 изображены несколько точек которые последовательно соединены отрезками В результате получилась геометрическая фигура , которая называется ломаной.

Определение. Ломаной называется фигура, которая состоит из точек и соединяющих их отрезков Точки называются вершинами ломаной, а отрезки — звеньями ломаной.

При построении ломаной соседние отрезки не должны лежать на одной прямой. Точки называются соответственно началом и концом ломаной, а составляющие ее отрезки называются звеньями ломаной (рис. 2.39).

Определение. Если концы ломаной совпадают, то ее называют замкнутой.

На рисунках 2.41, 2.42, 2.44 изображены замкнутые ломаные.

Ломаная иногда может пересекать сама себя, т. е. не соседние по порядку звенья ломаной имеют общие точки. В этом случае ломаная называется самопересекающейся или непростой (рис. 2.43, 2.44). Если таких самопересечений нет, то ломаная называется простой. На рис. 2.40, 2.41 изображены простые ломаные.

Длина ломаной

Длина ломаной равна сумме длин ее звеньев.

Можно доказать теорему о длине ломаной.

Теорема 3.

Длина ломаной больше расстояния между ее концами.

Пример:

Звенья ломаной EFMO таковы: EF = 1 см, FM = 4 см, МО = 2 см. Может ли отрезок ЕО равняться: а) 0,5 см; б) 8 см?

Решение:

Из условия задачи имеем:

2. EF = 1 см, FM = 4 см, МО = 2 см. (рис. 2.45)

3. Может ли отрезок ЕО равняться: а) 0,5 см; б) 8 см.

На рис. 2.45 нет отрезка ЕО.

4. Построим отрезок ЕО (построение) (рис. 2.46).

Связь между данной ломаной EFMO и отрезком ЕО определяет теорема о длине ломаной.

5. Длина ломаной EFMO должна быть не меньше длины отрезка ЕО (1, 2, 4, теорема 3).

6. Длина ломаной EFMO равна 7 см (1, 2).

7. Длина отрезка ЕО должна быть не больше 7 см (4, 5).

8. Длина отрезка ЕО может быть равна 0,5 см, но не может быть равна 8 см (1, 2, 7).

Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:

Смотрите также дополнительные лекции по предмету «Математика»:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник