Что такое длина нулевого вектора

Определение вектора

В статье пойдет речь о том, что такое вектор, что он из себя представляет в геометрическом смысле, введем вытекающие понятия.

Для начала дадим определение:

Вектор – это направленный отрезок прямой.

Исходя из определения, под вектором в геометрии отрезок на плоскости или в пространстве, который имеет направление, и это направление задается началом и концом.

Нулевой вектор

Под нулевым вектором 0 → будем понимать любую точку плоскости или пространства.

Из определения становится очевидным, что нулевой вектор может иметь любое направление на плоскости и в пространстве.

Длина вектора

Под длиной вектора A B → понимается число, большее либо равное 0, и равное длине отрезка АВ.

Понятия модуль вектора и длина вектора равносильны, потому что его обозначение совпадает со знаком модуля. Поэтому длину вектора также называют его модулем. Однако грамотнее использовать термин «длина вектора». Очевидно, что длина нулевого вектора принимает значение ноль.

Коллинеарность векторов

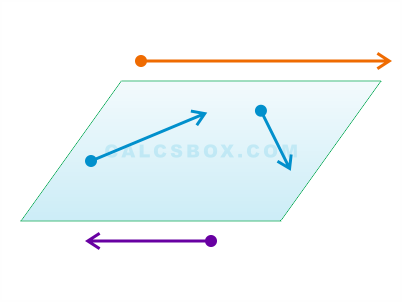
Два вектора лежащие на одной прямой или на параллельных прямых называются коллинеарными.

Два вектора не лежащие на одной прямой или на параллельных прямых называются неколлинеарными.

Следует запомнить, что Нулевой вектор всегда коллинеарен любому другому вектору, так как он может принимать любое направление.

Коллиниарные векторы в свою очередь тоже можно разделить на два класса: сонаправленные и противоположно направленные.

Направление векторов

Считается, что нулевой вектор является сонаправленым к любым другим векторам.

Равные и противоположные векторы

Равными называются сонаправленные вектора, у которых длины равны.

Противопожными называются противоположно направленные вектора, у которых их длины равны.

Введенные выше понятия позволяют нам рассматривать векторы без привязки к конкретным точкам. Иначе говоря, можно заменить вектор равным ему вектором, отложенным от любой точки.

Углы между векторами

Угол φ = ∠ A O B называется углом между векторами a → = O A → и b → = O B → .

Очевидно, что угол между сонаправленными векторами равен нулю градусам (или нулю радиан), так как сонаправленные векторы лежат на одной или на параллельных прямых и имеют одинаковое направление, а угол между противоположно направленными векторами равен 180 градусам (или π радиан), так как противоположно направленные векторы лежат на одной или на параллельных прямых, но имеют противоположные направления.

Перпендикулярными называются два вектора, угол между которыми равен 90 градусам (или π 2 радиан).

Источник

Вектор. Определение и основные понятия

Обозначение вектора

Направление вектора (от начала к концу) на рисунках отмечается стрелкой.

Длина вектора

Нулевой вектор

Длина нулевого вектора равна нулю.

Любая точка пространства также может рассматриваться как вектор. Такой вектор называется нулевым. Начало и конец нулевого вектора совпадают, и он не имеет какого-либо определенного направления.

Нулевым вектором называется вектор, у которого начальная и конечная точка совпадают.

Длина вектора на плоскости

Длина вектора в трехмерном пространстве

Длина вектора в n-мерном пространстве

Коллинеарные вектора

Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами

Сонаправленные вектора

Противоположно направленные вектора

Компланарные вектора

Вектора, параллельные одной плоскости или лежащие на одной плоскости называют компланарными векторами.

Равные вектора

То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:

Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!

О сайте

На нашем сайте вы найдете множество полезных калькуляторов, конвертеров, таблиц, а также справочных материалов по основным дисциплинам.

Самый простой способ сделать расчеты в сети — это использовать подходящие онлайн инструменты. Воспользуйтесь поиском, чтобы найти подходящий инструмент на нашем сайте.

calcsbox.com

На сайте используется технология LaTeX.
Поэтому для корректного отображения формул и выражений
пожалуйста дождитесь полной загрузки страницы.

© 2021 Все калькуляторы online

Копирование материалов запрещено

Источник

Вычислительная геометрия, или как я стал заниматься олимпиадным программированием.Часть 1

Здравствуйте, уважаемые хабравчане! Это моя вторая статья, и мне хотелось бы поговорить о вычислительной геометрии.

Немного истории

Я являюсь студентом уже 4 курса математического факультета, и до того как я начал заниматься программированием, я считал себя математиком на 100 процентов.

В конце первого курса мой преподаватель по информатике, который занимается олимпиадным программированием, обратил на меня внимание. Им как раз не хватало одного математика в команду. Так потихоньку меня начали приучать к олимпиадному программированию. Скажу честно, для меня это было очень сложно: для человека, который узнал слово Delphi на первом курсе. Однако мой преподаватель оказался очень грамотным специалистом и нашел хороший подход ко мне. Он начал давать мне математические задачи, который я сначала решал чисто математически, а уже потом писал код (с грехом пополам).

Мне очень нравится подход моего преподавателя: «разберись с этой темой, а потом расскажи нам, да так чтоб мы все поняли».

Итак, первой на самом деле важной задачей, с которой мне поручили разобраться, было именно вычислительная геометрия, необходимо было разобраться в типичных задач этого раздела информатики. И я решил подойти к этой задаче со всей ответственностью.

Я помню, как долго мучился с этими задачами, чтобы они прошли все тесты на сайте informatics.mccme. Зато теперь я очень рад, что прошел через все испытания и знаю, что же такое задачи вычислительной геометрии.

Вступление

«Вычислительная геометрия – это раздел информатики, изучающий алгоритмы решения геометрических задач. Такие задачи возникают в компьютерной графике, проектировании интегральных схем, технических устройств и др. Исходными данными в такого рода задачах могут быть множество точек, набор отрезков, многоугольники и т.п. Результатом может быть либо ответ на какой-то вопрос, либо какой-то геометрический объект».

Поскольку статья является достаточно большой я решил разбить ее на две части: первая часть посвящена многоугольникам, вторая – взаимному расположению различных геометрических объектов.

Немного теории о векторах

Отрезок, для которого указано, какой из его концов считается началом, а какой — концом, называется вектором. Любая точка пространства также может рассматриваться как вектор. Такой вектор называется нулевым. Начало и конец нулевого вектора совпадают, и он не имеет какого-либо определенного направления.

Длиной ненулевого вектора AB называется длина отрезка AB. Длина нулевого вектора считается равной нулю.
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Если два ненулевых вектора AB и CD коллинеарны и если при этом лучи AB и CD сонаправлены, то векторы AB и CD называются сонаправленными, а если эти лучи не являются сонаправленными, то векторы AB и CD называются противоположно направленными. Нулевой вектор принято считать сонаправленным с любым вектором.

Скалярное произведение векторов

Скалярное произведение векторов — это число, равное произведению длин этих векторов на косинус угла между ними.
(a, b) = |a||b|cos∠(a, b)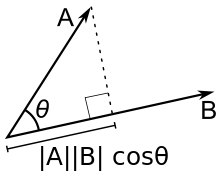

Если векторы заданы своими координатами a(x₁, y₁), b(x₂, y₂) то скалярное произведение (a, b) = x₁x₂ + y₁y₂.

Косое произведение векторов

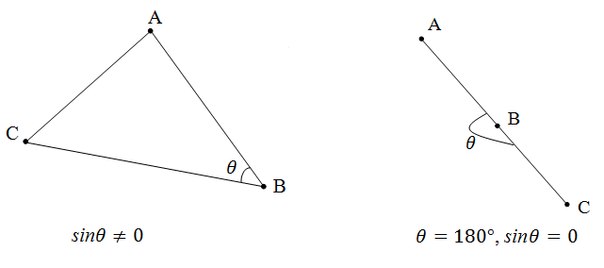
Псевдоскалярным или косым произведением векторов на плоскости называется число
[a, b] = |a||b|sinθ
где — угол вращения (против часовой стрелки) от a к b. Если хотя бы один из векторов a и b нулевой, то полагают [a, b] = 0.
Если векторы заданы своими координатами a(x₁, y₁), b(x₂, y₂) то косое произведение [a, b] = x₁y₂ — x₂y₁.
Геометрически косое произведение векторов представляет собой ориентированную площадь параллелограмма, натянутого на эти вектора.

Косое произведение векторов в задачах вычислительной геометрии занимает такое же почетное место, как рекурсии в комбинаторике. Это своего рода жемчужина вычислительной геометрии. Практически каждая задача вычислительной геометрии имеет более простое решение с помощью косового произведение вместо лобового решения.

А теперь займемся практикой

Начнем с треугольников

Задача №1

Задача очень простая, а именно: по введенным трем числам a, b, c определить существует ли треугольник с такими сторонами.

Решение
Понятно, что здесь нужно только проверить неравенство треугольника: a + b > c, a + c > b, b + c > a. Интересно, при изучении неравенства треугольника только ли у меня возник вопрос: не могут ли отрицательные числа тоже удовлетворять этим трем неравенствам? Оказывается, нет! Если мы сложим каждое неравенство, то получим a > 0, b > 0, c > 0. Поэтому неравенство треугольника является необходимым и достаточным условием существования треугольника.

Задача №2

Задача является очень похожей на предыдущую с той разницей, что треугольник задан не сторонами, а координатами вершин.

Решение
С первого взгляда решение кажется очевидным: вычислить стороны треугольника и свести задачу к предыдущей. Однако поскольку расстояние между двумя точками A(x₁, y₁), B(x₂, y₂) вычисляется по формуле √(x₁-x₂) 2 +(y₁-y₂) 2 то при извлечении корня возможна потеря точности, что плохо скажется на проверке неравенства треугольника. Оказывается, что если треугольник задан координатами своих вершин, то вычислять длины его сторон и проверять неравенство треугольника не требуется. В этом случае треугольника не существует тогда и только тогда, когда данные три точки лежат на одной прямой. А это легко проверяется через косое произведение векторов. Если оно равно нулю, то векторы коллинеарные, то есть все три точки лежат на одной прямой.

Во всех следующих задачах будем считать, что треугольник существует, поскольку процедуру проверки существования треугольника мы только что рассмотрели.

Задача №3

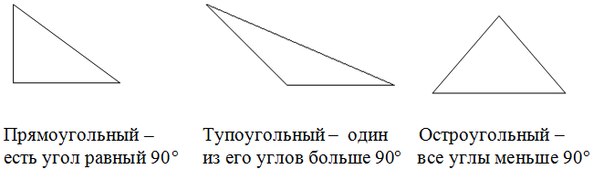
Треугольник задан своими сторонами. Определить тип треугольника: тупоугольный, прямоугольный или остроугольный.

Решение
Вспомним, что представляют собой каждый вид треугольника.

Задача №4

Задача аналогична предыдущей задаче, только треугольник задан не своими сторонами, а координатами вершин.

Решение
Аналогично задаче 2 можно сказать, что эта задача полностью сводится к предыдущей задаче (так оно и есть). Однако, как и во второй задаче, решение можно упростить. Вообще, если треугольник задан координатами своих вершин, то всегда легче работать с ним через вектора, нежели вычислять стороны. Аналогично предыдущей задаче, необходимо определить каким является наибольший из углов треугольника. Вид угла легко определяется по знаку скалярного произведения образующих его векторов: оно положительно для острого угла, равно нулю для прямого угла и отрицательно для тупого угла. Поэтому необходимо посчитать все три скалярных произведения и перемножить их и по знаку данного числа можно судить о типе треугольника.

Задача №5

По данным сторонам треугольника найти его площадь.

Решение
Очевидно решение, заключается в применение формулы Герона.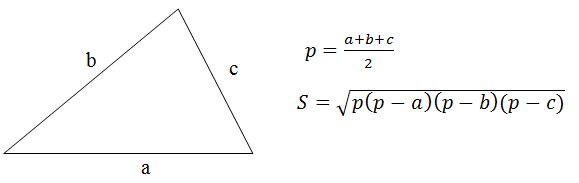

Кстати, никого не интересовало доказательство этой формулы?

Задача №6

Вычислить площадь треугольника заданного координатами своих вершин.

Решение
Не будем говорить о решении, которое сводится к предыдущей задачи, а попробуем воспользоваться геометрическим смыслом косового произведения. Геометрически косое произведение двух векторов определяет ориентированную площадь параллелограмма натянутого на эти вектора. Поскольку диагональ параллелограмма разбивает его на два равновеликих треугольника, то можем найти площадь нашего треугольника, как половину площади параллелограмма.
Для векторов a(x₁, y₁), b(x₂, y₂)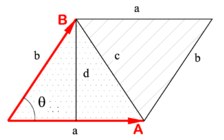

S = (x₁y₂ — x₂y₁) / 2 — ориентированная площадь треугольника

Задача №7

Дана точка и треугольник заданный координатами своих вершин. Определить лежит ли точка внутри, на границе или вне этого треугольника.

Решение
У этой задачи есть два принципиально разных решения. Начнем с наименее привлекательного.

Метод площадей

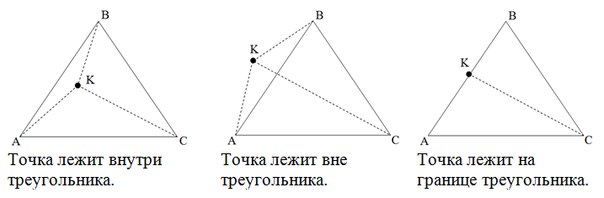
Если сумма площадей треугольников AKB, AKC, BKC (не ориентированных, а «обычных») больше площади треугольника ABC точка лежит вне треугольника. Если же сумма первых трех площадей равна четвертой, то нужно проверить, не равна ли нулю одна из трех площадей. Если равна, то точка лежит на границе треугольника, иначе – внутри.
Вычислять площади треугольников, естественно, надо через косое произведение векторов. Этот метод не очень хороший. Поскольку здесь используются сравнение чисел с плавающей точкой, а это в свою очередь может привести к принятию неверного решения при сравнении. Второй метод опять таки опирается на вектора, он намного эффективнее во всех отношениях.

Проверка полуплоскостей

Если хотя бы одна из сторон треугольника «разводит» противолежащую ей вершину и точку по разным полуплоскостям, то точка лежит вне треугольника. Иначе, если точка принадлежит хотя бы одной из прямых, содержащих стороны треугольника, то она находится на границе треугольника. Иначе точка лежит внутри треугольника.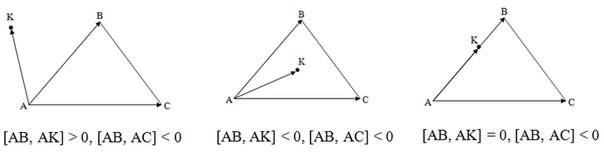

В первом примере сторона AB разводит вершину C и точку K по разным полуплоскостям, поэтому точка лежит снаружи.

Задача №8

Вычисление площади многоугольника заданного координатами своих вершин.

Решение
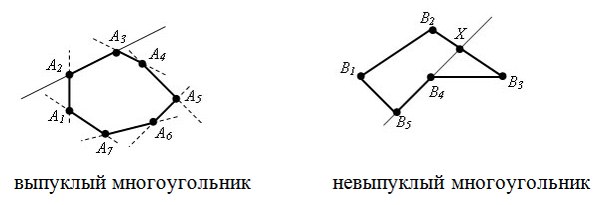
Под многоугольником будем подразумевать простой многоугольник, то есть без самопересечений. При этом он может быть как выпуклым, так и не выпуклым.

Данную задачу можно решить двумя способами: вычисляя ориентированные площади трапеций и треугольников.

Метод трапеций

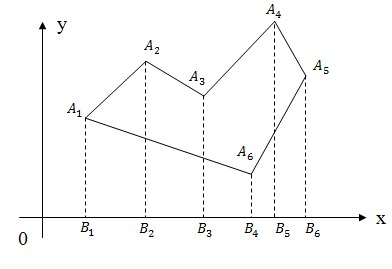
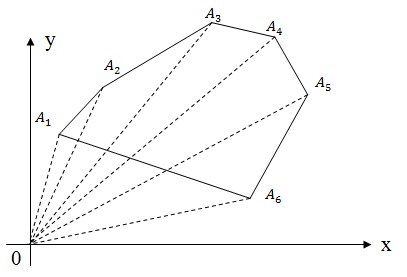
Для того чтобы посчитать площадь многоугольника нужно разбить его на трапеции, так как это показано на рисунке, а затем сложить ориентированные площади полученных трапеций это будет ориентированной площадью исходного многоугольника.
S = S_{A1 A2 B2 B1} + S_{A2 A3 B3 B2} + S_{A3 A4 B5 B3} + S_{A4 A5 B6 B5} + S_{A5 A6 B4 B6} + S_{A6 A1 B1 B4}
Площади трапеций считаем по известной формуле: полусумма оснований на высоту
S_{A1 A2 B2 B1} = 0.5 * (A₁B₁ + A₂B₂) *(B₂ — B₁)

Поскольку полученная площадь является ориентированной, необходимо вычислить ее модуль.

Метод треугольников

Как вы видите задача вычисления площади многоугольника достаточна проста. Не знаю, почему, но мне больше нравится решать эту задачу методом разбиения на трапеции (наверно потому, что на всех олимпиадах я ее так решал). Тем более, что при втором решении площади треугольников надо вычислять через косое произведение. О формуле Герона надо забыть.

Задача №9

Многоугольник задан координатами своих вершин в порядке его обхода. Необходимо проверить является ли многоугольник выпуклым.

Решение
Напомню, что многоугольник называется выпуклым, если он лежит в одной полуплоскости относительно любой прямой, содержащей его сторону.

Задача опять сводится к вычислению косового произведения векторов, а именно у выпуклого многоугольника знаки косых произведений [A_i A_i+1, A_i+1 A_i+2] либо положительны, либо отрицательны. Поэтому если мы знаем направление обхода, то знак косых произведений для выпуклого многоугольника одинаков: он неотрицателен при обходе против часовой стрелки и неположителен при обходе по часовой стрелки.

Задача №10

Многоугольник (не обязательно выпуклый) на плоскости задан координатами своих вершин. Требуется подсчитать количество точек с целочисленными координатами, лежащих внутри него (но не на его границе).

Решение
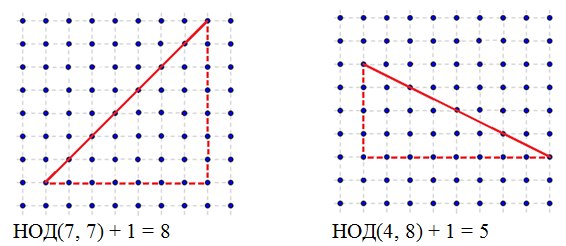
Для решения этой задачи рассмотрим вспомогательную задачу: отрезок задан координатами своих концов, являющихся целыми числами. Необходимо посчитать количество целочисленных точек лежащих на отрезке. Понятно, что если отрезок вертикальный или горизонтальный, то необходимо вычесть координаты концов и добавить единицу. Интерес представляет случай, когда отрезок не является вертикальным или горизонтальным. Оказывается в этом случае необходимо достроить отрезок до прямоугольного треугольника и ответом будет число равное наибольшему общему делителю длин катетов этого треугольника плюс единица.

Для любого многоугольника с целочисленными координатами вершин справедлива формула Пика: S = n + m/2 — 1, где S – площадь многоугольника, n – количество целых точек лежащих строго внутри многоугольника, m – количество целых точек лежащих на границе многоугольника. Поскольку площадь многоугольника мы знаем как вычислять, то S известно. Так же мы можем вычислить количество целых точек лежащих на границе многоугольника, поэтому в формуле Пика остается лишь одна искомая неизвестная которую мы можем найти.
Рассмотрим пример: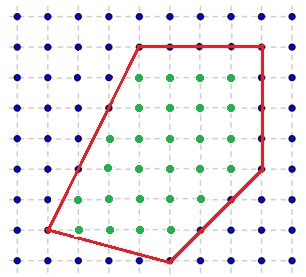

S = 16 + 4 + 4,5 + 6 + 1 + 2 = 33,5
m = 15
n = 33,5 – 7,5 +1 = 27 — точек лежит строго внутри многоугольника
Вот так вот решается эта задачка!

Вот и все! Надеюсь, Вам понравилась статья, и я напишу ее вторую часть.

Источник

Что такое вектор: определение, обозначение, виды

В данной публикации мы рассмотрим, что такое вектор, как он обозначается, а также какие виды бывают. Теоретическую информацию сопроводим рисунками для лучшего восприятия.

Определение вектора

Вектор – это направленный отрезок. Другими словами, это отрезок определенной длины, который направлен в конкретную сторону.

У вектора есть начало и конец. На рисунке ниже – это точки A и B, соответственно. Направление вектора показывается соответствующей стрелкой.

Примечание: нахождение длины вектора (| AB | или | a |) мы подробно рассмотрели в отдельной публикации.

Виды векторов

2. Единичный – вектор, длина которого равна единице. Также называется ортом.

3. Коллинеарные – векторы лежат на одной и той же или на параллельных прямых.

4. Сонаправленные – коллинеарные векторы, направления которых совпадает. Например, на рисунке ниже a и b являются сонаправленными.

5. Противоположно направленные – коллинеарные векторы, направления которых противоположны.

6. Компланарные – векторы, параллельные одной плоскости или лежащие на одной плоскости.

Примечание: любые два вектора компланарны, так как всегда найдется плоскость, параллельная им обоим.

7. Равные – векторы, имеющие одинаковую длину и направление, а также лежащие на одной или параллельных прямых.

Примечание: для вектора AB в произвольной точке C пространства удастся построить только один единственный вектор (например, CD ) той же длины.

Источник

Что такое длина нулевого вектора

1. Основные определения

Вектор пред­ставляет собой направленный отрезок прямой, для которого определены правила (законы) сложения с другими векторами, правило вычитания векторов, правило умножения вектора на число, скалярное произведение двух векторов и некоторые другие операции.

Число, выражающее длину направленного отрезка, называют модулем вектора и обозначают той же буквой, что и сам вектор, но без стрелки наверху, например: модулем вектора `vec v` является число `v`. Часто для обозначения модуля вектора прибегают к помощи знака абсолютной величины и пишут, например, `|vec v|` или `|vec F|`.

Вектор называется нулевым, если его начало и конец совпадают. Нулевой вектор не имеет определённого направления и его длина (модуль) равна нулю.

Векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых. Так, например, на рис. 3 векторы `vec a`, `vec b` и `vec c` коллинеарны.

Два вектора называются равными, если они коллинеарны, имеют одинаковую длину и одинаковое направление.

В физике точка приложения вектора иногда имеет принципиальное значение. Достаточно вспомнить рычаг: две равные по модулю силы, направленные в одну и ту же сторону, производят на рычаг разное действие, если плечи сил не равны друг другу. И всё же сами силы равны друг другу! Бывают и случаи, когда вектору трудно приписать конкретную точку приложения. Например, если одна система отсчёта движется относительно другой со скоростью `vec v`, то какой точке приписать эту скорость? Всем точкам движущейся системы!

2. Сложение двух векторов.

Пусть даны два произвольных вектора `vec a` и `vec b` (рис. 5а).

Описанное правило есть просто определение суммы векторов. Как и в случае с числами, сумма векторов не зависит от порядка слагаемых, и поэтому можно записать

Оба способа сложения дают идентичный результат и одинаково часто применяются на практике. Когда речь идёт о нахождении суммы трёх и более векторов, часто последовательно используют правило треугольника. Поясним сказанное.

3. Сложение трёх и более векторов.

Пусть нужно сложить три вектора `vec a`, `vec b` и `vec d` (рис. 6).

Для этого по правилу треугольника сначала находится сумма любых двух векторов, например `vec a` и `vec b`, потом полученный вектор `vec c = vec a + vec b` по тому же правилу складывается с третьим вектором `vec d`. Тогда полученный вектор `vec f = vec c + vec d` и будет представлять собой сумму трёх векторов `vec a`, `vec b` и `vec d`: `vec f = vec a + vec b + vec d`. Как и в случае с двумя векторами, порядок слагаемых не влияет на конечный результат.

Так, на рис. 7 вектор `vec g` представляет собой сумму векторов `vec a`, `vec b`, `vec d`, `vec e`, найденную по правилу многоугольника: `vec g = vec a + vec b + vec d + vec e`.

Не всякая векторная сумма может иметь физический смысл. Не всякие величины вообще имеет смысл складывать. Так, например, бессмысленно говорить, что, если у меня температура `36,6^@` и у вас тоже `36,6^@`, то вместе у нас температура `73,2^@`, хотя складывать температуры (числа) никто не запрещает. Всё же чаще всего сумма температур представляет собой никому не нужную величину; она редко входит в какие-либо уравнения (входит почти случайно).

Иное дело – с массой. Если система состоит из тел с массами `m_1`, `m_2`, `m_3` и т. д., то масса всей системы равна `m = m_1 + m_2 + m_3 + ` и т. д. (Если на лифте написано, что максимальный груз, перевозимый лифтом, равен `500` кг, то перед входом в лифт нужно убедиться, что сумма масс вносимых в лифт грузов не превышает `500` кг.) Говорят, что масса – есть аддитивная величина (от английского слова add – добавлять, прибавлять, складывать). А вот температура – не аддитивная величина.

В последнем равенстве мы встречаемся с умножением вектора на скаляр. Поясним эту процедуру.

4. Умножение вектора на скаляр.

Произведением вектора `vec a` на число `k` называют новый вектор `vec b = k vec a`, коллинеарный вектору `vec a`, направленный в ту же сторону, что и вектор `vec a`, если `k > 0`, и в противоположную сторону, если `k

Источник