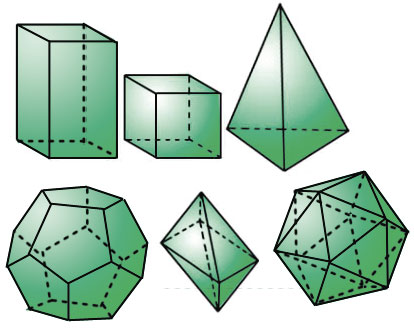
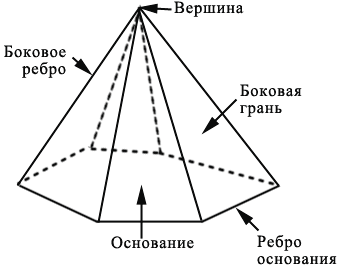
Что такое длина ребра
Что такое куб: определение, свойства, формулы
В публикации мы рассмотрим определение и основные свойства куба, а также формулы, касающиеся данной геометрической фигуры (расчет площади поверхности, периметра ребер, объема, радиуса описанного/вписанного шара и т.д.).
Определение куба
Куб – это правильный многогранник, все грани которого являются квадратами.
Примечание: куб является частным случаем параллелепипеда или призмы.
Свойства куба
Свойство 1
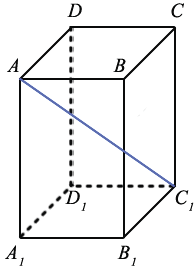
Как следует из определения, все ребра и грани куба равны. Также противоположные грани фигуры попарно параллельны, т.е.:
Свойство 2
Диагонали куба (их всего 4) равны и в точке пересечения делятся пополам.
Свойство 3
Все двугранные углы куба (углы между двумя гранями) равны 90°, т.е. являются прямыми.
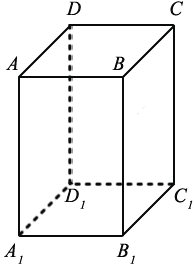
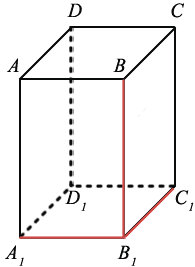
Например, на рисунке выше угол между гранями ABCD и AA1B1B является прямым.
Формулы для куба
Примем следующие обозначения, которые будут использоваться далее:
Диагональ
Длина диагонали куба равняется длине его ребра, умноженной на квадратный корень из трех.
Диагональ грани
Диагональ грани куба равна его ребру, умноженному на квадратный корень из двух.
Площадь полной поверхности
Площадь полной поверхности куба равняется шести площадям его грани. В формуле может использоваться длина ребра или диагонали.
Периметр ребер
Периметр куба равен длине его ребра, умноженной на 12. Также может рассчитываться через диагональ.
Объем
Объем куба равен длине его ребра, возведенной в куб.
Радиус описанного вокруг шара
Радиус шара, описанного около куба, равняется половине его диагонали.
Радиус вписанного шара
Радиус вписанного в куб шара равен половине длины его ребра.
Пример 2. Даны координаты вершин пирамиды ABCD: A(10;6;6), B(-2;8;2), C(6;8;9), D(7;10;3).
Угол между ребрами АВ и АD;
Уравнение прямой АВ;
Уравнение плоскости АВС;
Угол между ребром АD и гранью АВС;
Уравнение высоты, опущенной из вершины D на грань АВС.
Из пункта 1) нам известны координаты вектора =(-12;2;-4). Угол между двумя векторами находится по формуле:
Если векторы и имеют координаты =(х1;у1:z1), (х2;у2:z2) соответственно, то эта формула перепишется в виде:
3) Уравнение прямой, проходящей через две точки М1(х1;у1;z1) и М2(х2;у2;z2) имеет вид:
или равносильное ему уравнение:
где =(l,m,n) – координаты направляющего вектора прямой М1М2.
Направляющий вектор прямой – это вектор, параллельный прямой. В нашем случае прямая проходит через точки А(10;6;6) и В(-2;8;2).Следовательно, уравнение прямой АВ:
Итак, каноническое уравнение прямой АВ:
где направляющий вектор
4) Уравнение плоскости по трем точкам находится по формуле:
Считаем определитель, разложив его по первой строке.
Итак, уравнение плоскости АВС:
5) Требуется найти угол между ребром АD и гранью АВС. Это равносильно нахождению угла между прямой АD и плоскостью АВС. Угол между прямой и плоскостью Ах+Ву+Сz+D=0 определяется по формуле:
— координаты направляющего вектора прямой АD.
Находим уравнение прямой АD по двум точкам:
находим длину полученного вектора:
Куб — свойства, виды и формулы
Среди многогранников куб – это один из наиболее известных объектов, знакомых с далёкого детства. Более подробно эта тема изучается на уроках геометрии в старших классах, когда от фигур на плоскости переходят к телам в пространстве.
Кубу можно дать определение различными способами, каждый из которых только подчеркнёт тот или иной класс тел в пространстве, выделит основные признаки и особенности:
многогранник, у которого все рёбра равны, а грани попарно перпендикулярны;
прямая призма, все грани которой есть квадраты;
прямоугольный параллелепипед, все рёбра которого равны.
Всеми этими и многими другими подобными формулировками геометрия позволяет описывать одну и ту же фигуру в пространстве.
Элементы куба
Основными элементами многогранника считаются грани, рёбра, вершины.
Грань
Плоскости, образующие поверхность куба, называются гранями. Другое название – стороны.
Интересно, сколько граней у куба и каковы их особенности. Всего граней шесть. Две из них, параллельные друг другу, считаются основаниями, остальные – боковыми.
Грани куба попарно перпендикулярны, являются квадратами, равны между собой.
Ребро
Линии пересечения сторон называются рёбрами.
Не каждый школьник может ответить, сколько рёбер у куба. Их двенадцать. Они имеют одинаковые длины. Те из них, что обладают общим концом, расположены под прямым углом по отношению к любому из двух остальных.
Рёбра могут пересекаться в вершине, быть параллельными. Не лежащие в одной грани ребра, являются скрещивающимися.
Вершина
Точки пересечения рёбер называются вершинами. Их число равно восьми.
Центр грани
Отрезок, соединяющий две вершины, не являющийся ребром, называется диагональю.
Пересечение диагоналей грани считается центром грани – точкой, равноудалённой от всех вершин и сторон квадрата. Это есть центр симметрии грани.
Центр куба
Пересечение диагоналей куба является его центром – точкой, равноудалённой от всех вершин, рёбер и сторон многогранника.
Это есть центр симметрии куба.
Ось куба
Рассматриваемый многогранник имеет несколько осей ортогональной (под прямым углом) симметрии. К ним относятся: диагонали куба и прямые, проходящие через его центр параллельно рёбрам.
Диагональ куба
Отрезок, соединяющий две вершины, не принадлежащие одной стороне, называется диагональю рассматриваемого многогранника.
Учитывая, что ребра куба имеют равные измерения a, можно найти длину диагонали:
Формула доказывается с помощью дважды применённой теоремы Пифагора.
Диагональ куба — одна из осей симметрии.
Все диагонали куба равны между собой и точкой пересечения делятся пополам.
Диагональ грани куба
Длина диагонали грани в √2 раз больше ребра, то есть:
Эта формула доказывается также с помощью теоремы Пифагора.
Объем куба
Как для любого параллелепипеда, объём куба равен произведению всех трёх измерений, которые в данном случае равны:
Периметр куба
Сумма длин всех рёбер равна:
Площадь поверхности
Сумма площадей всех граней называется площадью поверхности куба. Она равна:
Сфера, вписанная в куб
Такая сфера имеет центр, совпадающий с центром куба.
Радиус равен половине ребра:
Сфера, описанная вокруг куба
Как для вписанной сферы, центр совпадает с точкой пересечения диагоналей, радиус равен половине диагонали:
Координаты вершин куба
В зависимости от расположения фигуры в системе координат, можно по-разному рассчитывать координаты вершин.
Наиболее часто используют следующий способ. Одна из вершин совпадает с началом координат, рёбра параллельны осям координат или совпадают с ними, координаты единичного куба в этом случае будут равны:
Такое расположение удобно для введения четырёхмерного пространства (вершины задаются всеми возможными бинарными наборами длины 4).
Свойства куба
Плоскость, рассекающая куб на две части, есть сечение. Его форма выглядит как выпуклый многоугольник.
Построение сечений необходимо для решения многих задач. Как правило, используется метод следов или условие параллельности прямых и плоскостей.
у куба все грани равны, являются квадратами;
у куба все рёбра равны;
один центр и несколько осей симметрии.
Прямоугольный параллелепипед. Пирамида.
| Площадью поверхности параллелепипеда называют сумму площадей всех его граней. |
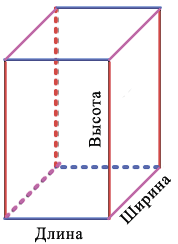
Измерения имеют названия: длина, ширина, высота. Данные названия введены, чтобы различать измерения:
Частным случаем прямоугольного параллелепипеда является куб. Куб — это прямоугольный параллелепипед, все измерения которого равны:
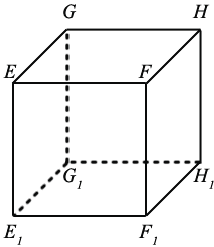
EFHGE1F1H1G1 — куб, его высота, ширина и длина равны. Гранями куба являются 6 равных квадратов.
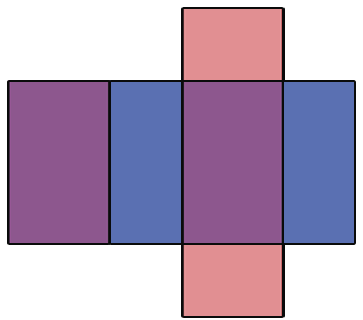
Рассмотрим следующую фигуру:
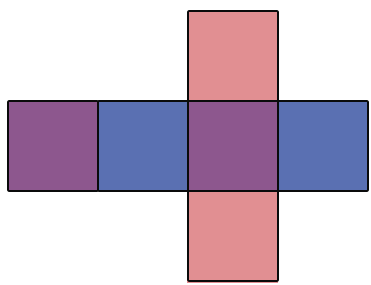
Данная фигура состоит из шести прямоугольников, которые попарно равны (выделены одним цветом). Если мы согнём по линиям данную фигуру и склеим, то получим модель прямоугольного параллелепипеда, противоположные грани которого будут одного цвета. Рассматриваемую фигуру называют развёрткой прямоугольного параллелепипеда. Как сказано выше, куб состоит из 6 равных квадратов, значит, его развертка будет иметь следующий вид:
В данном случае куб «разрезали» по 6 горизонтальным ребрам и 1 вертикальному, при этом противоположные грани выделены одним цветом. Таким образом, «разрезая» любой многогранник по ребрам так, чтобы все грани оказались в одной плоскости, можно получить его развертку. Развертки многогранников нужны, например, для создания их объемных моделей.
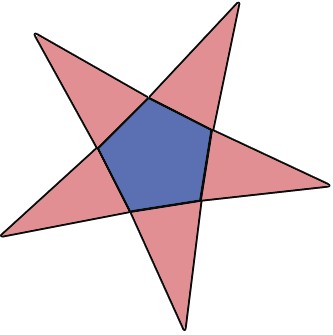
Если мы «разрежем» по боковым рёбрам пятиугольную пирамиду, то получим следующий многоугольник, который будет являться развёрткой данной пирамиды:
Поделись с друзьями в социальных сетях:
Ребро (геометрия)
Связанные понятия
Правильные четырёхмерные многогранники являются четырёхмерными аналогами правильных многогранников в трёхмерном пространстве и правильных многоугольников на плоскости.
Упоминания в литературе
Связанные понятия (продолжение)
Пра́вильный двадцатичетырёхъяче́йник, или просто двадцатичетырёхъяче́йник, или икоситетрахор (от др.-греч. εἴκοσι — «двадцать», τέτταρες — «четыре» и χώρος — «место, пространство»), — один из правильных многоячейников в четырёхмерном пространстве.
Пра́вильный шестнадцатияче́йник, или просто шестнадцатияче́йник — один из правильных многоячейников в четырёхмерном пространстве. Известен также под другими названиями: гексадекахор (от др.-греч. ἕξ — «шесть», δέκα — «десять» и χώρος — «место, пространство»), четырёхмерный гиперокта́эдр (поскольку является аналогом трёхмерного октаэдра), четырёхмерный кокуб (поскольку двойственен четырёхмерному гиперкубу), четырёхмерный ортоплекс.
В геометрии политоп (многогранник, многоугольник или замощение, например) изогонален или вершинно транзитивен, если, грубо говоря, все его вершины эквивалентны. Отсюда следует, что все вершины окружены одним и тем же видом граней в том же самом (или обратном) порядке и с теми же самыми углами между соответствующими гранями.
Если дано топологическое пространство и группа действий на нём, образы отдельной точки под действием группы действий образуют орбиты действий. Фундаментальная область — это подмножество пространства, которое содержит в точности по одной точке из каждой орбиты. Она даёт геометрическую реализацию абстрактного множества представителей орбит.
Многогранник размерности 3 и выше называется изоэдральным или гране транзитивным, если все его грани одинаковы. Точнее сказать, все грани должны быть не просто конгруэнтны, а должны быть транзитивны, то есть должны прилежать в одной и той же орбите симметрии. Другими словами, для любых граней A и B должна существовать симметрия всего тела (состоящая из вращений и отражений), которая отображает A в B. По этой причине выпуклые изоэдральные многогранники имеют формы правильных игральных костей.
В геометрии фигуру называют хиральной (и говорят, что она обладает хиральностью), если она не совпадает со своим зеркальным отображением, точнее, не может быть совмещена с ним только вращениями и параллельными переносами. Хиральная фигура и её зеркальный образ называют энантиоморфами. Слово хиральность происходит от др.-греч. χειρ (хеир) — «рука». Это самый известный хиральный объект. Слово энантиоморф происходит от др.-греч. εναντιος (энантиос) — «противоположный», и μορφη (морфе) — «форма». Нехиральный.
Полуправильные многогранники — в общем случае это различные выпуклые многогранники, которые, не являясь правильными, имеют некоторые их признаки, например: все грани равны, или все грани являются правильными многоугольниками, или имеются определённые пространственные симметрии. Определение может варьироваться и включать различные типы многогранников, но в первую очередь сюда относятся архимедовы тела.
Пра́вильный пятияче́йник, или просто пятияче́йник, или пентахор (от др.-греч. πέντε — «пять» и χώρος — «место, пространство»), — один из правильных многоячейников в четырёхмерном пространстве: правильный четырёхмерный симплекс.