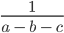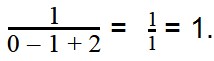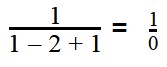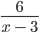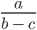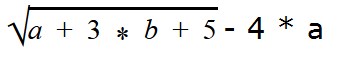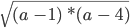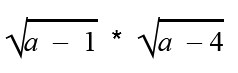Что такое допустимое значение переменной в алгебре 8 класс

Область допустимых значений (ОДЗ), теория, примеры, решения

Каждому выражению с переменными соответствует область допустимых значений (ОДЗ) переменных, которую ОБЯЗАТЕЛЬНО нужно учитывать при работе с этим выражением. Акцент на слове «обязательно» сделан не случайно: при решении примеров и задач халатное отношение к ОДЗ может привести к получению неверных результатов.

Чтобы у нас не возникало подобных проблем, давайте внимательно изучим все, что связано с ОДЗ. Для начала узнаем, что это такое, после этого разберем на характерных примерах, как найти ОДЗ переменных для заданного выражения, а в заключение остановимся на важности учета ОДЗ при преобразовании выражений.

Навигация по странице.

Допустимые и недопустимые значения переменных

Определение области допустимых значений переменных для выражения дается через термин допустимые значения переменной. Введем это вспомогательное определение, для чего проследим, что нас приводит к нему.

На уроках математики в школе вплоть до 7 класса познаются азы работы преимущественно с числами и числовыми выражениями. А с 7 класса начинается изучение такой математической дисциплины как алгебра, и начинается оно с того, что вводится определение выражения с переменными, а также связанное с ним определение значения выражения при выбранных значениях переменных.

выражение с переменными имеет смысл при данных значениях переменных, если при этих значениях переменных можно вычислить его значение

выражение с переменными не имеет смысла при данных значениях переменных, если при этих значениях переменных нельзя вычислить его значение.

Вот теперь мы обладаем всеми сведениями, позволяющими дать определение допустимых и недопустимых значений переменных:

Допустимые значения переменных – это такие значения переменных, при которых выражение имеет смысл. А значения переменных, при которых выражение не имеет смысла, называют недопустимыми значениями переменных.

Что такое ОДЗ?

Практически у всех, так или иначе имеющих отношение к алгебре, на слуху словосочетание «область допустимых значений», также довольно часто аббревиатуру ОДЗ можно встретить в описаниях решений, но как такового определения области допустимых значений (ОДЗ) нет в основных учебниках, используемых в школе. Поэтому интересно, откуда берет начало этот термин. Ну а с позиций практики интереснее знать, какой смысл в него вкладывают.

Под областью допустимых значений (ОДЗ) понимают множество всех допустимых значений переменных для данного выражения.

Как найти ОДЗ? Примеры, решения

Прежде чем обратиться к главной теме этого пункта, нужно понимать, что значит найти ОДЗ, хотя это достаточно отчетливо ясно из определения. Это значит, что надо указать множество всех допустимых значений переменных для заданного выражения. На это можно посмотреть и с другой стороны: найти ОДЗ – это значит указать условия, которые исключают те и только те значения переменных, при которых выражение не имеет смысла. Теперь можно двигаться дальше.

Заданий с формулировкой «найти ОДЗ» не так много. Однако почти постоянно приходится преобразовывать выражения, а это неявно требует нахождения области допустимых значений для ее контроля. В этом свете вопрос, как найти ОДЗ, очень злободневен.

В поисках ответа на него поразмыслим, значения каких выражений мы не можем вычислить.

Что нам это дает? А то, что перечисленные выше моменты и нужно учитывать при поиске ОДЗ. Как это делать, станет понятно из следующих примеров.

Найти ОДЗ переменной x для выражения .

Найти ОДЗ .

В более сложных случаях приходится учитывать одновременно несколько условий из приведенного выше списка. Это дает системы неравенств, задающие ОДЗ.

Определите ОДЗ переменной x для выражения .

Здесь лишь заметим, что во многих случаях на практике нет необходимости в решении составленных систем.

В заключении остается сказать, что такой подход используется и тогда, когда нужно найти область определения функции.

Почему важно учитывать ОДЗ при проведении преобразований?

Решая различные задачи, нам очень часто приходится проводить тождественные преобразования выражений. Но бывает, что какое-то преобразование в одних случаях допустимо, а в других – нет. Существенную помощь в плане контроля допустимости проводимых преобразований оказывает ОДЗ. Остановимся на этом подробнее.

Суть подхода состоит в следующем: сравниваются ОДЗ переменных для исходного выражения с ОДЗ переменных для выражения, полученного в результате выполнения тождественных преобразований, и на основании результатов сравнения делаются соответствующие выводы.

Вообще, тождественные преобразования могут

Давайте поясним каждый случай примером.

При преобразовании выражений надо строго избегать преобразований, сужающих ОДЗ. Почему? Для пояснения приведем пример.

Так что надо придерживаться таких тождественных преобразований выражения, которые не изменяют ОДЗ.

А как быть с преобразованиями выражений, при которых расширяется ОДЗ? Их можно проводить, но при этом стоит придерживаться такого взгляда: полученное в результате преобразования выражение рассматривать на ОДЗ переменных исходного выражения.

Итак, на каждом шаге преобразования выражения постоянно спрашивайте себя: «Не изменяет ли это преобразование ОДЗ»? Если не изменяет, то выполняйте его. Если сужает, то откажитесь от него. А если расширяет, то выполняйте его, но оставайтесь в рамках ОДЗ переменных для исходного выражения.

Источник

Урок по алгебре в 8 классе на тему: «Дроби. Дробные выражения. Рациональные выражения. Допустимые значения переменных».

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

МБОУ «Нововикринская СОШ».

Автор учитель математики Казумбекова Кистаман Магомедовна.

Урок по алгебре в 8 классе на тему: «Дроби. Дробные выражения. Рациональные выражения. Допустимые значения переменных».

Цель: добиться усвоения учащимися содержания понятий: целое выражение, дробное выражение, рациональное выражение, рациональное дробь, допустимые значения переменной в выражении; сформировать у учащихся умения выделять названные виды выражений среди предложенных выражений с переменными, а также выполнять действия, которые имеют целью нахождение ОДЗ дробного выражения.

Тип урока: усвоение знаний, умений и навыков.

Наглядность и оборудование: опорный конспект «Дробные выражения. Рациональные выражения».

I. Организационный этап

Вступительное слово учителя

· Особенности изучения алгебры в 8 классе;

· организация учебного процесса;

Учитель проверяет летнее домашнее задание (если такое было задано).

С целью осознания учащимися необходимости изучения вопроса о видах рациональных выражений предлагаем учащимся задание:

Какой из выражений: х2, х + 2ху, , лишний? Почему?

После обсуждения с учащимися результатов выполнения предложенного задания формируется мнение: в 7 классе был изучен вопрос о виды, свойства и способы преобразования выражений, не содержит деления на переменную (целые выражения); в 8 классе пришло время изучить виды, свойства и способы преобразований выражений, содержащих деление на переменную(дробные выражения), а также обобщить знания учащихся о видах выражений и логическую связь между ними. Этот вывод и является основной дидактической целью изучения раздела.

@ целях успешного восприятия учащимися учебного материала урока перед изучением новой темы следует активизировать знания учащихся о алгоритмы выполнения действий с рациональными числами, способы преобразования целых рациональных выражений и способы решения линейных уравнений и уравнений, сводящихся к линейным (изученные в 7 классе).

Выполнение устных упражнений

1. Найдите значения выражений:

2. Вычислите:
; ; ; ; ; ; 19 · 0,1; 7 : 0,1; ; .

5. Представьте выражения в виде произведения:

6. Преобразуйте выражения в многочлен стандартного вида:

План изучения нового материала

2. Дробные выражения.

3. Рациональные выражения.

4. Рациональный дробь.

5. Допустимые значения переменных в выражении (ОДЗ).

Дробные выражения. Рациональные выражения

1. Целые выражения состоят из чисел, букв и степеней и действий сложения, вычитания, умножения, возведения в степень и деления, кроме деления на переменную.

!Любое целое выражение можно представить в виде многочлена.

2. Дробные выражения обязательно содержащие действие деления на выражение с переменной (переменными), а также могут содержать все действия, которые есть в целом выражении.

3. Целые выражения вместе с дробными выражениями называют рациональными выражениями.

Пример. ; ; — рациональные дроби.

!Для рационального дроби допустимые значения переменной определяются из условия В ≠ 0 (знаменатель не должен равняться 0).

Итак, ОДЗ переменной а в выражении можно записать так:

6. Рациональный дробь равна 0, тогда и только тогда, когда А = 0 и В ≠ 0 (или )

Чтобы найти значение переменной, при котором рациональный дробь равна 0, надо:

а) найти ОДЗ дроби (из условия В ≠ 0);

б) приравнять числитель к нулю (А = 0) и найти соответствующие значения переменных;

в) из значений, полученных в п. б) исключить те, что не входящие в ОДЗ (см. п. а.).

Пример. При каком значении переменной дробь равна нулю?

@ Изучения материала урока начинается с повторения видов целых выражений, которые изучали ученики в 7 классе (одночлен, многочлены), и обобщение представлений учащихся об их структуру и свойства (все целые выражения содержат 5 арифметических действий, кроме деления на выражение с переменными, и могут быть представлены в виде многочлена).

Далее формируется представление учащихся о содержании понятия рационального дроби как особого случая дробного выражения и о содержании понятия допустимого значения переменной в выражении и области допустимых значений переменной (ОДЗ) в выражении (при этом можно опираться на приобретенные учащимися в 7 классе знания о содержании понятия области определения функции).

Выполнение устных упражнений

1. Какие из выражений являются целыми; дробными? Какие из выражений являются дробями; рациональными дробями?

а) ; б) ; в) ; г) ; д) ; е) .

3. При каких значениях переменной выражение не имеет смысла? Назовите допустимые значения переменной в выражении:

а) ; б) ; в) ; г) .

4. Какие из приведенных равенств является тождественностями?
а) ; б) ; в) .

Выполнение письменных упражнений

@ Для реализации дидактической цели на этом уроке следует решить задачи следующего содержания:

1. Среди представленных выражений с переменными выбрать: целые, дробные выражения, рациональные дроби.

1) Какие из выражений являются целыми; дробными? Какие из выражений являются дробями; рациональными дробями?

а) ; б) ; в) ; г) ; д) ; е) .

а) целыми выражениями; б) дробными выражениями.

2. Нахождение значения дробного выражения при данных значениях переменных.

1) Найдите значение выражения:

г) при b = 3;

д) при x = ;

есть) при в = 1,5.

2) Чему равно значение дроби при:

3. Нахождение допустимых значений переменных в выражении.

1) Укажите допустимые значения переменной в выражении:

а) ; б) ; в) ; г) .

2) Найдите допустимые значения переменной в выражении:

а) ; б) ; в) .

4. Составление выражений с переменными по условию задачи.

Автомобиль проехал 195 км за? ч. Запишите в виде выражения скорость автомобиля. Найдите значение этого выражения при t = 3. Выполнение упражнений на повторение: арифметические действия с обыкновенными дробями (сокращение, сравнение, сложение, вычитание, разложение целых выражений на множители с применением различных способов.

1) Преобразуйте в многочлен:

2) Разложите многочлен на множители:

3) Разложите на множители:

1) Какие выражения называют целыми? Приведите примеры.

2) Какие выражения называют дробными? Приведите примеры.

1. Изучить определения понятий, рассмотренных на уроке.

2. Решить упражнения на: классификацию рациональных выражений, нахождение ОДЗ выражений, вычисление значений выражений с переменными, числовых выражений, содержащих обыкновенные дроби, решение целых уравнений.

Источник

Область допустимых значений функции

Допустимые и недопустимые значения переменных

В 7 классе заканчивается математика и начинается ее-величество-алгебра. Первым делом школьники изучают выражения с переменными.

Мы уже знаем, что математика состоит из выражений — буквенных и числовых. Каждому выражению, в котором есть переменная, соответствует область допустимых значений (ОДЗ). Если игнорировать ОДЗ, то в результате решения можно получить неверный ответ. Получается, чтобы быстро получить верный ответ, нужно всегда учитывать область допустимых значений.

Чтобы дать верное определение области допустимых значений, разберемся, что такое допустимые и недопустимые значения переменной.

Рассмотрим все необходимые определения, связанные с допустимыми и недопустимыми значениями переменной.

Выражение с переменными — это буквенное выражение, в котором буквы обозначают величины, принимающие различные значения.

Значение числового выражения — это число, которое получается после выполнения всех действий в числовом выражении.

Выражение с переменными имеет смысл при данных значениях переменных, если при этих значениях переменных можно вычислить его значение.

Выражение с переменными не имеет смысла при данных значениях переменных, если при этих значениях переменных нельзя вычислить его значение.

Теперь, опираясь на данные определения, мы можем сформулировать, что такое допустимые и недопустимые значения переменной.

Допустимые значения переменных — это значения переменных, при которых выражение имеет смысл.

Если при переменных выражение не имеет смысла, то значения таких переменных называют недопустимыми.

В выражении может быть больше одной переменной, поэтому допустимых и недопустимых значений может быть больше одного.

Пример 1

Рассмотрим выражение

В выражении три переменные (a, b, c).

Запишем значения переменных в виде: a = 0, b = 1, c = 2.

Такие значения переменных являются допустимыми, поскольку при подстановке этих значений в выражение, мы легко можем найти ответ:

Таким же образом можем выяснить, какие значения переменных — недопустимые.

Подставим значения переменных в выражение

На ноль делить нельзя.

Что такое ОДЗ

ОДЗ — это невидимый инструмент при решении любого выражении с переменной. Чаще всего, ОДЗ не отображают графически, но всегда «держат в уме».

Область допустимых значений (ОДЗ) — это множество всех допустимых значений переменных для данного выражения.

Пример 2

Рассмотрим выражение

Пример 3
Рассмотрим выражение

ОДЗ такого выражения будет выглядеть вот так: b ≠ c; a — любое число.

Такая запись означает, что область допустимых значений переменных b, c и a = это все значения переменных, при которых соблюдаются условия b ≠ c; a — любое число.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Как найти ОДЗ: примеры решения

Найти ОДЗ — это значит, что нужно указать все допустимые значения переменных для выражения. Часто, чтобы найти ОДЗ, нужно выполнить преобразование выражения.

Чтобы быстро и верно определять ОДЗ, запомните условия, при которых значение выражения не может быть найдено.

Мы не можем вычислить значение выражения, если:

Теперь, приступая к поиску ОДЗ, вы можете сверять выражение по всем этим пунктам.

Давайте потренируемся находить ОДЗ.

Пример 4

Найдем область допустимых значений переменной выражения a 3 + 4 * a * b − 6.

В куб возводится любое число. Ограничений при вычитании и сложении нет. Это значит, что мы можем вычислить значение выражения a 3 + 4 * a * b − 6 при любых значениях переменной.

ОДЗ переменных a и b — это множество таких пар допустимых значений (a, b), где a — любое число и b — любое число.

Ответ: (a и b), где a — любое число и b — любое число.

Пример 5

Найдем область допустимых значений (ОДЗ) переменной выражения

Здесь нужно обратить внимание на наличие нуля в знаменатели дроби. Одним из условий, при котором вычисление значения выражения невозможно явлется наличие деления на ноль.

Это значит, что мы может сказать, что ОДЗ переменной a в выражении 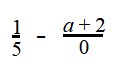— пустое множество.

Пустое множество изображается в виде вот такого символа Ø.

Пример 6

Найдем область допустимых значений (ОДЗ) переменных в выражении

Если есть квадратный корень, то нам нужно следить за тем, чтобы под знаком корня не было отрицательного числа. Это значит, что при подстановке значений a и b должны быть условия, при которых a + 3 * b + 5 ≥ 0.

Ответ: ОДЗ переменных a и b — это множество всех пар, при которых a + 3 * b + 5 ≥ 0.

Запомните

Например, если х > 6, но х

Зачем учитывать ОДЗ при преобразовании выражения

Иногда выражение просто невозможно решить, если не выполнить ряд тождественных преобразований. К ним относятся: перестановки, раскрытие скобок, группировка, вынесение общего множителя за скобки, приведение подобных слагаемых.

Кроме того, что видов таких преобразований довольно много: нужно понимать, в каких случаях какое преобразование возможно. В этом может помочь определение ОДЗ.

Тождественное преобразование может:

Рассмотрим каждый случай в отдельности.

Пример 7

Поскольку мы должны следить за тем, чтобы в выражении не возникало деление на ноль, определяем условие a ≠ 0.

Это условие отвечает множеству (−∞ ; 0) ∪ (0 ; +∞).

В выражении есть подобные слагаемые, если привести подобные слагаемые, то мы получаем выражение вида a.

ОДЗ для a — это R — множество всех вещественных чисел.

Преобразование расширило ОДЗ — добавился ноль.

Пример 8

Рассмотрим выражение a 2 + a + 4 * a

ОДЗ a для этого выражения — множество R.

В выражении есть подобные слагаемые, выполним тождественное преобразование.

После приведения подобных слагаемых выражение приняло вид a 2 + 5 * a

ОДЗ переменной a для этого выражения — множество R.

Это значит, что тождественное преобразование никак не повлияло на ОДЗ.

Пример 9

Рассмотрим выражение

Решить такое неравенство можно методом интервалов, что дает нам ОДЗ (−∞; 1] ∪ [4 ; +∞).

Затем выполним преобразование исходного выражения по свойству корней: корень произведения = произведению корней.

Приведем выражение к виду

Решив систему линейных неравенств, получаем множество [4; + ∞).

Отсюда видно, что тождественные преобразования сузили ОДЗ.
От (−∞; 1] ∪ [4 ; +∞) до [4; + ∞).

Решив преобразовать выражение, внимательно следите за тем, чтобы не допустить сужение ОДЗ.

Запомните, что выполняя преобразование, следует выбирать такие, которые не изменят ОДЗ.

Источник