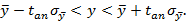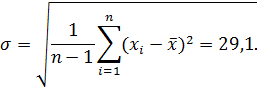Что такое доверительный интервал в физике
Доверительный интервал и доверительная вероятность



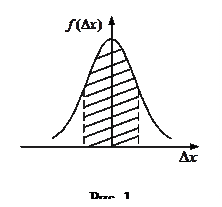
Для подавляющего большинства простых измерений достаточно хорошо выполняется так называемый нормальный закон случайных погрешностей (закон Гаусса), выведенный из следующих эмпирических положений.
1) погрешности измерений могут принимать непрерывный ряд значений;
2) при большом числе измерений погрешности одинаковой величины, но разного знака встречаются одинаково часто,
3) чем больше величина случайной погрешности, тем меньше вероятность ее появления.

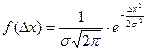
где 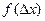


Величина σ не является случайной величиной и характеризует процесс измерений. Если условия измерений не изменяются, то σ остается постоянной величиной. Квадрат этой величины называют дисперсией измерений. Чем меньше дисперсия, тем меньше разброс отдельных значений и тем выше точность измерений.
Точное значение средней квадратичной ошибки σ, как и истинное значение измеряемой величины, неизвестно. Существует так называемая статистическая оценка этого параметра, в соответствии с которой средняя квадратичная ошибка равняется средней квадратичной ошибке среднего арифметического 
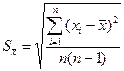
где 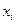
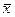
Чем больше число измерений, тем меньше 
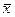

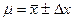
Интервал значений от 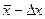
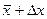

Все это справедливо для достаточно большого числа измерений, когда 
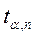


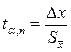
Функция распределения табулирована (табл.1). Значение коэффициента Стьюдента находится на пересечении строки, соответствующей числу измерений n, и столбца, соответствующего доверительной вероятности α
Таблица 1.
| n | α | n | α | ||||
| 0,8 | 0,9 | 0,95 | 0,98 | 0,8 | 0,9 | 0,95 | 0,98 |
| 1,9 | 2,9 | 4,3 | 7,0 | 1,5 | 2,0 | 2,6 | 3,4 |
| 1,6 | 2,4 | 3,2 | 4,5 | 1,4 | 1,9 | 2,4 | 3,1 |
| 1,5 | 2,1 | 2,8 | 3,7 | 1,4 | 1,9 | 2,4 | 3,9 |
Пользуясь данными таблицы, можно:
1) определить доверительный интервал, задаваясь определенной вероятностью;
2) выбрать доверительный интервал и определить доверительную вероятность.
При косвенных измерениях среднюю квадратичную ошибку среднего арифметического значения функции 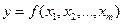
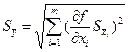
Доверительный интервал и доверительная вероятность определяются так же, как и в случае прямых измерений.
Доверительные интервалы
Определение
Доверительные интервалы (англ. Confidence Intervals) одним из типов интервальных оценок используемых в статистике, которые рассчитываются для заданного уровня значимости. Они позволяют сделать утверждение, что истинное значение неизвестного статистического параметра генеральной совокупности находится в полученном диапазоне значений с вероятностью, которая задана выбранным уровнем статистической значимости.
Нормальное распределение
Когда известна вариация (σ 2 ) генеральной совокупности данных, для расчета доверительных пределов (граничных точек доверительного интервала) может быть использована z-оценка. По сравнению с применением t-распределения, использование z-оценки позволит построить не только более узкий доверительный интервал, но и получить более надежные оценки математического ожидания и среднеквадратического (стандартного) отклонения (σ), поскольку Z-оценка основывается на нормальном распределении.
Формула
Для определения граничных точек доверительного интервала, при условии что известно среднеквадратическое отклонение генеральной совокупности данных, используется следующая формула
где X – математическое ожидание выборки, α – уровень статистической значимости, Zα/2 – Z-оценка для уровня статистической значимости α/2, σ – среднеквадратическое отклонение генеральной совокупности, n – количество наблюдений в выборке. При этом, σ/√ n является стандартной ошибкой.
Таким образом, доверительный интервал для уровня статистической значимости α можно записать в виде
Пример
Предположим, что размер выборки насчитывает 25 наблюдений, математическое ожидание выборки равняется 15, а среднеквадратическое отклонение генеральной совокупности составляет 8. Для уровня значимости α=5% Z-оценка равна Zα/2=1,96. В этом случае нижняя и верхняя граница доверительного интервала составят
А сам доверительный интервал может быть записан в виде
Таким образом, мы можем утверждать, что с вероятностью 95% математическое ожидание генеральной совокупности попадет в диапазон от 11,864 до 18,136.
Методы сужения доверительного интервала
Допустим, что диапазон [11,864; 18,136] является слишком широким для целей нашего исследования. Уменьшить диапазон доверительного интервала можно двумя способами.
Снизив уровень статистической значимости до α=10%, мы получим Z-оценку равную Zα/2=1,64. В этом случае нижняя и верхняя граница интервала составят
А сам доверительный интервал может быть записан в виде
В этом случае, мы можем сделать предположение, что с вероятностью 90% математическое ожидание генеральной совокупности попадет в диапазон [12,376; 17,624].
Если мы хотим не снижать уровень статистической значимости α, то единственной альтернативой остается увеличение объема выборки. Увеличив ее до 144 наблюдений, получим следующие значения доверительных пределов
Сам доверительный интервал станет иметь следующий вид
Таким образом, сужение доверительного интервала без снижения уровня статистической значимости возможно только лишь за счет увеличения объема выборки. Если увеличение объема выборки не представляется возможным, то сужение доверительного интервала может достигаться исключительно за счет снижения уровня статистической значимости.
Построение доверительного интервала при распределении отличном от нормального
В случае если среднеквадратичное отклонение генеральной совокупности не известно или распределение отлично от нормального, для построения доверительного интервала используется t-распределение. Это методика является более консервативной, что выражается в более широких доверительных интервалах, по сравнению с методикой, базирующейся на Z-оценке.
Формула
Для расчета нижнего и верхнего предела доверительного интервала на основании t-распределения применяются следующие формулы
где X – математическое ожидание выборки, α – уровень статистической значимости, tα – t-критерий Стьюдента для уровня статистической значимости α и количества степеней свободы (n-1), σ – среднеквадратическое отклонение выборки, n – количество наблюдений в выборке.
Сам доверительный интервал может быть записан в следующем виде
Распределение Стьюдента или t-распределение зависит только от одного параметра – количества степеней свободы, которое равно количеству индивидуальных значений признака (количество наблюдений в выборке). Значение t-критерия Стьюдента для заданного количества степеней свободы (n) и уровня статистической значимости α можно узнать из справочных таблиц.
Пример
Предположим, что размер выборки составляет 25 индивидуальных значений, математическое ожидание выборки равно 50, а среднеквадратическое отклонение выборки равно 28. Необходимо построить доверительный интервал для уровня статистической значимости α=5%.
В нашем случае количество степеней свободы равно 24 (25-1), следовательно соответствующее табличное значение t-критерия Стьюдента для уровня статистической значимости α=5% составляет 2,064. Следовательно, нижняя и верхняя граница доверительного интервала составят
А сам интервал может быть записан в виде
Таким образом, мы можем утверждать, что с вероятностью 95% математическое ожидание генеральной совокупности окажется в диапазоне [38,442; 61,558].
Использование t-распределения позволяет сузить доверительный интервал либо за счет снижения статистической значимости, либо за счет увеличения размера выборки.
Снизив статистическую значимость с 95% до 90% в условиях нашего примера мы получим соответствующее табличное значение t-критерия Стьюдента 1,711.
В этом случае мы можем утверждать, что с вероятностью 90% математическое ожидание генеральной совокупности окажется в диапазоне [40,418; 59,582].
Если мы не хотим снижать статистическую значимость, то единственной альтернативой будет увеличение объема выборки. Допустим, что он составляет 64 индивидуальных наблюдения, а не 25 как в первоначальном условии примера. Табличное значение t-критерия Стьюдента для 63 степеней свободы (64-1) и уровня статистической значимости α=5% составляет 1,998.
Это дает нам возможность утверждать, что с вероятностью 95% математическое ожидание генеральной совокупности окажется в диапазоне [43,007; 56,993].
Выборки большого объема
К выборкам большого объема относятся выборки из генеральной совокупности данных, количество индивидуальных наблюдений в которых превышает 100. Статистические исследования показали, что выборки большего объема имеют тенденцию быть нормально распределенными, даже если распределение генеральной совокупности отличается от нормального. Кроме того, для таких выборок применение z-оценки и t-распределения дают примерно одинаковые результаты при построении доверительных интервалов. Таким образом, для выборок большого объема допускается применение z-оценки для нормального распределения вместо t-распределения.
Подведем итоги
В таблице собраны рекомендации по выбору методики построения доверительных интервалов для различных ситуаций.
ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ
Смотреть что такое «ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ» в других словарях:
Доверительный интервал — термин, используемый в математической статистике при интервальной (в отличие от точечной) оценке статистических параметров, что предпочтительнее при небольшом объёме выборки. Доверительным называют интервал, который покрывает неизвестный параметр … Википедия
Доверительный интервал — интервал, вычисленный по выборочным данным, который с заданной вероятностью (доверительной) накрывает неизвестное истинное значение оцениваемого параметра распределения. Источник: ГОСТ 20522 96: Грунты. Методы статистической обработки результатов … Словарь-справочник терминов нормативно-технической документации
доверительный интервал — для скалярного параметра генеральной совокупности – это отрезок, с большой вероятностью содержащий этот параметр. Эта фраза без дальнейших уточнений бессмысленна. Поскольку границы доверительного интервала оцениваются по выборке, естественна его… … Словарь социологической статистики
ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ — (confidence interval) Интервал, в котором достоверность значения параметра по населению, полученного на основе выборочного обследования, имеет определенную степень вероятности, например 95%, что обусловлено самой выборкой (sample). Ширина… … Экономический словарь
доверительный интервал — – интервал, в котором находится истинное значение определяемой величины с заданной доверительной вероятностью. Общая химия : учебник / А. В. Жолнин [1] … Химические термины
Доверительный интервал ДИ — Доверительный интервал, ДИ * давяральны інтэрвал, ДІ * confidence interval интервал значения признака, рассчитанный для к. л. параметра распределения (напр., среднего значения признака) по выборке и с определенной вероятностью (напр., 95% для 95% … Генетика. Энциклопедический словарь
доверительный интервал — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN confidence interval … Справочник технического переводчика
доверительный интервал — pasikliovimo intervalas statusas T sritis Standartizacija ir metrologija apibrėžtis Dydžio verčių intervalas, kuriame su pasirinktąja tikimybe yra matavimo rezultato vertė. atitikmenys: angl. confidence interval vok. Vertrauensbereich, m rus.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
доверительный интервал — pasikliovimo intervalas statusas T sritis chemija apibrėžtis Dydžio verčių intervalas, kuriame su pasirinktąja tikimybe yra matavimo rezultatų vertė. atitikmenys: angl. confidence interval rus. доверительная область; доверительный интервал … Chemijos terminų aiškinamasis žodynas
Доверительная вероятность и доверительный интервал.
Вероятность того, что истинное значение измеряемой величины лежит внутри некоторого интервала, называется доверительной вероятностью, или коэффициентом надежности,а сам интервал — доверительным интервалом.
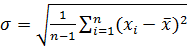
на так называемый коэффициент Стьюдента. Коэффициенты Стьюдента 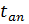
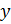
| Число измерений n | Доверительная вероятность y | ||
| 0,67 | 0,90 | 0,95 | 0,99 |
| 2,0 | 6,3 | 12,7 | 63,7 |
| 1,3 | 2,4 | 3,2 | 5,8 |
| 1,2 | 2,1 | 2,8 | 4,6 |
| 1,2 | 2,0 | 2,6 | 4,0 |
| 1,1 | 1,8 | 2,3 | 3,3 |
| 1,0 | 1,7 | 2,0 | 2,6 |
Окончательно, для измеряемой величины y при заданной доверительной вероятности y и числе измерений n получается условие
Величину 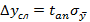
Пример: см. лекцию №5 – ряд чисел.
При числе измерений – 45 и доверительной вероятности – 0,95 получим, что коэффициент Стьюдента приблизительно равен 2,15. Тогда доверительный интервал для данного ряда измерений равен 62,6.
Источником грубых погрешностей нередко бывают резкие изменения условий измерения и ошибки, допущенные оператором:
— неправильный отсчет по шкале измерительного прибора, происходящий из-за неверного учета цены малых делений шкалы;
— неправильная запись результата наблюдений, значений отдельных мер использованного набора, например, гирь;
— хаотические изменения параметров напряжения, питающего средства измерения, например, его амплитуды или частоты.
Доверительный интервал за 15 минут
Добрый день, уважаемые читатели!
Меня зовут Кирилл Мильчаков. Сегодня мы продолжаем наш разговор о биостатистике. Тема сегодняшней нашей беседы будет «Доверительный интервал». Что такое доверительный интервал? Вы наверняка встречались с ним в научной литературе. Доверительный интервал 95 %, либо сочетание символов ДИ и CI (confidence interval) 95 %. Что же означают эти 95 %? Какие он еще может принимать значения? И как его рассчитывать самостоятельно? Об этом обо всем сегодня мы и поговорим в этой статье.
Видео-версия статьи о доверительном интервале
Генеральная совокупность и выборочная совокупность
Прежде чем углубляться в тайны доверительного интервала, хотел бы вспомнить с вами 2 основных понятия статистической совокупности, с которыми чаще всего работают – это генеральная совокупность или выборочная совокупность или выборка.
Генеральная совокупность – это тот массив данных, о которых вы хотите сделать выводы.
Выборка является частью генеральной совокупности, которая участвует непосредственно в вашем эксперименте. Есть такое понятие как репрезентативность, сегодня мы не будем его касаться, главное запомнить, что выборка должна быть репрезентативной.
Если привести небольшой пример относительно генеральной совокупности и выборки, то можно вспомнить о простом случае из вашей жизни. Когда вы хотите узнать, достаточно ли посолен суп, вы берете ложку супа и пробуете его. Вам необязательно есть весь суп, чтобы понять, насколько он посолен. Ложка в данном случае является выборкой, по которой вы делаете вывод обо всей кастрюле супа. В данном случае кастрюля супа является генеральной совокупностью, а ложка супа является выборкой.
Итак, мы вспомнили с вами о 2 ключевых статистических совокупностях – о генеральной совокупности и выборочной совокупности. Теперь нужно вспомнить, что типы исследования, которые проводятся над генеральной совокупностью и выборочной совокупностью, называют по-разному. Над генеральной совокупностью проводятся так называемые сплошные исследования, над выборочной совокупностью – выборочные.
Теперь вспомним небольшие отличия между параметрами этих 2 совокупностей. Сегодня для того, чтобы понять, что такое доверительный интервал, нам понадобятся следующие вещи: во-первых, отличие средней арифметической в генеральной совокупности и в выборочной совокупности. В генеральной совокупности она имеет значок µ (мю), в выборочной – это x̅ (х с чертой) — это средние арифметические по каждому виду совокупности.
Далее нужно знать, что стандартное отклонение имеет значок выборочной – либо S, либо SD (standard deviation), а в случае генеральной совокупности оно носит название среднеквадратичного отклонения и обозначается буквой σ (сигма).
Приведем пример расчета доврительного интервала
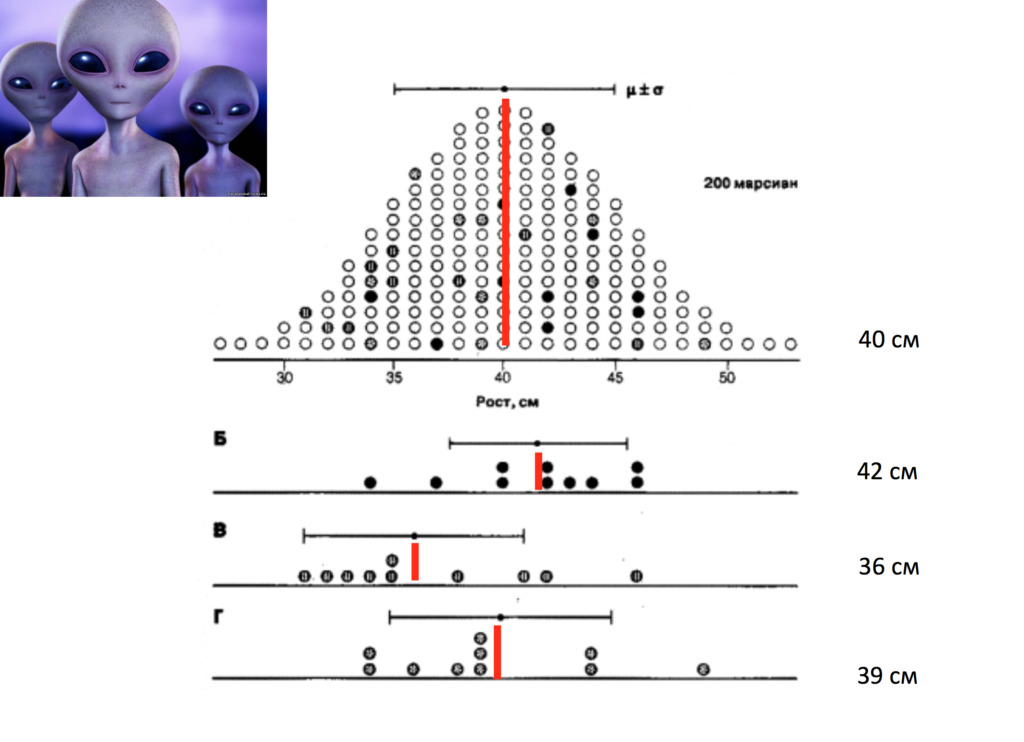
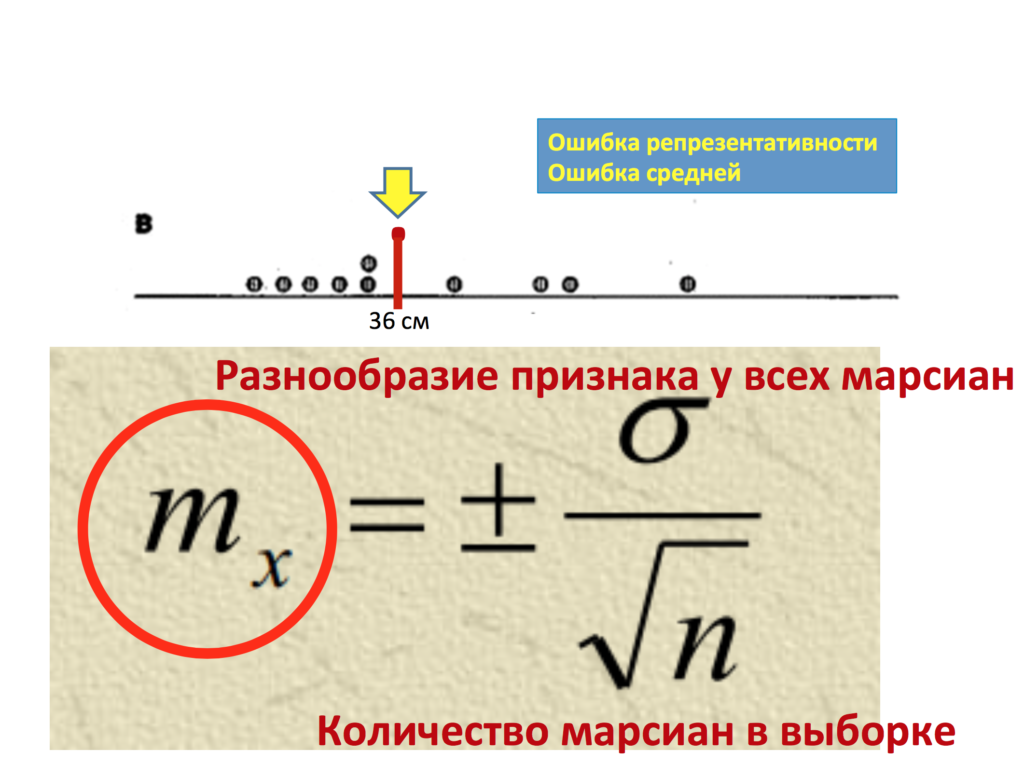
Представьте чисто гипотетическую ситуацию, когда перед нами стоит задача исследований среднего роста марсианина. Для того, чтобы его узнать, было отправлено 3 экспедиции. Первой из них повезло больше всего: они смогли поймать каждого из 200 марсианин и померить его рост.
Как мы помним, по закону нормального распределения по оси Х находится величина изучаемого признака, либо варианта (в данном случае это рост в сантиметрах), а по оси Y – частота встречаемости какого-то признака (мы его обозначаем буквой П.
Итак, оказалось, что у всех 200 марсиан средний рост составил 40 сантиметров. Таким образом, первая экспедиция смогла провести так называемое сплошное исследование, так как поработала со всеми единицами наблюдения генеральной совокупности. Поэтому мы имеем право назвать этот параметр µ.
Однако, второй и третьей экспедиции повезло гораздо меньше. Они попали в самые плохо населенные участки Марса и смогли отобрать только 10 марсиан. В данном случае оказалось, что средний рост по их выборке составил всего 38 сантиметров в первом случае и 41 сантиметр во втором случае.
Что же делать? Да, у нас есть данные из самого полного исследования, которое относится к первой экспедиции. Но представьте, что ни одна бы из них не смогла бы поработать со всей совокупностью полностью, и у нас были бы данные только от второй и третьей экспедиции. Что же в этой ситуации делать? Видно, что никто 40 сантиметров в действительности не достиг: во второй экспедиции Б она равна 38 сантиметрам, а в экспедиции В – 41 сантиметр. То есть в реальности никто не достиг 40 сантиметров. Что же делать в данном случае?
И вот здесь на помощь к нам приходит доверительный интервал, точнее оценка параметра. Доверительный интервал является вторым этапом оценки параметра. Прежде чем строить доверительный интервал, нам нужно понять, насколько в принципе этот параметр наша средняя (x̅б, x̅в) может отличаться, ошибаться от реального параметра в генеральной совокупности. Насколько?
Итак, предположим, мы нашли нашу ошибку репрезентативности mr. В данном случае она составила 2,7 сантиметра. Но что же это нам дает? А дает нам это уже достаточно много. Теперь мы, зная, насколько в принципе наша выборка может ошибаться относительно генеральной совокупности, можем составить определенное предположение о том, где же находится реальный параметр – реальные 40 сантиметров генеральной совокупности на основании данных лишь нашей выборки.
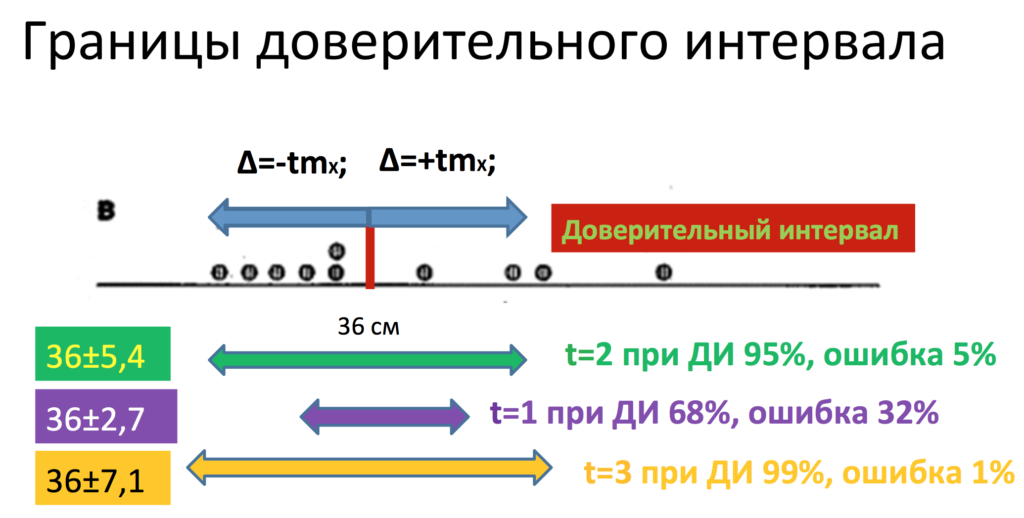
Для того, чтобы не залезать в критерий Стьюдента сегодня, я скажу лишь, что:
для доверительного интервала 95 % используется t=2,
для доверительного интервала 99 % используется t=3
и для доверительного интервала 68 % используется t=1.
Итак, после того, как мы нашли нашу предельную ошибку, мы можем построить доверительный интервал. Но для этого нам нужно самим задать тот доверительный интервал, который для нас подходит больше всего. Чаще всего в медицине используется вероятность ошибки 5 %, то есть доверительный интервал 95 % или вероятность ошибки 5 % (р=0,05, р=5 %).
Что же значат эти 95 %? А значат они следующее, что с 95%-ной вероятностью в нашем интервале лежит реальное значение, и лишь в 5 % случаев мы ошибаемся. То есть в нашем конкретном случае наша ошибка репрезентативности составила 2,7 сантиметра. Предельная ошибка отсюда будет равна чему? Именно 5,4 сантиметра, то есть доверительный интервал, так как здесь и плюс, и минус, то есть нам нужно ошибку умножить на 2, составил 10,8 сантиметров. А именно наши 38 см±5,4 см. Ширина всего доверительного интервала составляет 10,8 см. Напомню, что он складывается из положительной и отрицательной предельных ошибок вокруг нашей выборочной средней.
Итак, говоря о доверительном интервале, нужно сделать ряд важных выводов.
Если это видео оказалось Вам полезным, оно хотя бы немного раскрыло тайны доверительного интервала, ставьте лайки, подписывайтесь на наши рассылки и в комментариях пишите, какие темы по биостатистике вам бы были интересны для следующих выпусков. На этом я с вами прощаюсь. Меня зовут Кирилл. Пока!