Что такое дробно рациональное выражение
Преобразование рациональных выражений: виды преобразований, примеры
Статья рассказывает о преобразовании рациональных выражений. Рассмотрим виды рациональных выражений, их преобразования, группировки, вынесения за скобки общего множителя. Научимся представлять дробные рациональные выражения в виде рациональных дробей.
Определение и примеры рациональных выражений
Выражения, которые составлены из чисел, переменных, скобок, степеней с действиями сложения, вычитания, умножения, деления с наличием черты дроби, называют рациональными выражениями.
То есть это такие выражения, которые не имеют деления на выражения с переменными. Изучение рациональных выражений начинается с 8 класса, где их называют дробными рациональными выражениями. Особое внимание уделяют дробям в числителе, которые преобразовывают с помощью правил преобразования.
Это позволяет переходить к преобразованию рациональных дробей произвольного вида. Такое выражение может быть рассмотрено как выражение с наличием рациональных дробей и целых выражений со знаками действий.
Основные виды преобразований рациональных выражений
Рациональные выражения используются для того, чтобы выполнять тождественные преобразования, группировки, приведение подобных, выполнение других действий с числами. Цель таких выражений – это упрощение.
Преобразуем в числителе формулу разности квадратов, тогда получаем, что
Представление в виде рациональной дроби
Алгебраическая дробь чаще всего подвергается упрощению при решении. Каждое рациональное приводится к этому разными способами. Необходимо выполнить все необходимые действия с многочленами для того, чтобы рациональное выражение в итоге смогло дать рациональную дробь.
Следует начать с умножения, тогда получим, что
Производим представление полученного результата с исходное. Получим, что
Теперь выполняем вычитание:
После деления придем к рациональной дроби вида
Можно решить это иначе.
Что такое дробно рациональное выражение
В курсе алгебры 7 класса мы занимались преобразованиями целых выражений, т. е. выражений, составленных из чисел и переменных с помощью действий сложения, вычитания и умножения, а также деления на число, отличное от нуля. Так, целыми являются выражения
В отличие от них выражения
помимо действий сложения, вычитания и умножения, содержат деление на выражение с переменными. Такие выражения называют дробными выражениями.
Целые и дробные выражения называют рациональными выражениями.
Целое выражение имеет смысл при любых значениях входящих в него переменных, так как для нахождения значения целого выражения нужно выполнить действия, которые всегда возможны.
Дробное выражение при некоторых значениях переменных может не иметь смысла. Например, выражение не имеет смысла
при а = 0. При всех остальных значениях а это выражение имеет
смысл. Выражение имеет смысл при тех значениях х и у, x ≠ y.
Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных.
Выражение вида называется, как известно, дробью.
Дробь, числитель и знаменатель которой многочлены, называют рациональной дробью.
Примерами рациональных дробей служат дроби
В рациональной дроби допустимыми являются те значения переменных, при которых не обращается в нуль знаменатель дроби.
Пример 1. Найдем допустимые значения переменной в дроби
Это уравнение имеет два корня: 0 и 9. Следовательно, допустимыми значениями переменной а являются все числа, кроме 0 и 9.
Дробь равна нулю тогда и только тогда, когда a = 0 и b ≠ 0.
2. Основное свойство дроби. Сокращение дробей
Мы знаем, что для обыкновенных дробей выполняется следующее свойство: если числитель и знаменатель дроби умножить на одно и то же натуральное число, то значение дроби не изменится. Иначе говоря, при любых натуральных значениях а, b и с верно paвенство
Докажем, что это равенство верно не только при натуральных, но и при любых других значениях а, b и с, при которых знаменатель отличен от нуля, т. е. при b ≠ О и с ≠ О.
Пусть Тогда по определению частного а = bm. Умножим обе части этого равенства на с :
На основании сочетательного и переместительного свойств умножения имеем:
Так как bс ≠ 0, то по определению частного
Мы показали, что для любых числовых значений переменных b и с, где b ≠ О и с ≠ 0, верно равенство
Равенство (1) сохраняет силу и в том случае, когда под буквами а, b и с понимают многочлены, причем b и с — ненулевые многочлены, т. е. многочлены, не равные тождественно нулю.
Равенство (1) выражает основное свойство рациональной дроби:
если числитель и знаменатель рациональной дроби умножить на один и тот же ненулевой многочлен, то получится равная ей дробь.
Это равенство верно при всех допустимых значениях переменных. Такие равенства будем называть тождествами. Ранее тождествами мы называли равенства, верные при всех значениях переменных. Теперь мы расширяем понятие тождества.
Определение. Тождеством называется равенство, верное при всех допустимых значениях входящих в него переменных.
Основное свойство рациональной дроби позволяет выполнять приведение дроби к новому знаменателю и сокращение дробей. Приведем примеры.
Пример 1. Приведем дробь к знаменателю
Множитель называют дополнительным множителем к числителю и знаменателю дроби
Пример 2. Приведем дробь к знаменателю
Для этого числитель и знаменатель данной дроби умножим на -1:
если изменить знак числителя (или знак знаменателя) дроби и знак перед дробью, то получим выражение, тождественно равное данному.
Пример 3. Сократим дробь
Разложим числитель и знаменатель дроби на множители:
Сократим полученную дробь на общий множитель a + 3:
Пример 4. Построим график функции
Графиком функции является прямая, а графиком функции но с «выколотой» точкой (4 ; 4) (рис. 1.)
Содержание:
Рациональные выражения
Деление степеней и одночленов
В курсе алгебры 7 класса вы ознакомились с целыми выражениями, научились складывать и вычитать их, умножать и возводить в степень. Теперь рассмотрим, как можно делить выражения. Разделить выражение A на выражение В —означает найти такое выражение X1 при котором X•В = А.
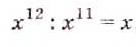
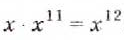
Следовательно, если а — отличное от нуля число, 

Ведь по правилу умножения степеней, 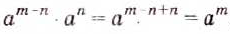
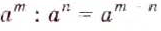
при делении степеней с одинаковыми основание оставляют без изменения, а из показателя степени делимого вычитают показатель а степени делителя.
Пользуясь этим правилом, можно записать:
Если 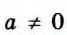
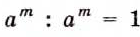
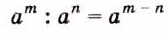
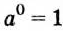
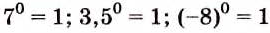
Рассмотрим, как можно делить одночлены.
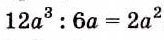
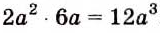
Чтобы разделить одночлен на одночлен, необходимо:
Пример:
Надо разделить одночлен 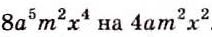
Решение:
Делим 8 на 4, 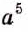
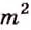
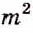
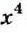
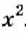
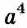
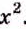
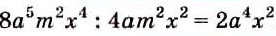
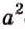
Хотите знать ещё больше?
Рассмотрим, как можно делить не только одночлены, но и выражения, содержащие степени многочленов. Например,
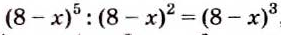
Иногда перед делением надо преобразовать многочлены. Разделим, например, 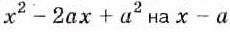
Известны и другие способы деления многочленов. В частности, многочлены можно делить «углом», подобно тому, как делят числа. Сравните, например, деление чисел 7488 и 234 и деление многочленов
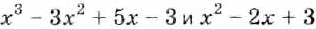

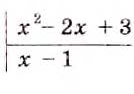
Частное от деления многочленов не всегда является многочленом, как и частное от деления двух целых чисел не всегда число целое. То есть во множестве многочленов деление не всегда возможно.
Выполним вместе!
Пример:
Решение:
а) 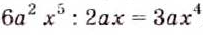
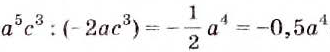
Ответ. а) 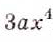
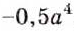
Пример:
Проверьте, правильно ли выполнено деление: 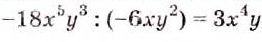
Решение:
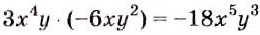
Произведение частного и делителя тождественно равно делимому, следовательно, деление выполнено верно.
Пример:
Упростите выражение: 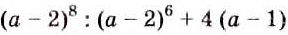
Решение:
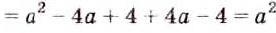
Ответ:
Деление и дроби
Деление двух целых выражений не всегда можно выполнить без остатка. Например, частные 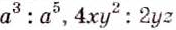
Если частное от деления одного выражения на другое не является целым выражением, то его записывают в виде дроби. Например:
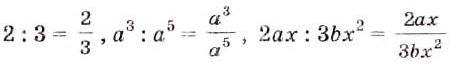
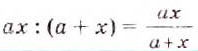
Дробью называют частное от деления двух выражений, записанное с помощью черты дроби.
Подобно другим выражениям дроби бывают числовые и содержащие переменные.
Например, дроби 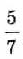
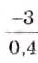
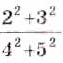
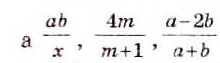
выражения, содержащие переменные.
Запись 
при а = 5 не имеет смысла. При всех других значениях а она имеет смысл. Говорят, что для данной дроби допустимы все значения переменной а, кроме а = 5.
Для переменных, входящих в знаменатель дроби, допустимы только те значения, которые не превращают этот знаменатель в нуль.
Рассмотрим две дроби:
Два выражения, соответствующие значения которых равны при всех допустимых значениях переменных, называются тождественно равными, или тождественными.
Это определение отличается от аналогичного определения для целых выражений только словом «допустимых». Говоря только о целых выражениях, это слово ранее мы исключали, поскольку для них все значения переменных допустимы.
Два тождественных выражения, соединённых знаком равенства, образуют тождество. Замена одного выражения другим, тождественным ему, называется тождественным преобразованием данного выражения.
Хотите знать ещё больше?
Примеры обыкновенных дробей:
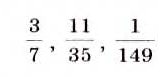
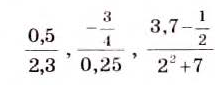
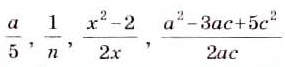
Общее понятие дроби довольно широкое. Кроме алгебраических бывают неалгебраические дроби, вам ещё неизвестные, например.
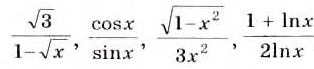
Пример:
Какие значения переменных допустимы для дроби: а) 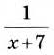
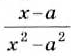
Решение:
6) допустимы все значения, кроме х =а и х = -а.
Пример:
Докажите, что дробь 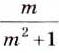
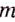
При каждом рациональном значении 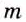
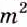
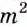
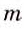
Следовательно, при каждом значении 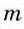
Пример:
Тождественны ли выражения:
а) 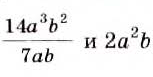
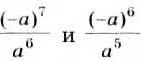
Решение:
а) Представим дробь 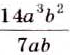
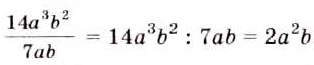
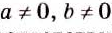
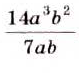
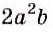
б) Выполним действия в каждом выражении, используя свойства степеней: 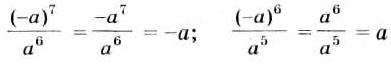
При всех допустимых значениях переменных (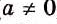
Ответ. а) Выражения тождественны; 6) выражения нетождественны.
Основное свойство дроби
Вспомните основное свойство обыкновенной дроби. Если числитель и знаменатель обыкновенной дроби умножить на одно и то же натуральное число, то получим равную ему дробь. Иными словами, при любых натуральных a, b и
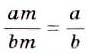
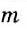
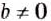
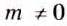
Пусть 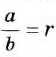
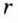
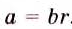
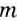
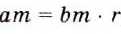
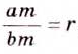
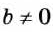
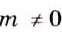
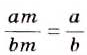
Доказанное тождество справедливо для любых дробей и является основным свойством дроби.
Если числитель и знаменатель дроби умножить или разделить на одно и то же выражение, то получим дробь, которая тождественно равна данной.
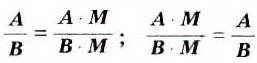
Здесь под «выражением» понимают выражение с переменными, которое тождественно не равно нулю, либо число, отличное от нуля.
Основное свойство дроби даёт возможность заменить дробь вида
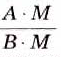
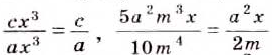
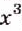
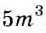
Исходя из основного свойства дроби, приходим к следующим выводам.
Если члены дроби — многочлены, то перед сокращением дроби их часто необходимо разложить на множители. Иногда перед сокращением дроби изменяют знак числителя или знаменателя, изменив соответственно и знак перед дробью.
Примеры:
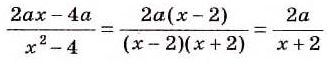
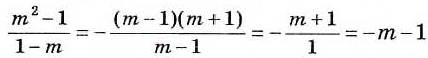
Примечание. Последнее преобразование и равенство 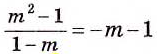
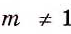
Сократить дробь можно делением числителя и знаменателя на их общий делитель, выраженный не только целым выражением, но и дробным. Например, можно записать
Это равенство — тождество, верное при условии 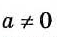
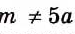
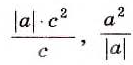
Такие дроби не относятся к алгебраическим дробям. Подробнее с ними вы ознакомитесь в старших классах. А теперь рассмотрим наиболее простые случаи. Первую дробь можно сократить на с. Равенство 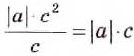
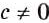
Решение:
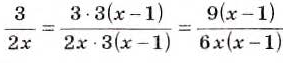
Ответ. а) 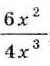
Пример:
Приведите к общему знаменателю дроби 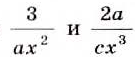
Решение:
Общий знаменатель — 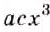
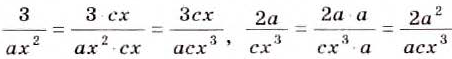
Ответ. 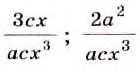
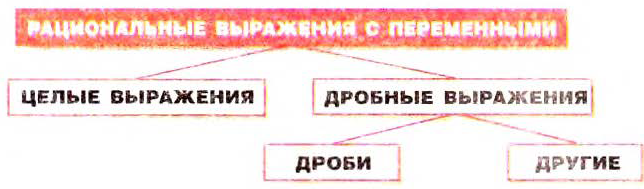
Рациональные выражения
Выражение, составленное из чисел и переменных с помощью действий сложения, вычитания, умножения, деления или возведения в степень, называется рациональным.
Примеры рациональных выражений:
Целые выражения — это рациональные выражения, не содержащие действия деления на переменную.
Дробные выражения это рациональные выражения, содержащие действие деления на переменную.
Целые выражения и дроби — простейшие виды рациональных выражений. Другие виды этих выражений связаны между собой, как показано на схеме (рис. 9).
Словом «другие» здесь обозначены дробные рапиональные выражения, которые не являются дробями, например:
Уравнение называется рациональным, если его левая и правая части — рациональные выражения.
Рациональное уравнение называется дробным, если его правая или левая части — выражения дробные.
Примеры дробных уравнений:
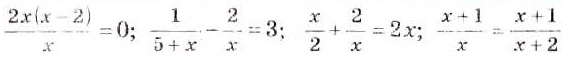
Для того чтобы решать такие уравнения, необходимо знать, как выполняют действия с дробными выражениями. Поэтому в следующих параграфах будем рассматривать сложение, вычитание, умножение, деление и возведение дробей в степень.
Простейшие дробные уравнения, то есть уравнения, в которых левая часть — это дробь, а правая — нуль, решают пользуясь условием равенства дроби нулю.
Дробь равна нулю тогда и только тогда, когда числитель равен нулю, а знаменатель отличный от нуля.
Например, чтобы решить уравнение 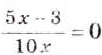
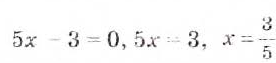
Кроме того, проверить, не равен ли нулю при таком значении х знаменатель:
Следовательно, 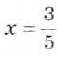
Обратите внимание! Условие равенства дроби нулю состоит из двух частей:
Каждая из этих частей условия является одинаково важной.
Хотите знать ещё больше!
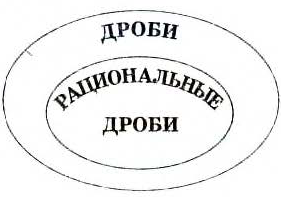
В представленной выше схеме словом «дроби» называют только рациональные дроби (часть рациональных выражений). Но дроби бывают не только рациональные, например,
Это также дроби, но нерациональные. Поэтому, забегая немного вперёд, соотношение между разными видами выражений можно представить в виде диаграммы (рис. 10).
Если выражение содержит переменные под знаком модуля, его не считают рациональным При этом многие такие выражения можно заменить двумя, тремя либо большим количеством рациональных выражений. Например, рассмотрим дробь 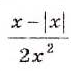
Если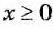
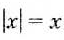
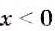
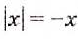
Пример:
При каких значениях переменной х значение дроби 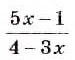
Решение:
Пример:
Имеет ли корни уравнение 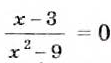
Решение:
Ответ. Уравнение корней не имеет.
Сложение и вычитание дробей
Для натуральных чисел а, b, с справедливо равенство
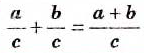
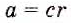
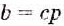
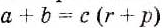
По определению действия деления, из полученного равенства следует, что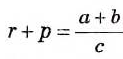
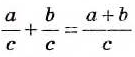
Аналогично можно доказать и тождество
Из этих двух тождеств следуют правила сложения и вычитания дробей с одинаковыми знаменателями.
Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тот же.
Чтобы найти разность дробей с одинаковыми знаменателями, необходимо из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить тот же.
На основании этих правил выполняют сложение и вычитание любых дробей с одинаковыми знаменателями:
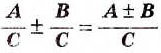
Примеры:
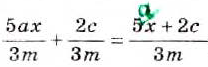
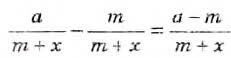
Чтобы найти сумму или разность дробей с разными знаменателями, сначала их нужно привести к общему знаменателю, как при сложении и вычитании обыкновенных дробей.
Чтобы привести дроби к общему знаменателю, знаменатель каждой дроби нужно разложить на множители. Если знаменатели дробей не имеют общих множителей, то сложение и вычитание выполняют по формуле:
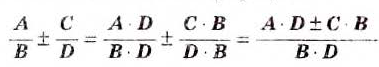
Примеры:
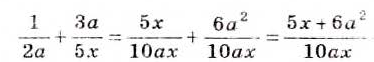
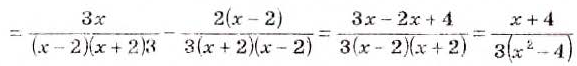
Иногда нужно найти сумму или разность дроби и целого выражения. Их можно складывать или вычитать, как дроби, записав целое выражение в виде дроби со знаменателем 1.
Пример:
Аналогично упрощают выражения, состоящие из трёх или более дробей, соединённых знаками плюс» или «минус». Например,
Хотите знать ещё больше?
Если рассматривать каждое тождество только при его допустимых значениях переменных, то ость при условии, что левая и правая части имеют смысл, то мы сознательно упрощаем задачу. Доказательство, подтверждаем лишь то. что оно верно на всей области допустимых значений, но не указываем, какая это область.
Чтобы получить исчерпывающее решение такой задачи, необходимс не только убедиться, что тождество правильное для всей области допустимых значений, но и показать, какова эта область. Либо чётко указать, какие из действительных чисел не относятся к этой области. Например, показав, что 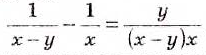
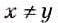
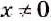
Выполним вместе!
Пример:
Найдите разность дробей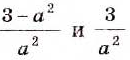
Решение:
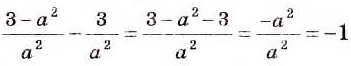
Пример:
Найдите сумму дробей 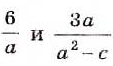
Решение:
Общий знаменатель дробей а(а 2 — с). Чтобы привести данные дроби к общему знаменателю, надо умножить первую дробь на а 2 — с, а вторую — на а.
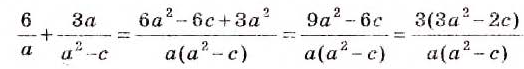
Ответ. 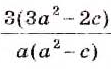
Пример:
Выполните действия: 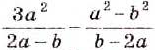
Решение:
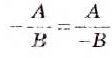
Умножение дробей
Правило умножения обыкновенных дробей вы уже знаете. Для любых натуральных чисел а, b, с и d справедливо равенство
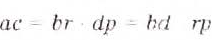
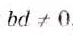
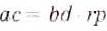
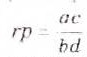
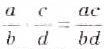
Чтобы умножить дробь на дробь, нужно перемножить их числители и отдельно — знаменатели, затем первое произведение записать числителем, а второе — знаменателем дроби.
На основании этого правила выполняют умножение любых дробей:
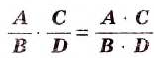
Примеры:
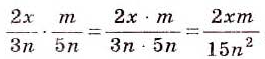
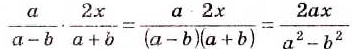
Поскольку целое выражение можно считать дробью со знаменателем 1, то, по сформулированному правилу, можно перемножать дроби и целые выражения.
Примеры:
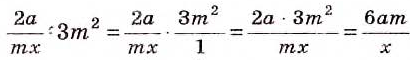
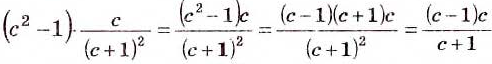
Правило умножения дробей распространяется на произведение трёх множителей и более, например:
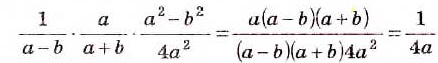
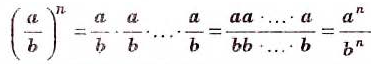
Чтобы возвести дробь в степень, необходимо возвести в эту степень числитель и знаменатель, затем первый результат записать в числителе, а второй — в знаменателе дроби. 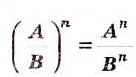
Пример:
Возведём дробь 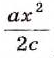
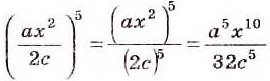
Хотите знать ещё больше?
Вы уже знаете, что для умножения многочленов возможно обратное преобразование: разложение многочленов на множители. Существует ли преобразование, обратное умножению дробей?
Любую дробь можно представить как произведение двух, трёх или произвольного количества других дробей, Например,
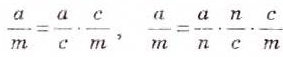
Преобразование, обратное умножению дробей, неоднозначно, неопределенно. Упростим задачу. Представьте дробь 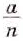
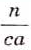
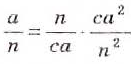
Решение таких задач в более сложных случаях, как и операций, обратных возведению дробей в степень, рассмотрим позднее.
Выполним вместе!
Пример:
Найдите произведение добей: 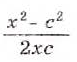
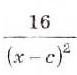
Решение:
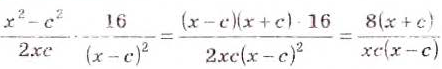
Ответ.
Пример:
Найдите значение выражения 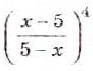
Решение:
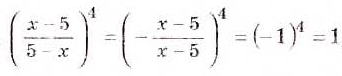
Ответ. При каждом значении х, кроме х= 5, значение данного выражения равно 1.
Пример:
Представьте в виде степени дроби выражение 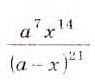
Решение:
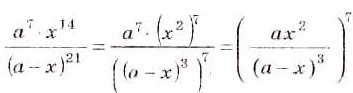
Ответ. 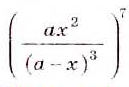
Деление дробей
Действие деления дробей — обратное умножению:
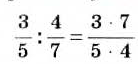
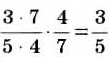
Аналогично 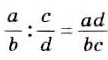
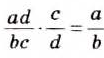
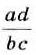
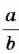
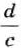
Дробь 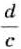
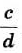
Чтобы разделить две дроби, нужно первую дробь умножить на дробь, обратную второй.
Примеры:
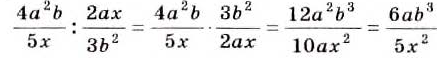
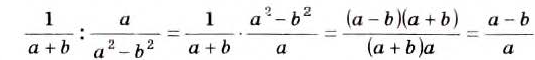
Поскольку целое выражение можно представить в виде дроби со знаменателем 1, то, согласно сформулированному правилу, дробь можно делить на целое выражение и целое выражение — на дробь:
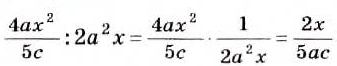
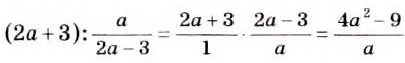
Хотите знать ещё больше?
Проанализируем, при каких значениях переменных а, b, с, d значение частного 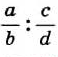
Знаменатели дробей не равны нулю, поэтому 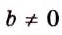
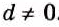
Следовательно, данное частное имеет значение только в том случае, если выполняются все три следующих условия: 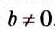
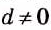
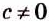
Рассмотрим, при каких значениях х имеет смысл выражение 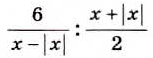
Если 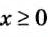
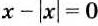
Если 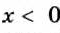
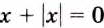
Выполним вместе!
Пример:
Упростите выражение 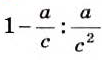
Решение:
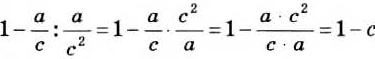
Пример:
Найдите частное от деления дроби 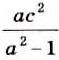
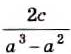
Решение:
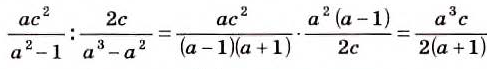
Вторая дробь не имеет смысла, если а 2 (а-1)=0, то есть при а = 0 или а = 1.
При с = 0 значение второй дроби равно 0, а на нуль делить нельзя.
Следовательно, частное этих дробей существует, если 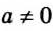
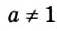
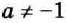
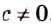
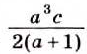
Преобразование рациональных выражений
Вы уже знаете, что любое числовое выражение после выполнения всех действий принимает конкретное значение, выраженное некоторым числом. Преобразования рациональных выражений выполняют так же, как находят значение числового выражения. Заданное выражение заменяют другим, тождественным ему. Такие преобразования называются тождественными преобразованиями.
Тождественные преобразования рациональных выражений выполняют частями или «цепочкой», используя известные вам из предыдущих параграфов правила действий с дробями и целыми выражениями. Если выражение содержит несколько действий разных ступеней, то их выполняют в такой же последовательности, что и преобразования числовых выражений:
Любое рациональное дробное выражение можно представить в виде дроби, а некоторые — даже в виде целого выражения. Рассмотрим, например, выражения:
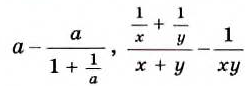
Первое из них можно преобразовать таким образом:
1) 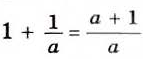
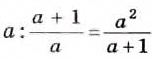
3) 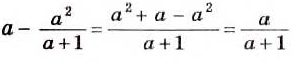
Следовательно, 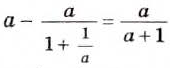
Аналогичным способом (последовательно) можно упростить и второе выражение. А можно преобразовать и «цепочкой»:
Хотите знать больше?
В математике часто приходится не только упрощать выражения, например сумму нескольких дробей записать одним выражением, но и осуществлять обратные операции.
Задача (О. Коши):
Решение. Пусть 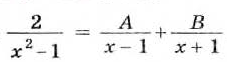
Преобразуем правую часть равенства в дробь:
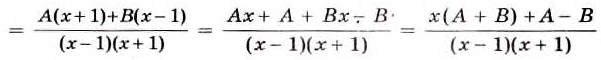
Подставляем это выражение в правую часть (1):
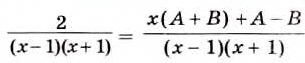
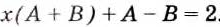
Следовательно, 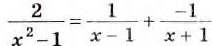
Ответ. 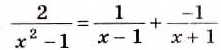
Рациональные уравнения
Умение преобразовывать дробные выражения необходимо, в частности, для решения дробных уравнений.
Вы уже знаете, что уравнение ‚ называется рациональным, если его левая и правая части — рациональные выражения. Рациональное уравнение называют дробным, если его правая, левая либо правая и левая части — дробные выражения.
Примеры дробных уравнений:
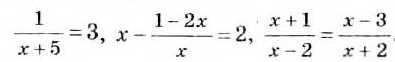
При решении целого уравнения его часто стараются заменить равносильным. С дробными уравнениями это возможно лишь в некоторых случаях. Их преимущественно заменяют уравнениями-следствиями.
Уравнения называют следствием данного, если все решения данного уравнения удовлетворяют полученное уравнение.
Уравнение-следствие удовлетворяют все корни данного уравнения, но кроме них оно может иметь и посторонние корни.
Дробные рациональные уравнения можно решать разными способами. В частности:
Рассмотрим на конкретных примерах каждый способ.
Пример:
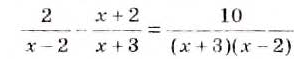
Решение:
Заменим данное уравнение равносильным, в котором правая часть — нуль, а левая — дробь. Для этого дробь перенесём из правой части в левую, изменив знак перед ней на противоположный, и упростим полученное дробное выражение:
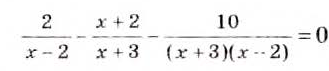
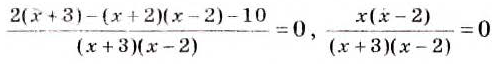
Полученное уравнение равносильно данному. Решить его просто, поскольку дробь равна нулю лишь тогда, когда числитель равен нулю, а знаменатель отличный от нуля.
Приравняем числитель к нулю: 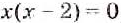
Следовательно, х = 2 не удовлетворяет данное уравнение.
Пример:
Решение:
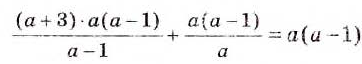
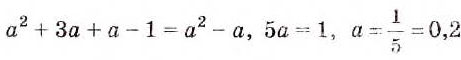
Проверка. 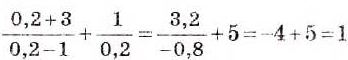
Если дробное уравнение имеет вид пропорции либо его можно представить в виде пропорции, то используется основное свойство пропорции. В этом случае также получаем уравнение-следствие.
Известные вам линейные уравнения — это отдельный вид рациональных уравнений. Как именно связаны между собой рациональные уравнения, иллюстрирует рисунок 18. Рациональные уравнения, которые не являются целыми, называют дробно-рациональными. Только некоторые из них сводятся к линейным. Большая часть дробнорациональных уравнений сводится к таким, решать которые вы ещё не умеете. Решение некоторых из них рассмотрим позднее.

Дробно-рациональными бывают не только уравнения с одной, но и с двумя, тремя и большим количеством переменных, а также системы таких уравнений. Например, решим систему уравнений:
Суммируем левые и правые части этих уравнений и получим:
Подставляем это значение х в первое уравнение: 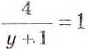
Выполним вместе!
Пример:
Решите уравнение 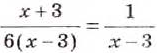
Решение:
Ответ. Уравнение решений не имеет.
Пример:
Какое число нужно прибавить к членам дроби 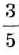

Решение:
Обозначим искомое число буквой х. Тогда по условию задачи:
Поверка. 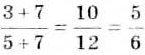
Ответ. Искомое число равно 7.
Степени с целыми показателями
Некоторые дроби часто записывают в виде степеней с отрицательными показателями. Например, вместо
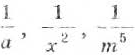
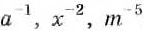
Вспомните, как делят степени с одинаковыми основаниями:
Рассматривая степени только с положительными показателями, отмечают, что последнее равенство верно только при 
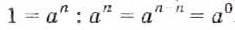
Поэтому условились, что 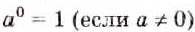
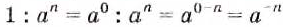
Следовательно, желательно условиться, что
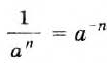
Итак, можно рассматривать степени с произвольными целыми показателями. Объясним кратко смысл этого понятия:
Свойства степеней с целыми показателями такие же, как и степеней с натуральными показателями:
Докажем первое из этих тождеств (его называют основным свойством степеней) для случая, когда 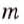
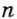

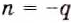
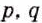
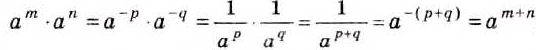
Аналогично можно доказать равенство 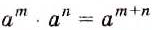
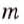
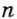
Обратите внимание на степени, в которых основание или показатель равны нулю.
Если а и n не равны нулю, то
Выражение 0° не имеет смысла, это не число, как и выражение 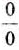
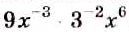
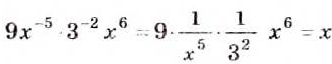
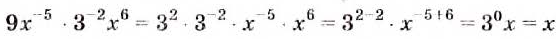
Выполним вместе!
Пример:
Решение:
а) 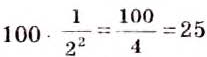
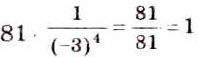
Пример:
Запишите без знаменателя выражение 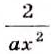
Решение:
Ответ. 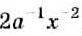
Пример:
Упростите выражение: 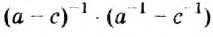
Решение:
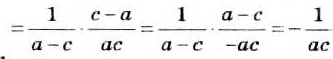
Ответ: 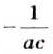
Стандартный вид числа
Как выполнять действия с числами, записанными в стандартном виде, покажем на примерах.
Обратите внимание!
Числа, записанные в стандартном виде, выражают преимущественно приближённые значения величин. Это объясняется тем, что так часто записывают значения расстояний, площадей, масс, объёмов, скоростей, температур, которые почти всегда приближённые.
Хотите знать ещё больше?
Как следует понимать выражение число х больше, чем у, на порядок? Это означает, что число х больше у приблизительно в 10 раз.
Выполним вместе! Пример:
Запишите в стандартном виде число: а) 320; б) 0,4; в) 1000 000; г) 0,00000027.
Решение:
Пример:
Решение:
Функция y=k/x
Функция
Вспомните, что такое аргумент функции, её область определения, множество значении, как задают функции
Далее мы рассмотрим функцию, заданную формулой 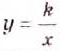
Например, дана функция 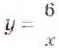
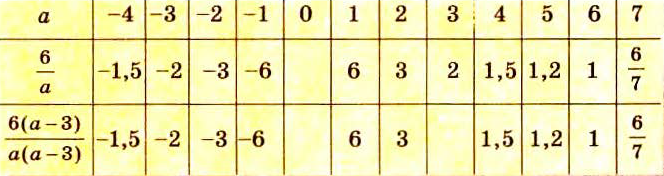
| х | -6 | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| y | -1 | -1.2 | -1.5 | -2 | -3 | -6 | — | 6 | 3 | 2 | 1.5 | 1.2 | 1 |
Обозначим точки, координаты которых приведены в таблице (рис. 23, а). Если бы на этой же координатной плоскости было нанесено больше точек, координаты которых удовлетворяют равенство 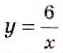
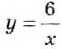
График функции 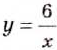
Если таким способом построить график функции 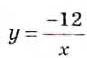
График каждой функции 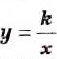
Степени с целыми показателями вводили в математику постепенно. Около 4 тыс. лет тому назад учёные Вавилона рассматривали квадрат и куб числа при вычислении площади квадрата и объёма куба. Донаших дней сохранились глиняные плитки с таблицами квадратов и кубов натуральных чисел, изготовленные древними вавилонянами. Со временем учёные стали рассматривать четвёртую, пятую степени и выше, называя их сначала квадрато-квадратом, кубо-квадратом и т. д.
Степень с нулевым показателем ввели в V в. независимо друг от друга самаркандец ал-Каши и француз Ф. Н. Шюке. Степени с отрицательными показателями Ф. Н. Шюке также использовал. Теорию степеней с отрицательными показателями разработал в ХVII в. английский математик Д. Валлис. Он отождествлял последовательности
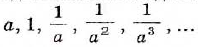
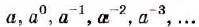
Стандартный вид числа ввели в науку только в ХХ в. с началом использования электронных вычислительных машин (ЭВМ).
ОСНОВНОЕ В ГЛАВЕ
Частное от деления выражения А на выражение В можно записать в виде дроби 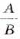
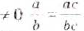
Действия с любыми дробями можно выполнять так же, как с обыкновенными дробями. Если знаменатели не равны нулю, то всегда
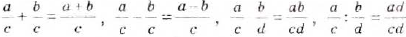
Свойства степеней с целыми показателями аналогичны свойствам степеней с натуральными показателями. Если числа m и n — целые, а и b — отличные от нуля, то всегда:
Функция 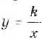
Функция у = х 2
| х | -3 | -2,5 | -2 | -1,5 | -1 | 0 | 1 | 1,5 | 2 | 2,5 | 3 |
| y | 9 | 6,25 | 4 | 2,25 | 1 | 0 | 1 | 2,25 | 4 | 6,25 | 9 |
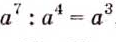
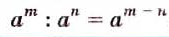
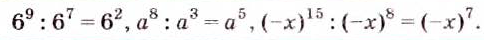
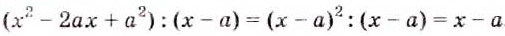
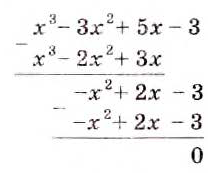
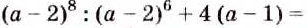
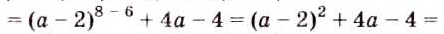
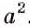
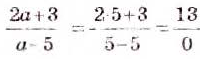
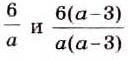
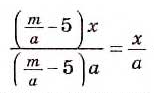
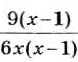
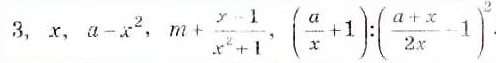
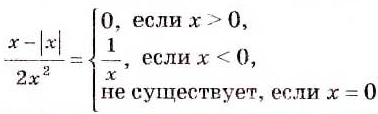
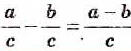
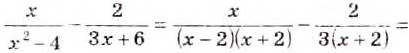
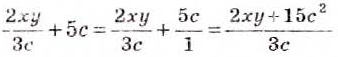
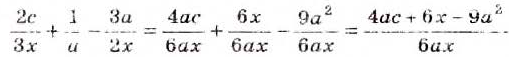
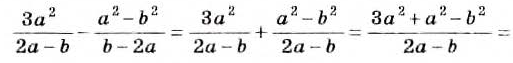
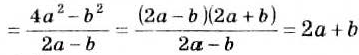
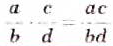
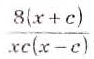
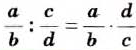
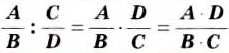
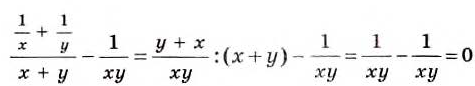
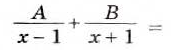
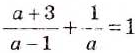
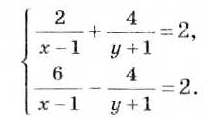
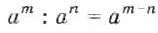
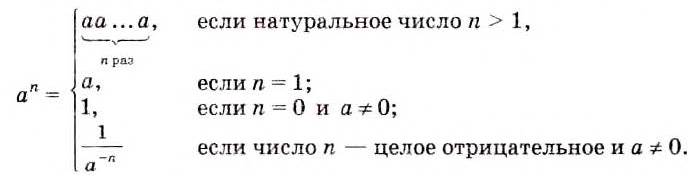
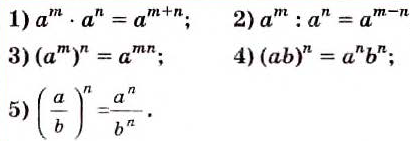
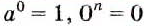
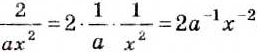
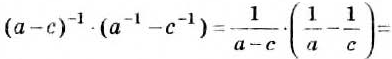
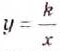
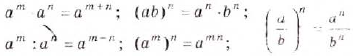
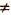 0
0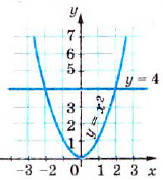
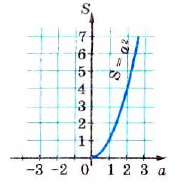 Рис. 36
Рис. 36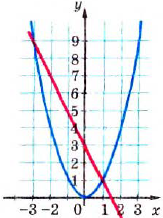 Рис. 37
Рис. 37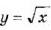
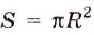 , где R — радиус круга,
, где R — радиус круга, 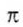 = 3,14. Отсюда
= 3,14. Отсюда 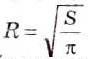 . Путь, пройденный телом при свободном падении, определяем по формуле
. Путь, пройденный телом при свободном падении, определяем по формуле 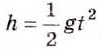 , где t — время, g — постоянное число. Отсюда
, где t — время, g — постоянное число. Отсюда 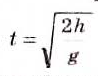 Рассмотрим свойства функции
Рассмотрим свойства функции 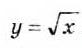 .
.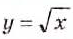 (рис. 49,б). Этот график — одна ветвь параболы. Она выходит из начала координат и располагается в первом координатном углу. Функция
(рис. 49,б). Этот график — одна ветвь параболы. Она выходит из начала координат и располагается в первом координатном углу. Функция 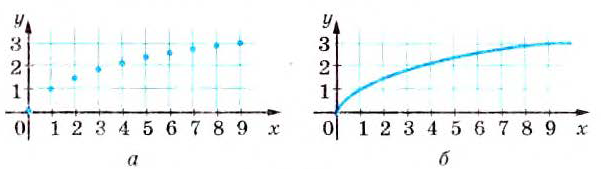 Рис. 49
Рис. 49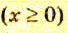
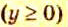
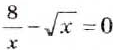 .
.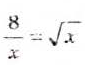 и построим в одной системе координат графики функций
и построим в одной системе координат графики функций 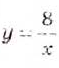 и
и 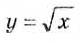 (рис. 50)
(рис. 50)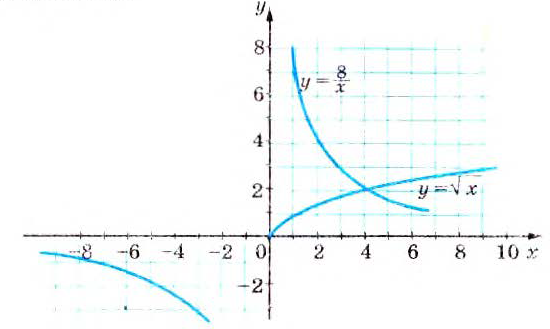 Рис. 50
Рис. 50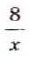 и
и 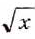 принимают равные значения, то есть число 4 — корень (возможно, приближённый) уравнения
принимают равные значения, то есть число 4 — корень (возможно, приближённый) уравнения 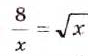 . Подставляем х = 4 в данное уравнение и убеждаемся, что 4 точный корень. Построенные графики других общих точек не имеют, следовательно, данное уравнение имеет только один корень: х = 4.
. Подставляем х = 4 в данное уравнение и убеждаемся, что 4 точный корень. Построенные графики других общих точек не имеют, следовательно, данное уравнение имеет только один корень: х = 4.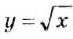 не обязательно строить по точкам. Этот график для х > О симметричен графику функции у = x 2 относительно биссектрисы первого координатного угла. Ведь равенства
не обязательно строить по точкам. Этот график для х > О симметричен графику функции у = x 2 относительно биссектрисы первого координатного угла. Ведь равенства 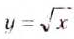 и
и 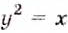 при положительном х выражают одну и ту же зависимость между переменными х и у. Если во втором из этих равенств поменять х на у, а у на х, то это равнозначно замене оси х осью у и наоборот. Такие функции, как
при положительном х выражают одну и ту же зависимость между переменными х и у. Если во втором из этих равенств поменять х на у, а у на х, то это равнозначно замене оси х осью у и наоборот. Такие функции, как 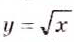 и
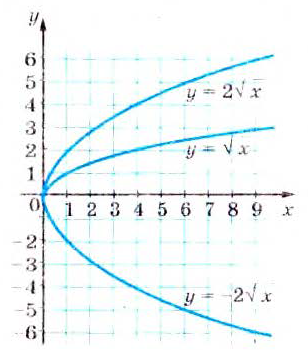
и 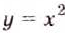 называются обратными. Постройте их графики в одной системе координат и убедитесь, что они симметричны относительно прямой у = х.
называются обратными. Постройте их графики в одной системе координат и убедитесь, что они симметричны относительно прямой у = х.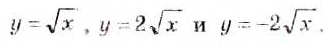
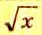
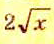
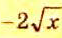
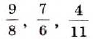 виде десятичных дробей. Для этого их числители разделим на знаменатели. Итак,
виде десятичных дробей. Для этого их числители разделим на знаменатели. Итак, 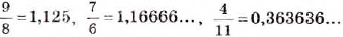 В двух последних примерах деление можно продолжать бесконечно (почему?). Полученные доли частного — это бесконечные десятичные дроби, цифры которых периодически повторяются. Это бесконечные периодические десятичные дроби.
В двух последних примерах деление можно продолжать бесконечно (почему?). Полученные доли частного — это бесконечные десятичные дроби, цифры которых периодически повторяются. Это бесконечные периодические десятичные дроби. ,
,  ,
, 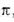 , получаем бесконечные непериодические десятичные дроби:
, получаем бесконечные непериодические десятичные дроби: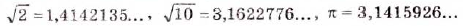
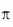 и
и 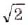 с точностью до тысячных, пишут:
с точностью до тысячных, пишут: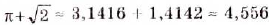
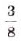 : б)
: б) 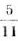 ; в)
; в) 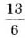 .
.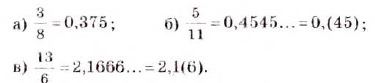
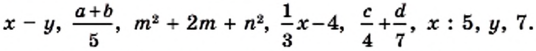
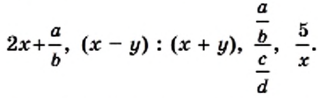
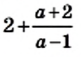 при
при 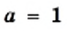 не имеет смысла, то есть числового значения этого выражения при
не имеет смысла, то есть числового значения этого выражения при 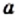 это выражение имеет смысл.
это выражение имеет смысл.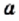 являются все числа, кроме 1.
являются все числа, кроме 1. . Так, рациональные выражения
. Так, рациональные выражения 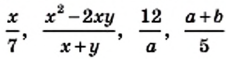 являются примерами рациональных дробей.
являются примерами рациональных дробей.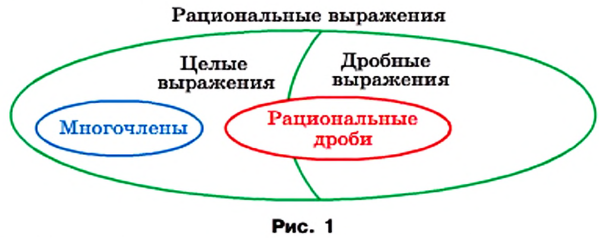
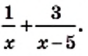
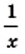 имеет смысл при всех значениях
имеет смысл при всех значениях 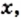 кроме
кроме 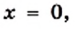 а дробь
а дробь 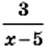 имеет смысл при всех значениях
имеет смысл при всех значениях 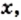 кроме
кроме 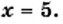
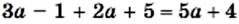 является тождеством, так как оно выполняется при любых значениях
является тождеством, так как оно выполняется при любых значениях 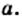
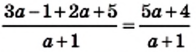 также естественно считать тождеством. Но оно выполняется не при любых значениях
также естественно считать тождеством. Но оно выполняется не при любых значениях 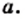 При
При 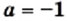 рациональные дроби, входящие в данное равенство, не имеют смысла.
рациональные дроби, входящие в данное равенство, не имеют смысла.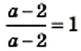 является тождеством, поскольку оно выполняется при всех допустимых значениях
является тождеством, поскольку оно выполняется при всех допустимых значениях 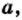 то есть при всех
то есть при всех 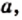 кроме
кроме 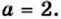
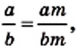
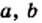 и
и 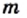 — некоторые числа, причем
— некоторые числа, причем 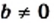 и
и 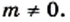
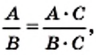
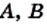 и
и 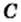 — многочлены, причем многочлены
— многочлены, причем многочлены 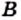 и
и 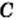 ненулевые.
ненулевые.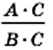 можно заменить на тождественно равную ему дробь
можно заменить на тождественно равную ему дробь 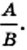 Такое тождественное преобразование называют сокращением дроби на множитель
Такое тождественное преобразование называют сокращением дроби на множитель 
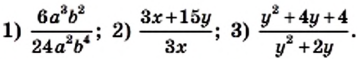
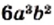 и
и 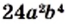 имеют общий множитель
имеют общий множитель 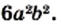 Тогда
Тогда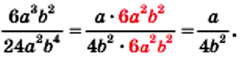
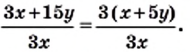
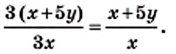
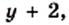 получаем:
получаем: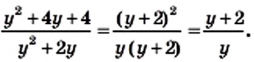
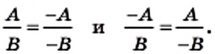
 и можно записать в виде выражения
и можно записать в виде выражения 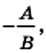
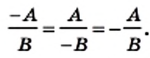
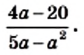
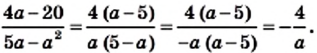
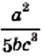 к знаменателю
к знаменателю 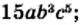
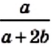 к знаменателю
к знаменателю 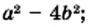
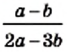 к знаменателю
к знаменателю 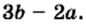
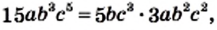 то новый знаменатель отличается от знаменателя данной дроби множителем
то новый знаменатель отличается от знаменателя данной дроби множителем 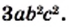 Следовательно, числитель и знаменатель данной дроби надо умножить на дополнительный множитель
Следовательно, числитель и знаменатель данной дроби надо умножить на дополнительный множитель  Имеем:
Имеем: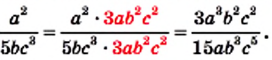
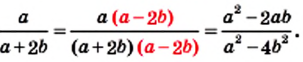
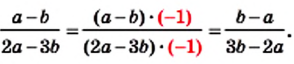
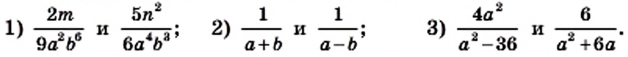
 Однако удобнее в качестве общего знаменателя взять одночлен
Однако удобнее в качестве общего знаменателя взять одночлен 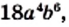 сконструированный таким образом: его коэффициент 18 является наименьшим общим кратным коэффициентов 9 и 6 знаменателей данных дробей, а каждая из переменных
сконструированный таким образом: его коэффициент 18 является наименьшим общим кратным коэффициентов 9 и 6 знаменателей данных дробей, а каждая из переменных 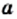 и
и 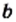 взята в степени с наибольшим показателем степени из тех, с которыми она входит в знаменатели данных дробей.
взята в степени с наибольшим показателем степени из тех, с которыми она входит в знаменатели данных дробей.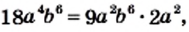 то дополнительным множителем для дроби
то дополнительным множителем для дроби 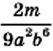 является одночлен
является одночлен 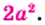 Учитывая, что
Учитывая, что 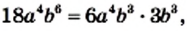 получаем, что дополнительным множителем для дроби
получаем, что дополнительным множителем для дроби 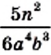 является одночлен
является одночлен 
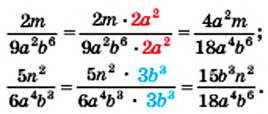
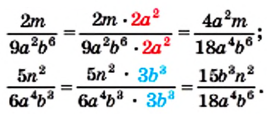
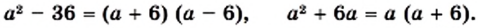
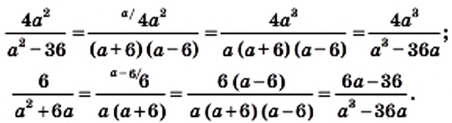
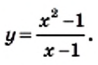
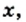 кроме 1. Имеем:
кроме 1. Имеем: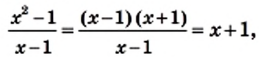
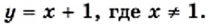
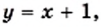 за исключением одной точки, абсцисса которой равна 1 (рис. 2).
за исключением одной точки, абсцисса которой равна 1 (рис. 2).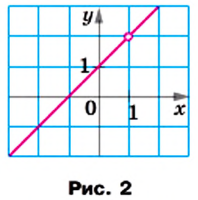
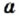 решите уравнение
решите уравнение 
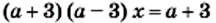 и рассмотрим три случая.
и рассмотрим три случая.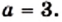
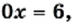 которое не имеет корней.
которое не имеет корней.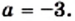
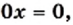 корнем которого является любое число.
корнем которого является любое число.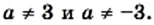
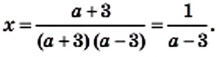
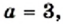 то уравнение не имеет корней; если
то уравнение не имеет корней; если 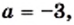 то корнем является любое число; если
то корнем является любое число; если 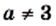 и
и 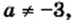 то
то 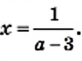
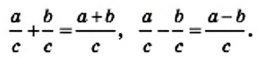
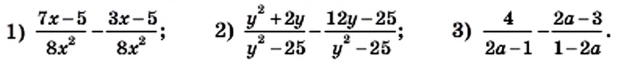
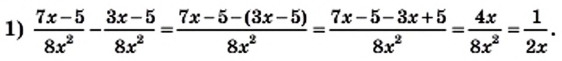
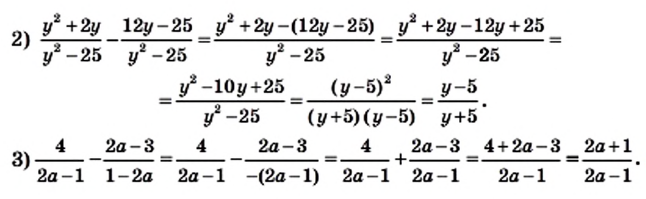
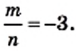 Найдите значение выражения
Найдите значение выражения 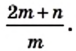
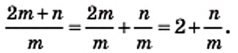
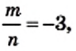 то
то 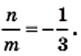 Следовательно,
Следовательно, 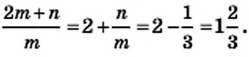
 при которых значение выражения
при которых значение выражения 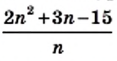 является целым числом.
является целым числом.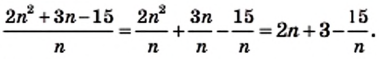
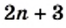 принимает натуральные значения при любом натуральном
принимает натуральные значения при любом натуральном 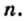 Поэтому выражение
Поэтому выражение 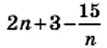 принимает целые значения, если значения выражения
принимает целые значения, если значения выражения 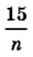 являются целыми числами. Это возможно только при следующих натуральных значениях
являются целыми числами. Это возможно только при следующих натуральных значениях 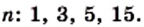
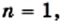 или
или 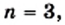 или
или 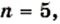 или
или 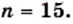
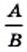 и
и 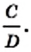
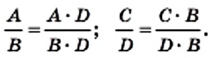
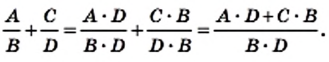

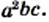
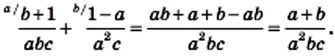
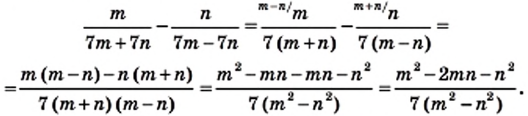
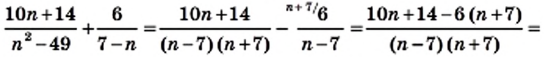
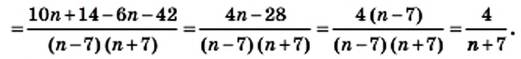
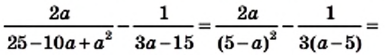
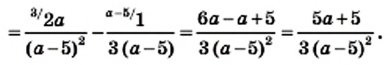
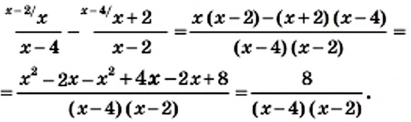
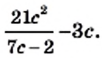
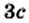 в виде дроби со знаменателем 1, получаем:
в виде дроби со знаменателем 1, получаем: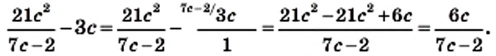
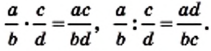
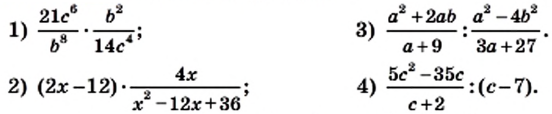
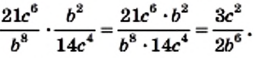
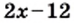 в виде дроби со знаменателем 1, получаем:
в виде дроби со знаменателем 1, получаем: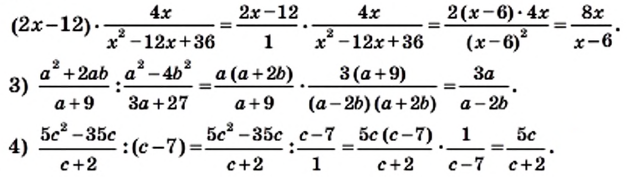
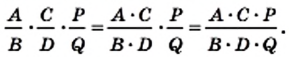
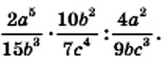
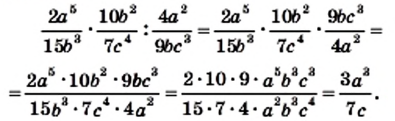
 имеем:
имеем:
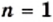 договорились, что
договорились, что 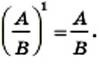
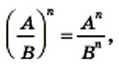
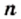 — натуральное число.
— натуральное число.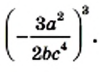
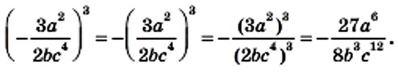
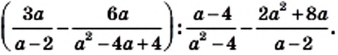
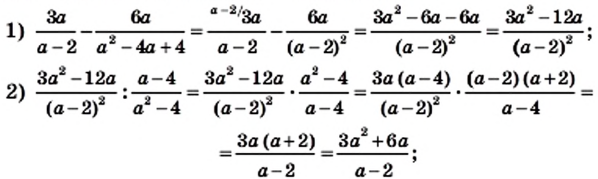
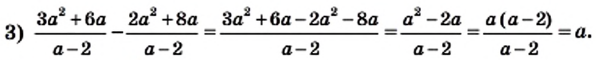
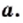
 не зависит от значения
не зависит от значения 
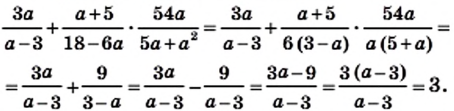
 значение данного выражения равно 3.
значение данного выражения равно 3.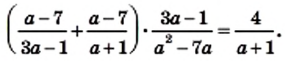
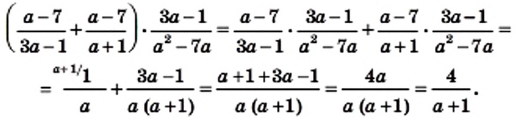
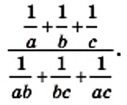
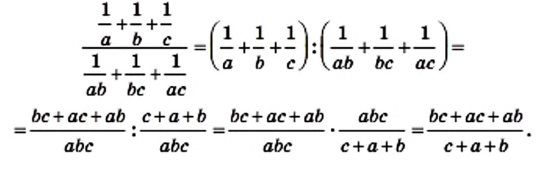
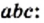
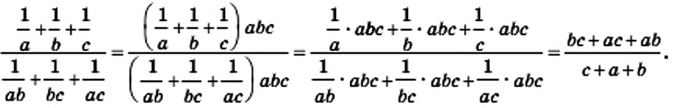
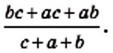
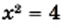 и
и 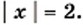 Очевидно, что каждое из них имеет одни и те же корни:
Очевидно, что каждое из них имеет одни и те же корни: 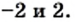 Говорят, что уравнения
Говорят, что уравнения 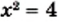 и
и 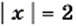 равносильны. Приведем еще примеры пар равносильных уравнений:
равносильны. Приведем еще примеры пар равносильных уравнений: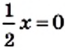 и
и 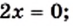
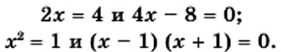
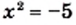 и
и 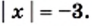 Каждое из этих уравнений не имеет корней. Такие уравнения также принято считать равносильными.
Каждое из этих уравнений не имеет корней. Такие уравнения также принято считать равносильными.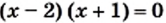 и
и 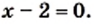 Однако эти уравнения не являются равносильными, так как первое уравнение имеет еще один корень, равный —1, который не является корнем второго уравнения.
Однако эти уравнения не являются равносильными, так как первое уравнение имеет еще один корень, равный —1, который не является корнем второго уравнения.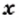 км/ч — искомая скорость. Тогда скорость автомобиля на второй части пути равна
км/ч — искомая скорость. Тогда скорость автомобиля на второй части пути равна 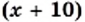 км/ч. Автомобиль преодолел первую часть пути за
км/ч. Автомобиль преодолел первую часть пути за 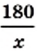 ч, а вторую — за
ч, а вторую — за 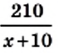 ч.
ч.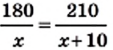 является математической моделью рассмотренной реальной ситуации. Обе части полученного уравнения являются рациональными выражениями.
является математической моделью рассмотренной реальной ситуации. Обе части полученного уравнения являются рациональными выражениями.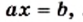 является рациональным.
является рациональным.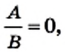 где
где 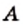 и
и 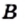 — многочлены.
— многочлены.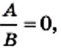 нужно потребовать одновременного выполнения двух условий:
нужно потребовать одновременного выполнения двух условий: 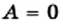 и
и 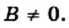 Это значит, что при решении уравнений указанного вида следует руководствоваться таким алгоритмом:
Это значит, что при решении уравнений указанного вида следует руководствоваться таким алгоритмом: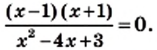
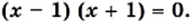 Корнями этого уравнения являются числа —1 и 1.
Корнями этого уравнения являются числа —1 и 1.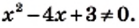 При
При 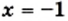 получаем, что
получаем, что 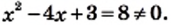 При
При 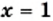 получаем, что
получаем, что 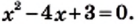
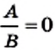 сводится к решению уравнения
сводится к решению уравнения 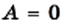 и проверке условия
и проверке условия 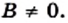
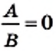 равносильно системе
равносильно системе 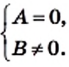
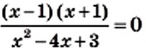 равносильно системе
равносильно системе 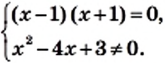
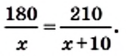
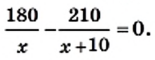
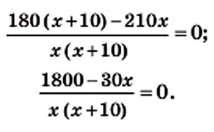
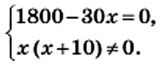
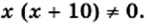
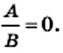 Именно так мы и поступили, решая уравнение
Именно так мы и поступили, решая уравнение 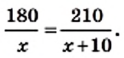
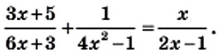
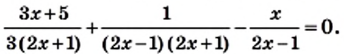 Представив левую часть этого уравнения в виде рациональной дроби, получим:
Представив левую часть этого уравнения в виде рациональной дроби, получим: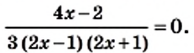
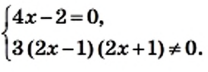
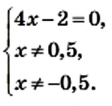
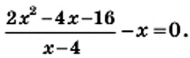
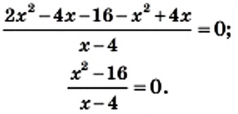
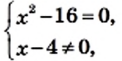
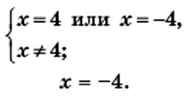
 км/ч. Тогда ее скорость по течению реки составляет
км/ч. Тогда ее скорость по течению реки составляет 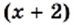 км/ч, а против течения
км/ч, а против течения 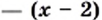 км/ч. Турист проплыл 3 км по течению за
км/ч. Турист проплыл 3 км по течению за 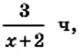 а 2 км против течения —
а 2 км против течения — 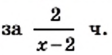 Поскольку весь путь был пройден за
Поскольку весь путь был пройден за 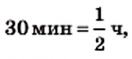 то
то 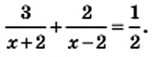
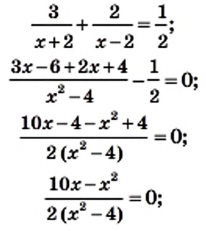
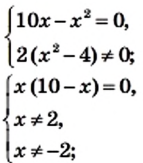
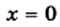 или
или 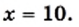
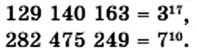
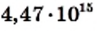 км. Масса Солнца равна 1 990 000 000 000 000 000 000 000 000 000 кг, или
км. Масса Солнца равна 1 990 000 000 000 000 000 000 000 000 000 кг, или 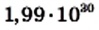 кг.
кг.
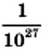 и
и 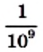 соответственно
соответственно 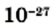 и
и 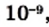 , то для рассмотренных величин получим «одноэтажную» форму записи:
, то для рассмотренных величин получим «одноэтажную» форму записи: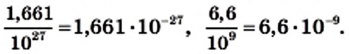
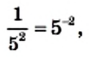
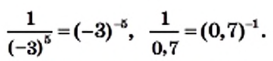
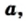 не равного нулю, и натурального числа
не равного нулю, и натурального числа 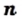
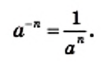
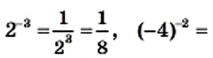
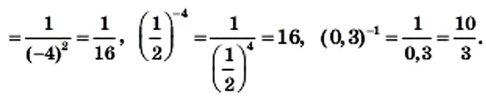
 не равного нулю,
не равного нулю, 
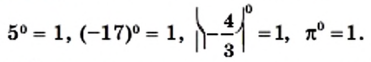
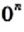 при целых
при целых 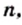 меньших или равных нулю, не имеет смысла.
меньших или равных нулю, не имеет смысла.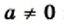 и делом
и делом 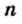 числа
числа 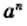 и
и 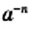 являются взаимно обратными. Поэтому равенство
являются взаимно обратными. Поэтому равенство 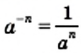 выполняется при любом целом
выполняется при любом целом 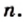
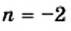 имеем:
имеем: 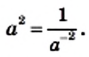
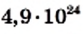 кг. Масса Марса равна
кг. Масса Марса равна 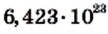 кг. Площадь поверхности Луны равна
кг. Площадь поверхности Луны равна 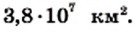 » Числа, выражающие эти величины, записаны в так называемом стандартном виде.
» Числа, выражающие эти величины, записаны в так называемом стандартном виде.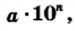 где
где 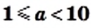 и
и 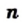 — целое число.
— целое число.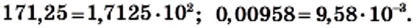 Однако на практике стандартный вид числа используют для записи больших и малых значений величин. При этом порядок числа дает представление о величине. Например, если порядок числа
Однако на практике стандартный вид числа используют для записи больших и малых значений величин. При этом порядок числа дает представление о величине. Например, если порядок числа 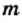 равен 3, то есть
равен 3, то есть 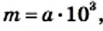 то с учетом того, что
то с учетом того, что 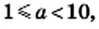 получаем:
получаем: 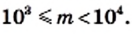
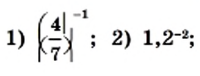
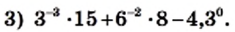
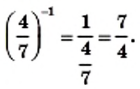
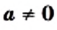 и
и 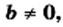 то
то 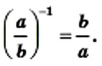
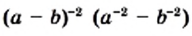 в виде рациональной дроби.
в виде рациональной дроби.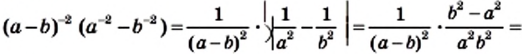
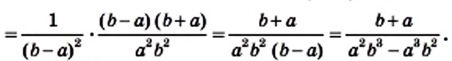
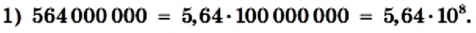
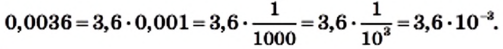
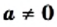 и любых целых
и любых целых 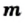 и
и 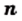 выполняются равенства:
выполняются равенства: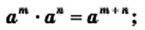 (1)
(1)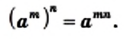 (2)
(2) и
и  любого целого
любого целого 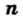 выполняется равенство
выполняется равенство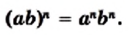 (3)
(3)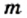 и
и 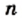 это равенство уже было доказано в курсе алгебры 7 класса.
это равенство уже было доказано в курсе алгебры 7 класса.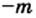 и
и 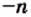 — натуральные числа. Тогда
— натуральные числа. Тогда 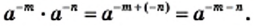
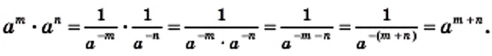
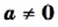 и любых целых
и любых целых 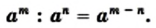 (4)
(4)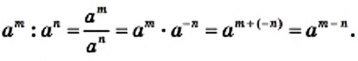
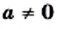 и
и 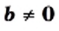 любого целого
любого целого 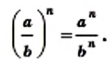 (5)
(5)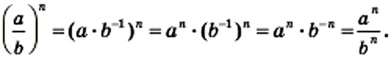
 выражение:
выражение: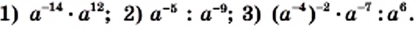
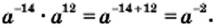
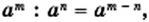 получаем:
получаем: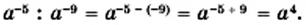
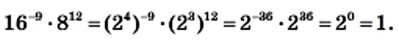
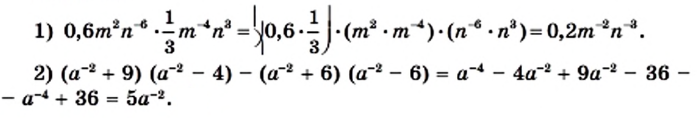
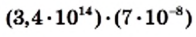 и результат запишите в стандартном виде.
и результат запишите в стандартном виде.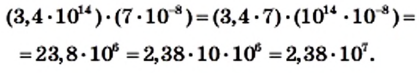
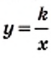 и ее график
и ее график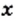 грн цену 1 кг товара, а через
грн цену 1 кг товара, а через 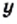 кг — количество этого товара, которое можно приобрести за 500 грн.
кг — количество этого товара, которое можно приобрести за 500 грн.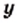 от переменной
от переменной 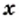 является обратной пропорциональностью: увеличение цены
является обратной пропорциональностью: увеличение цены 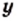 во столько же раз и, наоборот, уменьшение цены приводит к увеличению количества купленного товара.
во столько же раз и, наоборот, уменьшение цены приводит к увеличению количества купленного товара.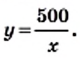
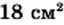 , а стороны —
, а стороны — 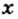 см и
см и 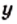 см. Тогда
см. Тогда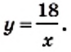
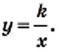
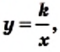 где
где 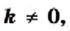 называют обратной пропорциональностью.
называют обратной пропорциональностью.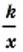 допустимыми значениями переменной
допустимыми значениями переменной 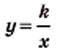 — также являются все числа, кроме 0.
— также являются все числа, кроме 0.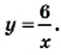 В таблице приведены некоторые значения аргумента и соответствующие им значения функции.
В таблице приведены некоторые значения аргумента и соответствующие им значения функции.
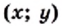 которых приведены в таблице (рис. 3).
которых приведены в таблице (рис. 3).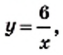 нам удастся отметить, тем меньше полученная фигура (рис. 4) будет отличаться от графика функции
нам удастся отметить, тем меньше полученная фигура (рис. 4) будет отличаться от графика функции 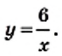
 не имеет общих точек с осью ординат.
не имеет общих точек с осью ординат.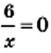 не имеет решений. Следовательно, число 0 не принадлежит области значений данной
не имеет решений. Следовательно, число 0 не принадлежит области значений данной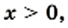 то
то 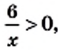 то есть
то есть 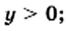 если
если 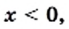 то
то 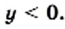 Следовательно, точки графика данной функции могут находиться только в I и III координатных четвертях.
Следовательно, точки графика данной функции могут находиться только в I и III координатных четвертях.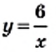 до оси абсцисс уменьшаются и могут стать сколь угодно малыми, но никогда не будут равны нулю. Действительно, чем больше модуль аргумента, тем меньше модуль соответствующего значения функции.
до оси абсцисс уменьшаются и могут стать сколь угодно малыми, но никогда не будут равны нулю. Действительно, чем больше модуль аргумента, тем меньше модуль соответствующего значения функции.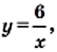 то мы получили бы фигуру, изображенную на рисунке 5.
то мы получили бы фигуру, изображенную на рисунке 5. 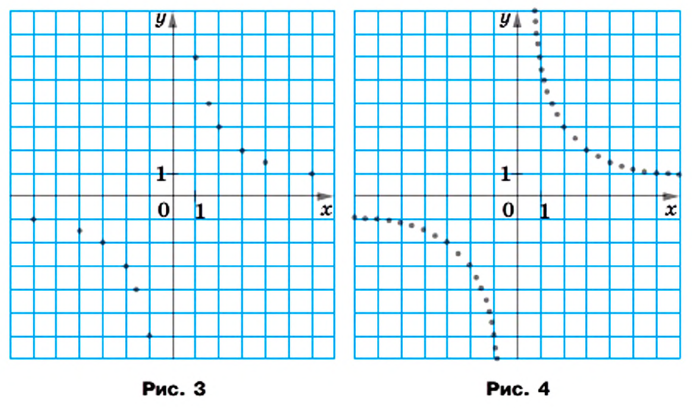
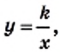 , где
, где  называют гиперболой. Гипербола состоит из двух частей — ветвей гиперболы.
называют гиперболой. Гипербола состоит из двух частей — ветвей гиперболы. то также верно равенство
то также верно равенство 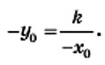 Тогда можно сделать следующий вывод: если точка
Тогда можно сделать следующий вывод: если точка 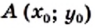 принадлежит гиперболе
принадлежит гиперболе 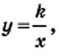 то точка
то точка 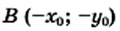 также принадлежит этой гиперболе.
также принадлежит этой гиперболе.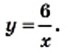
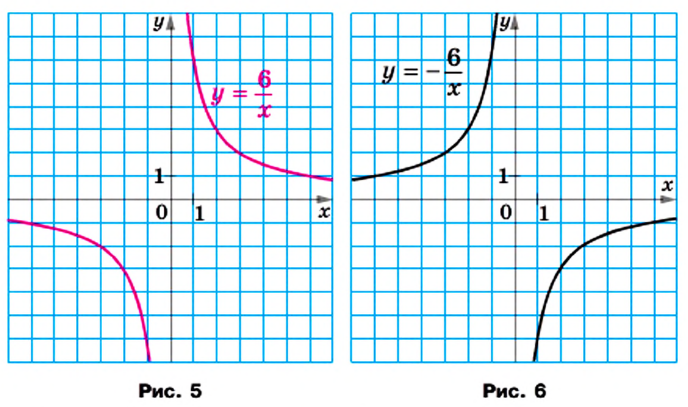
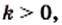 то ветви гиперболы расположены в I и III четвертях, а если
то ветви гиперболы расположены в I и III четвертях, а если  — то во II и IV четвертях.
— то во II и IV четвертях.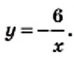 . Ветви гиперболы
. Ветви гиперболы 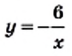 расположены во II и IV четвертях.
расположены во II и IV четвертях.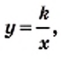 где
где 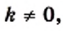 являются все числа, кроме 0.
являются все числа, кроме 0.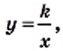 изученные в этом пункте.
изученные в этом пункте.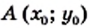 принадлежит гиперболе
принадлежит гиперболе 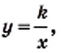 то точка
то точка 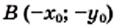 также принадлежит этой гиперболе.
также принадлежит этой гиперболе.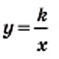 можно использовать при решении уравнений.
можно использовать при решении уравнений.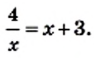
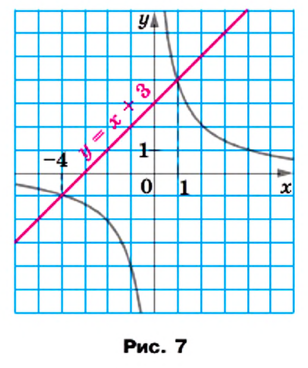
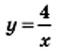 и
и 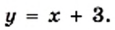 Построим в одной системе координат графики этих функций (рис. 7). Они пересекаются в двух точках, абсциссы которых равны 1 и —4. В каждой из точек пересечения графиков значение функции
Построим в одной системе координат графики этих функций (рис. 7). Они пересекаются в двух точках, абсциссы которых равны 1 и —4. В каждой из точек пересечения графиков значение функции 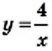 равно значению функции
равно значению функции 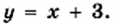 Следовательно, при найденных абсциссах значения выражении
Следовательно, при найденных абсциссах значения выражении 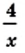 и
и 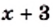 равны, то есть числа 1 и —4 являются корнями уравнения
равны, то есть числа 1 и —4 являются корнями уравнения 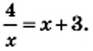 Проверка это подтверждает. Действительно,
Проверка это подтверждает. Действительно, 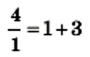 и
и 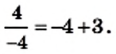
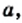 не равного нулю, и натурального числа
не равного нулю, и натурального числа 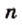
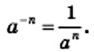
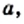 не равного нулю,
не равного нулю, 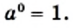
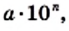 где
где 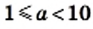 и
и 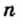 — целое число.
— целое число.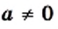 и
и 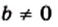 и любых целых
и любых целых 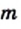 и
и 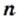 выполняются равенства:
выполняются равенства: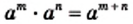 (основное свойство степени);
(основное свойство степени);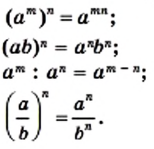
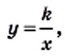 , где
, где 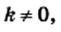 называют обратной пропорциональностью.
называют обратной пропорциональностью.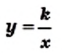
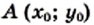 принадлежит гиперболе
принадлежит гиперболе 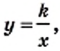 то точка
то точка 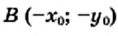 также принадлежит этой гиперболе.
также принадлежит этой гиперболе.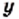 площадь квадрата со стороной
площадь квадрата со стороной 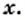 Тогда
Тогда 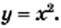
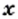 квадрата соответственно будет изменяться и его площадь
квадрата соответственно будет изменяться и его площадь 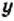 .
.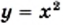 задает функцию.
задает функцию.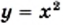 , областью определения которой являются все числа. В таблице приведены некоторые значения аргумента и соответствующие им значения функции.
, областью определения которой являются все числа. В таблице приведены некоторые значения аргумента и соответствующие им значения функции.
 возьмем из таблицы (рис. 11).
возьмем из таблицы (рис. 11).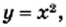 будет отмечено, тем меньше полученная фигура (рис. 12) будет отличаться от графика функции
будет отмечено, тем меньше полученная фигура (рис. 12) будет отличаться от графика функции 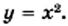
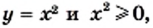 то
то  то есть среди отмеченных точек не может быть точек с отрицательными ординатами.
то есть среди отмеченных точек не может быть точек с отрицательными ординатами.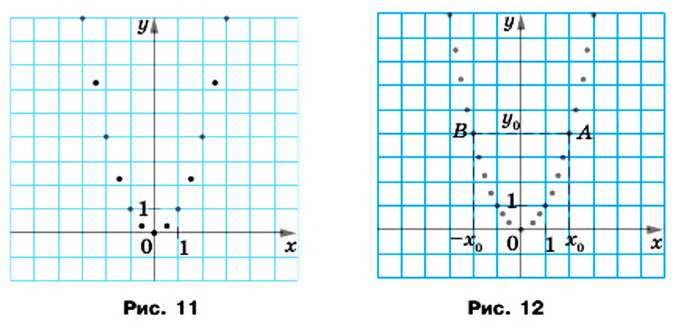
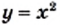 — все неотрицательные числа.
— все неотрицательные числа. то получилась бы фигура — график функции
то получилась бы фигура — график функции  которую называют параболой (рис. 13).
которую называют параболой (рис. 13).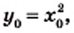 то верно и равенство
то верно и равенство 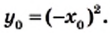 Тогда можно сделать такой вывод: если точка
Тогда можно сделать такой вывод: если точка 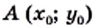 принадлежит параболе
принадлежит параболе 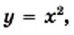 то точка
то точка  также принадлежит этой параболе.
также принадлежит этой параболе.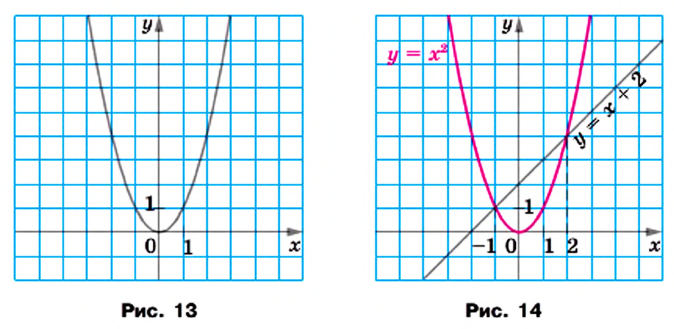
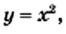 изученные в этом пункте. Область определения Все числа
изученные в этом пункте. Область определения Все числа
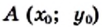 принадлежит параболе
принадлежит параболе 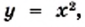 то точка
то точка 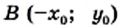 также принадлежит этой параболе.
также принадлежит этой параболе.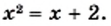
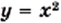 и
и 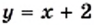 (рис. 14). Эти графики пересекаются в двух точках, абсциссы которых равны 2 и —1. Следовательно, как при
(рис. 14). Эти графики пересекаются в двух точках, абсциссы которых равны 2 и —1. Следовательно, как при 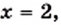 так и при
так и при 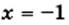 значения выражений
значения выражений 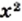 и
и 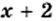 равны, то есть числа 2 и —1 являются корнями уравнения
равны, то есть числа 2 и —1 являются корнями уравнения 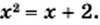 Проверка это подтверждает. Действительно,
Проверка это подтверждает. Действительно, 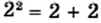 и
и 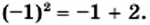
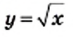 и ее график
и ее график то его сторону
то его сторону  можно найти по формуле
можно найти по формуле 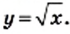 Изменение площади
Изменение площади 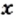 квадрата приводит и к изменению его стороны
квадрата приводит и к изменению его стороны 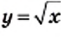 задает функцию.
задает функцию.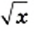 допустимыми значениями переменной
допустимыми значениями переменной 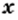 являются все неотрицательные числа, то областью определения функции
являются все неотрицательные числа, то областью определения функции 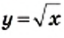 является множество неотрицательных чисел.
является множество неотрицательных чисел.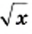 не может принимать отрицательные значения, то есть ни одно отрицательное число не может принадлежать области значений рассматриваемой функции. Покажем, что функция
не может принимать отрицательные значения, то есть ни одно отрицательное число не может принадлежать области значений рассматриваемой функции. Покажем, что функция 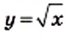 может принимать любые неотрицательные значения, например 7,2. Действительно, существует такое значение аргумента
может принимать любые неотрицательные значения, например 7,2. Действительно, существует такое значение аргумента 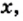 что
что 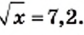 Это значение равно
Это значение равно 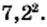 На этом примере мы видим, что для любого неотрицательного числа
На этом примере мы видим, что для любого неотрицательного числа 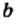 всегда найдется такое значение
всегда найдется такое значение 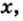 что
что 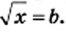 Таким значением аргумента
Таким значением аргумента 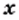 является число
является число 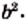
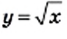 является множество неотрицательных чисел.
является множество неотрицательных чисел.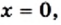 то
то 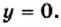
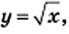 можно сделать вывод, что ее график расположен только в первой координатной четверти.
можно сделать вывод, что ее график расположен только в первой координатной четверти.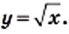

 которых приведены в таблице (рис. 29).
которых приведены в таблице (рис. 29).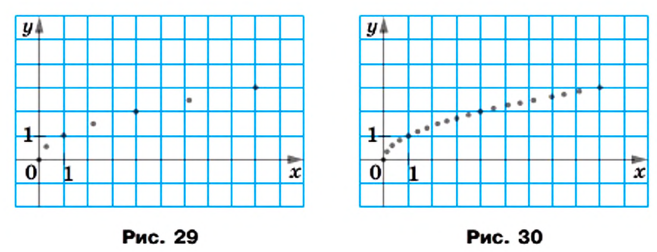
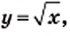 тем меньше полученная фигура будет отличаться от графика функции
тем меньше полученная фигура будет отличаться от графика функции 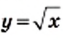 (рис. 30).
(рис. 30).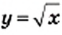 является фигура, равная ветви параболы
является фигура, равная ветви параболы 
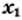 и
и 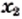 — два произвольных значения аргумента функции
— два произвольных значения аргумента функции 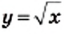 таких, что
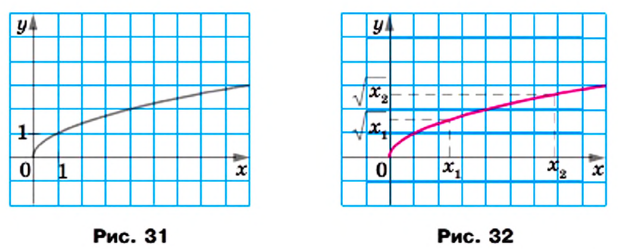
таких, что 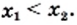 Тогда из свойства арифметического квадратного корня следует, что
Тогда из свойства арифметического квадратного корня следует, что 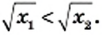
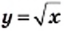 соответствует большее значение функции. Верно и обратное утверждение: большему значению функции соответствует большее значение аргумента, то есть если
соответствует большее значение функции. Верно и обратное утверждение: большему значению функции соответствует большее значение аргумента, то есть если 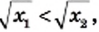 то
то 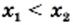 (рис. 32).
(рис. 32).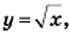 изученные в этом пункте. Область определения Множество неотрицательных чисел
изученные в этом пункте. Область определения Множество неотрицательных чисел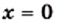
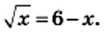
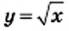 и
и 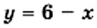 (рис. 33). Эти графики пересекаются в точке, абсцисса которой равна 4. Проверка подтверждает, что число 4 является корнем данного уравнения.
(рис. 33). Эти графики пересекаются в точке, абсцисса которой равна 4. Проверка подтверждает, что число 4 является корнем данного уравнения.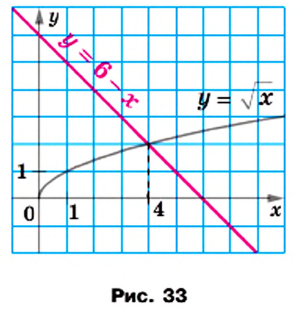
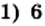 и
и 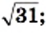 2)
2) 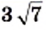 и
и 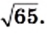
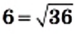 и
и 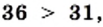 то
то 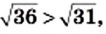 то есть
то есть 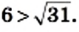
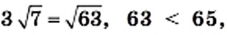
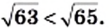
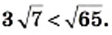
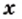 выполняется неравенство
выполняется неравенство 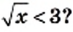
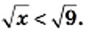 Поскольку большее значение функции
Поскольку большее значение функции 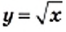 соответствует большему значению аргумента, то можно сделать вывод, что
соответствует большему значению аргумента, то можно сделать вывод, что 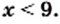 Учитывая, что выражение
Учитывая, что выражение 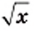 имеет смысл только при
имеет смысл только при 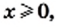 получаем, что данное неравенство выполняется при всех
получаем, что данное неравенство выполняется при всех 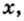 удовлетворяющих неравенству
удовлетворяющих неравенству 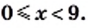
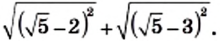
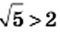 и
и 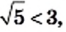 то
то 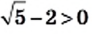 и
и 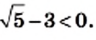
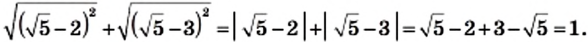
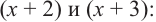
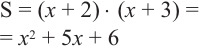

 и длиной
и длиной 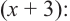
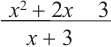
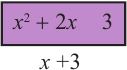
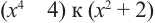 является многочленом, т.к. существует такой многочлен, произведение которого с многочленом
является многочленом, т.к. существует такой многочлен, произведение которого с многочленом 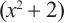 равно
равно 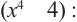
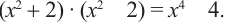
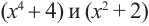 не является многочленом, т.к. нет такого многочлена, произведение которого с
не является многочленом, т.к. нет такого многочлена, произведение которого с 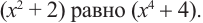
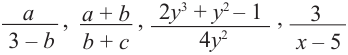
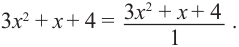 Таким образом, многочлен также является рациональным выражением. Сумма, разность, произведение и отношение рациональных выражений также являются рациональными выражениями, то есть их можно преобразовать в дробь, у которой числитель и знаменатель-некоторые многочлены (в частном случае одночлены).
Таким образом, многочлен также является рациональным выражением. Сумма, разность, произведение и отношение рациональных выражений также являются рациональными выражениями, то есть их можно преобразовать в дробь, у которой числитель и знаменатель-некоторые многочлены (в частном случае одночлены).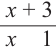 не имеет смысла при
не имеет смысла при 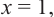 так как при
так как при 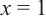 знаменатель превращается в нуль.
знаменатель превращается в нуль.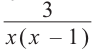
 знаменатель дроби обращается в нуль, надо решить уравнение
знаменатель дроби обращается в нуль, надо решить уравнение 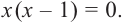 Данное уравнение имеет два корня: 0 и 1. Значит допустимыми значениями являются любые числа, кроме 0 и 1. Для рациональной дроби
Данное уравнение имеет два корня: 0 и 1. Значит допустимыми значениями являются любые числа, кроме 0 и 1. Для рациональной дроби 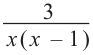 ОДЗ записывается как
ОДЗ записывается как 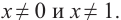
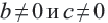 справедливо следующее равенство
справедливо следующее равенство 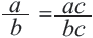 , а это значит, что данная дробь умножается на дробь
, а это значит, что данная дробь умножается на дробь 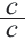 , т.е. на 1. Аналогичное свойство верно и для рациональных выражений. При умножении или делении числителя и знаменателя рационального выражения на одно и то же отличное от нуля выражение, получается дробь,эквивалентная данному выражению при всех допустимых значениях переменной.
, т.е. на 1. Аналогичное свойство верно и для рациональных выражений. При умножении или делении числителя и знаменателя рационального выражения на одно и то же отличное от нуля выражение, получается дробь,эквивалентная данному выражению при всех допустимых значениях переменной.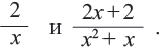
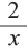 на выражение
на выражение 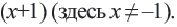 Получим
Получим 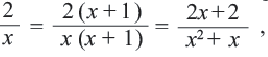
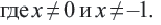
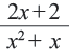 на выражение
на выражение 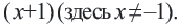 Получим
Получим 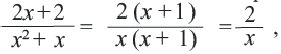
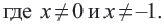
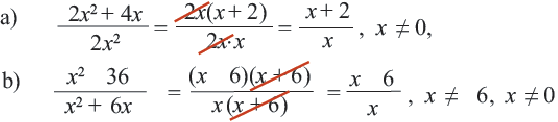
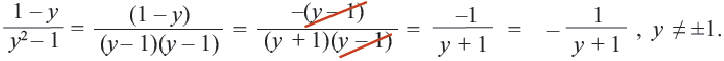
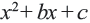 возможно найти такие числа
возможно найти такие числа 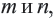 чтобы их произведение было равно
чтобы их произведение было равно 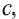 а сумма была равна
а сумма была равна 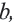 то в этом случае:
то в этом случае: 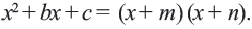
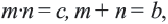 тогда можно записать, что
тогда можно записать, что 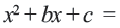
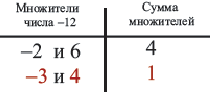
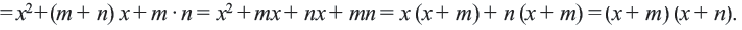 Понятно что, если
Понятно что, если 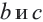 являются целыми числами, то числа
являются целыми числами, то числа 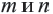 надо искать среди делителей числа
надо искать среди делителей числа 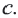
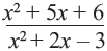 сначала надо разложить числитель и знаменатель на множители.
сначала надо разложить числитель и знаменатель на множители.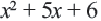 надо найти два положительных числа, произведение которых равно 6, а сумма 5. Это числа 2 и 3:
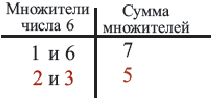
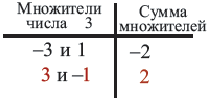
надо найти два положительных числа, произведение которых равно 6, а сумма 5. Это числа 2 и 3: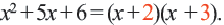
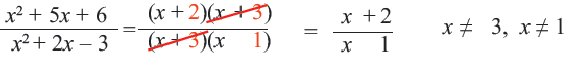
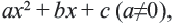 надо найти такие
надо найти такие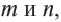 чтобы
чтобы 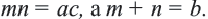 Тогда
Тогда 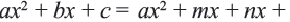
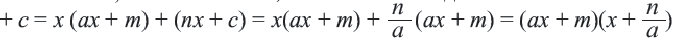
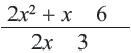
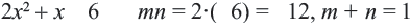
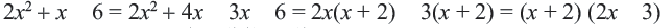

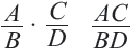
 некоторые многочлены
некоторые многочлены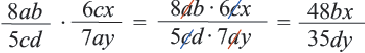
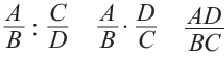
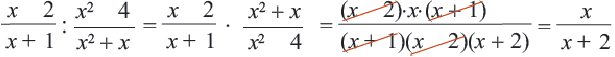
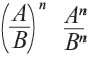
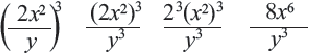
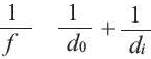
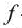 — фокусное расстояние,
— фокусное расстояние,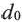 — расстояние от объекта до линзы фотоаппарата,
— расстояние от объекта до линзы фотоаппарата,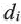 — расстояние от линзы фотоаппарата до ленты.
— расстояние от линзы фотоаппарата до ленты.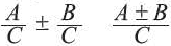 здесь
здесь  некоторые многочлены
некоторые многочлены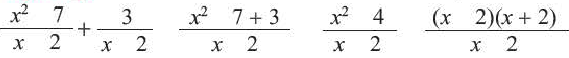
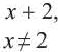
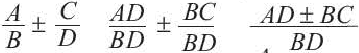 здесь
здесь  некоторые многочлены
некоторые многочлены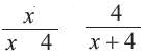
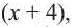 а числитель и знаменатель второй дроби на
а числитель и знаменатель второй дроби на 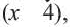 приведём дроби к общему знаменателю, а затем выполним вычитание.
приведём дроби к общему знаменателю, а затем выполним вычитание.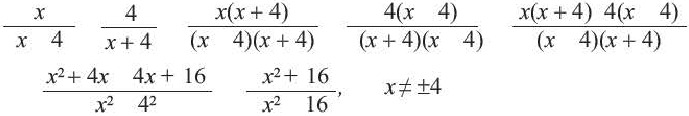
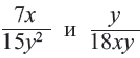
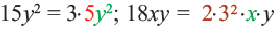
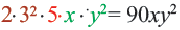
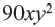 и выполним сложение.
и выполним сложение.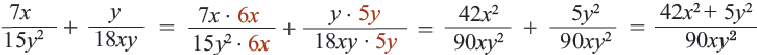
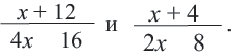

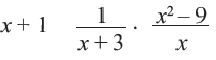
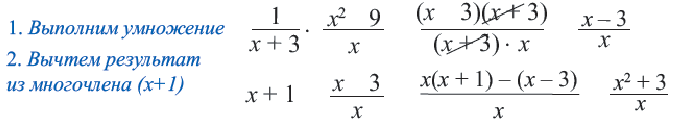

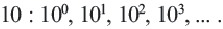 В этой строке каждое число в 10 раз меньше следующего. Если продолжить запись влево, в соответствии с данным правилом, то получим следующее: перед числом
В этой строке каждое число в 10 раз меньше следующего. Если продолжить запись влево, в соответствии с данным правилом, то получим следующее: перед числом 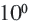 стоит число
стоит число 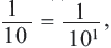 перед числом
перед числом 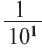 число
число 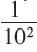 и т.д.
и т.д. 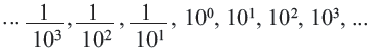
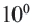 справа, на единицу меньше степени следующего числа. Примен ив данное правило к числам, стоящим слева от числа
справа, на единицу меньше степени следующего числа. Примен ив данное правило к числам, стоящим слева от числа 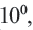 получим отрицательные степени числа 10, которые запишем так: вместо
получим отрицательные степени числа 10, которые запишем так: вместо 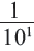 запишем
запишем 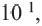 вместо
вместо 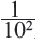 запишем
запишем 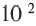 и т.д.
и т.д.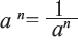 при
при 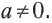
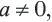
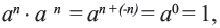 а отсюда получим,
а отсюда получим, 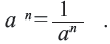
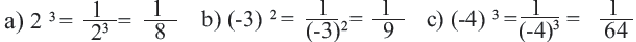
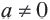 и любых целых чисел
и любых целых чисел 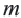 и
и 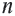 справедливы равенства
справедливы равенства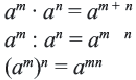
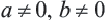 и для любого целого числа
и для любого целого числа 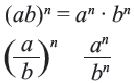
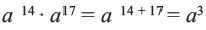
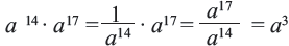
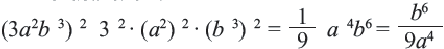
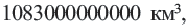 а диаметр молекулы очень маленьким числом
а диаметр молекулы очень маленьким числом 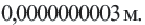 Большие и малые числа неудобно записывать в виде обыкновенных или десятичных дробей и выполнять какие-либо действия над ними. В этом случае их представляют в виде
Большие и малые числа неудобно записывать в виде обыкновенных или десятичных дробей и выполнять какие-либо действия над ними. В этом случае их представляют в виде 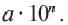
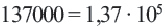 или
или 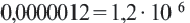
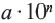 называется стандартным видом числа, где
называется стандартным видом числа, где 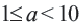 и
и 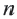 целое число, число
целое число, число 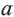 называется значащей частью,
называется значащей частью, 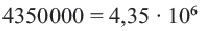 (порядок равен 6).
(порядок равен 6).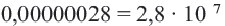 (порядок равен 7).
(порядок равен 7).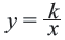 и ее график
и ее график Выразив длину через
Выразив длину через 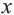 см, а ширину через
см, а ширину через  см, эту зависимость можно записать в виде
см, эту зависимость можно записать в виде 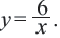 Так как в данном задании
Так как в данном задании 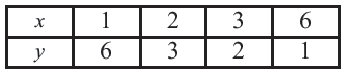
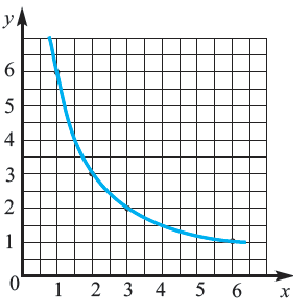
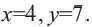 Запишите формулу данной зависимости. Так как произведение переменных, связанных обратно пропорциональной зависимостью, всегда остаётся постоянным, то обозначим эту постоянную через
Запишите формулу данной зависимости. Так как произведение переменных, связанных обратно пропорциональной зависимостью, всегда остаётся постоянным, то обозначим эту постоянную через 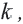 тогда
тогда 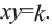 В нашем случае
В нашем случае 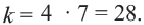 Тогда соответствующую зависимость можно записать в виде формулы так:
Тогда соответствующую зависимость можно записать в виде формулы так: 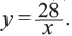
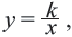 в которой переменная принимает как положительные, так и отрицательные значения.
в которой переменная принимает как положительные, так и отрицательные значения.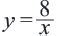 и построим её график.
и построим её график.
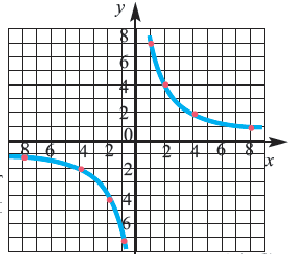
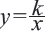 называется обратно пропорциональной функцией.
называется обратно пропорциональной функцией.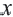 — независимая переменная,
— независимая переменная, 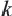 — число отличное от нуля. Функция
— число отличное от нуля. Функция 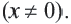
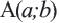 принадлежит графику функции
принадлежит графику функции 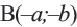 также принадлежит графику функции. График функции
также принадлежит графику функции. График функции 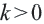 ветви гиперболы расположены в I и II1 четверти, а при
ветви гиперболы расположены в I и II1 четверти, а при 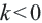 расположены во II и IV четверти. Чем больше абсолютное значение абсциссы на графике, тем ближе эта точка расположена к оси абсцисс.
расположены во II и IV четверти. Чем больше абсолютное значение абсциссы на графике, тем ближе эта точка расположена к оси абсцисс.