Что такое движение материальной точки
Основы механики для чайников. Часть 1: Кинематика
В прошлой статье мы немножко разобрались с тем, что такое механика и зачем она нужна. Мы уже знаем, что такое система отсчета, относительность движения и материальная точка. Что ж, пора двигаться дальше! Здесь мы рассмотрим основные понятия кинематики, соберем вместе самые полезные формулы по основам кинематики и приведем практический пример решения задачи.
Присоединяйтесь к нам в телеграм и получайте ежедневную рассылку с полезной информацией по актуальным студенческим вопросам.
Траектория, радиус-вектор, закон движения тела
Кинематикой занимался еще Аристотель. Правда, тогда это не называлось кинематикой. Затем очень большой вклад в развитие механики, и кинематики в частности, внес Галилео Галилей, изучавший свободное падение и инерцию тел.
Итак, кинематика решает вопрос: как тело движется. Причины, по которым оно пришло в движение, ее не интересуют. Кинематике не важно, сама поехала машина, или ее толкнул гигантский динозавр. Абсолютно все равно.
Сейчас мы будем рассматривать самую простую кинематику – кинематику точки. Представим, что тело (материальная точка) движется. Не важно, что это за тело, все равно мы рассматриваем его, как материальную точку. Может быть, это НЛО в небе, а может быть, бумажный самолетик, который мы запустили из окна. А еще лучше, пусть это будет новая машина, на которой мы едем в путешествие. Перемещаясь из точки А в точку Б, наша точка описывает воображаемую линию, которая называется траекторией движения. Другое определение траектории – годограф радиус вектора, то есть линия, которую описывает конец радиус-вектора материальной точки при движении.
Радиус-вектор – вектор, задающий положение точки в пространстве.
Для того, чтобы узнать положение тела в пространстве в любой момент времени, нужно знать закон движения тела – зависимость координат (или радиус-вектора точки) от времени.
Перемещение и путь
Тело переместилось из точки А в точку Б. При этом перемещение тела – отрезок, соединяющий данные точки напрямую – векторная величина. Путь, пройденный телом – длина его траектории. Очевидно, перемещение и путь не стоит путать. Модуль вектора перемещения и длина пути совпадают лишь в случае прямолинейного движения.
В системе СИ перемещение и длина пути измеряются в метрах.
Перемещение равно разнице радиус-векторов в начальный и конечный моменты времени. Другими словами, это приращение радиус вектора.
Скорость и ускорение
Средняя скорость – векторная физическая величина, равная отношению вектора перемещения к промежутку времени, за которое оно произошло
А теперь представим, что промежуток времени уменьшается, уменьшается, и становится совсем коротким, стремится к нулю. В таком случае о средней скорости говорить на приходится, скорость становится мгновенной. Те, кто помнит основы математического анализа, тут же поймут, что в дальнейшем нам не обойтись без производной.
Мгновенная скорость – векторная физическая величина, равная производной от радиус вектора по времени. Мгновенная скорость всегда направлена по касательной к траектории.
В системе СИ скорость измеряется в метрах в секунду
Если тело движется не равномерно и прямолинейно, то у него есть не только скорость, но и ускорение.
Ускорение (или мгновенное ускорение) – векторная физическая величина, вторая производная от радиус-вектора по времени, и, соответственно, первая производная от мгновенной скорости
Ускорение показывает, как быстро изменяется скорость тела. В случае прямолинейного движения, направления векторов скорости и ускорения совпадают. В случае же криволинейного движения, вектор ускорения можно разложить на две составляющие: ускорение тангенциальное, и ускорение нормальное.
Тангенциальное ускорение показывает, как быстро изменяется скорость тела по модулю и направлено по касательной к траектории
Нормальное же ускорение характеризует быстроту изменения скорости по направлению. Векторы нормального и тангенциального ускорения взаимно перпендикулярны, а вектор нормального ускорения направлен к центру окружности, по которой движется точка.
Здесь R – радиус окружности, по которой движется тело.
Закон равноускоренного движения
Рассмотрим далее закон равноускоренного движения, то есть движения с постоянным ускорением. Будем рассматривать простейший случай, когда тело движется вдоль оси x.
Производная по скорости от времени даст значение ускорения a, которое является константой.
Пример решения задачи
Теперь, когда мы рассмотрели физические основы кинематики, пора закрепить знания на практике и решить какую-нибудь задачу. Причем, чем быстрее, тем лучше.
Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.
Решим такую задачу: точка движется по окружности радиусом 4 метра. Закон ее движения выражается уравнением S=A+Bt^2. А=8м, В=-2м/с^2. В какой момент времени нормальное ускорение точки равно 9 м/с^2? Найти скорость, тангенциальное и полное ускорение точки для этого момента времени.
Решение: мы знаем, что для того, чтобы найти скорость нужно взять первую производную по времени от закона движения, а нормальное ускорение равняется частному квадрата скорости и радиуса окружности, по которой точка движется. Вооружившись этими знаниями, найдем искомые величины.
Нужна помощь в решении задач? Профессиональный студенческий сервис готов оказать ее.
Уравнение движения материальной точки
Движение материальной точки в пространстве – это изменение ее положения относительно других тел с течением времени.
Имеет смысл говорить только о движении в некоторой системе отсчета.
Система отсчета. Системы координат
Точки, располагаемые в пустом пространстве, не различаются. Поэтому о точке рассуждают при условии нахождения в ней материальной точки. Определить ее положение можно при помощи измерений в системе координат, где и проводится нахождение пространственных координат. Если рассматривать в виде примера поверхность Земли, то следует учитывать широту и долготу располагаемой точки.
В теории зачастую не принимают во внимание реальную систему отсчета, а сохраняют только ту, которая представляет собой ее математическую модель, применяемую во время практических измерений.
Кинематическое уравнение движения материальной точки
Любая система отсчета или координат предполагает определение координат материальной точки в любой момент времени.
При условии положения и определения материальной точки в данной системе отсчета считается, что ее движение задано или описано.
Это возможно при использовании кинематического уравнения движения:
Аналитически положение точки определяется совокупностью трех независимых между собой чисел. Иначе говоря, свободная точка имеет три степени свободы движения.
Равенства ( 2 ) считают кинематическими уравнениями движения материальной точки в декартовых координатах.
Определение движения точки возможно с помощью задания траектории и мгновенного положения точки на ней. Ее положение на кривой определяется с помощью указания только одной величины: расстояния вдоль кривой от некоторой начальной точки с положительным направлением:
Это и есть уравнение движения точки по траектории. Способ его задания относят к естественному или траекторному.
Понятия координатного и естественного способа задания движения точки физически эквивалентны. С математической стороны это рассматривают как возможность применения разных методов, исходя из случая математической задачи.
Задание такого закона возможно аналитическим, графическим путем или с использованием таблицы, последние два из которых зачастую рассматривают в виде графиков и расписаний движений поездов.
Решение
При решении необходимо учитывать зависимость скорости от времени:
Зависимость координаты от времени и сравнение уравнения с заданным принимает вид:
После подстановки данных в уравнение:
Определим точки, изобразим график:
Путь, по которому двигалось тело, равняется площади фигуры, ограниченной графиком, и находится с помощью формулы:
Уравнение движения материальной точки
Что такое движение материальной точки
В механике рассматривают перемещение объектов. Принципы характерны для материальной точки и твердого тела. Термин «материальная точка» введен с целью упростить решение практических задач. В случае, когда габариты объекта существенно меньше, чем расстояние, которое он преодолевает, либо размеры других тел, то условно данный объект обозначают материальной точкой.
Кинематика — раздел механики, изучающий математическое описание движения идеализированных тел, без рассмотрения причин движения.
Движением материальной точки в пространстве называют изменение ее положения по отношению к другим телам с течением времени.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Для расчета физических характеристик самолета относительно Земли в полете можно представить его в виде материальной точки. Однако если рассматривается система, которая включает самолет и пассажира, летящего в нем, то в данном случае принимать транспортное средство за материальную точку нецелесообразно. Таким образом, движение материальной точки рассматривают только в том случае, когда размерами объекта в конкретной ситуации можно пренебречь.
В одинаковое время положение точки в пространстве может отличаться в зависимости от того, относительно какого тела осуществляются наблюдения. С помощью системы координат и тела отсчета описывают перемещение материальной точки в пространстве. Согласно элементарным математическим закономерностям, задать положение какой-либо точки на плоскости можно, воспользовавшись системой координат.
Прямые, которые взаимно перпендикулярны и пересекаются в одной точке, являются координатными прямыми. А данная точка пересечения носит название начала координат.
Из начала координат можно вывести еще одну прямую, которая будет являться перпендикуляром к плоскости. Подобная система позволит задать положение точки в пространстве. Другим методом является применение радиус-вектора.
Радиус-вектор представляет собой отрезок, который провели из точки начала координат к заданной точке.
В течение времени движущаяся материальная точка меняет свое положение в пространстве. Для того чтобы выполнить расчет положения точки в какой-либо определенный момент времени, необходимо провести измерения времени.
Совокупность тела отсчета, связанной с ним системы координат и прибора отсчета времени представляет собой систему отсчета.
Выбор системы отсчета определяется следующими характеристиками:
Можно рассмотреть движение двух автомобилей, которые находятся на соседних полосах и перемещаются в одном направлении с равными скоростями. Когда телом отсчета является одно из этих транспортных средств, при заданной системе отсчета скорость, путь и перемещение второго транспорта будут иметь нулевые значения. Таким образом, второй автомобиль по сравнению с первым находится в состоянии покоя. В случае, когда в качестве тела отсчета выбрана дорога, значения скорости, пути и перемещения будут отличны от нуля.
Траектория материальной точки — линия, которую очерчивает материальная точка, двигаясь в пространстве.
Траектория включает множество точек, в которых рассматриваемая материальная точка была зафиксирована в прошедший момент времени, находится в данное время и будет замечена в будущий временной период.
Перемещением материальной точки называют вектор, берущий начало в точке траектории в начальный промежуток времени и заканчивающийся в точке траектории в конечный момент времени.
Путь материальной точки представляет собой сумму всех отрезков, пройденных материальной точкой в процессе движения.
Путем называют скалярную величину, которая всегда характеризуется положительным значением. При перемещении материальной точки пройденный ей путь может только увеличиваться.
Амплитуда — максимальное значение смещения или изменения переменной величины от среднего значения при колебательном или волновом движении.
Система отсчета и координат
Точки, которые присутствуют в пустом пространстве, не различают. Рассуждать о точке целесообразно, когда в ней находится материальная точка. Система координат позволяет выполнить измерения, которые необходимы для вычисления пространственных координат. Исходя из полученных данных, определяют положение материальной точки в пространстве. В качестве примера можно рассмотреть поверхность нашей планеты. Тогда для определения положения необходимо вычислить широту и долготу заданной точки.
В теоретических расчетах применяют декартову прямоугольную систему координат. С ее помощью можно определить положение точки при условии наличия радиус-вектора \(\bar
Другие способы решения задачи на определение положения материальной точки:
В теоретических расчетах, как правило, пренебрегают реальной системой отсчета. Обычно для измерений используют ту систему, которая является математической моделью реальной, применяемой для практических исследований.
Какому закону подчиняется движение точки в пространстве
Кинематические законы движения
Механическое движение представляет собой изменение положения тела по отношению к другим телам, входящим в систему отсчета. Для описания движения тела выбирают систему отсчета, состоящую из следующих компонентов:
Основными способами описания движения тела являются:
Если тело рассматривают в рамках декартовой системы координат, то положение материальной точки М определяется с помощью радиус-вектора \(\bar
Во время движения материальной точки фиксируют изменение ее координат:
С помощью данных формул можно рассчитать перемещение точки координатным методом. Радиус-вектор будет определяться, согласно следующему уравнению:
где \(\bar, \bar
Векторное кинетическое уравнение движения материальной точки будет записано таким образом:
Представленные уравнения являются кинетическими законами движения материальной точки. Эти закономерности необходимы для полноценного описания перемещения токи в пространстве. Найти модуль или длину радиус-вектора можно с помощью формулы:
Динамические законы движения материальной точки
В динамике движение материальной точки рассматривают, исходя из воздействия сил, приложенных к рассматриваемой точке. Ключевые закономерности классической динамики сформулировал Ньютон.
Первый закон Ньютона определяет тот факт, что материальная точка находится в состоянии покоя или перемещается равномерно и прямолинейно при отсутствии воздействия на нее внешних сил или, когда действие этих сил взаимно скомпенсировано.
Второй закон Ньютона гласит, что для инерционных систем отсчета результирующая сил, которые приложены к материальной точке, равна произведению ее массы и ускорения.
В виде формулы второй закон Ньютона можно записать следующим образом:
Дифференциальные уравнения для перемещения материальной точки записывают в таком виде:
где х, у, z являются координатами движущейся материальной точки,
\(
Согласно дифференциальным уравнениям движения материальной точки, зная массу, можно найти силы, которые оказывают на рассматриваемую точку воздействие.
Кинематическое уравнение движения материальной точки
В любой системе отсчета или координат можно определить координаты материальной точки в разные моменты времени. Если определены положение и материальная точка в какой-либо системе отсчета, ее перемещение называют заданным или описанным. Такое условие соблюдается, благодаря применению кинематического уравнения движения:
Аналитическим положением точки является совокупность трех чисел, которые не зависят друг от друга, то есть трех степеней свободы движения.
При наличии указанного положения в любой момент времени t считается, что движение точки, согласно первому уравнению, определено. В этом случае необходимо задать декартовы координаты точки в виде однозначных и непрерывных функций времени:
Прямоугольными декартовыми координатами x, y, z являются проекции радиус-вектора, который выведен из начала координатной системы. Понятно, что длина и направление радиус-вектора рассчитывается из соотношений, в которых a, β, γ представляют собой углы с координатными осями, которые образованы радиус-вектором. Таким образом, кинематическими уравнениями движения материальной точки в декартовых координатах будут следующие равенства:
Данные формулы можно записать с помощью другой системы координат, связанной с декартовой по средствам однозначных преобразований. В случае, когда точка перемещается в плоскости Оху, можно воспользоваться полярными координатами r, ϕ, которые относятся к декартовым преобразованиям. При этом используют формулу движения точки, записанную следующим образом:
Кинематическое уравнение для описания перемещения точки в криволинейных координатах q1, q2, q3, которые связаны с декартовыми преобразованиями:
будет представлено в следующей форме:
Кривая радиус-вектора, которую описывает конец вектора в процессе перемещения точки, совпадает с ее траекторией. Параметрическим уравнением траектории с t являются следующие равенства:
Исключая время из кинематических уравнений, получают вид координатного уравнения траектории. Для того чтобы определить движение точки, необходимо задать ее траекторию и мгновенное положение точки на ней. Положение точки на кривой рассчитывают по средствам лишь одной характеристики, которой является расстояние вдоль кривой от некого начала отсчета с положительным направлением:
Данная формула представляет собой уравнение движения точки по траектории. Метод его записи является естественным или траекторным. Установлена физическая эквивалентность понятий координатного и естественного метода задания движения материальной точки. С точки зрения математики, данное положение представляет собой возможность использования разных методик в зависимости от конкретных условий задачи. Задать такую закономерность можно с помощью аналитических, графических или табличных средств.
Движение материальной точки

Всего получено оценок: 145.
Всего получено оценок: 145.
Движение – форма существования материи. Рассмотрим понятие движения материальной точки.
Материальная точка
Поэтому при решении задач имеет смысл заменить исследуемое тело некоей абстрактной моделью, которая бы содержала только важные для данной задачи характеристики.
В случае задач механики такими характеристиками являются координаты тела и его масса. Если из анализа условий задачи видно, что разницей движения различных точек тела можно пренебречь (или все точки будут двигаться одинаково), то тело заменяется только одной точкой, которой приписывается вся масса тела, и расчеты выполняются именно для этой точки. Такая точка называется «материальной точкой».
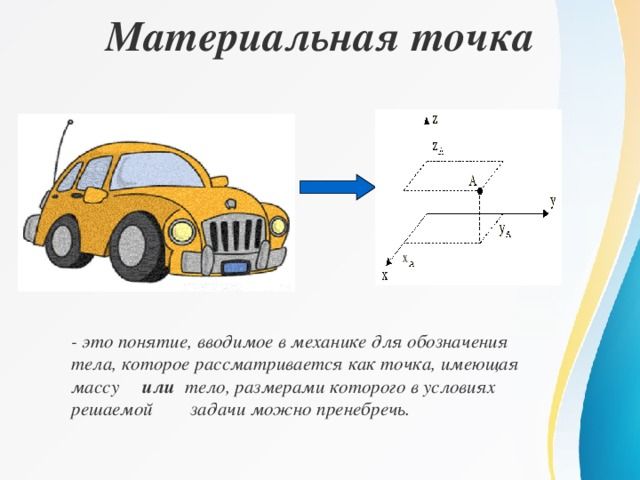
Описание движения материальной точки
Координаты в Системе Отсчета
Поскольку движение материальной точки состоит в том, что она меняет свои координаты в принятой Системе Отсчета с течением времени, для описания движения можно вывести закон, некоторую формулу, в которой переменной величиной будет время. В результате, становится возможным получать значение координаты материальной точки в любой заданный момент времени.
Примером такой формулы является закон движения материальной точки при равноускоренном движении:
$$\overrightarrow x=\overrightarrow x_0+\overrightarrow v_0t+<\overrightarrow at^2\over 2>$$
Траектория пути
Описание движения с помощью формул дает высокую точность, но не всегда достаточно наглядно.
Форма пути, проходимого телом (в данном случае – орбиты) называется траекторией пути, или просто траекторией. Анализ траектории пути, наряду с формульным описанием движения, позволяет точнее представить себе особенности рассматриваемой задачи.
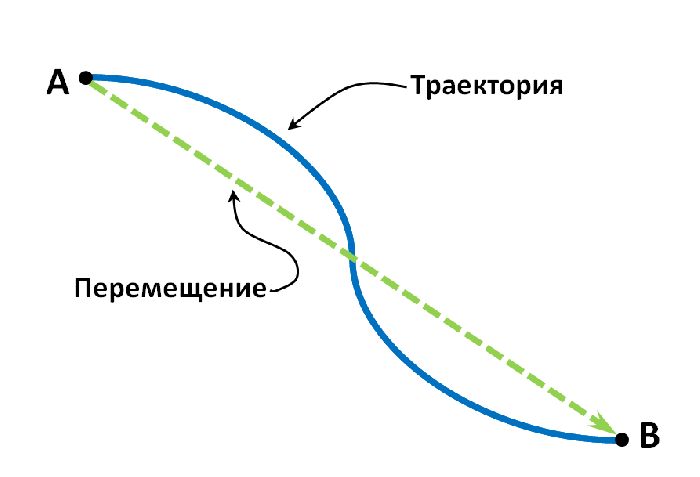
Прямолинейные и криволинейные движения
По форме траектории механические движения можно разделить на прямолинейные и криволинейные. Наиболее простыми движениями являются прямолинейные. Для таких движений следует, по возможности, выбирать Систему Отсчета с одной координатной осью, параллельную траектории.
Криволинейные движения значительно сложнее. Во-первых, для их описания, как правило, требуется две или три оси координат. Во-вторых, если прямолинейное движение может происходить с постоянной скоростью, то во время криволинейного движения скорость обязательно меняется. Даже если модуль скорости остается постоянным – меняется ее направление, что при проецировании на оси координат обязательно даст изменение проекций скоростей, и это усложняет формулы.
Что мы узнали?
Для описания движения тел пользуются понятием материальной точки. Движение материальной точки может быть описано с помощью формул и с помощью траектории пути.
Механическое движение и его характеристики
теория по физике 🧲 кинематика
Механика — раздел физики, который изучает механическое движение физических тел и взаимодействие между ними.
Основная задача механики — определение положение тела в пространстве в любой момент времени.
Механическое движение — изменение положения тела в пространстве относительно других тел с течением времени.
Механическое движение и его виды
По характеру движения точек тела выделяют три вида механического движения:
По типу линии, вдоль которой движется тело, выделяют два вида движения:
По скорости выделяют два вида движения:
По ускорению выделяют три вида движения:
Что нужно для описания механического движения?
Для описания механического движения нужно выбрать, относительно какого тела оно будет рассматриваться. Движение одного и того же объекта относительно разных тел неодинаковое. К примеру, идущий человек относительно дерева движется с некоторой скоростью. Но относительно сумки, которую он держит в руках, он находится в состоянии покоя, так как расстояние между ними с течением времени не изменяется.
Решение основной задачи механики — определения положения тела в пространстве в любой момент времени — заключается в вычислении координат его точек. Чтобы вычислить координаты тела, нужно ввести систему координат и связать с ней тело отсчета. Также понадобится прибор для измерения времени. Все это вместе составляет систему отсчета.
Система отсчета — совокупность тела отсчета и связанных с ним системы координат и часов.
Тело отсчета — тело, относительно которого рассматривается движение.
Часы — прибор для отсчета времени. Время измеряется в секундах (с).
При описании движения тела важно учитывать его размеры, так как характер движения его отдельных точек может различаться. Но в рамках некоторых задач размер тела не влияет на результат решения. Тогда его можно считать пренебрежительно малым. Тогда тело рассматривают как движущуюся материальную точку.
Материальная точка — это тело, размерами которого можно пренебречь в условиях конкретной задачи. Допустимо принимать тело за точку, если оно движется поступательно или его размеры намного меньше расстояний, которые оно проходит.
Виды систем координат
В зависимости от характера движения тела для его описания выбирают одну из трех систем координат:
Способы описания механического движения
Описать механическое движение можно двумя способами:
Координатный способ
Указать положение материальной точки в пространстве можно, используя трехмерную систему координат. Если эта точка движется, то ее координаты с течением времени меняются. Так как координаты точки зависят от времени, можно считать, что они являются функциями времени. Математически это записывается так:
Эти уравнения называют кинематическими уравнениями движения точки, записанными в координатной форме.
Векторный способ
Радиус-вектор точки — вектор, начало которого совпадает с началом системы координат, а конец — с положением этой точки.
Указать положение точки в трехмерном пространстве также можно с помощью радиус-вектора. При движении точки радиус-вектор со временем изменяется. Он может менять направление и длину. Это значит, что радиус-вектор тоже можно принять за функцию времени. Математически это записывается так:
Эта формула называется кинематическим уравнением движения точки, записанным в векторной форме.
Характеристики механического движения
Движение материальной точки характеризуют три физические величины:
Перемещение
Траектория — линия, которую описывает тело во время движения.
Путь — длина траектории. Обозначается буквой s. Единица измерения — метры (м).
Путь есть функция времени:
Модуль перемещения — длина вектора перемещения. Обозначается как |Δ r |. Единица измерения — метры (м).
Модуль перемещения необязательно должен совпадать с длиной пути.
Пример №1. Человек обошел круглое поле диаметром 1 км. Чему равны пройденный путь и перемещение, которое он совершил.
Путь равен длине окружности. Поэтому:
Человек, обойдя круглое поле, вернулся в ту же точку. Поэтому его начальное положение совпадает с конечным. В этом случае человек совершил перемещение, равное нулю.
Пример №2. Точка движется по окружности радиусом 10 м. Чему равен путь, пройденный этой точкой, в момент, когда модуль перемещения равен диаметру окружности?
Диаметр — это отрезок, который соединяет две точки окружности и проходит через центр. Перемещение равно длине этого отрезка в случае, если один из концов этого отрезка является началом вектора перемещения, а другой — его концом. Траекторией движения в этом случае является дуга, равная половине окружности. А длина траектории есть путь:
Скорость
Скорость — векторная физическая величина, характеризующая быстроту перемещения тела. Численно она равна отношению перемещения за малый промежуток времени к величине этого промежутка.
Скорость характеризуется не только направлением вектора скорости, но и его модулем.
Модуль скорости — расстояние, пройденное точкой за единицу времени. Обозначается буквой V и измеряется в метрах в секунду (м/с).
Математическое определение модуля скорости:
Величина скорости тела в данный момент времени есть первая производная от пройденного пути по времени:
Ускорение
Ускорение — векторная физическая величина, которая характеризует быстроту изменения скорости тела. Численно она равна отношению изменения скорости за малый промежуток времени к величине этого промежутка.
Модуль ускорения — численное изменение скорости в единицу времени. Обозначается буквой a. Единица измерения — метры в секунду в квадрате (м/с 2 ).
Математическое определение модуля скорости:

Ускорение тела есть первая производная от скорости или вторая производная от пройденного пути по времени:
Проекция вектора перемещения на ось координат
Проекция вектора перемещения на ось — это скалярная величина, численно равная разности конечной и начальной координат.
Проекция вектора на ось OX:
Проекция вектора на ось OY:
Знаки проекций перемещения
Проекция вектора перемещения на ось считается нулевой, если вектор расположен перпендикулярно этой оси.
Модуль перемещения — длина вектора перемещения:
Модуль перемещения измеряется в метрах (м).
Вместе с собственными проекциями модуль перемещения образует прямоугольный треугольник. Сам он является гипотенузой этого треугольника. Поэтому для его вычисления можно применить теорему Пифагора. Выглядит это так:
Выразив проекции вектора перемещения через координаты, эта формула примет вид:
Выражение проекций вектора перемещения через угол его наклона по отношению к координатным осям:
Общий вид уравнений координат:
Пример №3. Определить проекции вектора перемещения на ось OX, OY и вычислить его модуль.
Определяем координаты начальной точки вектора:
Определяем координаты конечной точки вектора:
Проекция вектора перемещения на ось OX:
Проекция вектора перемещения на ось OY:
Применяем формулу для вычисления модуля вектора перемещения:
Пример №4. Определить координаты конечной точки B вектора перемещения, если начальная точка A имеет координаты (–5;5). Учесть, что проекция перемещения на OX равна 10, а проекция перемещения на OY равна 5.
Извлекаем известные данные:
Для определения координаты точки В понадобятся формулы:
Выразим из них координаты конечного положения точки:
Точка В имеет координаты (5; 10).
Алгоритм решения
Решение
Записываем исходные данные:
Записываем формулу ускорения:
Так как начальная скорость равна 0, эта формула принимает
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
Отсюда скорость равна:
Подставляем имеющиеся данные и вычисляем:
pазбирался: Алиса Никитина | обсудить разбор | оценить













































