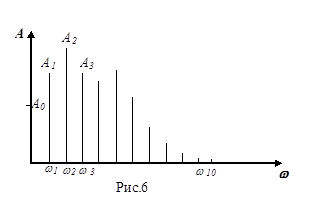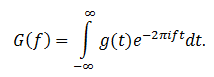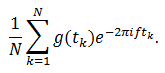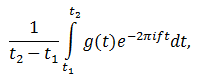Что такое гармоники в ряде фурье
Гармонические колебания
На хабре было несколько статей по преобразованию Фурье и о всяких красивостях типа Цифровой Обработки Сигналов (ЦОС), но неискушённому пользователю совершенно не понятно, зачем всё это нужно и где, а главное как это применить.

АЧХ шума.
Лично мне после прочтения этих статей (например, этой ) не стало понятно, что это и зачем оно нужно в реальной жизни, хотя было интересно и красиво.
Хочется не просто поглядеть красивые картинки, а так сказать, ощутить нутром, что и как работает. И я приведу конкретный пример с генерацией и обработкой звуковых файлов. Можно будет и послушать звук, и поглядеть его спектр, и понять, почему это так.
Статья не будет интересна тем, кто владеет теорией функций комплексной переменной, ЦОС и прочими страшными темами. Она скорее для любопытствующих, школьников, студентов и им сочувствующих :).
Сразу оговорюсь, я не математик, и многие вещи могу даже сказать неправильно (поправляйте личным сообщением), и данную статью пишу, опираясь на собственный опыт и собственное понимание текущих процессов. Если вы готовы, то поехали.
Пару слов о матчасти
Если мы вспомним школьный курс математики, то для построения графика синуса мы использовали круг. В общем-то так и получается, что вращательное движение можно превратить в синусоиду (как и любое гармоническое колебание). Самое лучшая иллюстрация этого процесса приведена в википедии

Гармонические колебания
Т.е. фактически график синуса получается из вращения вектора, который описывается формулой:
где A — длина вектора (амплитуда колебаний), φ — начальный угол (фаза) вектора в нулевой момент времени, ω — угловая скорость вращения, которая равна:
ω=2 πf, где f — частота в Герцах.
Как мы видим, что зная частоту сигнала, амплитуду и угол, мы можем построить гармонический сигнал.
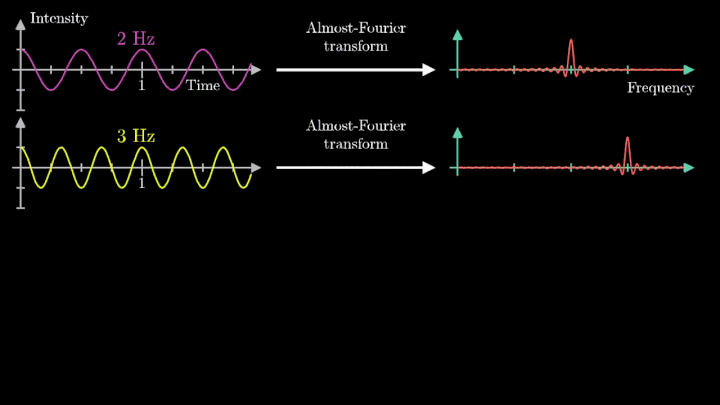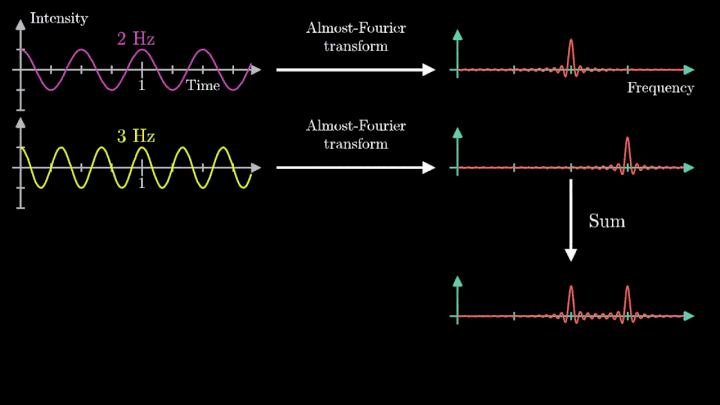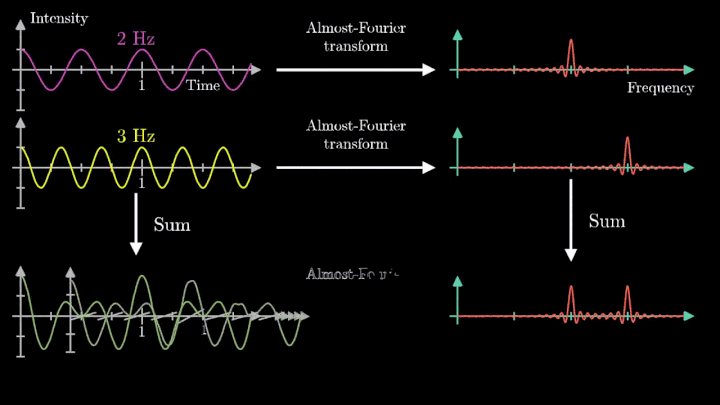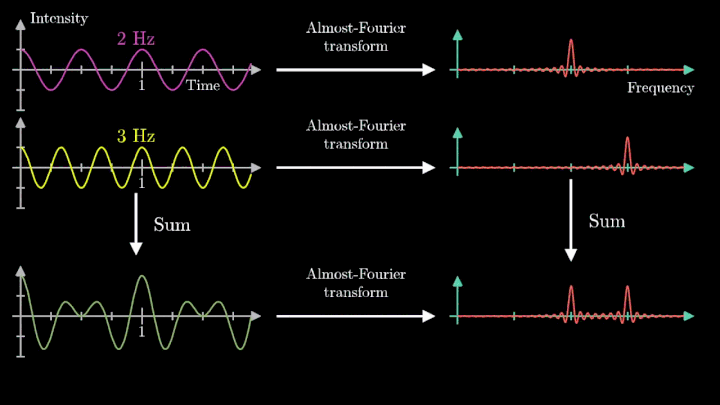
Магия начинается тогда, когда оказывается, что представление абсолютно любого сигнала можно представить в виде суммы (зачастую бесконечной) различных синусоид. Иначе говоря, в виде ряда Фурье.
Я приведу пример из английской википедии. Для примера возьмём пилообразный сигнал.

Пилообразный сигнал
Его сумма будет представлена следующей формулой:
Если мы будем по очерёдно суммировать, брать сначала n=1, затем n=2 и т.д., то увидим, как у нас гармонический синусоидальный сигнал постепенно превращается в пилу:
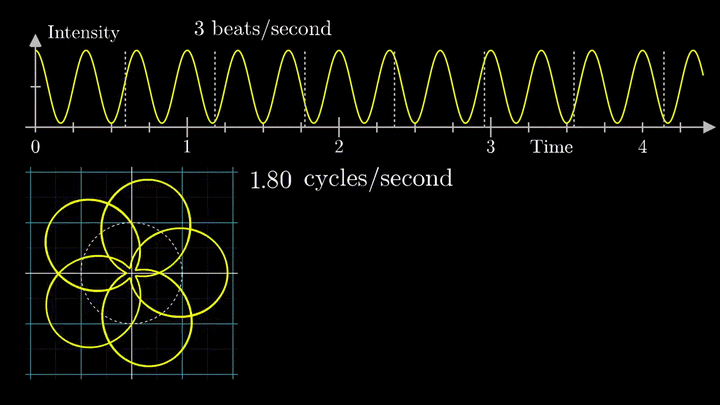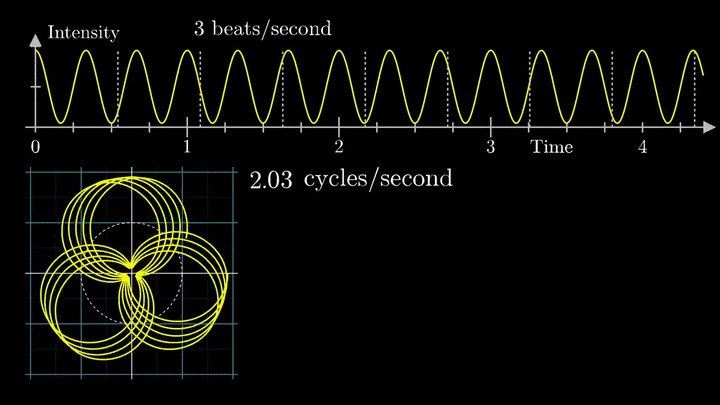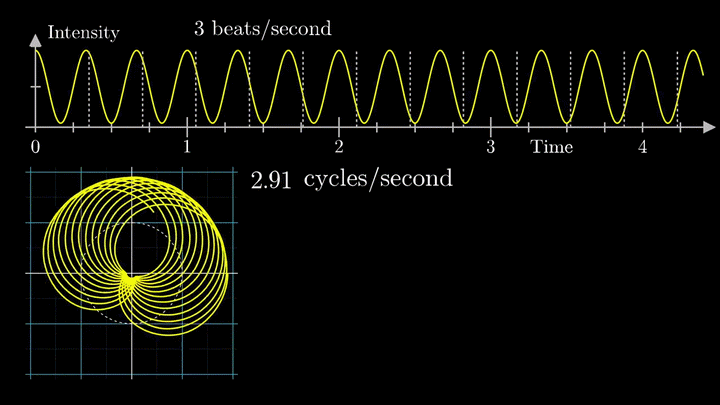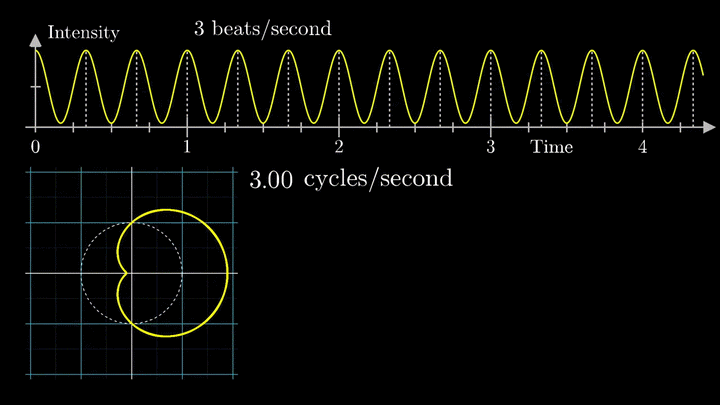
Наверное красивее всего это иллюстрирует одна программа, найденная мной на просторах сети. Выше уже говорилось, что график синуса является проекцией вращающегося вектора, а как же быть в случае более сложных сигналов? Это, как ни странно, проекция множества вращающихся векторов, а точнее их суммы, и выглядит это всё так:

Вектора рисуют пилу.
Вообще рекомендую сходить самим по ссылке и попробовать самим поиграться с параметрами, и посмотреть как меняется сигнал. ИМХО более наглядной игрушки для понимания я ещё не встречал.
Ещё следует заметить, что есть обратная процедура, позволяющая получить из данного сигнала частоту, амплитуду и начальную фазу (угол), которое называется Преобразование Фурье.

Разложение в ряд Фурье некоторых известных периодических функций (отсюда)
Я детально на нём останавливаться не буду, но покажу, как это можно применить по жизни. В списке литературы порекомендую то, где можно почитать подробнее о матчасти.
Переходим к практическим упражнениям!
Мне кажется, что каждый студент задаётся вопросом, сидя на лекции, например по матану: зачем мне весь этот бред? И как правило, не найдя ответа в обозримом будущем, к сожалению, теряет интерес к предмету. Поэтому я сразу покажу практическое применение данных знаний, а вы эти знания уже будете осваивать сами :).
Всё дальнейшее я буду реализовывать на сях. Делал всё, конечно, под Linux, но никакой специфики не использовал, по идее программа будет компилироваться и работать под другими платформами.
Для начала напишем программу для формирования звукового файла. Был взят wav-файл, как самый простой. Прочитать про его структуру можно тут.
Если кратко, то структура wav-файла описывается так: заголовок, который описывает формат файла, и далее идёт (в нашем случае) массив 16-ти битных данных (остроконечник) длиной: частота_дискретизации*t секунд или 44100*t штук.
Для формирования звукового файла был взят пример здесь. Я его немного модифицировал, исправил ошибки, и окончательная версия с моими правками теперь лежит на гитхабе тут
Сгенерируем двухсекундный звуковой файл с чистым синусом частотой 100 Гц. Для этого модифицируем программу таким образом:
Обращаю внимание, что формула чистого синуса соответствует той, о которой мы говорили выше. Амплитуда 32000 (можно было взять 32767) соответствует значению, которое может принимать 16-ти битное число (от минус 32767 до плюс 32767).
В результате получаем следующий файл (можно его даже послушать любой звуковоспроизводящей программой). Откроем данный файл audacity и увидим, что график сигнала в действительности соответствует чистому синусу:

Чистый ламповый синус
Поглядим спектр этого синуса (Анализ->Построить график спектра)

График спектра
Виден чистый пик на 100 Гц (логарифмический масштаб). Что такое спектр? Это амплитудно-частотная характеристика. Существует ещё фазочастотная характеристика. Если помните, выше я говорил, что для построения сигнала надо знать его частоту, амплитуду и фазу? Так вот, можно из сигнала получить эти параметры. В данном случае у нас график соответствий частот амплитуде, при чём амплитуда у нас не в реальных единицах, а в Децибелах.
Величина, выраженная в децибелах, численно равна десятичному логарифму безразмерного отношения физической величины к одноимённой физической величине, принимаемой за исходную, умноженному на десять.
В данном случае просто логарифм амплитуды, умноженный на 10. Логарифмический масштаб удобно использовать при работе с сигналами.
Мне, честно говоря, не очень нравится анализатор спектра в этой программе, поэтому я решил написать свой с блекджеком и шлюхами, тем более, что это несложно.
Пишем свой анализатор спектра
Здесь может быть скучно, поэтому можете перейти сразу к следующей главе.
Поскольку я прекрасно понимаю, что тут портянки кода размещать нет смысла, те, кому реально интересно — сами найдут и поковыряют, а тем, кому это неинтересно, будут скучать, то я остановлюсь только на основных моментах написания анализатора спектра wav-файла.
Во-первых, нам wav-файл необходимо читать. Там необходимо прочитать заголовок, чтобы понять, что содержит данный файл. Я не стал реализовывать море вариантов чтения данного файла, а остановился только на одном. Пример чтения файла был взят отсюда практически без изменений, ИМХО — отличный пример. Там же есть реализация на питоне.
Следующее, что нам нужно, это быстрое преобразование Фурье. Это то самое преобразование, которое позволяет получить из конечного набора точек вектора исходных сигналов. Пусть вас пока это не пугает, дальше я объясню.
Опять же, велосипед изобретать не стал, а взял готовый пример отсюда.
Я понимаю, что чтобы объяснить, как работает программа, надо объяснить, что такое быстрое преобразование Фурье, а это как минимум ещё на одну некислую статью.
Для начала алокируем массивы:
Скажу лишь, что в программе мы читаем данные в массив длиной size_array (которое берём из заголовка wav-файла).
Массив для быстрого преобразования Фурье должен представлять собой последовательность
Ряд Фурье
До сих пор мы говорили о движении струны. Однако звук, который представляет собой движение воздуха, вызванное движением струны, тоже должен состоять из тех же гармоник, хотя здесь мы уже не можем говорить о собственных гармониках воздуха. К тому же относительная сила различных гармоник в воздухе может быть совсем другой, чем в струне, особенно если струна «связана» с воздухом посредством «звучащей доски». Разные гармоники по-разному связаны с воздухом.
Если для музыкального тона функция f(t) представляет давление воздуха в зависимости от времени (скажем, такая, как на фиг. 50.1,6), то можно ожидать, что f(t) записывается в виде суммы некоторого числа простых гармонических функций от времени (подобных cos ωt) для каждой из различных гармонических частот. Если период колебаний равен Т, то основная угловая частота будет ω=2π/T, а следующие гармоники будут 2ω, Зω и т. д.
Здесь появляется небольшое усложнение. Мы не вправе ожидать, что для каждой частоты начальные фазы обязательно будут равны друг другу. Поэтому нужно пользоваться функциями типа cos (ωt + φ)- Вместо этого, однако, проще использовать для каждой частоты как синус, так и косинус. Напомним, что
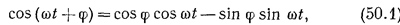 |
а поскольку φ — постоянная, то любые синусоидальные колебания с частотой со могут быть записаны в виде суммы членов, в один из которых входит sin ωt, а в другой — cos ωt.
Итак, мы приходим к заключению, что любая периодическая функция f(t) с периодом Т математически может быть записана в виде
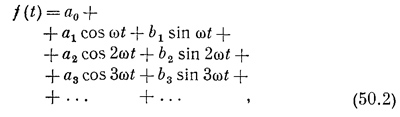 |
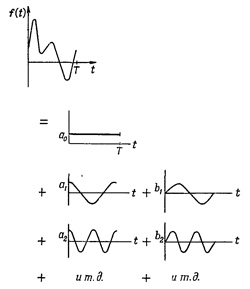
Мы сказали, что любую периодическую функцию можно написать в таком виде. Следует внести небольшую поправку и подчеркнуть, что в такой ряд можно разложить вообще любую звуковую волну или любую функцию, с которой мы сталкиваемся в физике. Математики, конечно, могут придумать такую функцию, что ее нельзя будет составить из простых гармонических (например, функцию, которая «заворачивает» назад, так что для некоторых величин t она имеет два значения!). Однако здесь нам не стоит беспокоиться о таких функциях.
Разложение колебаний в ряд Фурье. Гармонический спектр сложных колебаний



Колебания происходят вдоль одной прямой с разными частотами
Представим два складываемых колебания графически (см.рис 4).
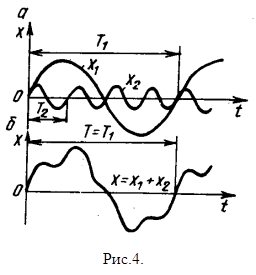 |
При сложении гармонических колебаний, происходящих с разными частотами w1 и w2 ( периодами Т1 и Т2) результирующее колебание не будет гармоническим, а будет представлять сложное периодическое движение. Если складываются гармонические колебания с кратными частотами (например, на рис.4 w2 = 4w1 ), то период результирующего колебания Т совпадает с периодом Т1 слагаемого наименьшей частоты: Т = Т1 или w = w1 .
Рассмотрение рис.4 приводит к утверждению, обратному сказанному выше и известному как теорема Фурье: любое сложное периодическое движение x(t) = x(t +T) c периодом Т можно представить в виде суммы простых составляющих гармонических колебаний (гармоник). Частоты этих гармоник кратны основной частотеw рассматриваемого периодического процесса.
Это утверждение можно записать в виде формулы, представляющей ряд Фурье:
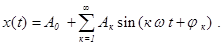
 |
Преобразование Фурье: самый подробный разбор
Преобразование Фурье – одно из базовых понятий в обработке сигналов и анализе данных. Но что оно означает? Геометрическая интерпретация.
Возьмём классическую задачу – работу со звуком. Теперь добавим конкретики.
Ваш друг приносит запись своего живого выступления. И это очень удачное выступление. Но! Хотя запись делали на хороший микрофон, в ней всё равно присутствует шум. Друг просит помочь убрать его или хотя бы уменьшить.
Здесь и пригодится знание преобразования Фурье.
Что такое звук в математическом смысле?
Отдельная нота – это гармонический сигнал с определённой частотой и амплитудой.
Как правило, мелодию, речь или иной звуковой сигнал можно представить как сумму гармонических сигналов. Шумом в таком случае мы называем слагаемые, соответствующие любым нежелательным звукам.
Преобразование Фурье позволяет разложить исходный сигнал на гармонические составляющие, что потребуется для выделения шумов.
Здесь g(t) – это исходный сигнал (в нашем случае запись друга). В контексте преобразования Фурье его называют оригиналом. G(f) – изображение по Фурье, а параметром f выступает частота.
Возможно, вам уже знакомо это определение. Но знаете ли вы, как происходит это преобразование? Если бы увидели его впервые, поняли бы, как с его помощью анализировать исходный сигнал?
Геометрическая интерпретация преобразования Фурье
Грант Сандерсон предлагает геометрический аналог преобразования Фурье. За несколько графических переходов от исходного сигнала к изображению каждая из компонент определения обретает смысл, а само преобразование получает новое геометрическое прочтение.
В дальнейшем обсуждении предполагается, что вы знакомы с векторами, интегрированием и понятием комплексного числа. Если каких-то знаний вам всё-таки не хватает, ознакомьтесь с материалами из нашей подборки по вузовской математике.
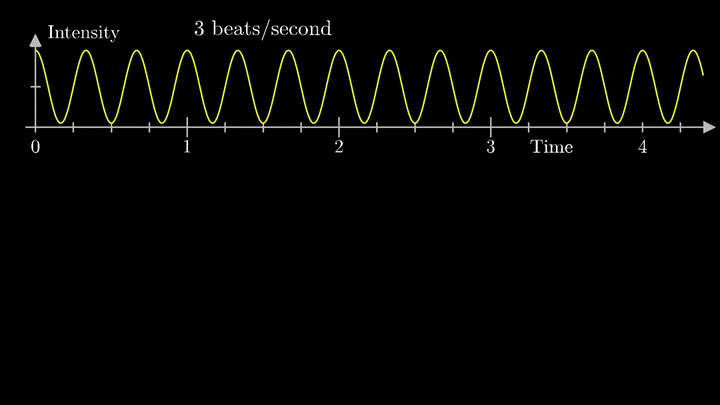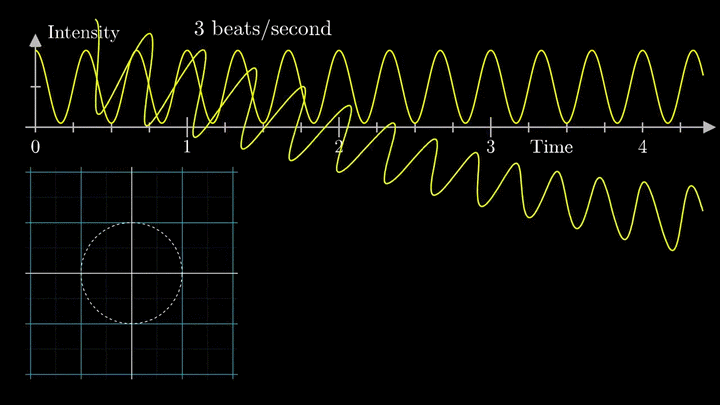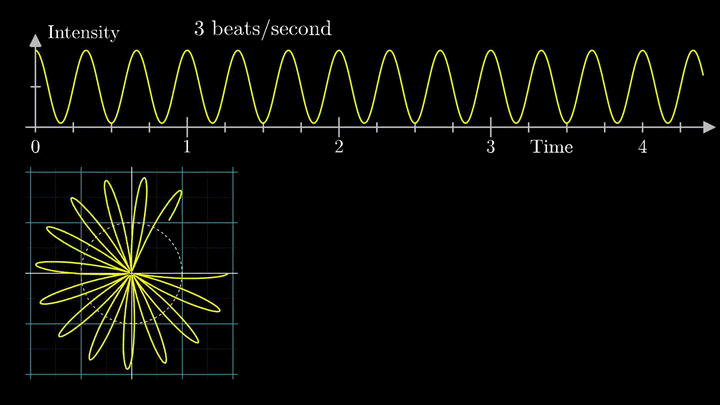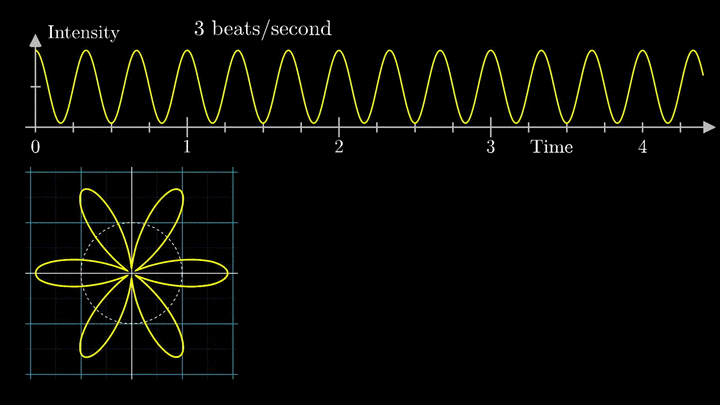
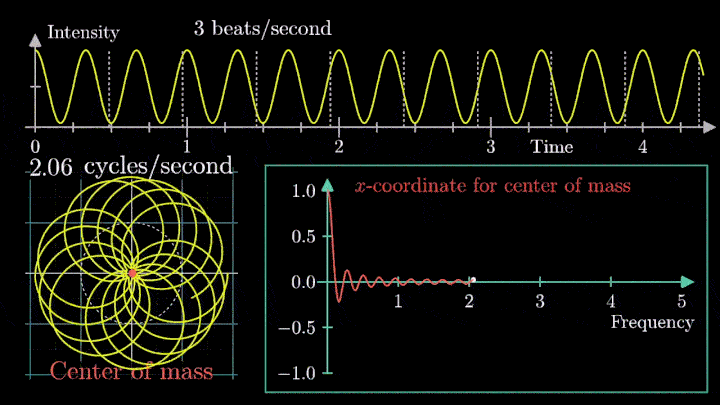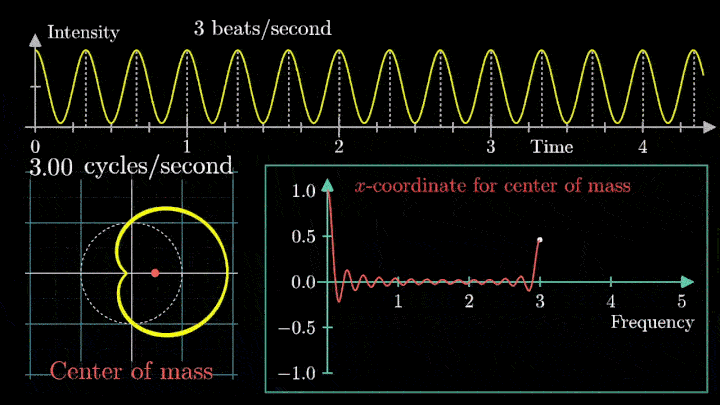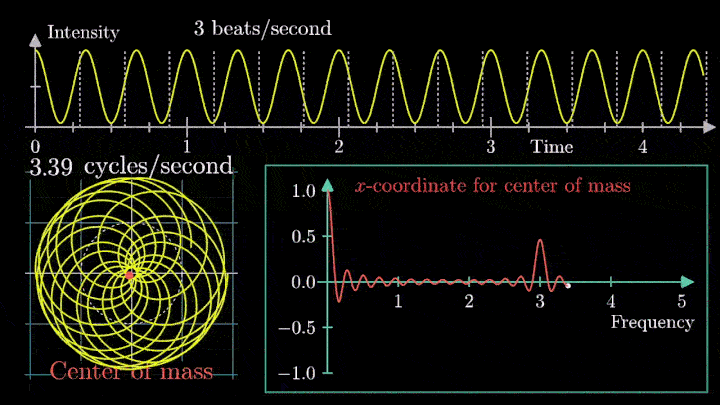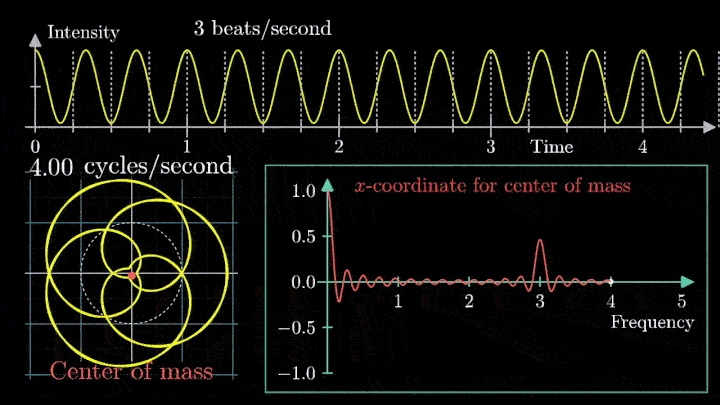
1. Наматываем сигнал
Отобразим g(t) на комплексную плоскость. Для этого введём радиус-вектор, который равномерно вращается по часовой стрелке. Его длина в каждый момент времени равна модулю значения сигнала, а частота вращения выбирается произвольным образом.
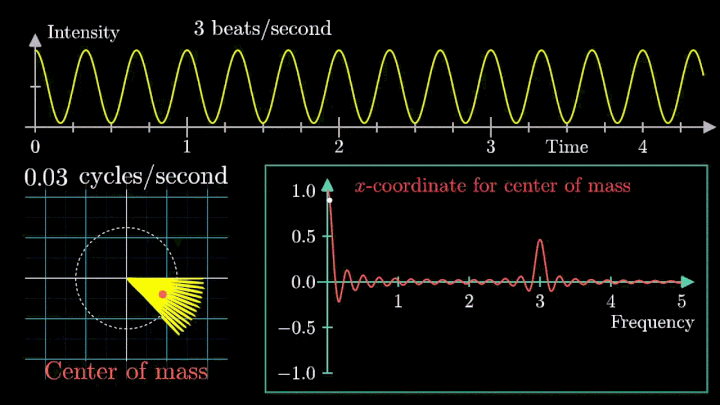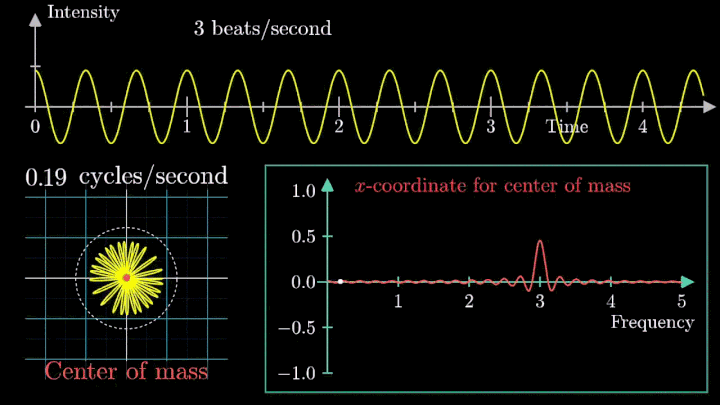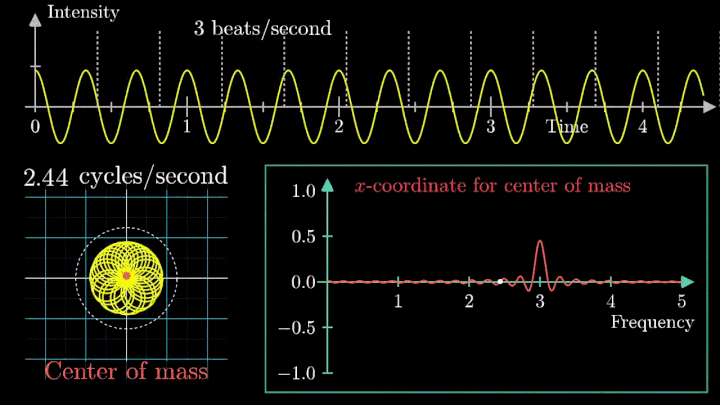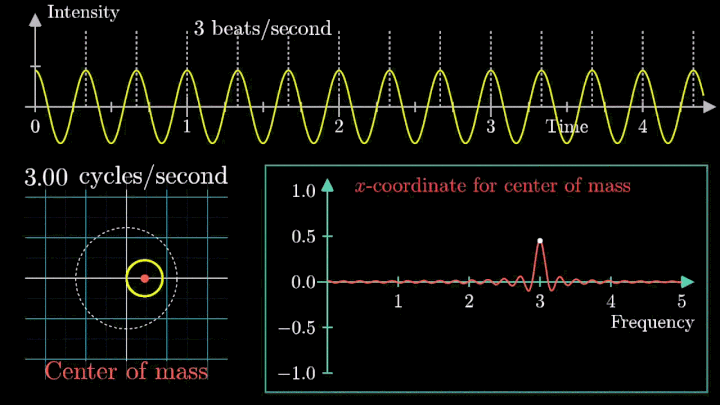
Теперь построим траекторию движения конца вектора, совершающего полный оборот за две секунды, или, другими словами, с частотой вращения fВ = 0.5 об/с.
Выглядит, будто мы намотали исходный сигнал на начало координат. В минимумах сигнала полученная «намотка» сливается с началом координат, а при приближении к максимумам – отклоняется.
Пока выглядит не особо информативно, не так ли?
А теперь увеличим частоты намотки.
Сначала график распределяется довольно симметрично относительно начала координат до частоты вращения fВ = 3 об/с. Затем максимумы резко смещаются в правую полуплоскость, а намотка перестаёт напоминать узор спирографа.
2. Ищем центр масс
Посмотрим внимательнее, что происходит. В качестве характеристики намотки возьмём усреднённое значение всех её точек – центр масс (отметим его оранжевым цветом).
Строим зависимость положения центра масс от частоты намотки. Сейчас нам достаточно рассмотреть х-кординату, но в дальнейшем для определения преобразования Фурье потребуются обе координаты.
Тогда что означает всплеск на низких частотах?
3. Анализируем влияние смещения
Возможно, вы обратили внимание, что рассматриваемый нами сигнал смещён на единицу. Сдвиг был введён для наглядности, но именно он приводит к усложнению поведения центра масс.
При нулевой частоте всё отображение сигнала на комплексной плоскости располагается на оси абсцисс. На малых частотах намотка по-прежнему группируется в правой полуплоскости.
Как только мы убираем сдвиг, т. е. берём сигнал вида g(t) = cos (6πt), намотка при низких частотах сдвигается влево по оси абсцисс.
Построение радиус-вектора остаётся аналогичным. Его длина равна модулю значения сигнала, направление вращения – положительное. Но при смене знака g(t) направление вектора меняется на противоположное.
Сейчас вы увидите, как меняется намотка и х-координата центра масс несмещённого сигнала.
Таким образом, на графике остался только один резкий скачок.
Это важный момент при использовании преобразования Фурье: линейный тренд и смещение проявляются на низких частотах, потому их исключают из исходного сигнала.
4. Выделяем частоты полигармонического сигнала
Мы наблюдаем два пика в точках fВ = 2 об/с и fВ = 3 об/с, что соответствует частотному составу исходной суммы.
Отметим ещё один интересный факт, верный как для х-координаты, так и для преобразования Фурье. Преобразование для суммы сигналов и сумма преобразований сигналов имеют один и тот же вид. Т. е. преобразование Фурье линейно.
Таким образом, этот подход позволяет определить частоту колебаний как моно-, так и полигармонического сигнала. Осталось математически описать процедуру вычисления центра масс намотки.
Вывод преобразования Фурье
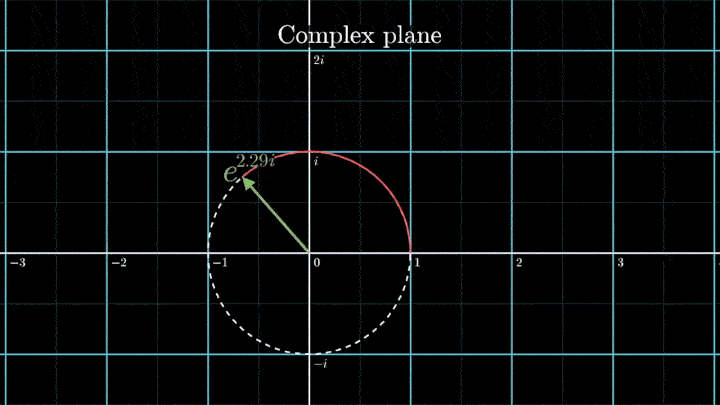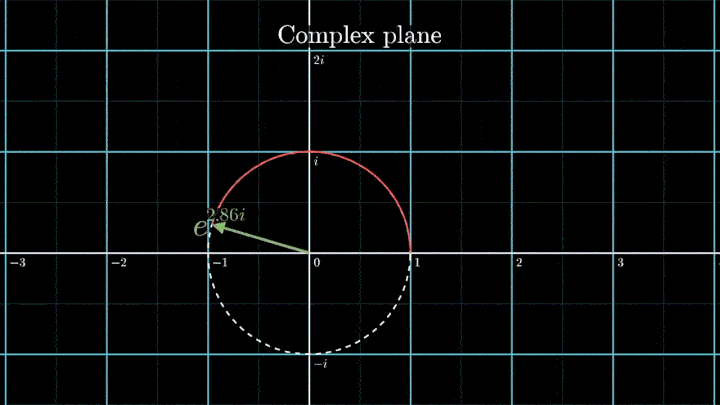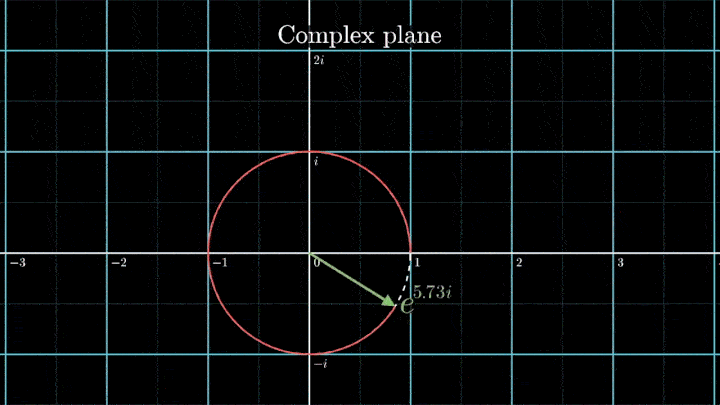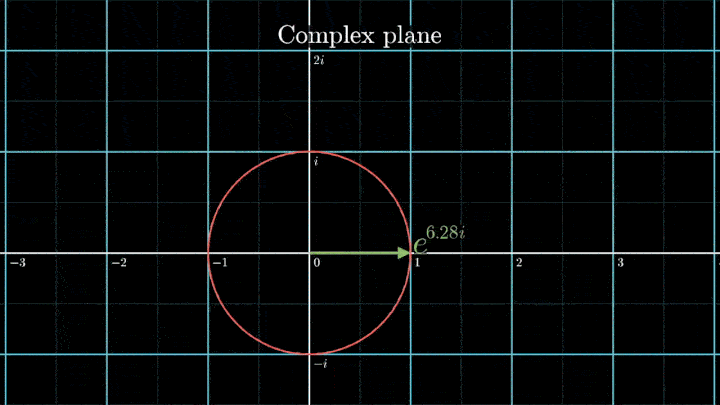
В самом начале рассмотрения мы отобразили исходный сигнал на комплексную плоскость. Такой выбор не случаен – это позволяет рассматривать точки на плоскости как комплексные числа и использовать формулу Эйлера для описания намотки:
Геометрически это соотношение означает, что при любом φ точка e iφ на комплексной плоскости лежит на единичной окружности.
Построим радиус-вектор e iφ при разных значениях φ.
При изменении φ на 2π вектор проходит полный оборот против часовой стрелки, так как 2π – длина единичной окружности. Чтобы задать скорость вращения вектора, показатель степени домножаем на ft, а для смены направления вращения – на -1.
Теперь вычисляем центр масс. Для этого отметим N произвольных точек на графике намотки и вычислим среднее:
Если мы будем увеличивать количество рассматриваемых точек, придём к предельному случаю:
где t1 и t2 – границы интервала, на котором рассматривается сигнал.
Выражение перед интегралом представляет собой масштабирующий коэффициент, но не отражает поведение центра масс. Потому его можно отбросить.
Полученное выражение и будет являться преобразованием Фурье с той разницей, что в общем виде интегрирование задаётся на интервале от -∞ до +∞.
Такой переход к бесконечному интервалу означает, что мы не накладываем никаких ограничений на длительность рассматриваемого сигнала.
Применение преобразования Фурье для фильтрации
Теперь, говоря о преобразовании Фурье, вы можете представлять его геометрическую интерпретацию – намотку сигнала на комплексную плоскость и вычисление центр масс.
При этом частота намотки f становится входным параметром для изображения по Фурье. Центр масс выступает оценкой, насколько хорошо соотносится (коррелирует) параметр f с присутствующими в сигнале частотами.
После того, как вы найдёте в принесённой другом записи все частотные компоненты, вам останется только вычесть их из изображения и применить обратное преобразование Фурье.
В гармонический ряд Фурье



Разложение периодических несинусоидальных функций
Общие определения
Часть 1. Теория линейных цепей (продолжение)
ЭЛЕКТРОТЕХНИКИ
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ
Учебное пособие для студентов электроэнергетических специальностей
Т. Электрические цепи периодического несинусоидального тока
Как известно, в электроэнергетике в качестве стандартной формы для токов и напряжений принята синусоидальная форма. Однако в реальных условиях формы кривых токов и напряжений могут в той или иной мере отличаться от синусоидальных. Искажения форм кривых этих функций у приемников приводят к дополнительным потерям энергии и снижению их коэффициента полезного действия. Синусоидальность формы кривой напряжения генератора является одним из показателей качества электрической энергии как товара.
Возможны следующие причины искажения формы кривых токов и напряжений в сложной цепи:
1) наличие в электрической цепи нелинейных элементов, параметры которых зависят от мгновенных значений тока и напряжения [R, L, C=f(u,i)], (например, выпрямительные устройства, электросварочные агрегаты и т. д.);
2) наличие в электрической цепи параметрических элементов, параметры которых изменяются во времени[R, L, C=f(t)];
3) источник электрической энергии (трехфазный генератор) в силу конструктивных особенностей не может обеспечить идеальную синусоидальную форму выходного напряжения;
4) влияние в комплексе перечисленных выше факторов.
Нелинейные и параметрические цепи рассматриваются в отдельных главах курса ТОЭ. В настоящей главе исследуется поведение линейных электрических цепей при воздействии на них источников энергии с несинусоидальной формой кривой.
Из курса математики известно, что любая периодическая функция времени f(t), удовлетворяющая условиям Дирихле, может быть представлена гармоническим рядом Фурье:
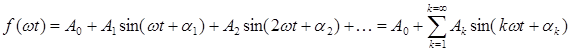
Амплитуды отдельных гармоник Ак не зависят от способа разложения функции f(t) в ряд Фурье, в то же время начальные фазы отдельных гармоник 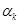
Отдельные гармоники ряда Фурье можно представить в виде суммы синусной и косинусной составляющих:
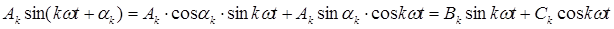
Тогда весь ряд Фурье получит вид:
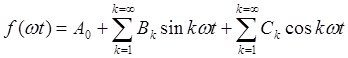
Соотношения между коэффициентами двух форм ряда Фурье имеют вид:
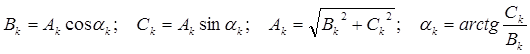
Если k-ю гармонику и ее синусную и косинусную составляющие заменить комплексными числами, то соотношение между коэффициентами ряда Фурье можно представить в комплексной форме:
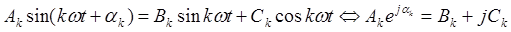
Если периодическая несинусоидальная функция времени задана (или может быть выражена) аналитически в виде математического уравнения, то коэффициенты ряда Фурье определяются по формулам, известным из курса математики:
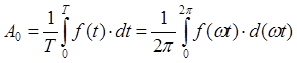
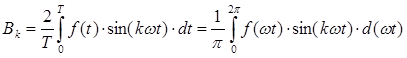
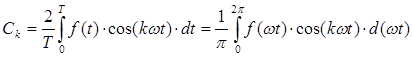
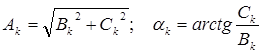
На практике исследуемая несинусоидальная функция f(t) обычно задается в виде графической диаграммы (графически) (рис. 118) или в виде таблицы координат точек (таблично) в интервале одного периода (табл. 1). Чтобы выполнить гармонический анализ такой функции по приведенным выше уравнениям, ее необходимо предварительно заменить математическим выражением. Замена функции, заданной графически или таблично математическим уравнением, получила название аппроксимации функции.