Что такое геометрическая фигура в пространстве

Содержание:

Предметом изучения геометрии являются свойства плоских и пространственных фигур.

Что такое геометрическая фигура

Что такое геометрическая фигура? В окружающем мире существует множество различных материальных предметов: жилые дома, детали машин, украшения из дерева и металла, природные минералы и т. д. Геометрия изучает не физические свойства этих предметов (например, цвет, массу, материал, из которого сделан предмет, и т. д.), а их форму и взаимное расположение.

Отвлекаясь от физических свойств предмета, мы приходим к АBСтрактному понятию геометрической фигуры, которая представляет собой любое множество точек.

Например, страница книги дает представление о геометрической фигуре, которая называется прямоугольником; комната имеет форму прямоугольного параллелепипеда; гробницы египетских фараонов построены в виде пирамид. Другими словами, различные предметы окружающего нас мира представляют собой физические модели геометрических фигур, а геометрические фигуры являются мысленными образами, к которым мы приходим, если принимаем во внимание только форму и размеры предметов.

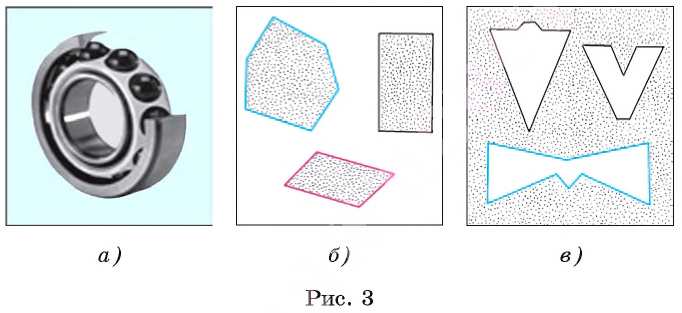
Апельсин и шарик в шарикоподшипнике (рис. 3, а) дают представление о шаре, а теннисный шарик и футбольный мяч являются физическими моделями геометрической фигуры, которая называется сферой (поверхность шара).

Простейшими (основными) геометрическими фигурами являются точка, прямая и плоскость. Мыслится, что у точки нет никаких размеров, прямая не имеет толщины и ширины, простирается неограниченно в обе стороны, а плоскость не имеет толщины, представляется идеально ровной, гладкой и неограниченной во всех направлениях.

Туго натянутая нить дает представление о части прямой, а гладкая поверхность письменного стола или оконного стекла — о части плоскости. Примерами геометрических фигур, которые называются многоугольниками, служат, например, фигуры, изображенные на рисунке 3, б, в.

Многообразие геометрических фигур очень велико. Любые известные геометрические фигуры могут служить основой для конструирования новых фигур.

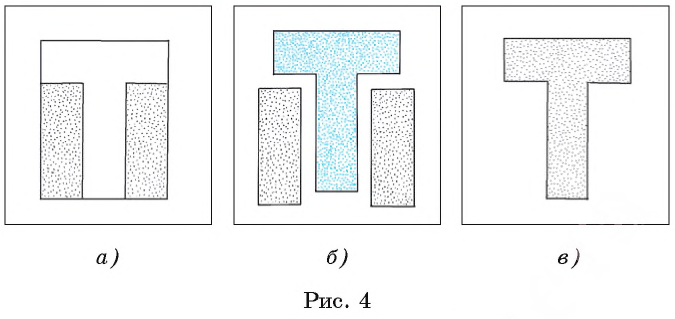
Например, если от прямоугольного листа бумаги отрезать две равные части, имеющие форму прямоугольника, как показано на рисунке 4, а, б, то мы получим модель геометрической фигуры, напоминающей букву «Т» (рис. 4, в).

Если есть несколько плоских фигур, то из них с помощью объединения или пересечения можно получить другие фигуры.

Объединение нескольких фигур — это фигура, которая состоит из всех точек данных фигур.

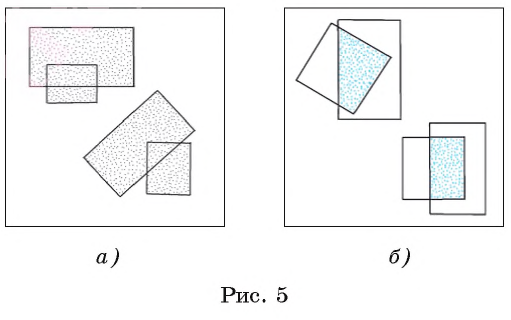
Например, на рисунке 5, а изображены фигуры, каждая из которых представляет собой объединение двух прямоугольников.

Пересечение нескольких фигур — это фигура, состоящая из всех общих точек данных фигур.

Например, на рисунке 5, B изображены четырехугольник и прямоугольник, которые являются пересечением прямоугольника и квадрата.

Пространственные фигуры

Плоские геометрические фигуры могут быть использованы также для конструирования различных пространственных фигур.

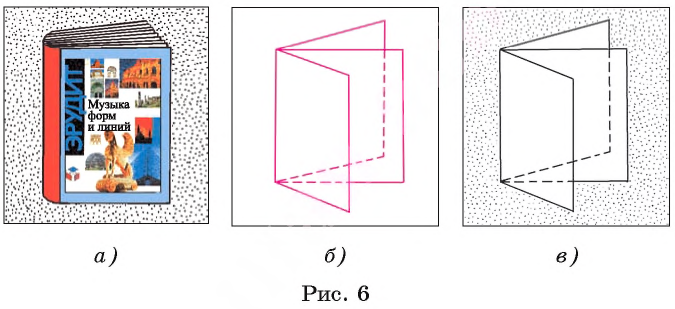
Например, страницы книги представляют собой модели прямоугольников (рис. 6, а). На рисунке 6, б, в изображена пространственная фигура, образованная тремя прямоугольниками с одной общей стороной.

Рассмотрим другие примеры моделей пространственных фигур.

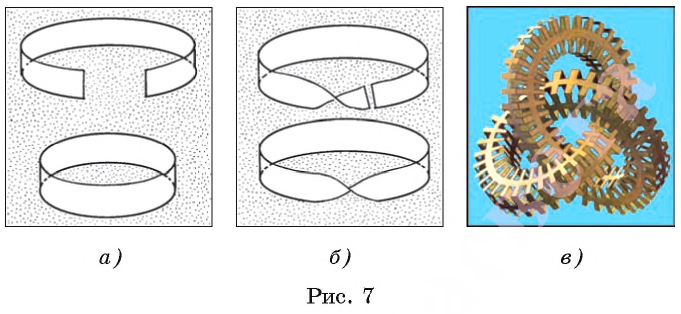
Пусть из листа бумаги вырезана узкая полоска, имеющая форму прямоугольника. Склеим меньшие края этой полоски, как показано на рисунке 7, а. Тогда мы получим модель пространственной геометрической фигуры, которая изображена на рисунке 7, а.

Если же указанную полоску предварительно «перекрутить» (это более удобно сделать, если полоска достаточно длинная и узкая), а затем склеить ее меньшие края, то получим модель пространственной фигуры, которая называется листом Мёбиуса (рис. 7, б). Мотивы указанной поверхности нашли художественное воплощение в графике голландского художника М. К. Эшера (рис. 7, в).

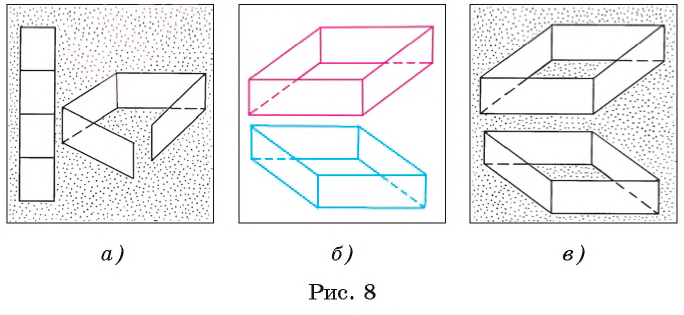
Рассмотрим еще один пример. Прямоугольную полоску бумаги разделим на четыре равные части, имеющие форму прямоугольника (рис. 8, а). Перегнем полоску по отрезкам, разделяющим ее на части, и склеим меньшие края (см. рис. 8, а). После склеивания мы получим модель пространственной геометрической фигуры, которая изображена на рисунке 8, б, в.

Другими примерами пространственных фигур являются геометрические тела. Наглядное представление о геометрическом теле дает часть пространства, которую занимает какое-либо физическое тело.

Примером еще одной пространственной фигуры, с которой вы уже знакомы, является прямоугольный параллелепипед. Поверхность прямоугольного параллелепипеда образована шестью прямоугольниками, которые называются его гранями. Ребрами прямоугольного параллелепипеда называются стороны прямоугольников, а их вершины — вершинами прямоугольного параллелепипеда.

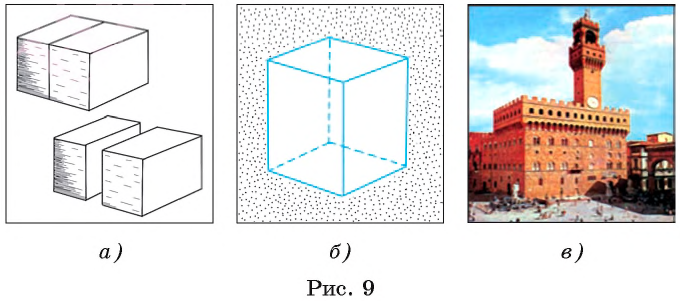
Представление о форме прямоугольного параллелепипеда дают модели, которые получаются при распиливании модели куба, например, сделанной из дерева, на две части, как показано на рисунке 9, а. Каждая из этих частей представляет собой модель прямоугольного параллелепипеда, который изображен на рисунке 9, б. Элементы многих архитектурных сооружений имеют форму параллелепипеда (рис. 9, в).

Заметим, что куб служит примером прямоугольного параллелепипеда, у которого все грани — квадраты.

Куб и прямоугольный параллелепипед — примеры геометрических фигур, называемых многогранниками.

Многогранники представляют собой наиболее простые геометрические тела в пространстве, аналогично тому, как многоугольники — наиболее простые фигуры на плоскости. С геометрической точки зрения многогранники — это часть пространства, ограниченная некоторым числом многоугольников — гранями многогранника. Стороны и вершины граней называются ребрами и вершинами многогранника. Грани многогранника образуют пространственную фигуру, которая называется поверхностью многогранника. Таким образом, например, прямоугольный параллелепипед можно рассматривать как часть пространства, ограниченную шестью прямоугольниками. Этот многогранник представляет собой пространственную фигуру, аналогичную прямоугольнику на плоскости.

Реальные объекты, имеющие форму различных многогранников, довольно разнообразны. Например, форму прямоугольного параллелепипеда имеют спичечный коробок, книга, комната, многоэтажный дом с горизонтальной крышей.

Фантазия и творчество помогут вам сконструировать модели многогранников более сложной формы.

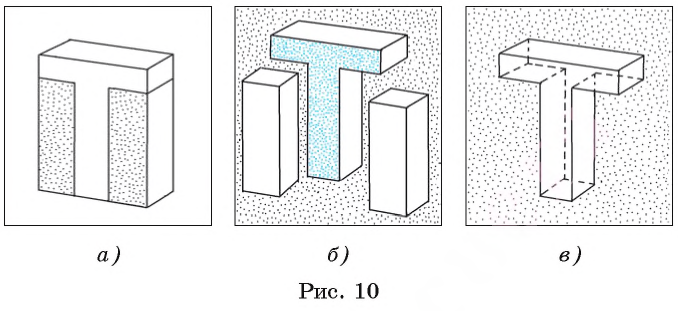
Например, если от деревянного бруска, имеющего форму прямоугольного параллелепипеда, отпилить два меньших брусочка, каждый из которых имеет форму прямоугольного параллелепипеда (рис. 10, а, б), то в результате получится модель многогранника, изображенного на рисунке 10, в.

Прямая призма

Количество примеров многогранников очень велико. Некоторые из многогранников имеют специальное название, например, выделяются многогранники, которые называются прямыми гс-угольными призмами.

Прямая n-угольная призма — это многогранник, поверхность которого образована многоугольниками, два из которых — равные между собой n-угольники (основания призмы), а остальные n граней являются прямоугольниками (боковые грани).

Ребрами прямой n-угольной призмы называются стороны прямоугольников, а их вершины называются вершинами прямой призмы.

Другими словами можно сказать, что прямая n-угольная призма — это часть пространства, ограниченная двумя равными n-угольниками и n прямоугольниками. Примерами предметов, имеющих форму прямой призмы, служат, например, ограненные карандаш, шляпка болта, гайка и др.

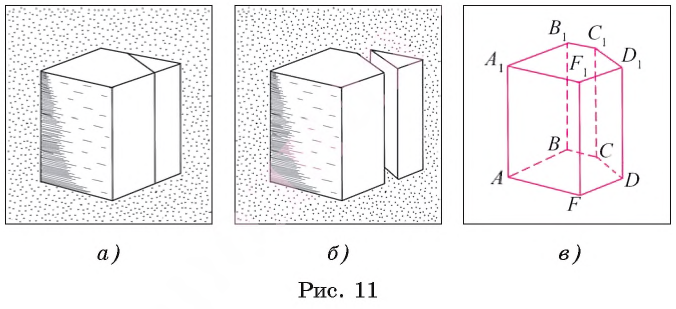
Представление о форме прямой призмы дают, например, модели, которые получаются в результате распиливания деревянного бруска, имеющего форму прямоугольного параллелепипеда, вдоль ребра, как показано на рисунке 11, а.

При этом получаются две модели, одна из которых представляет собой модель прямой пятиугольной призмы, а другая — модель прямой треугольной призмы (рис. 11, б).

Прямоугольный параллелепипед — пример прямой четырехугольной призмы, основаниями которой являются прямоугольники.

Разные виды производственной деятельности человека связаны с использованием моделей геометрических фигур.

Например, многие детали, которые используются в машиностроительном или мебельном производстве, имеют форму геометрических фигур, в частности некоторых многогранников.

человека на мысль о том, что теневой силуэт может передавать характерные признаки предмета и в определенной степени заменить оригинал. Художник эпохи Возрождения Леонардо да Винчи отмечал, что «первая картина состояла из одной линии, которая окружала тень человека, отброшенную солнцем на стену». Леонардо да Винчи был не только художником, но и математиком, механиком и инженером. В трактате «О многообразии» (1505) ученый изложил геометрический материал, необходимый в скульптуре, зодчестве и строительном искусстве.

Итальянские художники и архитекторы внесли особый вклад в создание теории изображений. Ими была разработана теория перспективы, позволяющая строить изображения, создающие наиболее полную иллюзию окружающей действительности.

Геометрия и искусство тесно связаны уже на самом раннем этапе становления человеческого мышления. Использование геометрических закономерностей в архитектуре и живописи было началом пути, на котором одновременно происходило зарождение искусства и геометрических представлений. Взаимопроникновение геометрии и искусства — один из механизмов интеллектуального развития человека и его творческих способностей, что подтверждается многочисленными примерами произведений искусства, созданными творцами прекрасного в процессе развития цивилизации.

Изображение фигур

В процессе изучения свойств геометрических фигур в качестве иллюстраций рассматриваются их различные изображения (графические модели) в тетради или на плоскости доски, что позволяет изучать геометрию более наглядно и доступно.

При изображении плоских фигур остаются неизменными их форма, величины углов, параллельность отрезков, отношение длин параллельных отрезков и отрезков, лежащих на одной прямой.

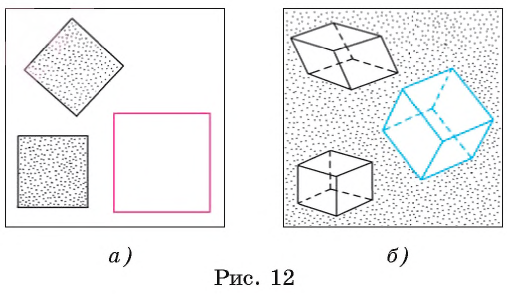
Например, при изучении свойств квадрата можно рассматривать любое изображение из тех, которые даны на рисунке 12, а.

Изображать пространственные фигуры несколько сложнее. Например, если мы рассмотрим модель куба, выполненную из дерева, то увидим, что все ребра куба равны между собой, а все грани представляют собой равные квадраты. На рисунке же некоторые грани куба изображаются параллелограммами и не все отрезки, изображающие ребра куба, имеют равные длины (рис. 12, б). Прямые углы рассматриваемой модели изображаются разными углами, а невидимые ребра нарисованы штриховой линией.

Такие правила изображения пространственных фигур являются оправданными. Действительно, заметим, что тень листа бумаги, имеющего форму квадрата, в зависимости от его расположения относительно солнечных лучей, имеет различную форму. В одних случаях тень имеет форму прямоугольника, в других — параллелограмма. Если, например, на модель куба, одна из граней которого параллельна поверхности стола, солнечные лучи будут падать строго вертикально, то тень указанной грани, которая получается на поверхности стола, будет иметь форму квадрата.

Грани куба — это квадраты, лежащие в разных плоскостях, расположенных в пространстве, одни грани мы изображаем в виде квадратов, другие — в виде параллелограммов, что позволяет получить представление о кубе.

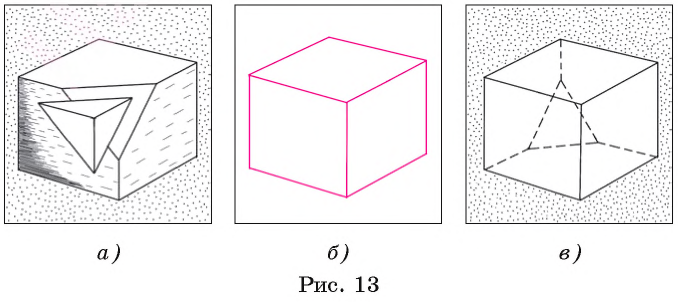
Для более полного представления о пространственных фигурах некоторые отрезки фигур изображаются штриховой линией. Подкрепим необходимость изображения некоторых отрезков штриховой линией следующим примером. Представим, что от модели куба, выполненной из дерева, отпилен уголок, как изображено на рисунке 13, а.

Предположим, что полученная после отпиливания уголка часть модели куба расположена так, что срез нам не виден. Если невидимые ребра полученной модели не нарисованы штриховыми линиями, то изображение, данное на рисунке 13, б, не дает полного представления о фигуре (например, можно предположить, что это есть изображение куба или фигуры, образованной тремя параллелограммами). Нарисовав невидимые отрезки штриховыми линиями (рис. 13, в), мы получим достоверное представление о форме фигуры (всей фигуры, а не только о видимой части).

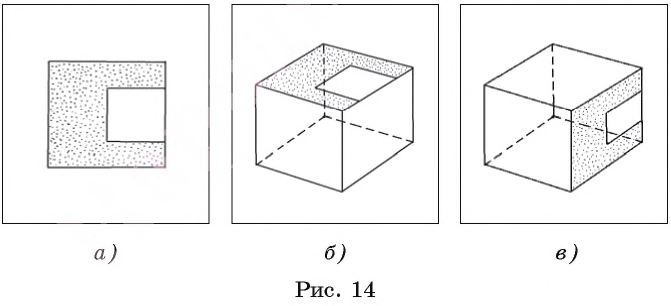
Подчеркнем, что изображение фигуры зависит от ее расположения в пространстве. Например, пусть дана фигура (часть квадрата), изображенная на рисунке 14, а. Если она является частью грани куба, тогда она может быть изображена, как показано на рисунке 14, б, в.

В процессе изучения геометрии в школе при изображении геометрических фигур, расположенных в пространстве, учитывается, что на изображениях фигур сохраняется параллельность отрезков, а также отношение длин параллельных отрезков и длин отрезков, на которые точка разбивает отрезок.

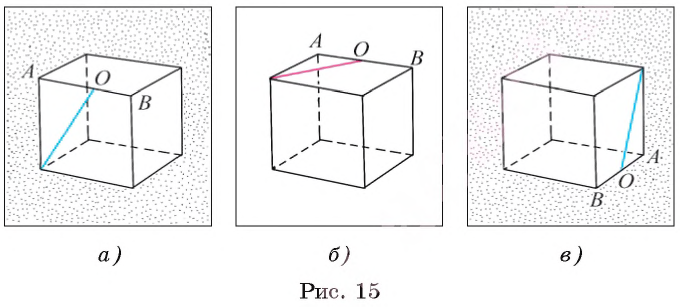
Например, если точка O является серединой ребра АВ куба, то при любом изображении куба точка O есть середина отрезка, изображающего ребро куба (рис. 15, а, б, в).

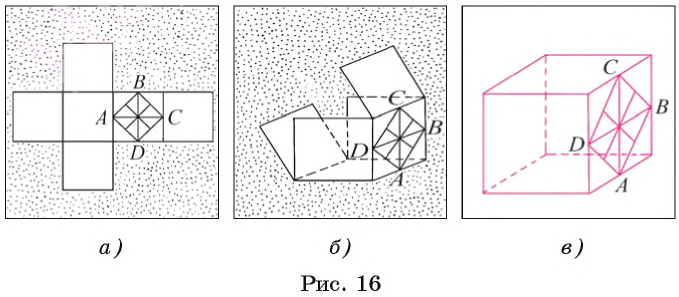
Рассмотрим еще один пример. Пусть на рисунке 16, а изображена развертка куба, а точки А, В, С, D) — середины соответствующих сторон квадрата. Тогда на изображении куба, поверхность которого можно «склеить» (рис. 16, б), пользуясь данной разверткой, точки А, В, С, D являются серединами соответствующих ребер куба (рис. 16, в).

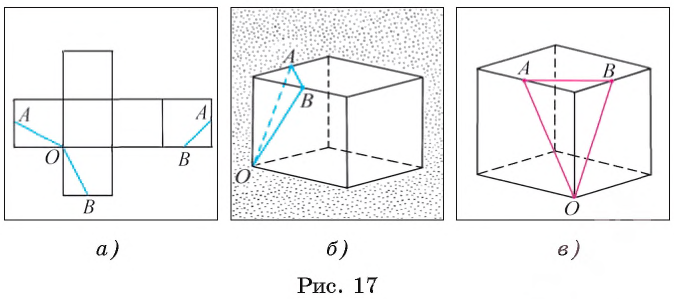
Пусть на развертке куба указаны отрезки ОА, ОВ и АВ, где точки А и В — середины сторон соответствующих квадратов (рис. 17, а). Тогда соответствующие отрезки на гранях куба будут изображаться так, как показано на рисунке 17, б, причем точки А и В — середины отрезков, изображающих ребра куба.

Заметим, что при одном изображении куба (рис. 17, б) отрезок ОА изображается штриховой линией. При другом изображении куба все три отрезка могут изображаться сплошной линией (рис. 17, в).

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Геометрические фигуры в пространстве

С пространственными геометрическими фигурами (куб, шар, параллелепипед и др.) дети знакомятся в практической деятельнос­ти (при конструировании, во время игры) гораздо раньше, чем с плоскими фигурами. Особенности мышления младших дошкольни­ков определяют выбор наглядного материала. В этом возрасте важ­но, чтобы изучаемый объект был крупный, яркий, чтобы им можно было выполнять действия (поиграть). Обследование идет на сенсор­ной основе, поэтому с моделями объемных фигур детям знакомить­ся легче. Кубики, шарики, бруски и др. входят в игру детей одно­временно с первыми игрушками. Обычно математические названия им не даются, но идет знакомство с различными объемными фор­мами, а в речь вводятся только некоторые термины.

Основными фигурами в пространстве считаются: точка, прямая, плоскость. На каждой плоскости выполняются все утверждения планиметрии. В стереометрии, так же как в планиметрии, вводится ряд аксиом, которые изучаются в школьном курсе геометрии.

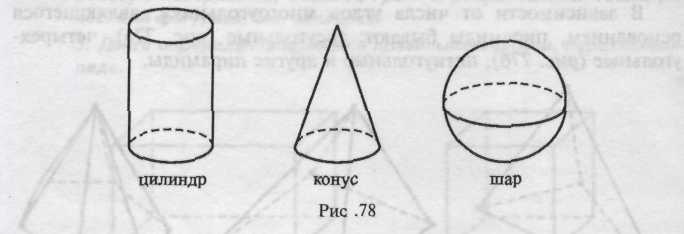
Объемные геометрические фигуры называют геометрическими телами. В пространстве выделяют многогранники (призма, пирамида и др.) и тела вращения (шар, конус, цилиндр и др.).

Многогранники

Многогранник называется выпуклым, если он расположен по одну сторону от плоскости любой его грани (рис. 70).

Выпуклый многогранник невыпуклый многогранник

Задание 43

Покажите вершины, ребра и грани многогранников, изображен­ных на рисунке 70. Какими геометрическими фигурами они явля­ются!

Задание 44

1. Вспомните, какие фигуры называют равными.

2. Назовите известные вам правильные выпуклые многогранники.

Всего существует 5 правильных многогранников, в отличие от правильных многоугольников, которых бесконечно много. Это об­условлено двумя причинами:

Куб — это прямоугольный параллелепипед с равными ребрами (или все грани которого являются квадратами) (рис. 76).

Дошкольники, изучая куб, могут отметить, что его поверхность состоит из шести квадратов, что у него 8 вершин. Свойства куба осваиваются ими, например, при выполнении такого задания: «Обклей кубик цветной бумагой. Что для этого нужно?» (вырезать 6 одинаковых квадратов).

Прямоугольный параллелепипед в детском саду часто называют «кирпичиком» или «бруском», что допустимо в предматематической подготовке. Эти слова являются предэталонными названиями гео­метрических фигур, так же как «кубик», «крыша» (треугольная при­зма), «столбик» (цилиндр) и др.

Младшим школьникам можно предложить задание: «Вырежи выкройку для коробки. Какую форму имеет каждая часть?» Таким образом, дети выясняют, что гранями прямоугольного параллелепи­педа являются прямоугольники, не формулируя этого явно.

Пирамида — многогранник, состоящий из плоского многоугольника (основания), точки, не лежащей в плоскости основания (вершины), и всех отрезков, соединяющих вершину пирамиды с точками основания (рис. 77). Отрезки, соединяющие вершину пирамиды с вершинами основания, называются боковыми ребрами. Поверхность пирамиды состоит из основания и боковых граней. Все боковые граны — треугольники.

В зависимости от числа углов многоугольника, являющегося основанием, пирамиды бывают: треугольные (рис. 77а), четырех­угольные (рис. 776), пятиугольные и другие пирамиды.

Любая грань треугольной пирамиды может служить ее основани­ем. Это же название носит и правильный многогранник, тетраэдр, гранями которого являются равные равносторонние треугольники.

Форму тетраэдра имеет пакет молока (старой упаковки), а еги­петские пирамиды имеют форму четырехугольной правильной пи­рамиды. Дошкольники называют «пирамидкой» совсем другую мо­дель — игрушку из колец разной величины, которая имеет форму конуса. Эта ситуация может вызвать затруднения в запоминании и правильном применении геометрических терминов у детей. Данная проблема преодолевается при своевременном грамотном объясне­нии и разделении названий игрушек от названий их формы, этало­нами для определения которой служат геометрические фигуры.

Задание 47

1. Нарисуйте пятиугольную пирамиду. Покажите ее основание, бо­ковую поверхность, боковые грани и ребра. Какими геометриче­скими фигурами они являются?

2. Дайте определения высоты пирамиды и правильной пирамиды.

Тела вращения

Изучая форму окружающих предметов, дошкольники сталкива­ются с телами вращения (рис. 78).

Эти фигуры называются телами вращения, так как они могут быть получены путем вращения некоторых плоских геометрических фигур.

Конус — это тело вращения, которое может быть получено путем вращения прямоугольного треугольника вокруг одного из его кате­тов, как оси (рис. 80),

Шар — это тело вращения, которое может быть получено путем вращения половины круга вокруг его диаметра, как оси (рис. 81).

Определения этих фигур из курса геометрии средней школы:

переносом, и всех отрезков, соединяющих

соответствующие точки этих кругов.

Шар— тело, которое состоит из всех точек пространства, нахо­дящихся на расстоянии не более заданного (радиуса) от данной точ­ки (центра).

Задание 48

— высоты цилиндре и прямого цилиндра;

— образующей конуса, высоты конуса и прямого конуса.

Обследование поверхности дает знание того, что основанием цилиндра и конуса является круг. Рисование объемных предметов разной формы на плоскости учит детей сравнивать, проводить ана­логию, моделировать, трансформировать пространство на плоскос­ти. Например, в процессе обсуждения таких вопросов: «Какой фор­мы мяч? Какую фигуру надо нарисовать, чтобы изобразить мяч?»

Знакомство с объемными фигурами расширяет знания детей об окружающем мире, закладывает основы для изучения геометрии в школе, обогащает их речь, формирует навыки обследования, раз­вивает мышление.

Вопросы для самоконтроля к теме № 3

1. Что изучает геометрия?

2. Что изучает планиметрия?

3. Что изучает стереометрия?

4. Что называется геометрической фигурой?

5. Назовите правила построения геометрии.

6. Назовите основные фигуры на плоскости и в пространстве.

7. Какие фигуры называются плоскими?

8. Какие фигуры называются выпуклыми?

9. Дайте определение отрезка.

10. Дайте определение луча.

11. Дайте определение угла.

12. Какая линия называется ломаной?

13. Какая ломаная называется простой?

14. Дайте определение многоугольника.

15. Какой многоугольник называется выпуклым?

16. Какой многоугольник называется правильным?

17. Дайте определение треугольника.

ТЕМА 4

ВЕЛИЧИНЫ И ИХ ИЗМЕРЕНИЕ

Понятие величины

Задание 49

Приведите примеры различных величии, изучаемых в школе на уроках математики, физики, химии. Вспомните способы их изме­рения и единицы этих величин.

Величину рассматривают как обобщение свойств некоторых объектов и как индивидуальную характеристику свойства конкрет­ного объекта. Например, свойство предметов «иметь протяжен­ность» называется «длиной».

Разнородные величины выражают различные свойства объектов (один предмет может иметь массу, объем и др.).

Источник