Что такое геометрическая интерпретация множеств

Геометрическая интерпретация множества действительных чисел. Окрестность точки

Определение 1.11.

Прямая, на которой выбраны направление, начало отcчета точка O и масштаб, называется числовой осью. Между действительными числами и точками числовой оси существует взаимно-однозначное соответствие: числу m∈R соответствует на оси точка M с абсциссой m. И обратно, каждой точке M числовой оси соответствует число m∈R абсцисса этой точки. Точка M лежит справа от точки O, если m>0 слева от точки O, если m˂0 совпадает с точкой O, если m=0. Поэтому действительные числа часто называют точками, что позволяет геометрически изображать числовые промежутки на числовой оси.

Определение 1.12.

Любой интервал числовой оси, содержащий данную точку a, называют окрестностью этой точки и обозначают O(a). Если этот интервал симметричен относительно точки a и имеет длину 2ε, то его называют ε− окрестностью точки a и обозначают Oε(a). Очевидно, что любая точка x∈Oε(a) удовлетворяет неравенствам a−ε˂x˂a+ε.

Определение 1.13.

Правой (левой) δ− полуокрестностью точки a называют интервал a˂x˂a+δ (a−δ˂x˂a) и обозначают O+δ(a) (O+δ(a))

Определение 1.14.

Окрестность точки a без самой точки a называют проколотой окрестностью этой точки и обозначают O(a)\a.

Определение 1.15.

Определение 1.16.

Точка a называется внутренней точкой множества A, если существует окрестность этой точки, содержащая точки только этого множества и не содержащая точек, не принадлежащих множеству A. Точка a называется граничной точкой множества A, если любая ее окрестность содержит как точки, принадлежащие множеству A, так и точки, не принадлежащие множеству A.

Например, x=1 для полуинтервала [0,2) есть внутренняя точка, x=0, x=2 граничные точки, причем точка x=0 принадлежит данному полуинтервалу, а точка x=2 не принадлежит.

Источник

Понятие множества, геометрическая интерпретация числовых множеств на числовой прямой

МАТЕМАТИКА (ТЕОРИЯ)

Профиль – начальное образование)

Пояснительная записка

Данный УМК разработан длястудентов – заочников направления «Педагогическое образование» по профилю «Начальное образование». По учебному плану на изучение «Математики» выделено всего 14 аудиторных часов, в течение которых преподавателю необходимо ознакомить студентов с теоретическими основами курса математики начального образования.

Запланированных 4 часов лекционных занятий достаточно только для краткого ознакомления с задачами изучения курса, рекомендации списка учебной литературы.

В дополнение к существующей учебной литературе для подготовки учителя начального образования по математике автор разработанного УМК предлагает необходимый, на его взгляд, теоретический материал по дисциплине «Математика».

Предложенный курс разбит на темы, в процессе изложения содержания тем выделены отдельные пункты, не предполагается никаких почасовых ограничений, материал предназначен в основном, для самостоятельного изучения курса математики.

Понятие множества, геометрическая интерпретация числовых множеств на числовой прямой

Операции с числовыми множествами (объединение, пересечение, разность).

Декартово произведение множеств

ТЕМА II – ЭЛЕМЕНТЫ МАТЕМАТИЧЕКСОЙ ЛОГИКИ

1. Понятие высказывания, логической операции с высказываниями.

Операции отрицания, конъюнкции, дизъюнкции, импликации,

Эквиваленции.

Свойства логических операций.

Понятие предиката с одной переменной.

Операции отрицания, конъюнкции, дизъюнкции, импликации,

Эквиваленции

(а) Логической операции «отрицание высказываний» соответствует логическая связка «не». Если высказывание А – истинно (т.е. А=1), то, утверждая, что А ложно, получаем новое высказывание, отрицание А, обозначается . При этом, если А=1, то =0, если А=0, то =1. Отрицание высказывания часто строится при помощи слова «неверно».Например, пусть А:

«Санкт – Петербург расположен на Неве» (А=1), тогда : «неверно что Санкт – Петербург расположен на Неве», или «Санкт – Петербург не расположен на Неве» ( =0). Все значения заданных и полученных высказываний сводятся в одну таблицу, таблицу истинности, которая позволяет ввести формальное определение операции.

Опр.2. Отрицаниемвысказывания А называется новое высказывание (неверно, что А), истинность которого задается таблицей (табл 1)

А

Опр.3. Конъюнкцией двух высказываний А и В называется новое высказывание С=A B, полученное соединением этих высказываний посредством связки «и» ( ), истинность которого определяется таблицей (Табл 2):

А

В

A B

Таблица показывает, что конъюнкция истинна только тогда, когда истинны оба высказывания, в остальных случая конъюнкция ложна.

Пример 1. Пусть имеем два высказывания А и В.

А: 5 3, В=0, по таблице истинности дизъюнкция A B:

(2=3) (2>3) – ложна, как дизъюнкция двух ложных высказываний.

Опр.5.Импликациейдвух высказываний А и В называется новое высказывание С=(A B), полученное соединением этих высказываний посредством связки «если…то» ( ), истинность которого определяется таблицей (Табл 4)

A

B

A B

Таблица показывает, что импликацияистинна всегда, кроме значения 0 в строке в которой имеется число 100.

Символическая запись «A В» читается:

Замечание 2: В обыденной жизни под выражением «если А, то В» обычно подразумевается тот факт, что если произойдет событие А, то произойдет и событие В. В математической логике это не всегда так. Для двух высказываний А (А: 10:5=2) и В (В: на улице холодно) можно построить импликацию «A В» (если 10:5=2, то на улице холодно). Истинность таких импликаций проверяется по таблицам истинности, однако с точки зрения здравого смысла такая импликация не имеет смысла.

Замечание 3: в изучении логических законов при введении для рассмотрения нового объекта А часто используется выражение «для любого А», для краткости это выражение записывается символически « А». Смысл этого символа рассмотрим позже.

Рассмотрим случай применения понятия импликации в курсе математики.

Пусть А: «Четырехугольник MNPQ – параллелограмм»

В: «Диагонали четырехугольника MNPQ в точке пересечения делятся пополам».

Импликация A В: «Если четырехугольник MNPQ параллелограмм, то его диагонали в точке пересечения делятся пополам».

Если А=1 и В=1, то (A В)=1 – получили известную теорему из курса геометрии основной школы.

С помощью таблиц истинности можно доказать логические формулы:

1.

2.

(д) Логической операции «эквиваленция» соответствует логическая связка «равносильно», «равнозначно», ее символ , A B – обозначение эквиваленции высказываний А и В.

Опр.6. Эквиваленциейдвух высказываний А и В называется новое высказывание С=(A B), полученное соединением этих высказываний посредством связки «равносильно» ( ), истинность которого определяется таблицей (Табл 5)

A

B

A B

Таблица показывает, что эквиваленция истинна тогда, когда оба высказывания имеют одинаковые значения истинности. Выражение A B читается:

— А тогда и только тогда, когда В.

Пример 1.

1). Выберем объекты исследования:

Множество натуральных чисел: N=

Множество множеств: М= < >

2). Введем операции с элементами в каждом множестве:

Сложение натуральных чисел: a+b

Объединение множеств: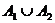

3). Введенные операции во множествах M и N обладают свойствами:

4). Введем отношения в множествах N и M:

Равенство натуральных чисел: а=b

Равносильность множеств:

5). Введенные отношения во множествах M и N обладают свойствами:

1) a=а – рефлексивности отношения равенства; 2) (а=b) (b=a) – симметричности отношения равенства; 3) — транзитивности отношения равенства.

1) — рефлексивности отношения равносильности; 2) — симметричности отношения равносильности; 3) — транзитивности отношения равносильности.

Рассмотренный пример показывает, насколько сходны свойства некоторых операций и некоторых отношений во множествах различной природы. Такого рода свойства отношений, структуру связей математических объектов ученые абстрагируют и изучают.

ТЕМА V – ОСНОВНЫЕ ПОНЯТИЯ ПОЗИЦИОННОЙ СИСТЕМЫ СЧИСЛЕНИЯ

Признак делимости.

1. Выберем два числа: , разложим число «а» по основаниям системы счисления – числа 10: (1) и будем искать условие, при котором .

1) Разделим на число «b» каждую из разрядных единиц числа «а»: :

— — неполные частные;

— — остатки от деления степеней 10 на число «b».

2) Подставим результаты деления в соотношение (1):

3) Обозначим S= — это сумма произведений чисел, обозначаемых цифрами числа «а», на остатки от деления соответствующих степеней 10 на число «b».

4) , число делится на число «b», поэтому «а» разделится на число «b», если на «b» разделится число «S».

1. Понятие функции одной переменной.

2. Свойства функции y=f(x.

3. Прямая пропорциональная зависимость величин.

ТЕМА VIII – ОСНОВНЫЕ ПОНЯТИЯ УРАВНЕНИЙ

Числовые выражения.

Числовые выражения

Опр.1. Математическим выражением называется последовательность букв латинского алфавита, чисел, знаков действий и скобок. Например, .

Если выражение состоит только из чисел, то выражение называется числовым, если выражение содержит буквы, то оно называется выражением с переменными. Например, -выражение числовое, -выражение с двумя переменными. Значением числового выражения называется число, полученное в результате последовательного выполнения операций, указанных в выражении. Например, значение выражения равно , а значения выражения не существует, так как на нуль делить нельзя.

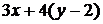
Значениями переменной называются числа, которые можно подставить в выражение вместо переменной. Множество таких чисел называется областью определения выражения. Например, в выражение вместо можно подставлять любые числа ; в выражение любые числа , кроме , так как при этом в знаменателе получаем число нуль.

Пусть -два числовых выражения. Соединим их знаками равенства (=) или неравенства (>, 0 такое, что — свойство инвариантности (неизменности).

Длина отрезка как величина

Пусть задано некоторое множество отрезков S=<a,b,c,…m>, Введем в этом множестве отношение , означающее равенство отрезков a=b, выражение означает, что отрезок «а» состоит из отрезков «b» и «с». обозначим через некоторое положительное действительное число, назовем его мерой отрезка «а».

Опр. 3. Число называется длиной отрезка , если для можно поставить в соответствие некоторое число так, чтобы выполнялись условия:

(1) = );

(2) ; (свойство аддитивности);

(3) — существует единичный отрезок «е», которому сопоставляется число единица;

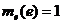
(4) если для отрезков множества S существуют два единичных отрезка «е» и «f», то можно найти такое число , что (свойство инвариантности).

Например, е=1см, f=1м, и пусть см, м, тогда , т.е. к=0,01.

Из предыдущего имеем следствия:

1) — при замене единичного отрезка «е» на равный ему единичный отрезок «f» длина отрезка не изменится.

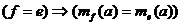
2) — если меры отрезков одинаковы, то отрезки измерены одним и тем же единичным отрезком.

МАТЕМАТИКА (ТЕОРИЯ)

Профиль – начальное образование)

Пояснительная записка

Данный УМК разработан длястудентов – заочников направления «Педагогическое образование» по профилю «Начальное образование». По учебному плану на изучение «Математики» выделено всего 14 аудиторных часов, в течение которых преподавателю необходимо ознакомить студентов с теоретическими основами курса математики начального образования.

Запланированных 4 часов лекционных занятий достаточно только для краткого ознакомления с задачами изучения курса, рекомендации списка учебной литературы.

В дополнение к существующей учебной литературе для подготовки учителя начального образования по математике автор разработанного УМК предлагает необходимый, на его взгляд, теоретический материал по дисциплине «Математика».

Предложенный курс разбит на темы, в процессе изложения содержания тем выделены отдельные пункты, не предполагается никаких почасовых ограничений, материал предназначен в основном, для самостоятельного изучения курса математики.

Понятие множества, геометрическая интерпретация числовых множеств на числовой прямой

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

Источник