Что такое геоцентрическая система координат
Геоцентрические координаты и точность их определения
Введение. Главным предметом данной статьи, в первую очередь, является повторение материала, относящегося к разделу «Системы координат». В основе своей, материал затронет ряд важнейших, для повторения, определений и тезисов, а также будет рассмотрен ряд вопросов, касательно интересующей нас темы. Дополнением, к основным определениям и выдержкам, станет краткое описание влияния методик определения геоцентрических координат и точностей данных определений.
Одной из задач прикладной геодезии является определение положения предметов и характерных точек на местности. В качестве метода, для их определения, служат системы координат. Система координат (СК) – совокупность определений, использующих способ описания положения точки с помощью чисел – координат. Координаты – величины, описывающие местоположение точки на плоскости (для плоских систем координат) или в пространстве (для пространственных систем координат), в принятой СК. Исходя из такого широкого определения, следует, что существует огромное множество различных, по своей структуре и способу задания, систем отчета.
Рассмотрев вопрос решения обильного количества прикладных задач, логично сделать вывод о необходимости использования «удобных» систем отсчета, позволяющих, без лишних манипуляций, получить удовлетворительные и достоверные результаты, как расчётов, так и измерений.
Геоцентрическая система координат. Геоцентрическая система координат – представляет собой декартовую прямоугольную (прямолинейную) систему координат, определяющуюся точкой – началом координат, и базисом из трех векторов – осями координат.
Геоцентрические координаты, точность их определения. «Геоцентрические координаты – величины, определяющие положение точки в системе координат, у которой начало совпадает с центром масс Земли» ГОСТ 22268-76
Вопрос об источниках ошибок ГНСС измерений является довольно обширным, и его повторение является темой отдельной статьи. В свою очередь хотелось бы отметить, что в общих чертах, влияние данного параграфа не внесет существенных изменений в непосредственную тему доклада – точность определения геоцентрических координат.
(1) – При использовании грубого C\A кода
(2) – Статистический метод (Static Positioning)
(3) – Данные приведены для двухчастотных приемников.
Космическая (спутниковая) геодезия
Первые наблюдения за небесными телам начались еще в 17 веке с изобретением первых телескопов. С развитием приборостроения и появлением новых оптических приборов и отсчетных механизмов для них, повышалась точность измерений, что в свою очередь давало людям возможность лучше понимать размеры и форму Земли, а также других объектов нашей Солнечной системы и даже целой Вселенной.
Благодаря началу гонки вооружений и развитию космической отрасли был запущен первый искусственный спутник Земли в 1957 г. Что дало возможность проведения измерений на ИСЗ как на точку в небе с известными координатами. Тяга человека к освоению космоса привела к запуску еще большего количества спутников, которые уже можно было не только измерять с Земли методами классической геодезии, но и сами спутники проводили измерения между собой и Землей. Это привело к появлению новых методы измерений, и в десятки раз увеличилась точность измерений. Вскрылись глубокие и обширные связи геодезии (ее задач и проблем) с другими науками о космическом пространстве и о Земле. Таким образом формировался раздел геодезии, получивший название космическая геодезия.
Космическая геодезия — это научная дисциплина, в которой для решения научных и практических задач геодезии используются результаты наблюдений искусственных спутников Земли (ИСЗ), космических аппаратов (КА) и Луны и звёзд.
В соответствии с этим в предмет изучения в рамках космической геодезии входят:
• теории движения небесных тел;
• разработка способов определения орбит небесных тел (прямая задача) и вычисления эфемерид (обратная задача);
• обоснование требований к геодезическим спутникам в отношении параметров их орбит и состава бортовой аппаратуры;
• обоснование требований к расположению станций наблюдения и их аппаратурного оснащения;
• изучение методов наблюдений и теории математической обработки наблюдений;
• интерпретация результатов наблюдений и их обработки.
Задачи космической геодезии
Задачи космической геодезии тесно связаны с проблемами картографирования Земли из космоса, с различными видами съемок ее поверхности, что весьма важно для получения планетарных характеристик Земли и изучения ее природных ресурсов. Наблюдение далеких небесных тел и расчёт их эфемерид помогает в освоении космоса и запусках космических кораблей.
1. Основной задачей КГ является определение размеров и формы Земли. Вместе с другими величинами, такими как гравитационная постоянная Земли, скорость вращения они образуют набор, называемый фундаментальными параметрами Земли. Используя методы КГ, геодезисты определили фундаментальные параметры не только для Земли, но и для Луны, Марса, Венеры и Меркурия.
2. Создание геоцентрической системы координат, которая подходила бы ко всей Земле. Такие системы у нас принято называть общеземными.
3. Определение положения и изменения со временем координат наземных пунктов, а также изменение траектории ИСЗ. Летая над поверхностью Земли ИСЗ испытывает на себе влияние гравитационных аномалий, из-за чего изменяется траектория его движения. Отсюда следует, что если получать его орбиту в разные моменты времени, то можно по изменению в орбите определить гравитационные аномалии и по ним найти положение геоида (или квазигеоида) над эллипсоидом. По изменению положения наземных пунктов можно измерять и моделировать геодинамические явления (например, движение полюсов Земли, определение характеристик вращения Земли – точного времени, движений литосферных плит).
Возникновение и развитие космической геодезии
Чтобы лучше понять, почему возникла необходимость в развитии методов космической геодезии, следует остановиться на некоторых моментах из истории геодезии.
Известно, что различные геодезические работы выполнялись людьми с глубокой древности. Одними из первых известных нам геодезистов были египтяне. Они использовали для восстановления разрушаемых разливами Нила границ земельных угодий опорные пункты, которые находились вдали от реки. Также важное значение имело ориентирование и определение местоположения в сухопутных и морских путешествиях.
По мере развития человечества повышались требования к точности геодезических работ, совершенствовались методы и техника измерений, способы обработки измерительной информации.
Важное значение для развития геодезии имело предложение голландского ученого Снеллиуса (1580-1626 гг.) использовать в качестве метода передачи координат триангуляцию. В 1615-1617 гг. Снеллиус выполнил в Голландии градусное измерение по дуге меридиана, состоящее из 33 треугольников и имеющее протяженность около 130 км.
В XX веке для создания геодезического обоснования, наряду с триангуляцией, стала применяться полигонометрия. Ее развитие стимулировало широкое внедрение в геодезическое производство радио- и светодальномеров. Их использование позволило создавать геодезические построения методом трилатерации (путем измерения длин сторон треугольников).
Традиционные геодезические построения создавались на отдельных, разделенных значительными водными преградами или государственными границами, территориях. По ним были образованы геодезические референцные системы. К их числу относятся референц-эллипсоиды Бесселя, Кларка, Красовского, Хейфорда и др. (всего более 10). Положение референц-эллипсоидов, образующих геодезические системы на разных континентах, относительно друг друга и центра масс Земли нельзя установить при помощи только триангуляции и полигонометрии.
Ограниченные возможности классических методов в смысле передачи координат обусловлены сравнительно небольшими предельными длинами сторон триангуляции и полигонометрии (20-30 км), а также требованием взаимной видимости между пунктами. Для этого пункты строились на вершинах гор, а на равнинной местности устанавливались специальные сигналы.
В 1768 году Иоган Эйлер (сын Леонарда Эйлера) опубликовал работу, в которой обосновал возможность определения параметров земного эллипсоида по одновременным измерениям зенитных расстояний Луны с пунктов, расположенных на одном меридиане и имеющих известные астрономические координаты.
С начала XX века внимание к так называемым «лунным» методам усилилось, и космическая геодезия стала оформляться как раздел геодезической науки. Предпринимались попытки использовать для решения геодезических задач результаты наблюдений моментов покрытий звезд Луной, солнечных затмений и фотографирования Луны на фоне звезд. Из-за значительного удаления Луны от Земли (в среднем 384 000 км) лунные методы не позволяют достичь требуемой в настоящее время для решения геодезических задач точности. Например, применение фотографирования Луны на фоне звезд (наиболее точного из названных методов) обеспечивает получение координат пунктов наблюдений с ошибкой примерно 100 м.
В 1946 г. финский геодезист Ю. Вяйсяля разработал принципы построения триангуляции путем фотографирования вспышек света на фоне звезд. Для этого источник света поднимали на значительную высоту самолетом, газовым баллоном или ракетой и по команде с Земли он давал кратковременные вспышки. С двух пунктов на поверхности земли выполнялось синхронное фотографирование двух и более вспышек света в различных вертикальных плоскостях, по результатам которого можно было с высокой точностью определить направление хорды, соединяющей пункты наблюдений. Если таким образом определить направления хорд, соединяющих все пункты наблюдений, то можно вычислить координаты последних. Для этого необходимо знать координаты хотя бы одного из пунктов и длину хотя бы одной хорды.
Проводившиеся в ряде стран эксперименты по созданию таких построений показали, что при сторонах 100-300 км звездная триангуляция позволяет получать результаты достаточно высокой точности (ошибка направления хорды составляет 0,5-1,5²). Однако расстояния между пунктами были ограничены высотой баллонов с лампами-вспышками, которые могли подниматься на высоту до 30-40 км.
С запуском в СССР 4 октября 1957 г. первого в мире искусственного спутника Земли появилась возможность создавать космические построения, основанные на наблюдениях ИСЗ. Измерения доплеровского сдвига частоты передатчика этого спутника на пункте наблюдения с известными координатами позволили определить параметры движения ИСЗ. Обратная задача была очевидной: по измерениям одного и того же доплеровского сдвига при известных координатах ИСЗ найти координаты пункта наблюдения.
Все системы координат, применяемые в космической геодезии
При решении задач космической геодезии приходится использовать различные системы координат, отличающиеся между собой:
1. Расположением начала отсчета координат
• планетоцентрические
• геоцентрические
• квазигеоцентрические (референцные)
• планетографические
• топоцентрические
• спутникоцентрические
• барицентрические
2. Ориентацией основной плоскости
• экваториальные
• горизонтальные
• орбитальные
3. Ориентацией начальной плоскости
• гринвичские
• равноденственные
4. Видом координатных систем
• прямоугольные
• полярные
• цилиндрические
• сферические
• сфероидические
В настоящее время наиболее распространенными являются прямоугольные системы координат в трехмерном евклидовом пространстве, для задания которых необходимо указать начало, масштаб и ориентировку осей.
Среди многочисленных систем координат, используемых для решения тех или иных задач, выделим две основные — инерциальную (равноденственную) и общеземную.
Для практической реализации этих систем координат используется косвенный метод, то есть системы координат задаются совокупностью реперов (звёзды, квазары, точки земной поверхности), положение которых определяется из специальных наблюдений.
Инерциальная система координат
Геоцентрическая общеземная система координат
Орбитальная система координат
Орбитальная система координат состоит из плоскости орбиты, эксцентрическая аномалия Е, девиация D и радиальное расстояние r0. Девиация определяет угловое отклонение объекта в эпоху t от плоскости орбиты в начальную эпоху t0 из-за возмущений в его движении. Для перехода от орбитальной системы координат в прямоугольную необходимо знание элементов орбиты. Элементы орбиты характеризуют положение орбиты в пространстве, ее размер и форму, а также положение небесного тела на орбите.
Объектоцентрическая система координат
Под объектоцентрической системой координат понимается система, отнесенная к центру масс ИСЗ с осями, направленными по радиусу-вектору и к точкам юга и востока в плоскости местного горизонта. Одна ко для анализа точности вычисления положения ИСЗ и остаточных уклонений измеренных величин чаще используется система координат, оси которой направлены вдоль радиуса-вектора и перпендикулярно к нему по движению ИСЗ в плоскости и поперек орбиты так, чтобы система оказалась правой.
Геодезические системы координат
Горизонтальная система координат
Большинство измерений на земной поверхности выполняются в горизонтальной системе координат, связанной с отвесной линией. В данной работе горизонтальной системой координат будет считаться система, вертикальная ось которой направлена по нормали к поверхности эллипсоида, а горизонтальные оси – по касательным к меридиану и параллели в сторону возрастания широт и долгот. Эта система координат отличается от системы, связанной с отвесной линией, на величины составляющих уклонения отвесной линии, поэтому в наблюдения необходимо вводить соответствующие поправки.
Плоские прямоугольные системы координат
В практике геодезических и картографических работ, как правило, используются плоские системы координат. Они получаются при отображении эллипсоида на плоскости с помощью формул картографических проекций. Наиболее употребительными из них являются проекции Гаусса и Ламберта. Существуют также условные плоские системы координат, которые отличаются нестандартными началами или приближенно аппроксимируют некоторую условную систему.
Поэтому геоцентрические координаты пунктов, определенные относительным методом, необходимо перевычислить в требуемую плоскую систему координат.
Эти перевычисления ведутся в следующей последовательности:
Методы создания геоцентрической системы координат
Гравиметрический метод
Гравиметрический метод состоит в изучении различными способами гравитационного поля Земли и представлении его в виде разложения по сферическим функциям.
Способы изучения гравитационного поля земли:
• гравиметрический наземный
• астрономо-геодезическим
• спутниковым альтиметрическим
• градиентометрическим и др.
Астрономо-геодезический метод
Астрономо-геодезический метод впервые был доведен до практического применения в работе И.Д. Жонголовича, где уравнение поправок для большой полуоси и координат центра общеземного эллипсоида x0, y0, z0 относительно центра некоторого референц-эллипсоида
Рассматриваемый метод реализует следующую идею. Если достаточно точно определить фигуру квазигеоида и аппроксимировать ее эллипсоидом вращения при условии минимума отклонений фигуры квазигеоида от эллипсоида по методу наименьших квадратов, то этот эллипсоид и будет общеземным, а его центр будет совмещен с ЦМЗ. Но, как известно, результат такого решения зависит от точности и объема доступной гравиметрической информации. Использование этого метода в пределах некоторых стран и регионов привело к созданию множества референц эллипсоидов и национальных систем координат.
Метод разрабатывался в течение всего развития наземной геодезии, так как геодезисты всегда стремились изучать реальную физическую поверхность Земли, и только из-за ограниченности доступной измерительной информации получали референцную систему координат. В настоящее время опыт развития космической геодезии и нового уравнивания астрономо геодезической сети (АГС) СССР дает основания для уточнения некоторых постоянных, по уравнениям поправок градусных измерений предлагалось определить поправку к большой полуоси референц-эллипсоида Δа и координаты центра общеземного эллипсоида (ОЗЭ) Хо, Уо, Zo.
Речь должна идти о большем числе определяемых параметров.
При развитии геодезической сети на некоторой территории и обработке астрономо-геодезических данных предварительно принимается некоторый эллипсоид относимости, на который редуцируются все измерения. Его параметры ориентирования обычно задаются координатами исходного пункта, высотой геоида (квазигеоида) и исходным азимутом, которые, как правило, устанавливаются из астрономических определений. Для редукции измерений на эллипсоид относимости развиваются сети нивелирования и выполняется гравиметрическая съемка. Для исключения накопления ошибок измерений определяются пункты Лапласа с астрономическими координатами и азимутами, которые связаны не с эллипсоидом относимости, а с физической поверхностью Земли. На этом этапе предполагается, что это и есть ОЗЭ.
Спутниковые методы создания геоцентрической системы координат
Спутниковые методы создания геодезических сетей геометрический, орбитальный, динамический и навигационный, а также их сочетания и разновидности.
Например, метод коротких дуг является разновидностью орбитального метода. Геоцентрические системы координат создаются только орбитальным и динамическим методами.
При обработке любых наблюдений используется некоторая модель исследуемого объекта. Например, в наземных сетях совокупность координат исходных пунктов и предварительных координат определяемых является моделью создаваемой геодезической сети, которая затем оптимизируется методом наименьших квадратов под имеющиеся измерения.
В спутниковых сетях, кроме предварительных координат пунктов, используются модель сил, воздействующих на движение спутника, фундаментальные геодезические и геофизические постоянные и другие величины, совокупность которых составляет так называемую Стандартную Землю.
Отличие орбитального метода от динамического состоит в том, что в орбитальном методе модель движения ИСЗ и параметры ГПЗ считаются исходными, а определяемыми, кроме координат пунктов, являются только начальные условия орбитальных дуг. В динамическом методе, кроме неизвестных орбитального метода, определяются параметры ГПЗ. Однако это не означает, что в орбитальном методе не могут определяться некоторые дополнительные неизвестные (например, баллистический коэффициент или координаты полюса), а в динамическом методе нет никаких принятых за исходные величин. Деление на модельные и определяемые параметры весьма условно и главное отличие динамического и орбитального методов состоит все же в определении, прежде всего, параметров ГПЗ, но исходная модель Стандартной Земли в них одна и та же.
При создании КГС используется следующая общая технология :
— проектирование и создание космического геодезического комплекса;
— планирование и выполнение наблюдений ;
— предварительная обработка материалов наблюдений;
— интегрирование и предварительное уточнение начальных условий орбитальных дуг;
— общее орбитальное или динамическое решение;
— распространение полученных результатов на другие параметры Стандартной Земли и при необходимости повторение общего решения с уточнённой моделью Земли.
В проекте создания модели Стандартной Земли предусматривается проектная точность получения ее параметров, число намеченных к запуску геодезических ИСЗ, количество и расположение пунктов КГС, их оснащение измерительными средствами, длительность периода наблюдений, порядок и сроки обработки материалов и получения окончательных результатов.
После запуска ИСЗ и испытания функционирования бортовых систем в его управляющий процессор (БЦВМ) периодически закладывается программа работы бортовых систем, обеспечивающая включение и выключение бортовых передатчиков и другой аппаратуры в зонах видимости наблюдательных пунктов или при выходе из н их. Центральный пункт управления комплексом (ЦУП) осуществляет постоянный радиоконтроль орбиты ИСЗ, поэтому практически не возникает задачи предварительного определения параметров орбиты. Эфемериды ИСЗ могут быть рассчитаны на длительное время вперед и тем или иным способом доведены до наблюдателей.
Заключение
Космическая геодезия – это не только совокупность нетрадиционных космических методов, позволяющих решать научные и практические задачи геодезии как науки о Земле, ведь «гео» – это по-гречески (γ̃η) Земля! Космическая геодезия – это не только научная дисциплина, использующая естественные и искусственные космические объекты для решения геодезических задач. Мы стоим на пороге постановки и решения основной задачи космической геодезии (как самостоятельной научной дисциплины): создание единой координатной основы для работы в Солнечной системе. Это значит, что космическая геодезия, начав с глобального изучения Земли, как одной из планет, в перспективе поможет человечеству выйти на уровень освоения всей Солнечной системы.
Геоцентрические системы координат



Системы координат
Необходимость в использовании различных координатных систем в спутниковых технологиях обусловлена тем, что для вычисления орбит спутников и прогнозирования их движения применяются одни системы координат, а для определения пространственного положения точек требуются другие системы координат.
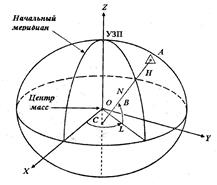
Системы, начало которых совпадает с центром масс Земли, называют геоцентрическими [34]. Земными (рис. 1) – называют системы, вращающиеся вместе с Землей и у которых:
— ось z проходит через условный земной полюс (УЗП);
— ось x проходит через точку G пересечения плоскостей экватора и начального меридиана;
— ось y дополняет систему до правой.
Рисунок 1. Геоцентрическая земная система координат
На рисунке 1 обозначено: О – начало координат, В – геодезическая широта, L – геодезическая долгота, Н – геодезическая высота, А – точка находящаяся на физической поверхности Земли, а – проекция точки А на поверхность эллипсоида, N = ac – радиус кривизны эллипсоида в плоскости первого вертикала.
В геодезии используют общеземную систему координат, которая должна отвечать следующим условиям:
— начало координат совмещается с центром масс Земли;
— масса эллипсоида должна равняться массе Земли;
— эллипсоид должен наиболее лучше описывать физическую поверхность Земли.
Для определения геодезических координат требуется знать параметры земного эллипсоида. Параметры некоторых общеземных эллипсоидов приведены в таблице 1.
Параметры для эллипсоидов WGS-84, ПЗ-90 и Красовского
| Название параметров | Разме-рность | Общеземные эллипсоиды | ||
| WGS-84 | ПЗ-90 | Красовского | ||
| Большая полуось α | м | 6 378 137 | 6 378 136 | 6 378 245 |
| Знаменатель сжатия, 1/α | б/р | 298.257223563 | 298.257839303 | 298.3 |
Для решения геодезических задач требуется так же знать и гравитационное поле Земли. А для того, чтобы осуществить пересчет из одной системы в другую, необходимо знать параметры преобразований.
Все геоцентрические системы связаны с определенными эллипсоидами, название которых обычно совпадают с названием самой системы. В этом случае возможно использование не только декартовых, но и эллипсоидальных координат: геодезическая широта B, геодезическая долгота L и геодезическая высота H (см. рисунок 1).
Система координат, виды и классификация
Пойдем прямым логическим путем, не отвлекаясь на многие современные международные и отечественные научные термины. Систему координат можно изобразить как некую систему отсчета ориентированную на плоскости двумя направлениями, а в пространстве тремя. Если вспомнить математическую систему, то она представлена двумя взаимно перпендикулярными направлениями, имеющими названия осей абсцисс (X) и ординат (Y). Ориентированы они в горизонтальном и вертикальном направлениях соответственно. Пересечение этих линий является началом координат с нулевыми значениями в абсолютной величине. А местоположение точек на плоскости определяется при помощи двух координат X и Y. В геодезии ориентирование осей на плоскости отличается от математики. Плоскостная прямоугольная система определена осью X в вертикальном положении (в направлении на север) и осью Y в горизонтальном (в направлении на восток).
Классификация систем координат
В геодезии все системы координат можно представить в виде двух групп:
В обеих группах выделяют как плоские (двухмерные), так и пространственные (трехмерные) системы.
К прямолинейным прямоугольным системам относятся цилиндрическая проекция Гаусса-Крюгера, индивидуальные референцные и местные системы координат.
К полярным системам можно отнести географическую, астрономическую и геодезическую, геоцентрические и топоцентрические системы.
Географическая система координат
Замкнутая поверхность внешнего контура Земли представлена сфероидной геометрической формой. За основные направления ориентирования на ней можно принять дуги на поверхности шара. На упрощенно представленном уменьшенном макете нашей планеты в виде глобуса (фигура земли) можно зрительно увидеть принятые линии отсчета в виде Гринвичского меридиана и экваториальной линии.
В этом примере выражена общепринятая во всем мире именно пространственная система географических координат. В ней введены понятия долготы и широты. Имея градусные единицы измерения, они представляют угловую величину. Многим знакомы их определения. Следует напомнить, что географическая долгота конкретной точки представляет угол между двумя плоскостями, проходящими через нулевой (Гринвичский) меридиан и меридиан в определяемой точке расположения. Под географической широтой точки принят угол, образующийся между отвесной линией (или нормалью) к ней и плоскостью экватора.
Понятия астрономической и геодезической системы координат и их различия
Географическая система условно объединяет астрономическую и геодезическую системы. Для того чтобы было понятно какие все-таки существуют различия обратите внимание на определения геодезических и астрономических координат (долготы, широты, высоты). В астрономической системе широта рассматривается как угол между экваториальной плоскостью и отвесной линией в точке определения. А сама форма Земли в ней рассматривается как условный геоид, математически приближенно приравненный к сфере. В геодезической системе широта образовывается нормалью к поверхности земного эллипсоида в конкретной точке и плоскостью экватора. Третьи координаты в этих системах дают окончательное представление в их различиях. Астрономическая (ортометрическая) высота представляет собой превышение по отвесной линии между фактической и точкой на поверхности уровенного геоида. Геодезической высотой считается расстояние по нормали от поверхности эллипсоида до точки вычисления.
Система плоских прямоугольных систем координат Гаусса-Крюгера
Каждая система координат имеет свое теоретическое научное и практическое экономическое применение, как в глобальном, так и региональном масштабах. В некоторых конкретных случаях возможно использование референцных, местных и условных систем координат, но которые через математические расчеты и вычисления все равно могут быть объединены между собой.
Геодезическая прямоугольная плоская система координат является проекцией отдельных шестиградусных зон эллипсоида. Вписав эту фигуру внутрь горизонтально расположенного цилиндра, каждая зона отдельно проецируется на внутреннюю цилиндрическую поверхность. Зоны такого сфероида ограничиваются меридианами с шагом в шесть градусов. При развертывании на плоскости получается проекция, которая имеет название в честь немецких ученых её разработавших Гаусса-Крюгера. В таком способе проецирования углы между любыми направлениями сохраняют свои величины. Поэтому иногда ее называют еще равноугольной. Ось абсцисс в зоне проходит по центру, через условный осевой меридиан (ось X), а ось ординат по линии экватора (ось Y). Длины линий вдоль осевого меридиана передается без искажений, а вдоль экваториальной линии с искажениями к краям зоны.
Полярная система координат
Кроме выше описанной прямоугольной системы координат следует отметить наличие и использование в решении геодезических задач плоской полярной системы координат. За исходное отсчетное направление в ней применяется ось северного (полярного) направления, откуда и название. Для определения местоположения точек на плоскости используют полярный (дирекционный) угол и радиус-вектор (горизонтальное проложение) до точки. Напомним, что дирекционным углом считается угол, отсчитываемый от исходного (северного) направления до определяемого. Радиус-вектор выражается в определении горизонтального проложения. К пространственной полярной системе добавляется геодезические измерения вертикального угла и наклонного расстояния для определения 3D-положения точек. Этот способ практически ежедневно применяется в тригонометрическом нивелировании, топографической съемке и для развития геодезических сетей.
Геоцентрические и топоцентрические системы координат
По такому же полярному методу частично устроены и спутниковые геоцентрическая и топоцентрическая системы координат, с той лишь разницей, что основные оси трехмерного пространства (X, Y, Z) имеют отличные начала и направления. В геоцентрической системе началом координат является центр масс Земли. Ось X имеет направление по Гринвичскому меридиану к экватору. Ось Y располагают в прямоугольном положении на восток от X. Ось Z изначально имеет полярное направление по малой оси эллипсоида. Координатами в ней считаются:
При наблюдении за движением спутников из точки стояния на земной поверхности используют топоцентрическую систему, оси координат которой расположены параллельно осям геоцентрической системы, а ее началом считается пункт наблюдения. Координаты в такой системе:
В современные спутниковые глобальные системы отсчета WGS-84, ПЗ-90 входят не только координаты, но и другие параметры и характеристики важные для геодезических измерений, наблюдений и навигации. К ним относятся геодезические и другие константы: