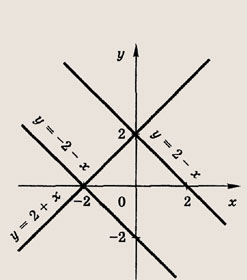
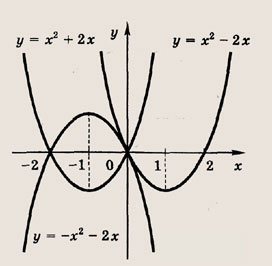
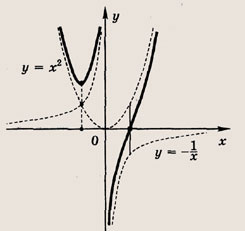
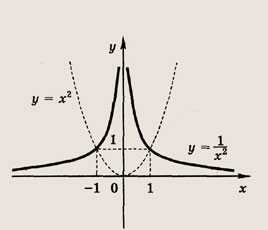
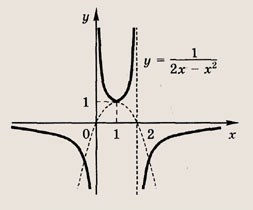
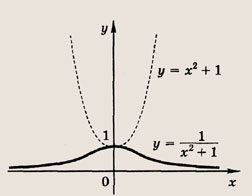
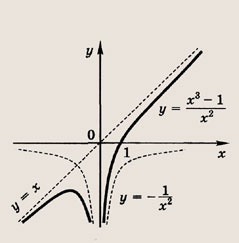
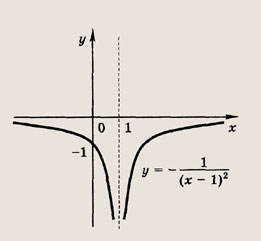
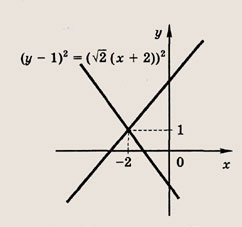
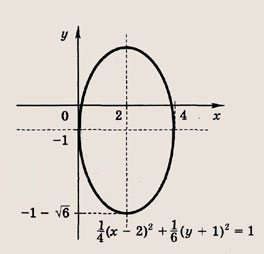
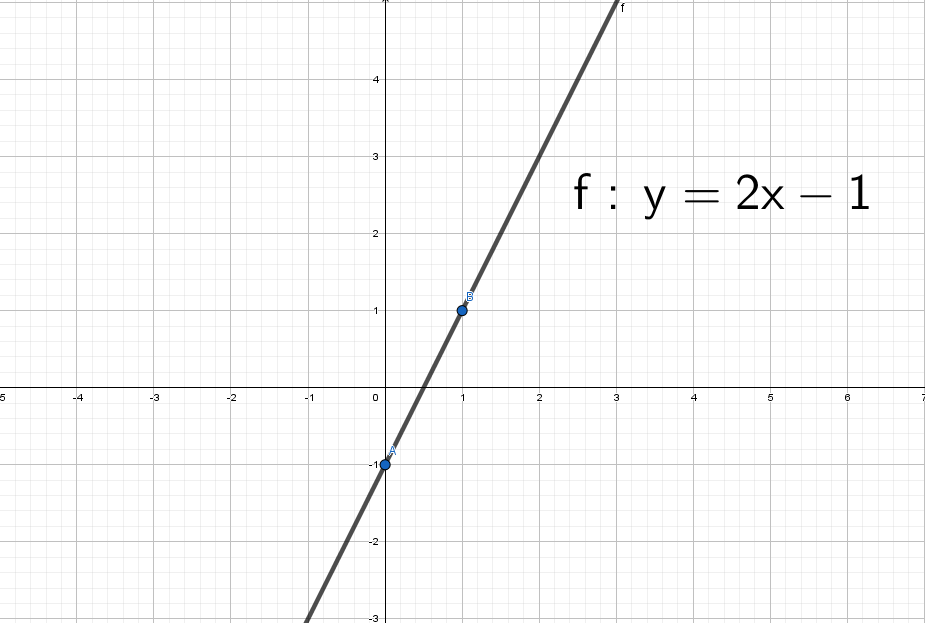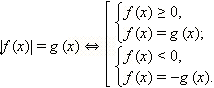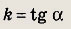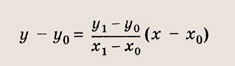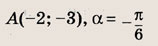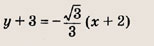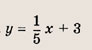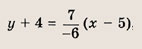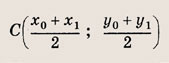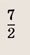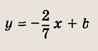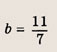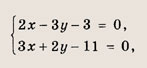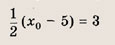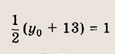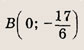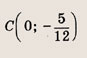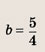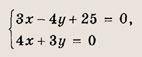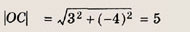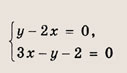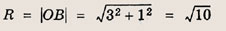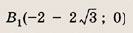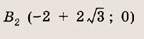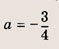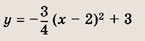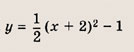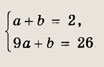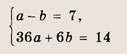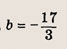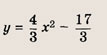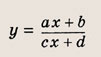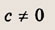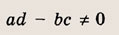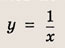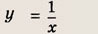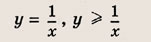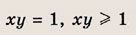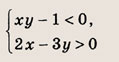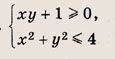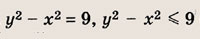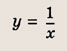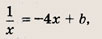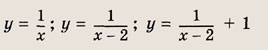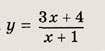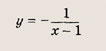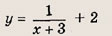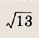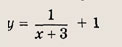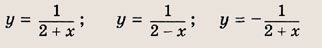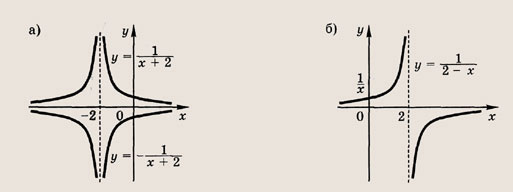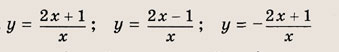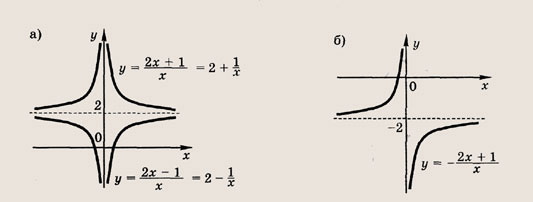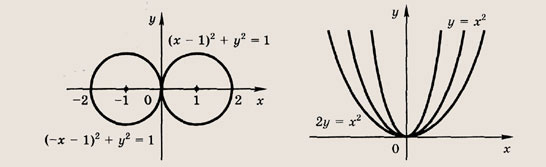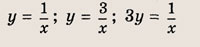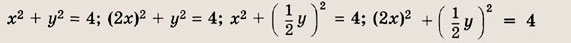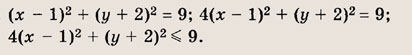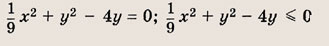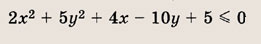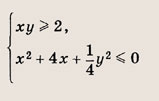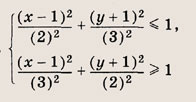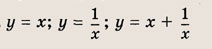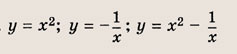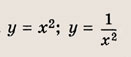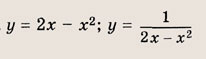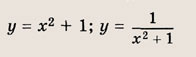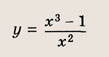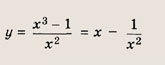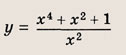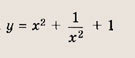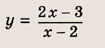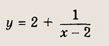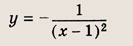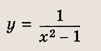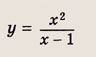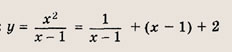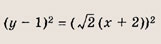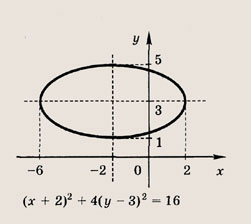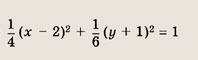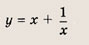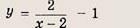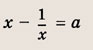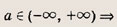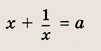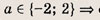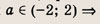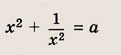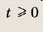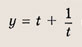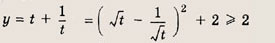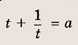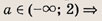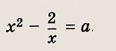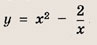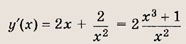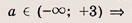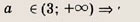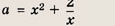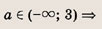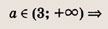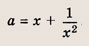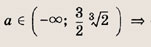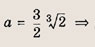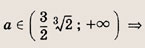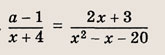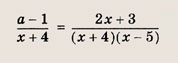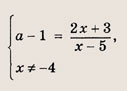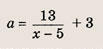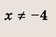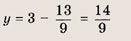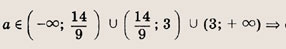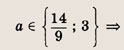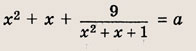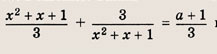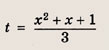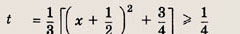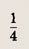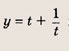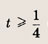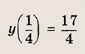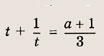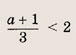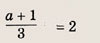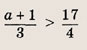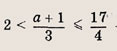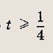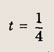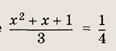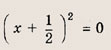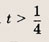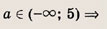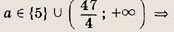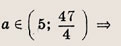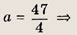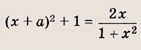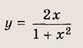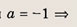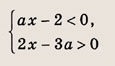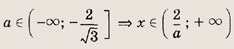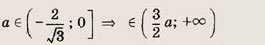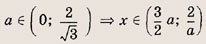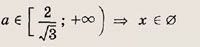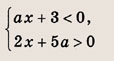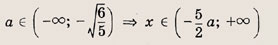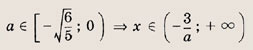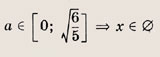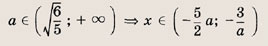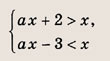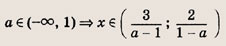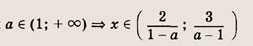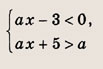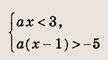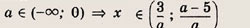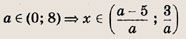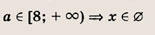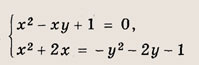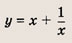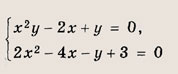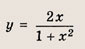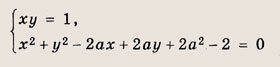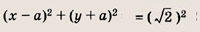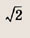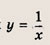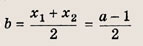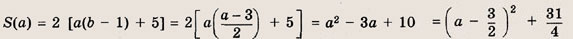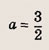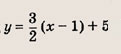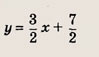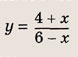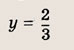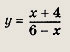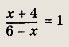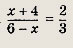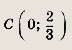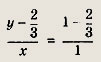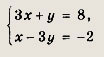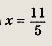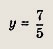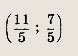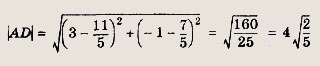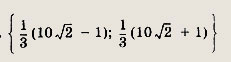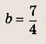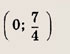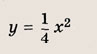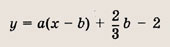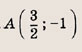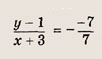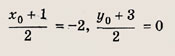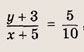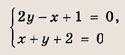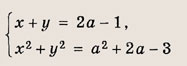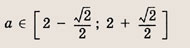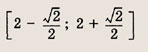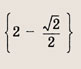Что такое гипербола парабола и прямая
Что такое гипербола парабола и прямая
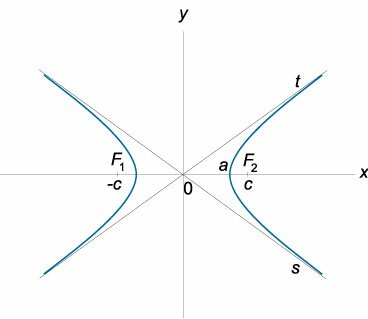
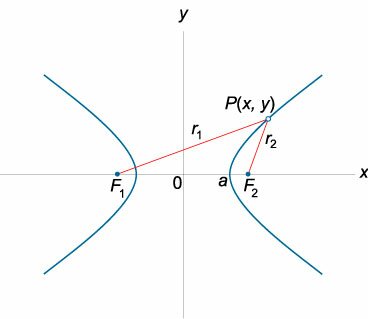
Модуль разности расстояний от любой точки гиперболы до ее фокусов является постоянной величиной:
\(\left| <
где \(
Уравнения асимптот гиперболы
\(y = \pm \large\frac\normalsize x\)
Соотношение между полуосями гиперболы и фокусным расстоянием
\(
где \(c\) − половина фокусного расстояния, \(a\) − действительная полуось гиперболы, \(b\) − мнимая полуось.
Уравнение правой ветви гиперболы в параметрической форме
\( \left\ < \begin
где \(a\), \(b\) − полуоси гиперболы, \(t\) − параметр.
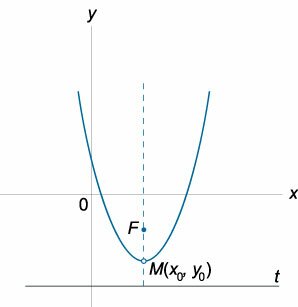
Координаты фокуса
\(F \left( <\large\frac
<2>\normalsize, 0> \right)\)
Координаты вершины
\(M \left( <0,0>\right)\)
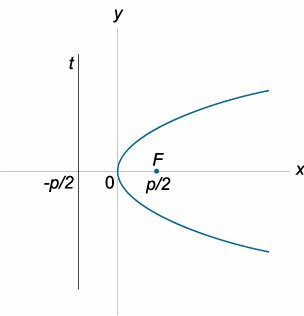
Уравнение параболы, ось симметрии которой параллельна оси \(Oy\)
\(A
или в эквивалентной форме
\(y = a
Уравнение директрисы
\(y =
<2>\normalsize\),
где \(p\) − параметр параболы.
Координаты фокуса
\(F\left( <
<2>\normalsize> \right)\)
Уравнение параболы с вершиной в начале координат и осью симметрии, параллельной оси \(Oy\)
\(y = a
Координаты вершины
\(M \left( <0,0>\right)\)
Графики прямой, параболы, гиперболы, с модулем
Пошаговое построение графиков.
«Навешивание» модулей на прямые, параболы, гиперболы.
Графики — самая наглядная тема по алгебре. Рисуя графики, можно творить, а если еще и сможешь задать уравнения своего творчества, то и учитель достойно это оценит.
Для понимания друг друга введу немного «обзываний» системы координат:
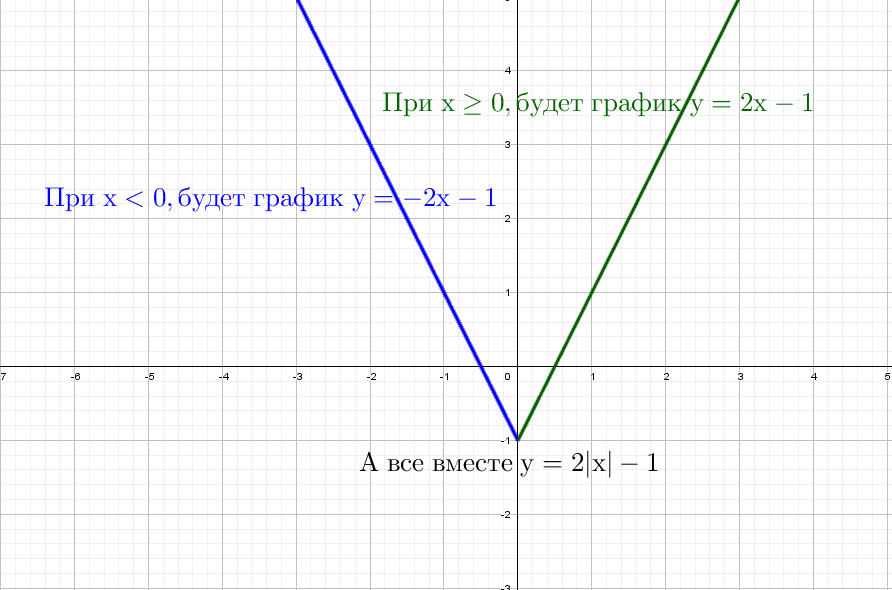
Для начала построим график прямой y = 2x − 1.
Не сомневаюсь, что ты помнишь. Я напомню себе, что через 2 точки можно провести одну прямую.
Возьмем значение X = 0 и Х = 1 и подставим в выражение y = 2x − 1, тогда соответственно Y = − 1 и Y = 1
Через данные две точки А = (0; −1) и B = (1; 1) проводим единственную прямую:
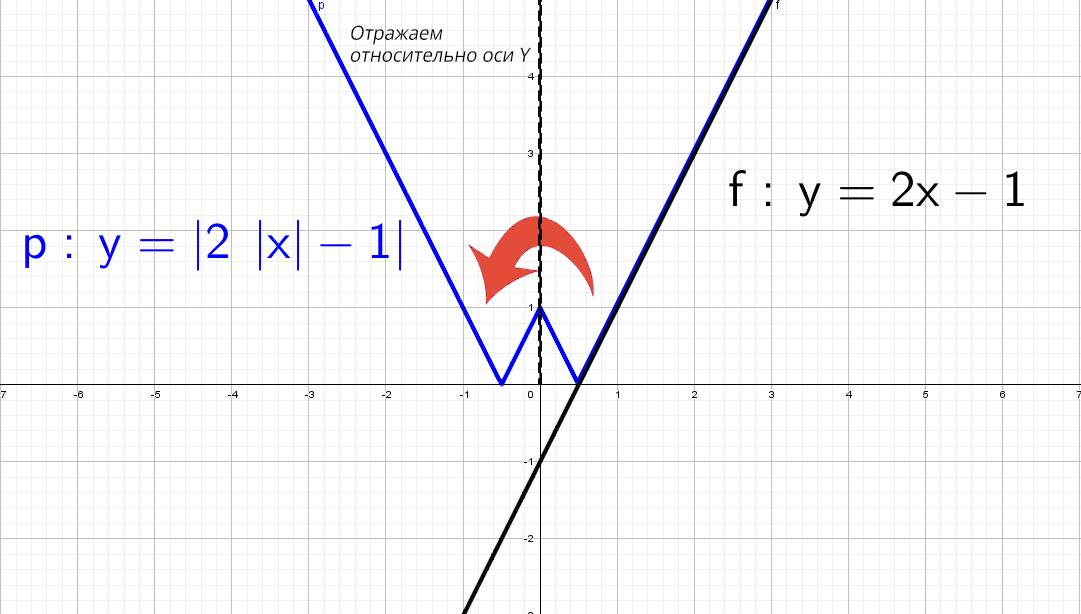
А если теперь добавить модуль y = |2x − 1|.
Значит, если модуль «надет» на весь график, то, что было в нижней части «−y», отразится в верхнюю (как будто сворачиваете лист по оси х и то, что было снизу, отпечатываете сверху).
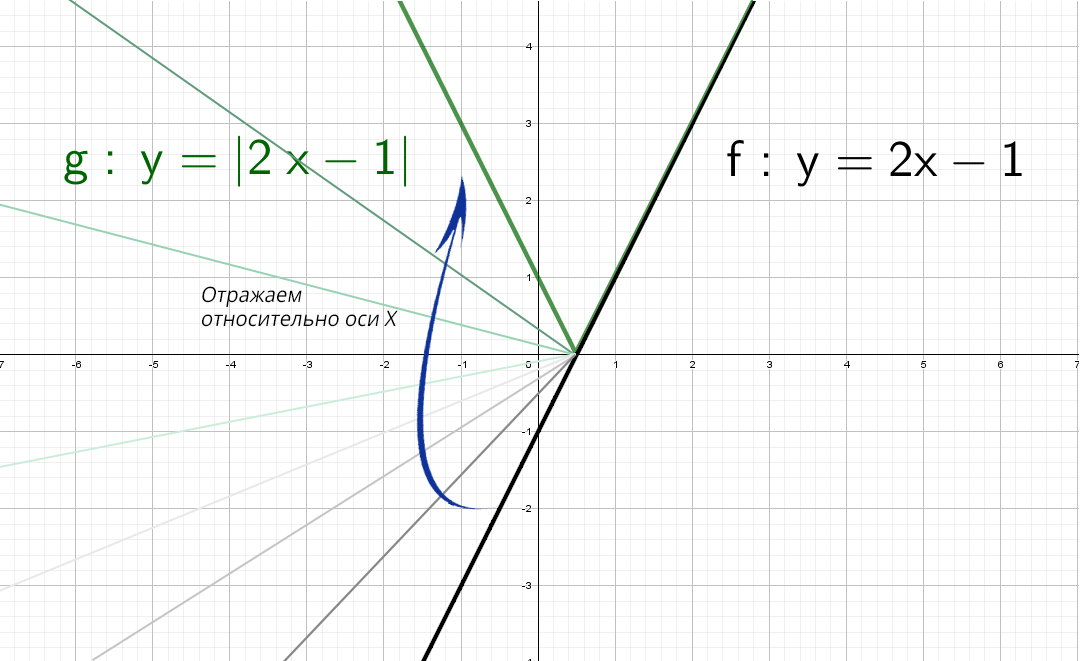
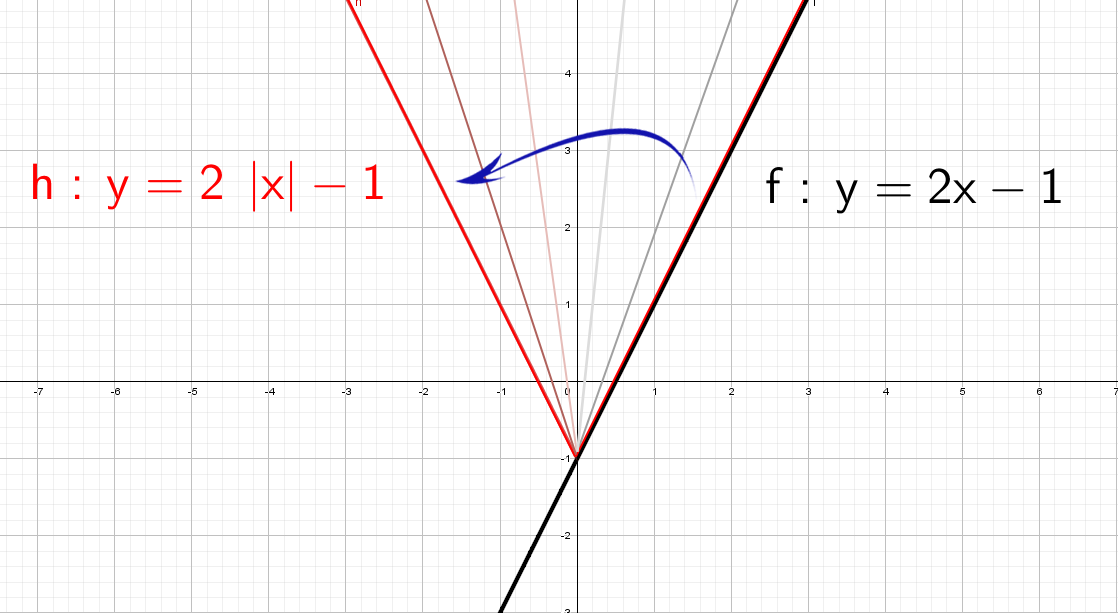
Красота! А как же будет выглядеть график, если надеть модуль только на «х»: y = 2|x| − 1?
Одна строчка рассуждений и рисуем:
Модуль на «x», тогда в этом случае x = −x, то есть все, что было в правой части, отражаем в левую. А то, что было в плоскости «−x», убираем.
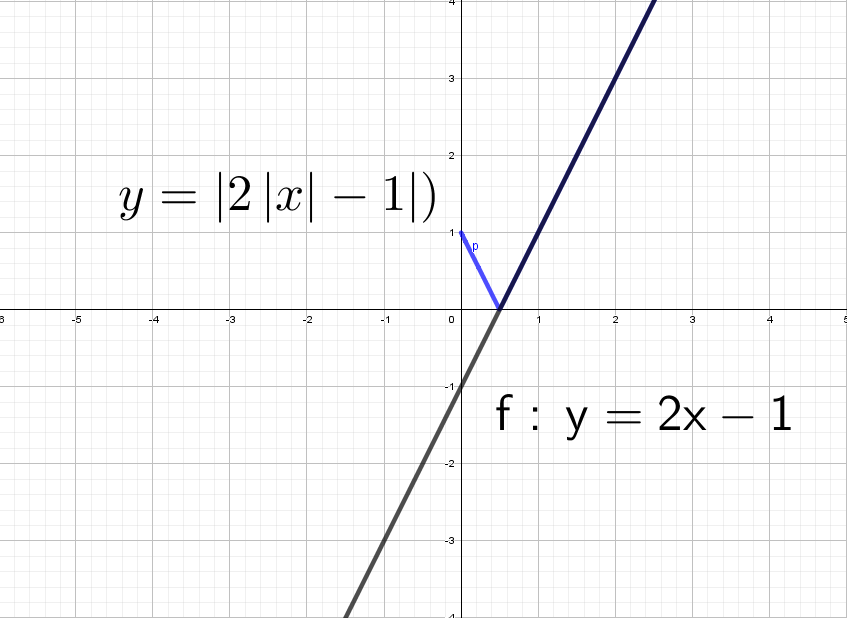
Смертельный номер: y = |2|x| − 1|.
Черную прямую y = 2x − 1 отражаем относительно оси Х, получим y = |2x − 1|. Но мы выяснили, что модуль на х влияет только на левую часть.
В правой части: y = |2x − 1| и y = |2|x| − 1| идентичны!
А после этого отражаем относительно оси «y» то, что мы получили справа налево:
Если ты человек амбициозный, то прямых тебе будет мало! Но то, что описано выше, работает на всех остальных графиках, значит делаем по аналогии.
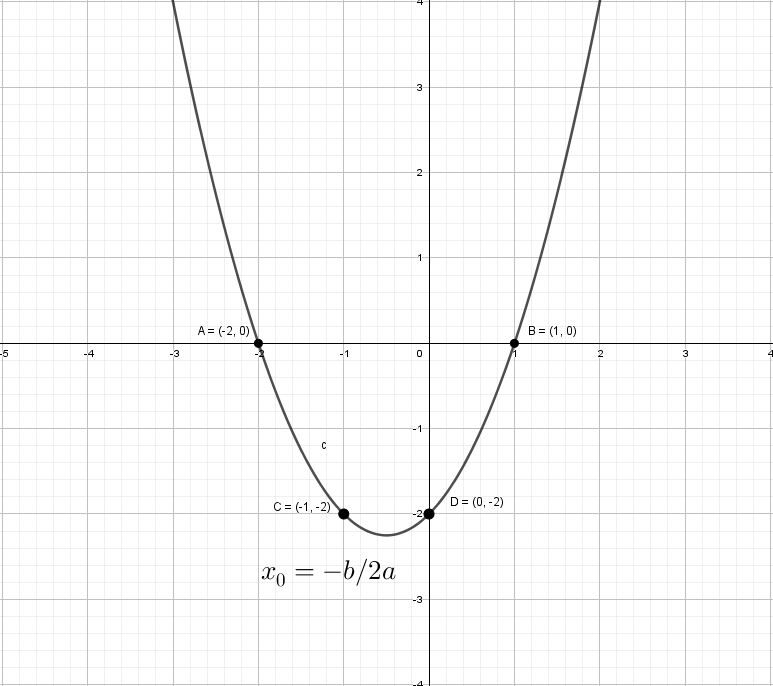
Можно найти вершину у параболы и взять пару точек для точного построения.
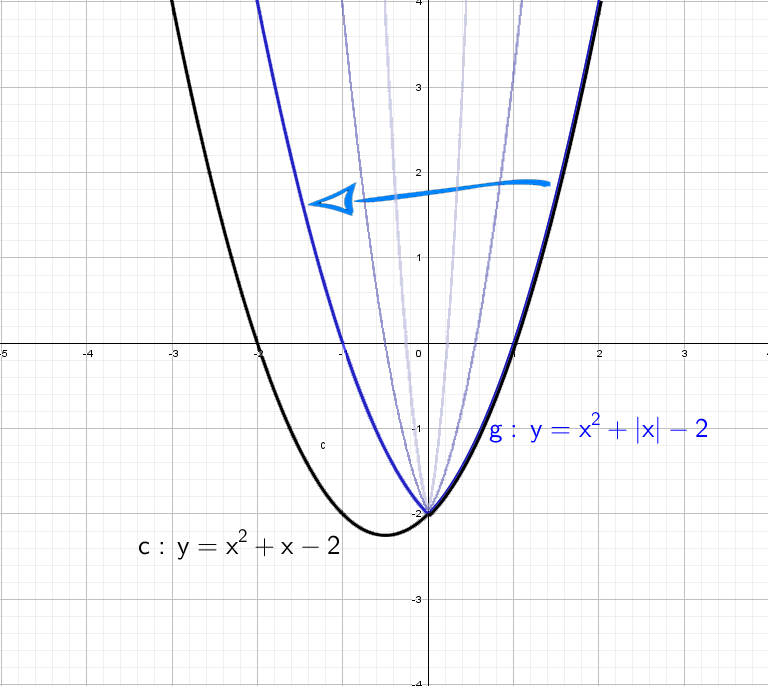
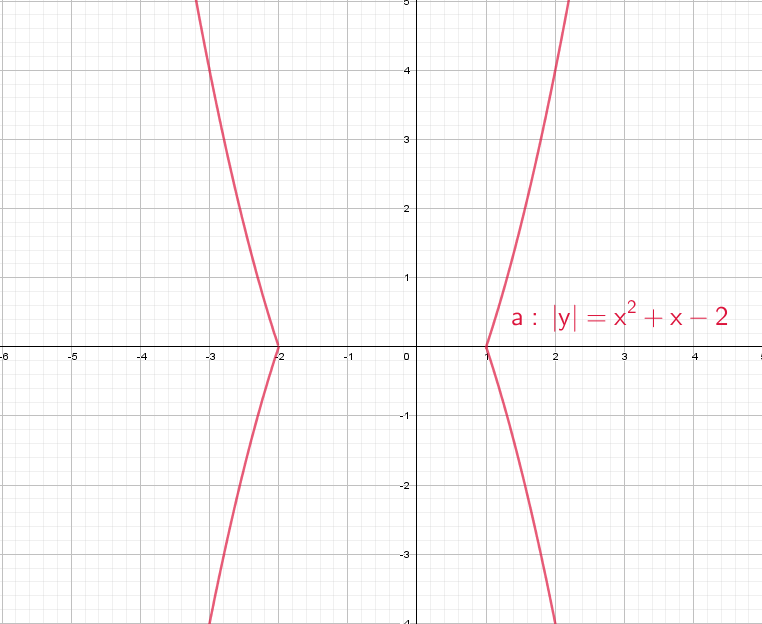
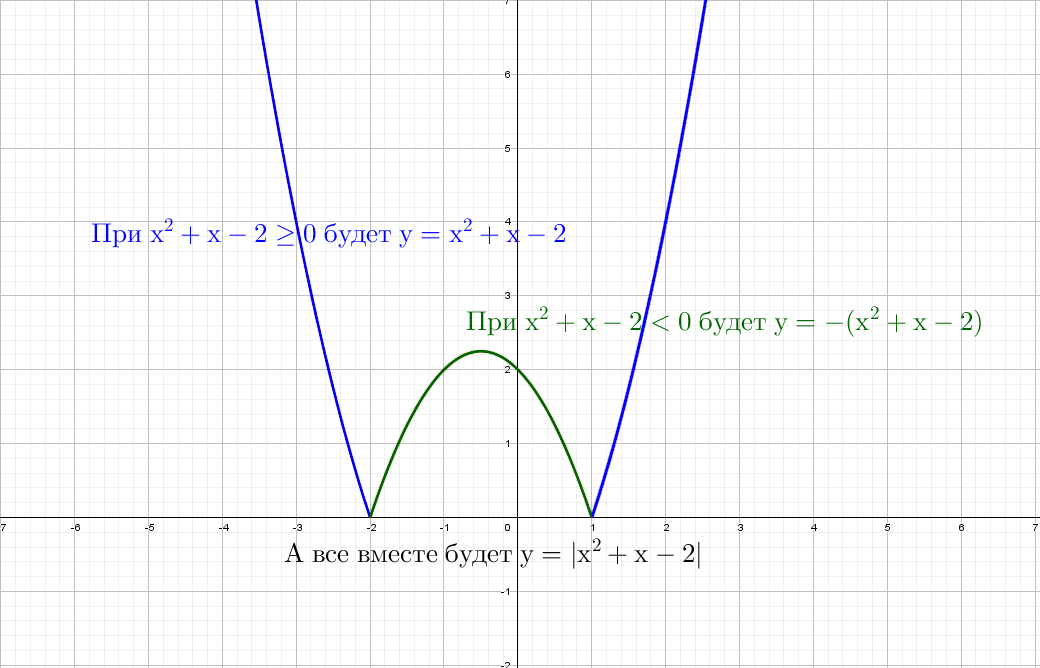
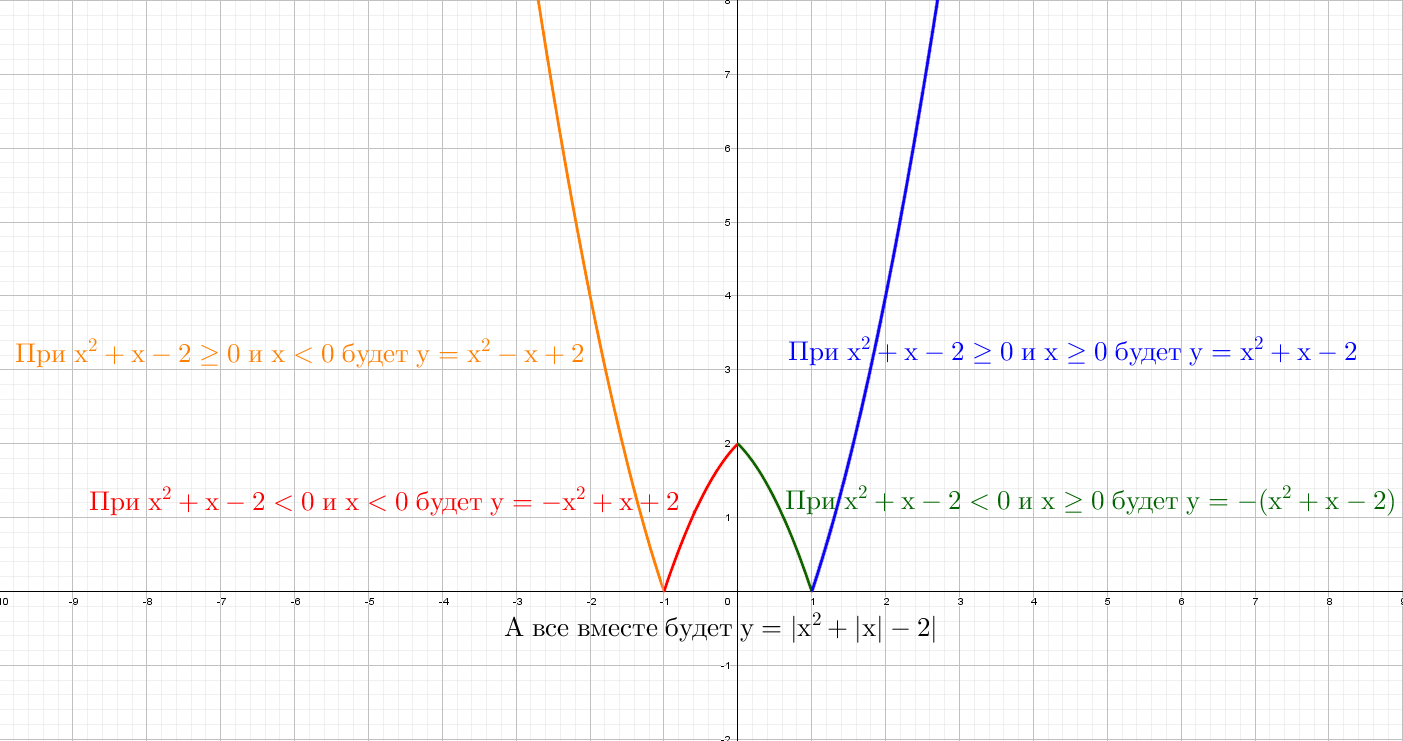
А как будет выглядеть график: y = |x²| + x − 2? Слышу: «Такого мы еще не проходили», а если подумаем? Модуль на x², он же и так всегда положителен, от модуля тут толку, как от стоп-сигнала зайцу − никакого.
При y = x² + |x| − 2 все так же стираем всю левую часть, и отражаем справа налево:
А дальше что мелочиться: рассмотри сразу остальные графики с модулем!
При положительных значениях «y» от модуля нет смысла − уравнения y = x² + x − 2, а при «−y» ничего не меняется, будет так же y = x² + x − 2!
Рисуем параболу в верхней части системы координат (где у > 0), а затем отражаем вниз.
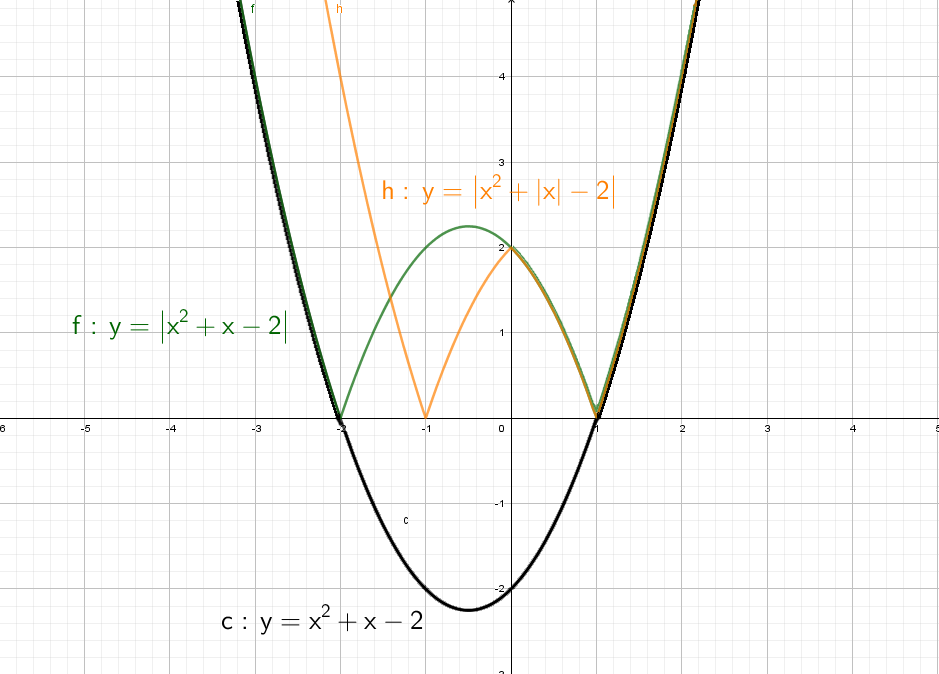
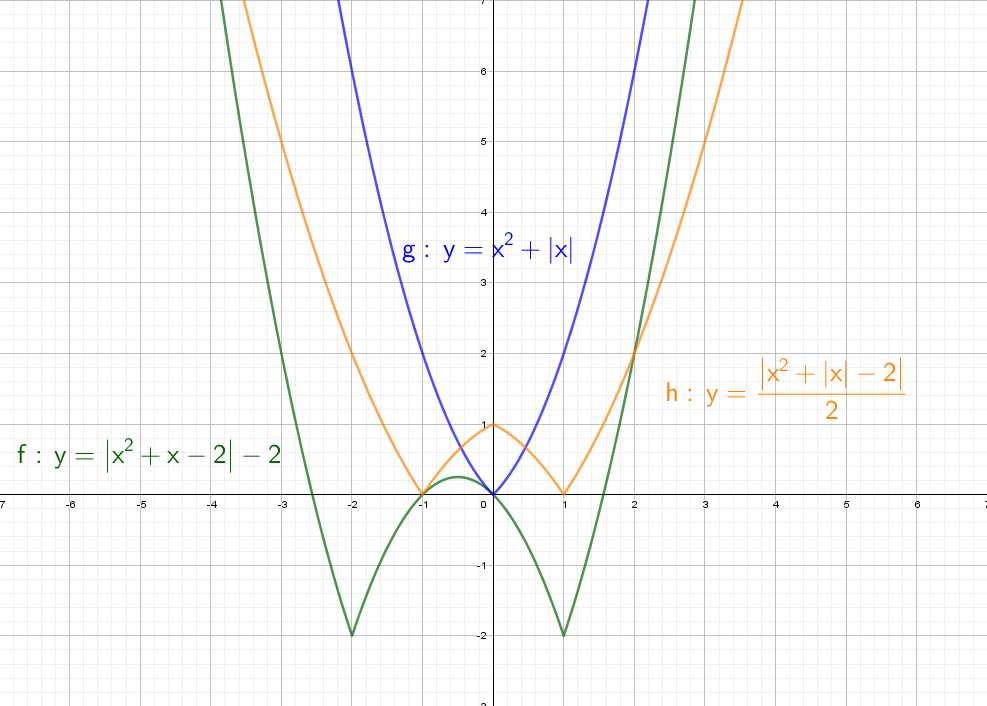
А теперь сразу комбо:
Cиний: похож на y = x² + |x| − 2, только поднят вверх. Строим график в правой части, а затем отражаем через ось Y влево.
Оранжевый: строим в правой части и отражаем относительно оси Х. Доходим до оси Y и отражаем все что было справа налево. Двойка в знаменателе показывает, что график будет «шире», расходится в бока он быстрее остальных.
Зеленый: Так же начинаем с правой части и отражаем относительно оси оси Y. Получается график y = |x² + x − 2|, но еще есть −2, поэтому опустим график на 2 вниз. Теперь параболы как бы отражается относительно Y = − 2.
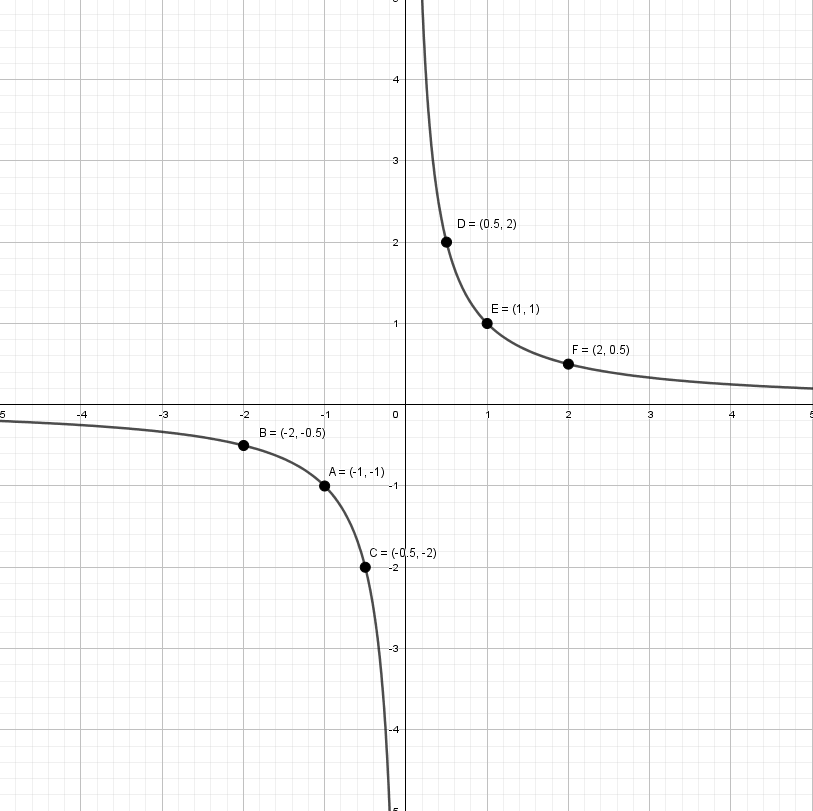
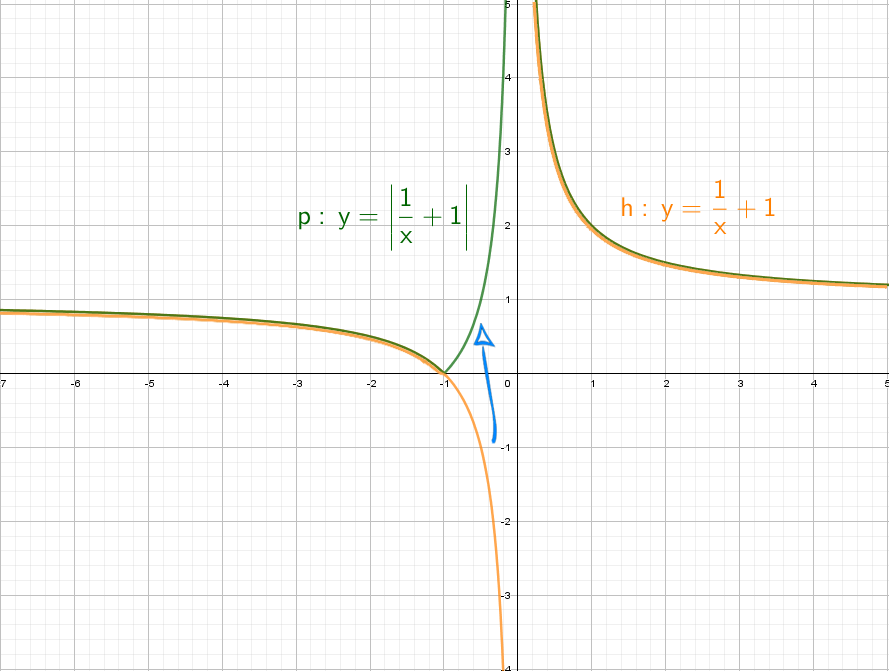
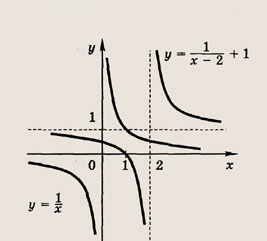
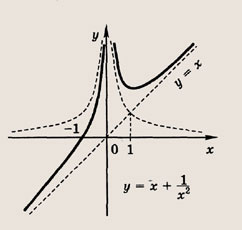
y = 1/x — простая гипербола, которую проще всего построить по точкам, 6-8 точек должно быть достаточно:
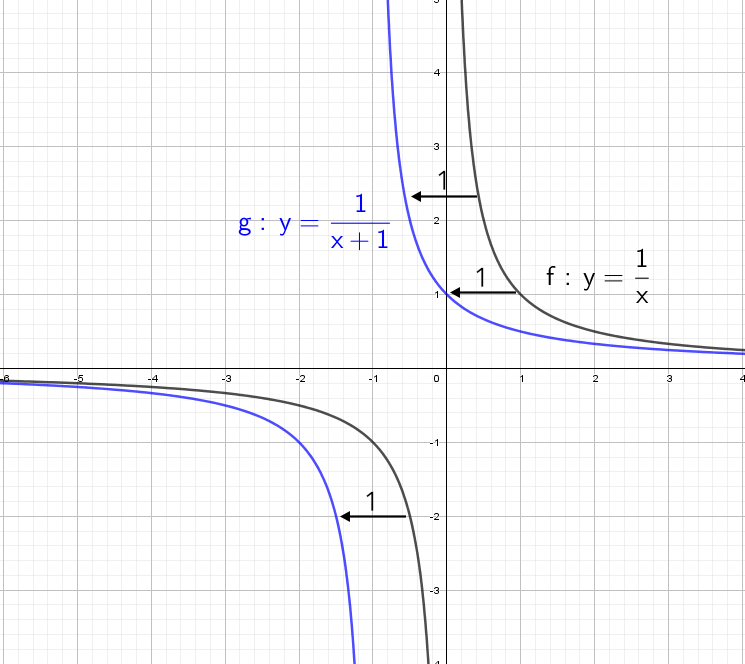
А что будет, если мы добавим в знаменателе «+1»? График сдвинется влево на единицу:
А что будет, если мы добавим в знаменателе « − 1»? График сдвинется вправо на единицу.
А если добавить отдельно «+1» y = (1/x) + 1? Конечно, график поднимется вверх на единицу!
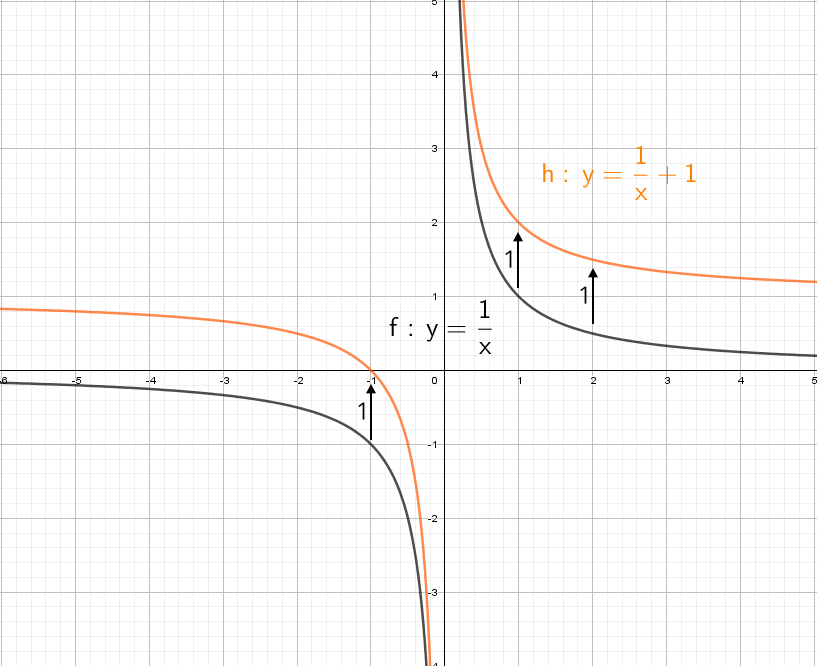
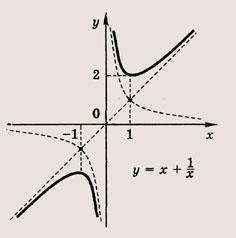
Теперь начнем «накручивать» модули: y = |1/x + 1| — отражаем все из нижней части в верхнюю.
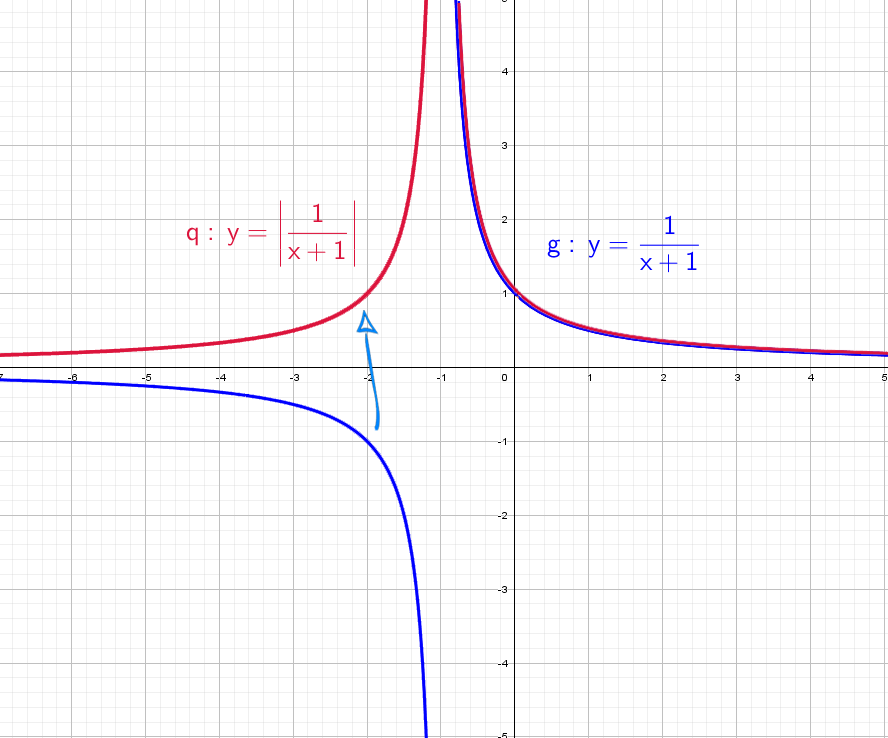
Возьмем другой модуль, мой амбициозный друг, раз ты дошел до этогог места: y = |1/(x + 1)|. Как и выше, когда модуль надет на всю функцию, мы отражаем снизу вверх.
Можно придумывать массу вариантов, но общий принцип остается для любого графика. Принципы повторим в выводах в конце статьи.
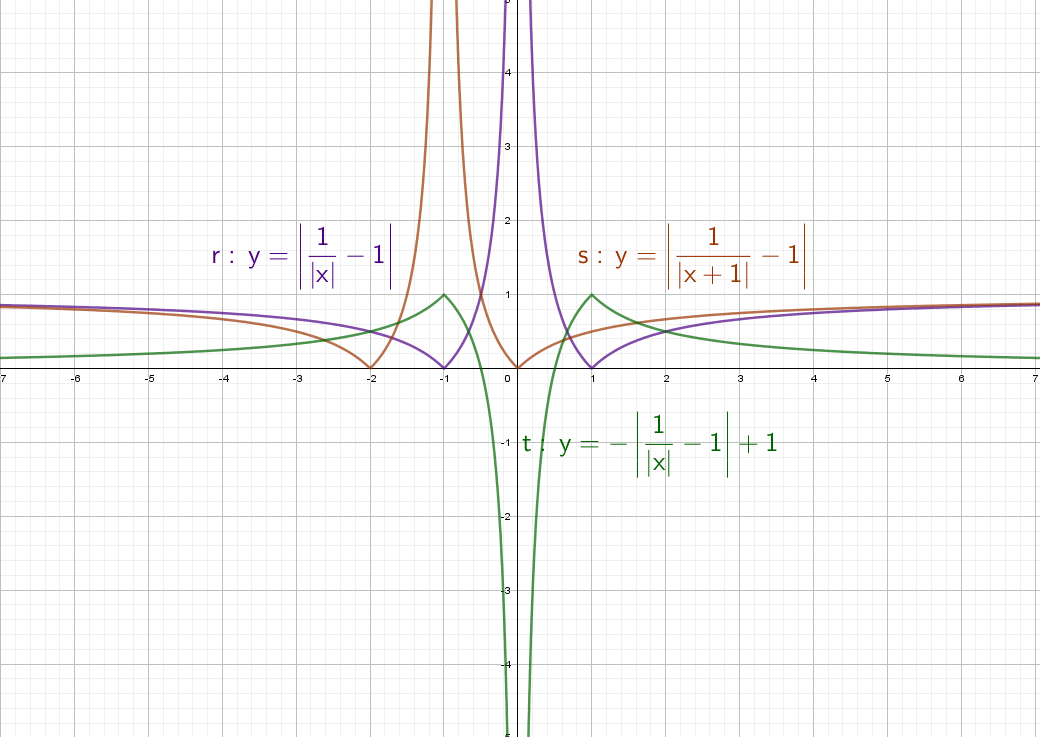
Фиолетовый: Вычитаем из дроби −1 и сдвигаем график вниз на единицу. Ставим модуль − отражаем все, что снизу вверх.
Оранжевый: Ставим +1 в знаменателе и график смещается влево на единицу. Вычитаем из дроби −1 и сдвигаем график вниз на единицу. А после этого ставим модуль − отражаем все, что снизу вверх.
Зеленый: Сначала получим фиолетовый график. После этого ставим «−» и отражаем график по горизонтали. Сгибаем лист по оси Х и переводим его вниз. Остается добавить +1, это значит, что его нужно поднять вверх на единицу.
Модули не так уж страшны, если еще вспомнить, что их можно раскрыть по определению:
И построить график, разбив его на кусочно-заданные функции.
Например для прямой:
Для параболы с одним модулем будет два кусочно-заданных графика:
C двумя модулями кусочно-заданных графиков будет четыре:
Построение графиков функций
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие функции
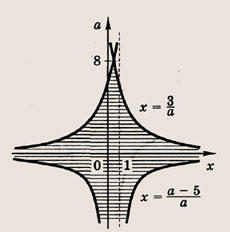
Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида 
Область значений — множество у, то есть это значения, которые может принимать функция.
Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
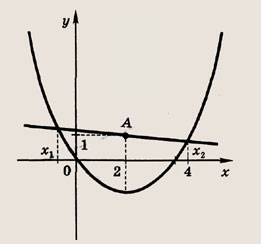
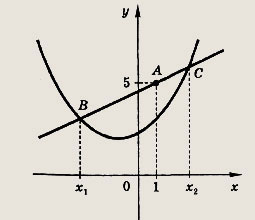
Понятие графика функции
Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.
График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.
Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.
Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.
В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.
Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:
Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.
Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.
Исследование функции
Важные точки графика функции y = f(x):
Стационарные точки — точки, в которых производная функции f(x) равна нулю.
Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.
Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.
Нули функции — это значения аргумента, при которых функция равна нулю.
Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.
Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:
Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.
Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.
Схема построения графика функции:
У нас есть отличные курсы по математике для учеников с 1 по 11 классы!
Построение графика функции
Чтобы понять, как строить графики функций, потренируемся на примерах.
Задача 1. Построим график функции
Упростим формулу функции:
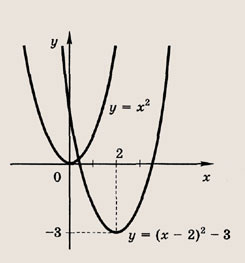
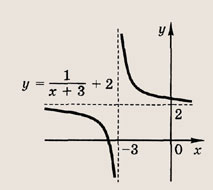
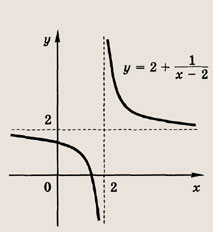
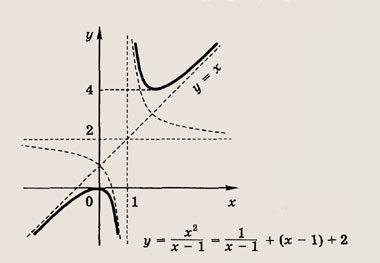
Задача 2. Построим график функции
Выделим в формуле функции целую часть:
График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции
Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.
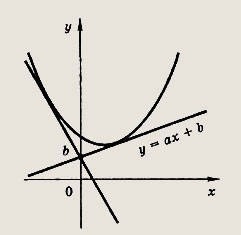
Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.
Вспомним, как параметры a, b и c определяют положение параболы.
Ветви вниз, следовательно, a 0.
Точка пересечения с осью Oy — c = 0.
Координата вершины 
Ветви вниз, следовательно, a 0.
Координата вершины 
| x | y |
| 0 | -1 |
| 1 | 2 |
| x | y |
| 0 | 2 |
| 1 | 1 |
| x | y |
| 0 | 0 |
| 1 | 2 |
k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.
Задача 5. Построить график функции
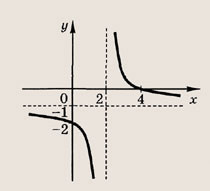
Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.
Нули функции: 3, 2, 6.
Промежутки знакопостоянства функции определим с помощью метода интервалов.
Вертикальные асимптоты: x = 0, x = 4.
Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.
Вот так выглядит график:
Задача 6. Построить графики функций:
б)
г)
д)
Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.
а)
Преобразование в одно действие типа f(x) + a.
Сдвигаем график вверх на 1:
б)
Сдвигаем график вправо на 1:
Сдвигаем график вправо на 1:
Сдвигаем график вверх на 2:
г)
Преобразование в одно действие типа
Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:
д)
Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.


Сжимаем график в два раза вдоль оси абсцисс:

Сдвигаем график влево на 1/2 вдоль оси абсцисс:

Отражаем график симметрично относительно оси абсцисс:
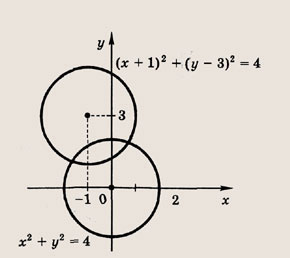
Что такое гипербола парабола и прямая
Прямая, окружность, парабола и гипербола.
Некоторые приемы построения графиков функций
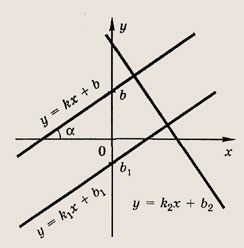
называется общим уравнением прямой. Мы уже знаем, что каждая прямая записывается таким уравнением и, обратно, каждое такое уравнение определяет прямую. Если уравнение прямой записано в виде у = kx + b, то число k называется ее угловым коэффициентом. При этом
т.е. совпадает с тангенсом угла наклона прямой L к оси Ох
Признаком параллельности двух прямых L и L1 является равенство их угловых коэффициентов: k = k1.
— уравнением прямой, проходящей через две данные точки А(х0; у0) и В(х1; y1).
Задание 1.
Ответ:
Задание 2.
Запишите уравнение прямой, проходящей через данную точку А(х0; у0) и образующей с осью Ох угол
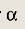
если:
а) 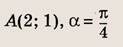
б)
Ответ:
в)
Задание 3.
Запишите уравнение прямой, параллельной прямой у = 2х + 3 и проходящей через точку А(-3; 2).
Ответ:
Задание 4.
Ответ:
Задание 5.
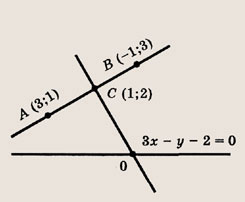
Используя общее уравнение прямой, проходящей через две заданные точки, для прямой (АВ) имеем
Задание 6.
• Пусть А(х0; у0), B(х1у1) — две данные точки; тогда точка С
лежит на прямой, проходящей через точки А и В, и делит отрезок АВ пополам. Используйте этот факт при решении задний 7, 8.
Решение:
Поэтому уравнения прямых, перпендикулярных данной прямой, имеют вид
Подставляя в это равенство координаты точки М1 (2; 1), находим
Отсюда следует нужное нам уравнение.
Ответ:
Задание 7.
Решение:
Найдем координаты точки пересечения этих прямых, для чего решим систему уравнений
откуда х = 3, у = 1. Точка С(3; 1) является серединой отрезка PQ, где Р (-5; 13), a Q(x0; у0) — искомая точка. Поэтому
Ответ:
Задание 8.
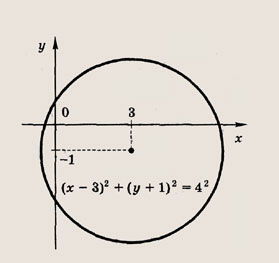
определяет окружность радиуса R с центром в точке С(х0; у0).
Решение:
Следовательно, прямая, параллельная данным и проходящая посередине между ними, имеет уравнение 2х + Зу + 6 = 0 и проходит через точку C
где С — середина отрезка АВ. Отсюда находим
а тогда уравнение искомой прямой можно записать в виде:
Ответ:
Задание 9.
Запишите уравнение окружности, если:
б) окружность проходит через точку А(2; 6), а ее центр совпадает с точкой С(-1; 2);
в) точки А(3; 2) и В(-1; 6) являются концами одного из диаметров этой окружности.
Ответ:
Задание 10.
Решение:
— радиус искомой окружности.
Ответ:
Задание 11.
Решение:
откуда О (2; 4). Радиус искомой окружности равен длине отрезка ОВ, т. е.
Ответ:
Задание 12.
Запишите уравнение прямой, проходящей через центры двух данных окружностей:
Ответ:
Задание 13.
Указание:
Ответ:
Задание 14.
Установите, что каждое из следующих уравнений определяет параболу, найдите координаты ее вершины А и координаты точек пересечения с осями координат:
Ответ:
а) А(1; 3); с осью Ох не пересекается; С (0; 7);
Задание 15.
Найдите квадратный трехчлен, наибольшее значение которого, равное 3, достигается при х = 2, если известно, что его график проходит через точку О(0; 0).
Решение:
Ответ:
Задание 16.
График квадратного трехчлена, свободный член которого равен 1, симметричен относительно прямой х + 2 = 0 и проходит через точку А(2; 7). Запишите этот квадратный трехчлен.
Ответ:
Задание 17.
Решение:
Из условия следует, что квадратный трехчлен имеет вид у = а(х + 1) 2 + b. Подставляя в это равенство координаты точек М1(-2; 2) и М2(2; 26), получаем систему
Ответ:
Задание 18.
Ответ:
Задание 19.
Находим координаты точек А и В. Решаем уравнение
Уравнение искомой параболы имеет вид у = ах 2 + bх. Подставляя в это равенство координаты точек А и В, приходим к системе:
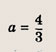
Ответ:
Задание 20.
Решение:
Ответ:
Задание 21.
Запишите уравнение параболы, проходящей через данные точки А, В и С, если:
a, b, d — действительные числа и
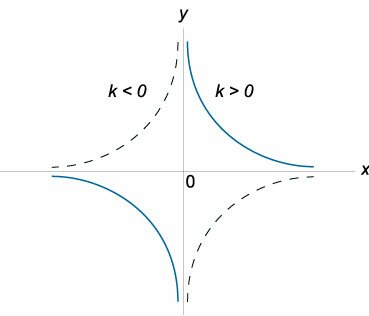
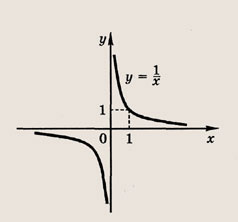
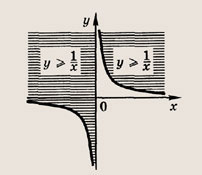
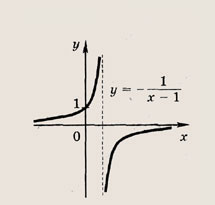
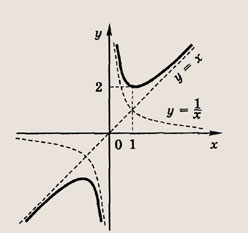
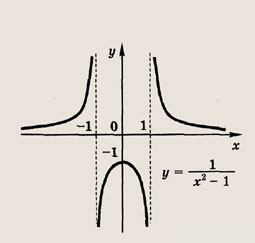
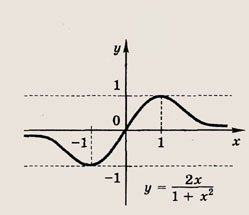
называется дробно-линейной функцией. Кривая, которая служит графиком этой функции, называется гиперболой. Ниже мы установим, что график дробно-линейной функции можно получить из графика простейшей дробно-линейной функции
(графика обратной пропорциональной зависимости) с помощью параллельного переноса,
отражения и растяжения (сжатия) вдоль координатных осей. График функции
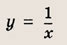
изображен на рис.
Отметим, что прямые у =0 и х=0 (координатные оси) являются асимптотами гиперболы
а точка О(0; 0) — ее центром симметрии.
Указание:
Запишите уравнение искомой параболы в виде у = ах 2 + bх + с и подставьте в это равенство координаты данных в условии точек.
Ответ:
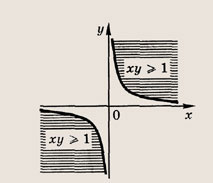
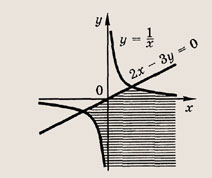
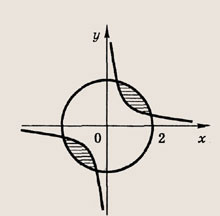
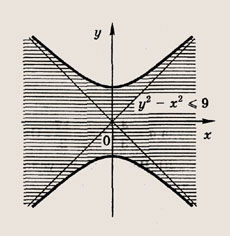
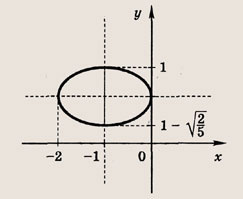
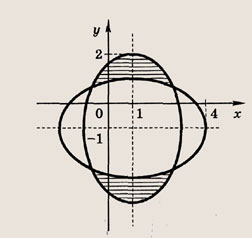
Постройте графики следующих функций и уравнений. Штриховкой укажите области, координаты точек которых удовлетворяют указанным неравенствам (22—26):
Задание 22.
Ответ:
Задание 23.
Почему в заданиях 22 и 23 получаются различные заштрихованные области?
Ответ:
Задание 24.
Ответ:
Задание 25.
Ответ:
Задание 26.
(эта кривая также является гиперболой).
Ответ:
Задание 27.
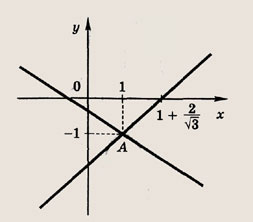
Составьте уравнения касательных к гиперболе
Напомним некоторые приемы, которые часто используются при построении графиков функций. При этом предполагается, что график функции у = f(x) (или уравнения f(x, у) = 0) известен.
• Сдвиги (параллельные переносы) вдоль координатных осей.
Пусть построен график функции у = f(x). Тогда:
Решение:
Приравнивая нулю дискриминант квадратного уравнения
Ответ:
Постройте графики следующих функций и уравнений (28—34):
Задание 28.
Ответ:
Задание 29.
Ответ:
Задание 30..
Ответ:
Задание 31.
Ответ:
Задание 32.
Ответ:
Задание 33.
Указание:
Преобразуйте уравнение к виду
Ответ:
Задание 34.
Указание:
Преобразуйте уравнение к виду
Ответ:
Задание 35.
Запишите уравнение образа каждой из них при параллельном переносе, если ее центр смещается в точку С(-1; 2).
Решение б):
Ответ:
Задание 36.
Запишите уравнение образа параболы у = х 2 + + 2х + 2 при параллельном переносе, если ее вершина смещается в точку A(x0; у0), где
Решение б).
Парабола у = х 2 + 2х + 2 = (х + 1) 2 + 1 получается из параболы у = х 2 переносом вершины в точку А (-1; 1). Если вершина этой параболы при параллельном переносе сместится в точку А (-3; 4), то ее уравнение примет вид у = (х + З) 2 + 4.
Ответ:
Задание 37.
Запишите уравнение образа гиперболы
при параллельном переносе, если ее центр симметрии смещается вточку А(-3; 1).
• Зеркальное отражение относительно координатных осей.
Пусть задан график функции у = f(x) (или уравнения f(x, у) = 0). Тогда:
1) графики функций у = f(x) и у = f(-x) (уравнений f(x, у) = 0 и f(-x, у) = 0) симметричны относительно оси Оу,
Постройте графики следующих функций и уравнений (38—42).
Ответ:
Задание 38.
Ответ:
Задание 39.
Ответ:
Задание 40.
Ответ:
Задание 41.
Ответ:
Задание 42.
• Растяжение (сжатие) графика вдоль координатных осей.
Пусть задан график функции у = f(x) и число k > 0. Тогда:
1) график функции у = f(kx) получается из графика функции у = f(x) сжатием вдоль оси Ох в k раз, если
2) график функции у = kf(x) получается из графика функции у = f(x) растяжением вдоль оси Оу в k раз, если
Отметим также, что графики уравнений f(kx, у) = 0, f(x, ky) = 0 получаются из графика уравнения f(x, у) = 0 сжатием вдоль соответствующей координатной оси в k раз, если k > 1 (при k
Постройте графики следующих функций и уравнений (43—50). Отметьте штриховкой области, координаты точек которых удовлетворяют указанным неравенствам.
Ответ:
Задание 43.
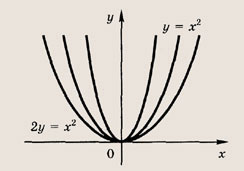
у = х 2 ; у = (2х) 2 ; 2у = х 2
Ответ:
Задание 44.
Ответ:
Задание 45.
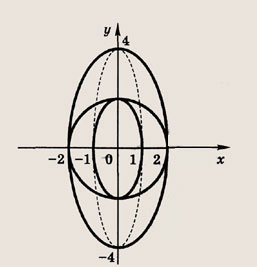
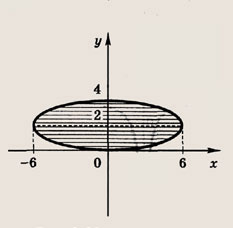
(кривая, которая получается при сжатии окружности вдоль координатных осей, называется эллипсом).
Ответ:
Задание 46.
Ответ:
Задание 47.
Ответ:
Задание 48.
Ответ:
Задание 49.
Ответ:
Задание 50.
• При построении эскизов графиков элементарных функций часто используются и такие приемы, как сложение (вычитание) и деление (умножение) графиков.
Постройте графики следующих функций (51—57):
Ответ:
Задание 51.
Ответ:
Задание 52.
Ответ:
Задание 53.
Ответ:
Задание 54.
Ответ:
Задание 55.
Ответ:
Задание 56.
Указание:
Ответ:
Задание 57.
Указание:
Ответ:
Используя различные приемы, постройте графики следующих функций и уравнений (58—71):
Задание 58.
Ответ:
Задание 59.
Указание:
Ответ:
Задание 60.
Указание:
Ответ:
Задание 61.
Ответ:
Задание 62.
Ответ:
Задание 63.
Ответ:
Задание 64.
Указание:
Ответ:
Задание 65.
Указание:
Ответ:
Задание 66.
Указание:
Ответ:
Задание 67.
Указание:
Ответ:
Задание 68.
Ответ:
Задание 69.
Указание:
Ответ:
Задание 70.
Указание:
Ответ:
Задание 71.
Указание:
Ответ:
Найдите число различных решений уравнений в зависимости от а (72—80):
Задание 72.
Ответ:
Задание 73.
Ответ:
Задание 74.
Решение:
Положим х 2 = t. Тогда
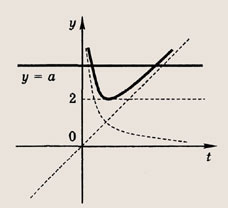
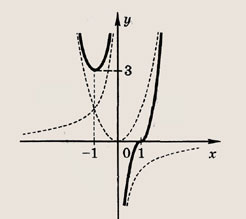
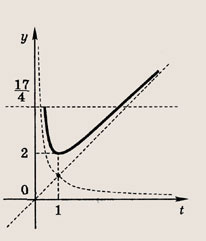
Построим при t > 0 график функции
при t > 0, причем наименьшее значение у = 2 достигается при t = 1, то получаем: при
а уравнение
не имеет положительных решений, при а = 2 => одно решение; а > 2 => два решения. Теперь находим число решений исходного уравнения.
Ответ:
нет решений, при а = 2 => два решения; при
Задание 75.
Решение:
Построим график функции
Поэтому получаем следующий ответ.
Ответ:
одно решение; при а = 3 => два решения; при
Задание 76.
Указание:
Запишите уравнение в виде
Далее см. решение задачи 75.
Ответ:
одно решение; при а = 3 => два решения; при
Задание 77.
Запишите уравнение в виде
Ответ:
Задание 78.
Решение:
Запишем уравнение в виде
График этой функции — гипербола, принимающая все значения, кроме у = 3, по одному разу. Поскольку
нужно также исключить значение
Ответ:
Задание 79.
Решение:
Запишем уравнение в виде
Сначала найдем число решений уравнения
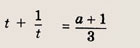
не меньших
Построим график функции
а наименьшее значение y(t) равно 2. Поэтому уравнение
не имеет решении, при
— имеет одно решение, а при
— два решения, удовлетворяющих условию
Отдельно рассмотрим случай
имеет одно решение (мы находим число различных решений). При всех остальных
уравнение х 2 + х + 1 = 3t будет иметь два различных решения. Теперь легко записываем ответ.
Ответ:
четыре решения; при
Задание 80.
(х 2 + 1)(х 2 + 2ах + а 2 + 1) = 2х
Указание:
Запищите уравнение в виде
и постройте графики функций
Ответ:
одно решение х = 1, при других а решений нет.
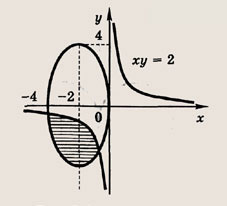
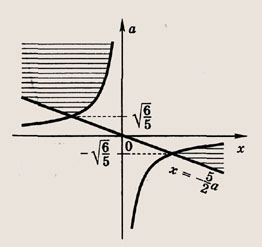
Решите системы неравенств и уравнений (81—87):
Задание 81.
Ответ:
Задание 82.
Решение:
На координатной плоскости (х, а) штриховкой отметим точки, координаты которых удовлетворяют нашей системе неравенств
Ответ:
Задание 83.
Ответ:
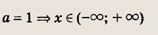
при
Задание 84.
Решение:
Перепишем неравенства в виде
и штриховкой на координатной плоскости (х; а) отметим точки, координаты которых удовлетворяют этой системе неравенств
Записываем решение данной системы.
Ответ:
Задание 85.
Указание:
и (х + 1) 2 + (у + 1) 2 =1
Ответ:
Задание 86.
Указание:
Постройте графики функций
Ответ:
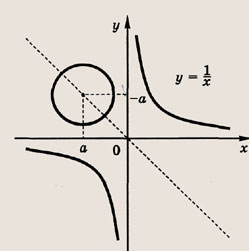
Задание 87.
Решение:
Запишем второе уравнение в виде
Это окружность радиуса
Пересечение с гиперболой
Ответ:
при других а решений нет.
Задание 88.
Решение:
имеют абсциссы x1и х2, являющиеся корнями квадратного уравнения
Ответ:
Задание 89.
Прямая проходит через точку А(1; 5) и пересекает параболу у = х 2 + х+1 в точках, сумма ординат которых наименьшая. Запишите уравнение этой прямой.
Решение:
имеют абсциссы x1 и х2, являющиеся корнями квадратного уравнения
а сумма ординат точек пересечения равна
Следовательно, сумма ординат наименьшая при
Искомое уравнение имеет вид
Ответ:
Задание 90.
Ответ:
Задание 91.
и проходящую через точки этой линии с ординатами у = 1 и
Решение:
Находим точки В и С пересечения прямой с кривой
откуда х= 1, т.е. В (1; 1);
Записываем уравнение прямой, проходящей через точки В и С:
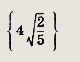
Вычисляем расстояние между точками А(3;-1) и D
Ответ:
Задание 92.
Найдите длину перпендикуляра, опущенного из точки А(5; 0) на касательную к параболе у = х 2 + 3, проведенную из точки В(0; 1).
Ответ:
Задание 93.
На оси ординат найдите точку, через которую проходят две взаимно перпендикулярные касательные к графику функции
Решение:
Уравнение касательной имеет вид у = ах + b
Приравнивая нулю дискриминант квадратного уравнения
Ответ:
Задание 94.
Указание:
Запишите уравнения касательных в виде
Далее см. решение задачи 93.
Ответ:
Задание 95.
Решение:
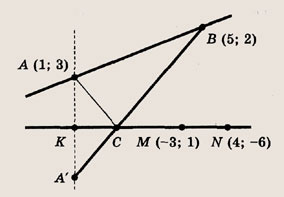
— это точка пересечения прямых (MN) и (А’В), где А’ — точка, симметричная A относительно прямой (MN) (см. задачу 7). Подумайте, почему это так? Теперь последовательно находим:
1) уравнение прямой (MN):
2) уравнение прямой (АА’):
3) координаты точки К, т. е. точки пересечения прямых (MN) и (АА):
4) координаты точки А (х0, у0); имеем
5) уравнение прямой (А’В):
6) координаты искомой точки С:
Ответ:
Задание 96.
Даны точка А(5; 7) и угол, уравнения сторон которого имеют вид у = 0 и у = х+5. Точки В и С лежат на разных сторонах угла. Найдите наименьшее значение периметра треугольника ABC.
Указание:
Наименьший периметр треугольника ABC равен длине отрезка PQ, где Р — точка, симметричная А относительно прямой у = 0, a Q — точка, симметричная А относительно прямой у = х + 5.
Ответ:
Задание 97.
Числа х, у и а удовлетворяют системе уравнений
При каком значении а произведение ху принимает наименьшее возможное значение?
Указание:
Сначала выясните, при каких а данная система имеет решение. Эти значения
Далее из системы выразите произведение ху через а и найдите минимум полученной функции на отрезке
Ответ