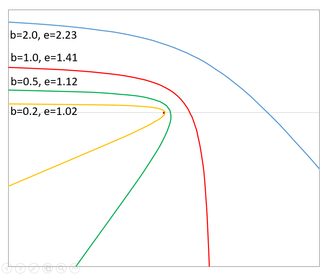
Что такое гиперболическая траектория
Гиперболическая траектория
В рамках стандартных предположений тело, движущееся вдоль такой траектории, сможет удалиться на бесконечность, сохранив ненулевую скорость относительно центрального тела. По аналогии с параболической траекторией все гиперболические траектории являются траекториями ухода. Орбитальная энергия в расчете на единицу массы является положительной величиной.
Пролёты мимо планет, используемые при гравитационном манёвре, могут быть представлены в сфере тяготения как гиперболические траектории.
Связанные понятия
Упоминания в литературе
Связанные понятия (продолжение)
В математике и физике барице́нтр, или геометри́ческий центр, двумерной области — это среднее арифметическое положений всех точек фигуры. Определение распространяется на любой объект в n-мерном пространстве — барицентр является средним положением всех точек фигуры по всем координатным направлениям. Неформально — это точка равновесия фигуры, вырезанной из картона в предположении, что картон имеет постоянную плотность и гравитационное поле постоянно по величине и направлению.
Межзвёздные объекты — это объекты или кометы, которые существуют в межзвёздном пространстве, не связанные силами тяготения с какой-либо звездой. Первым обнаруженным известным межзвёздным объектом является 1I/Оумуамуа. Межзвёздный объект может быть выявлен только если он проходит через нашу Солнечную систему вблизи от Солнца или если он отделился от облака Оорта и начал двигаться по сильно вытянутой гиперболической орбите, не связанной с гравитацией Солнца. Объекты со слабыми гиперболическими траекториями.
Земля-кроссеры — это околоземные астероиды, орбиты которых пересекают орбиту Земли. Перигелий орбиты у таких астероидов располагается внутри орбиты Земли, то есть он меньше афелия Земли (1,017 а. е.), но больше её перигелия (0,983 а. е.).
Ниже представлена совокупность списков примечательных астероидов Солнечной системы. В данной статье термин «астероид» обозначает малую планету до орибиты Юпитера, включая карликовую планету Цереру. Для получения полного списка малых планет смотрите список астероидов.
В астродинамика или же небесная механика, а гиперболическая траектория это траектория любого объекта вокруг центральный орган с более чем достаточной скоростью, чтобы избежать гравитационного воздействия центрального объекта. Название происходит от того, что согласно Ньютоновская теория такая орбита имеет форму гипербола. В более технических терминах это может быть выражено условием, что орбитальный эксцентриситет больше единицы.
Согласно упрощенным предположениям, тело, движущееся по этой траектории, будет двигаться к бесконечности, устанавливая конечную избыточную скорость относительно центрального тела. Аналогично параболические траектории, все гиперболические траектории также траектории ухода. В удельная энергия орбиты гиперболической траектории положительна.
Планетарные облеты, используемые для гравитационные рогатки, можно описать в пределах планеты сфера влияния с использованием гиперболических траекторий.
Содержание
Параметры, описывающие гиперболическую траекторию
Подобно эллиптической орбите, гиперболическая траектория для данной системы может быть определена (без учета ориентации) ее большой полуосью и эксцентриситетом. Однако для гиперболической орбиты другие параметры могут быть более полезными для понимания движения тела. В следующей таблице перечислены основные параметры, описывающие путь тела, следующего по гиперболической траектории вокруг другого при стандартных предположениях, и формулы, связывающие их.
Большая полуось, энергия и гиперболическая избыточная скорость
Обратите внимание, что полная энергия положительна в случае гиперболической траектории (тогда как она отрицательна для эллиптической орбиты).
Эксцентриситет и угол между заходом на посадку и вылетом
Параметр удара и дальность максимального сближения
В прицельный параметр это расстояние, на которое тело, если бы оно продолжало двигаться невозмущенным путем, могло бы пропустить центральное тело на своем ближайший подход. Для тел, испытывающих гравитационные силы и следующих по гиперболическим траекториям, он равен малой полуоси гиперболы.
В ситуации, когда космический корабль или комета приближается к планете, прицельный параметр и избыточная скорость будут известны точно. Если центральное тело известно, то теперь можно определить траекторию, включая то, насколько близко приближающееся тело будет в перицентре. Если он меньше радиуса планеты, следует ожидать удара. Расстояние наибольшего сближения или перицентрическое расстояние определяется как:
Итак, если приближается комета земной шар (эффективный радиус
6400 км) со скоростью 12,5 км / с (примерная минимальная скорость сближения тела, идущего с внешней стороны). Солнечная система), чтобы избежать столкновения с Землей, параметр удара должен быть не менее 8600 км, или на 34% больше радиуса Земли. Тело приближается Юпитер (радиус 70000 км) от внешней части Солнечной системы со скоростью 5,5 км / ч, во избежание столкновения потребуется, чтобы параметр удара был не менее 770 000 км или в 11 раз больше радиуса Юпитера.
Если масса центрального тела неизвестна, его стандартный гравитационный параметр и, следовательно, его масса могут быть определены путем отклонения меньшего тела вместе с параметром удара и скоростью приближения. Поскольку обычно все эти переменные могут быть определены точно, пролет космического корабля даст хорошую оценку массы тела.
Уравнения движения
Позиция
Связь между истинной аномалией θ и эксцентрическая аномалия E (в качестве альтернативы гиперболическая аномалия ЧАС) является: [2]
Средняя аномалия пропорциональна времени
Угол траектории полета
Скорость
Обратите внимание: это означает, что относительно небольшая дополнительная дельта-v выше, чем необходимо для ускорения до скорости убегания, получается относительно большая скорость на бесконечности. Например, в месте, где скорость эвакуации составляет 11,2 км / с, прибавление 0,4 км / с дает гиперболическую избыточную скорость 3,02 км / с.
Радиальная гиперболическая траектория
Релятивистская проблема двух тел
В контексте задача двух тел в общей теории относительности, траектории объектов с достаточной энергией, чтобы избежать гравитационного притяжения другого, больше не имеют формы гиперболы. Тем не менее, термин «гиперболическая траектория» все еще используется для описания орбит этого типа.
В астродинамика или же небесная механика, а гиперболическая траектория это траектория любого объекта вокруг центральный орган с более чем достаточной скоростью, чтобы избежать гравитационного воздействия центрального объекта. Название происходит от того, что согласно Ньютоновская теория такая орбита имеет форму гипербола. В более технических терминах это может быть выражено условием, что орбитальный эксцентриситет больше единицы.
Согласно упрощенным предположениям, тело, движущееся по этой траектории, будет двигаться к бесконечности, устанавливая конечную избыточную скорость относительно центрального тела. Аналогично параболические траектории, все гиперболические траектории также траектории ухода. В удельная энергия орбиты гиперболической траектории положительна.
Планетарные облеты, используемые для гравитационные рогатки, можно описать в пределах планеты сфера влияния с использованием гиперболических траекторий.
Содержание
Параметры, описывающие гиперболическую траекторию
Подобно эллиптической орбите, гиперболическая траектория для данной системы может быть определена (без учета ориентации) ее большой полуосью и эксцентриситетом. Однако для гиперболической орбиты другие параметры могут быть более полезными для понимания движения тела. В следующей таблице перечислены основные параметры, описывающие путь тела, следующего по гиперболической траектории вокруг другого при стандартных предположениях, и формулы, связывающие их.
Большая полуось, энергия и гиперболическая избыточная скорость
Обратите внимание, что полная энергия положительна в случае гиперболической траектории (тогда как она отрицательна для эллиптической орбиты).
Эксцентриситет и угол между заходом на посадку и вылетом
Параметр удара и дальность максимального сближения
В прицельный параметр это расстояние, на которое тело, если бы оно продолжало двигаться невозмущенным путем, могло бы пропустить центральное тело на своем ближайший подход. Для тел, испытывающих гравитационные силы и следующих по гиперболическим траекториям, он равен малой полуоси гиперболы.
В ситуации, когда космический корабль или комета приближается к планете, прицельный параметр и избыточная скорость будут известны точно. Если центральное тело известно, то теперь можно определить траекторию, включая то, насколько близко приближающееся тело будет в перицентре. Если он меньше радиуса планеты, следует ожидать удара. Расстояние наибольшего сближения или перицентрическое расстояние определяется как:
Итак, если приближается комета земной шар (эффективный радиус
6400 км) со скоростью 12,5 км / с (примерная минимальная скорость сближения тела, идущего с внешней стороны). Солнечная система), чтобы избежать столкновения с Землей, параметр удара должен быть не менее 8600 км, или на 34% больше радиуса Земли. Тело приближается Юпитер (радиус 70000 км) от внешней части Солнечной системы со скоростью 5,5 км / ч, во избежание столкновения потребуется, чтобы параметр удара был не менее 770 000 км или в 11 раз больше радиуса Юпитера.
Если масса центрального тела неизвестна, его стандартный гравитационный параметр и, следовательно, его масса могут быть определены путем отклонения меньшего тела вместе с параметром удара и скоростью приближения. Поскольку обычно все эти переменные могут быть определены точно, пролет космического корабля даст хорошую оценку массы тела.
Уравнения движения
Позиция
Связь между истинной аномалией θ и эксцентрическая аномалия E (в качестве альтернативы гиперболическая аномалия ЧАС) является: [2]
Средняя аномалия пропорциональна времени
Угол траектории полета
Скорость
Обратите внимание: это означает, что относительно небольшая дополнительная дельта-v выше, чем необходимо для ускорения до скорости убегания, получается относительно большая скорость на бесконечности. Например, в месте, где скорость эвакуации составляет 11,2 км / с, прибавление 0,4 км / с дает гиперболическую избыточную скорость 3,02 км / с.
Радиальная гиперболическая траектория
Релятивистская проблема двух тел
В контексте задача двух тел в общей теории относительности, траектории объектов с достаточной энергией, чтобы избежать гравитационного притяжения другого, больше не имеют формы гиперболы. Тем не менее, термин «гиперболическая траектория» все еще используется для описания орбит этого типа.
В астродинамика или же небесная механика, а гиперболическая траектория это траектория любого объекта вокруг центральный орган с более чем достаточной скоростью, чтобы избежать гравитационного воздействия центрального объекта. Название происходит от того, что согласно Ньютоновская теория такая орбита имеет форму гипербола. В более технических терминах это может быть выражено условием, что орбитальный эксцентриситет больше единицы.
Согласно упрощенным предположениям, тело, движущееся по этой траектории, будет двигаться к бесконечности, устанавливая конечную избыточную скорость относительно центрального тела. Аналогично параболические траектории, все гиперболические траектории также траектории ухода. В удельная энергия орбиты гиперболической траектории положительна.
Планетарные облеты, используемые для гравитационные рогатки, можно описать в пределах планеты сфера влияния с использованием гиперболических траекторий.
Содержание
Параметры, описывающие гиперболическую траекторию
Подобно эллиптической орбите, гиперболическая траектория для данной системы может быть определена (без учета ориентации) ее большой полуосью и эксцентриситетом. Однако для гиперболической орбиты другие параметры могут быть более полезными для понимания движения тела. В следующей таблице перечислены основные параметры, описывающие путь тела, следующего по гиперболической траектории вокруг другого при стандартных предположениях, и формулы, связывающие их.
Большая полуось, энергия и гиперболическая избыточная скорость
Обратите внимание, что полная энергия положительна в случае гиперболической траектории (тогда как она отрицательна для эллиптической орбиты).
Эксцентриситет и угол между заходом на посадку и вылетом
Параметр удара и дальность максимального сближения
В прицельный параметр это расстояние, на которое тело, если бы оно продолжало двигаться невозмущенным путем, могло бы пропустить центральное тело на своем ближайший подход. Для тел, испытывающих гравитационные силы и следующих по гиперболическим траекториям, он равен малой полуоси гиперболы.
В ситуации, когда космический корабль или комета приближается к планете, прицельный параметр и избыточная скорость будут известны точно. Если центральное тело известно, то теперь можно определить траекторию, включая то, насколько близко приближающееся тело будет в перицентре. Если он меньше радиуса планеты, следует ожидать удара. Расстояние наибольшего сближения или перицентрическое расстояние определяется как:
Итак, если приближается комета земной шар (эффективный радиус
6400 км) со скоростью 12,5 км / с (примерная минимальная скорость сближения тела, идущего с внешней стороны). Солнечная система), чтобы избежать столкновения с Землей, параметр удара должен быть не менее 8600 км, или на 34% больше радиуса Земли. Тело приближается Юпитер (радиус 70000 км) от внешней части Солнечной системы со скоростью 5,5 км / ч, во избежание столкновения потребуется, чтобы параметр удара был не менее 770 000 км или в 11 раз больше радиуса Юпитера.
Если масса центрального тела неизвестна, его стандартный гравитационный параметр и, следовательно, его масса могут быть определены путем отклонения меньшего тела вместе с параметром удара и скоростью приближения. Поскольку обычно все эти переменные могут быть определены точно, пролет космического корабля даст хорошую оценку массы тела.
Уравнения движения
Позиция
Связь между истинной аномалией θ и эксцентрическая аномалия E (в качестве альтернативы гиперболическая аномалия ЧАС) является: [2]
Средняя аномалия пропорциональна времени
Угол траектории полета
Скорость
Обратите внимание: это означает, что относительно небольшая дополнительная дельта-v выше, чем необходимо для ускорения до скорости убегания, получается относительно большая скорость на бесконечности. Например, в месте, где скорость эвакуации составляет 11,2 км / с, прибавление 0,4 км / с дает гиперболическую избыточную скорость 3,02 км / с.
Радиальная гиперболическая траектория
Релятивистская проблема двух тел
В контексте задача двух тел в общей теории относительности, траектории объектов с достаточной энергией, чтобы избежать гравитационного притяжения другого, больше не имеют формы гиперболы. Тем не менее, термин «гиперболическая траектория» все еще используется для описания орбит этого типа.
В астродинамика или же небесная механика, а гиперболическая траектория это траектория любого объекта вокруг центральный орган с более чем достаточной скоростью, чтобы избежать гравитационного воздействия центрального объекта. Название происходит от того, что согласно Ньютоновская теория такая орбита имеет форму гипербола. В более технических терминах это может быть выражено условием, что орбитальный эксцентриситет больше единицы.
Согласно упрощенным предположениям, тело, движущееся по этой траектории, будет двигаться к бесконечности, устанавливая конечную избыточную скорость относительно центрального тела. Аналогично параболические траектории, все гиперболические траектории также траектории ухода. В удельная энергия орбиты гиперболической траектории положительна.
Планетарные облеты, используемые для гравитационные рогатки, можно описать в пределах планеты сфера влияния с использованием гиперболических траекторий.
Содержание
Параметры, описывающие гиперболическую траекторию
Подобно эллиптической орбите, гиперболическая траектория для данной системы может быть определена (без учета ориентации) ее большой полуосью и эксцентриситетом. Однако для гиперболической орбиты другие параметры могут быть более полезными для понимания движения тела. В следующей таблице перечислены основные параметры, описывающие путь тела, следующего по гиперболической траектории вокруг другого при стандартных предположениях, и формулы, связывающие их.
Большая полуось, энергия и гиперболическая избыточная скорость
Обратите внимание, что полная энергия положительна в случае гиперболической траектории (тогда как она отрицательна для эллиптической орбиты).
Эксцентриситет и угол между заходом на посадку и вылетом
Параметр удара и дальность максимального сближения
В прицельный параметр это расстояние, на которое тело, если бы оно продолжало двигаться невозмущенным путем, могло бы пропустить центральное тело на своем ближайший подход. Для тел, испытывающих гравитационные силы и следующих по гиперболическим траекториям, он равен малой полуоси гиперболы.
В ситуации, когда космический корабль или комета приближается к планете, прицельный параметр и избыточная скорость будут известны точно. Если центральное тело известно, то теперь можно определить траекторию, включая то, насколько близко приближающееся тело будет в перицентре. Если он меньше радиуса планеты, следует ожидать удара. Расстояние наибольшего сближения или перицентрическое расстояние определяется как:
Итак, если приближается комета земной шар (эффективный радиус
6400 км) со скоростью 12,5 км / с (примерная минимальная скорость сближения тела, идущего с внешней стороны). Солнечная система), чтобы избежать столкновения с Землей, параметр удара должен быть не менее 8600 км, или на 34% больше радиуса Земли. Тело приближается Юпитер (радиус 70000 км) от внешней части Солнечной системы со скоростью 5,5 км / ч, во избежание столкновения потребуется, чтобы параметр удара был не менее 770 000 км или в 11 раз больше радиуса Юпитера.
Если масса центрального тела неизвестна, его стандартный гравитационный параметр и, следовательно, его масса могут быть определены путем отклонения меньшего тела вместе с параметром удара и скоростью приближения. Поскольку обычно все эти переменные могут быть определены точно, пролет космического корабля даст хорошую оценку массы тела.
Уравнения движения
Позиция
Связь между истинной аномалией θ и эксцентрическая аномалия E (в качестве альтернативы гиперболическая аномалия ЧАС) является: [2]
Средняя аномалия пропорциональна времени
Угол траектории полета
Скорость
Обратите внимание: это означает, что относительно небольшая дополнительная дельта-v выше, чем необходимо для ускорения до скорости убегания, получается относительно большая скорость на бесконечности. Например, в месте, где скорость эвакуации составляет 11,2 км / с, прибавление 0,4 км / с дает гиперболическую избыточную скорость 3,02 км / с.
Радиальная гиперболическая траектория
Релятивистская проблема двух тел
В контексте задача двух тел в общей теории относительности, траектории объектов с достаточной энергией, чтобы избежать гравитационного притяжения другого, больше не имеют формы гиперболы. Тем не менее, термин «гиперболическая траектория» все еще используется для описания орбит этого типа.