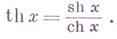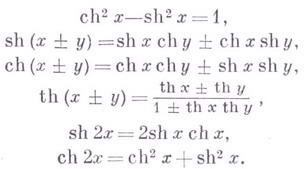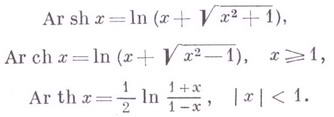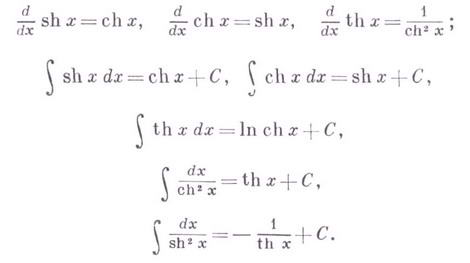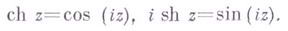Что такое гиперболические функции

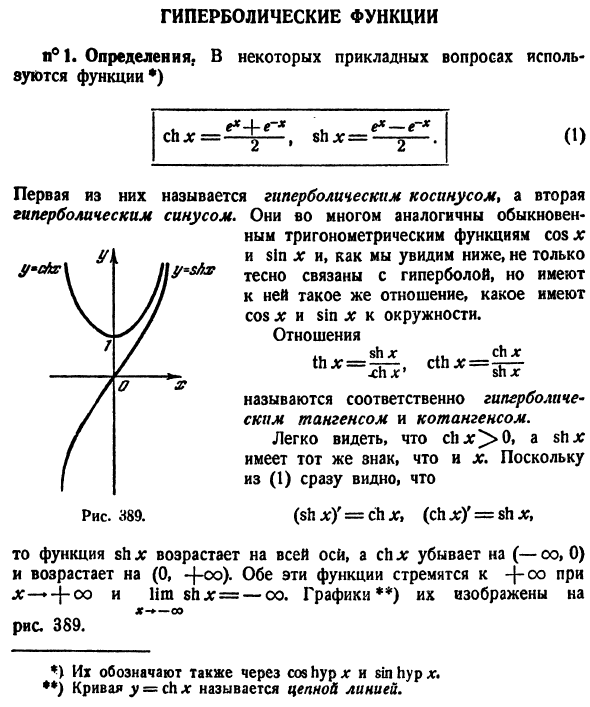
ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ

функции, определяемые формулами:

— гиперболический синус,

-г иперболический косинус.

Иногда рассматривается также гиперболический тангенс;

Другие обозначения: sinh x,Sh x,cosh x, Ch x,tgh x,tanh x,Th x. Графики см. на рис. 1.

Производные и основные интегралы от Г. ф.:

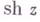
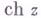
Во всей плоскости комплексного переменного z Г. ф. и могут быть определены рядами:

Полезное

Смотреть что такое «ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ» в других словарях:

Гиперболические функции — функции, определяемые формулами: (гиперболический синус), (гиперболический косинус). Иногда рассматривается также гиперболический тангенс: (графики Г. ф. см. на рис. 1). Г. ф.… … Большая советская энциклопедия

ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ — функции, определяемые формулами: (гиперболический синус), (гиперболический косинус), (гиперболический тангенс) … Большой Энциклопедический словарь

ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ — функции, определяемые формулами: shx = (ex e x)/2(гинерболич. синус), chх (еx + е к)/2 (гиперболич. косинус), thх = shx/chx (гиперболич. тангенс). Графики Г. ф. см. на рис … Естествознание. Энциклопедический словарь

Гиперболические функции — семейство элементарных функций, выражающихся через экспоненту и тесно связанных с тригонометрическими функциями. Содержание 1 Определение 1.1 Геометрическое определение … Википедия

гиперболические функции — функции, определяемые формулами: shx = (ex – e x)/2 (гиперболический синус), chx = (ex + e x)/2 (гиперболический косинус), thx = shx/chx (гиперболический тангенс). Графики гиперболических функций см. на рис. * * * ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ… … Энциклопедический словарь

ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ — Функции. определяемые ф лами: (гиперболич. синус), (гиперболич. косинус), (вставить рисунки. ) Графики гиперболических функций … Большой энциклопедический политехнический словарь

Гиперболические функции — По аналогии с тригонометрическими функциями Sinx, cosx, определяемыми, как известно, при помощи Эйлеровых формул sinx = (exi e xi)/2i, cosx = (exi + e xi)/2 (где е есть основание нэперовых логарифмов, a i = √[ 1]); иногда вводятся в рассмотрение… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Обратные гиперболические функции — функции, обратные по отношению к гиперболическим функциям (См. Гиперболические функции) sh х, ch х, th х; они выражаются формулами (читается: ареа синус гиперболический, ареа косинус гиперболический, ареа тангенс… … Большая советская энциклопедия

ОБРАТНЫЕ ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ — функции, обратные к гиперболич. функциям; выражаются формулами … Естествознание. Энциклопедический словарь

Обратные гиперболические функции — Обратные гиперболические функции определяются как обратные функции к гиперболическим функциям. Эти функции определяют площадь сектора единичной гиперболы x2 − y2 = 1 аналогично тому, как обратные тригонометрические функции определяют длину… … Википедия

Источник

Гиперболические функции

Гиперболи́ческие фу́нкции — семейство элементарных функций, выражающихся через экспоненту и тесно связанных с тригонометрическими функциями.

Содержание

Определение

Определение гиперболических функций через гиперболу

Один из способов определения тригонометрических функций через единичную окружность

Гиперболические функции задаются следующими формулами:

Существует сленговые названия: «шинус», «шимус»(?). Однако их использование не научно.

Существует сленговые названия: «чосинус», «кошинус». Однако их использование не научно.

Существует сленговые названия: «щангенс», «тахинус». Однако их использование не научно.

Иногда также определяются

Существует сленговые названия: «кочангенс», «кохинус». Однако их использование не научно.

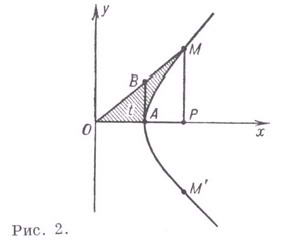
Геометрическое определение

Ввиду соотношения гиперболические функции дают параметрическое представление гиперболы (, ). При этом аргумент , где — площадь криволинейного треугольника , взятая со знаком «+», если сектор лежит выше оси , и «−» в противоположном случае. Это определение аналогично определению тригонометрических функций через единичную окружность, которое тоже можно построить подобным образом.

Свойства

Связь с тригонометрическими функциями

Гиперболические функции выражаются через тригонометрические функции от мнимого аргумента.

.

Важные тождества

Разложение в степенные ряды

Здесь — числа Бернулли.

Графики

Аналитические свойства

Гиперболический синус и гиперболический косинус аналитичны во всей комплексной плоскости, за исключением существенно особой точки на бесконечности. Гиперболический тангенс аналитичен везде, кроме полюсов в точках , где — целое. Вычеты во всех этих полюсах равны единице. Гиперболический котангенс аналитичен везде, кроме точек , вычеты его в этих полюсах также равны единице.

Обратные гиперболические функции

Читаются ареа… (-синус и т. д.) — от лат. «area» — «площадь».

— обратный гиперболический синус: — обратный гиперболический косинус — обратный гиперболический тангенс — обратный гиперболический котангенс — обратный гиперболический секанс 0\end>\right.>» /> — обратный гиперболический косеканс

Эти функции имеют следующее разложение в ряд:

1>» />

История

Гиперболические функции были введены Винченцо Риккати (Vincenzo Riccati) в 1757 году («Opusculorum», том I). Он получил их из рассмотрения единичной гиперболы.

Применение

Гиперболические функции часто встречаются при вычислении различных интегралов. Некоторые интегралы от рациональных функций и от функций, содержащих радикалы, довольно просто выполняются с помощью замен переменных с использованием гиперболических функций.

Ссылки

cs:Hyperbolická funkce he:פונקציות היפרבוליות hu:Hiperbolikus függvények is:Breiðbogafall nl:Hyperbolische functie pl:Funkcje hiperboliczne sr:Хиперболичне функције sv:Hyperbolisk funktion

Источник

Гиперболические функции

Содержание:

Гиперболические функции

Гиперболические функции — семейство элементарных функций, выражающихся через экспоненту и тесно связанных с тригонометрическими функциями.

Основные понятия:

Рассмотрим единичную окружность с центром в начале координат, уравнение которого имеет вид х 2 + у 2 = 1.

Согласно определению, синусом угла называют ординату у точки А(х, у) единичной окружности, а косинусом — абсциссу х этой же точки (рис. 1)

Докажем, что площадь сектора АОВ равна числовому значению угла AOD, взятом в радианах.

Действительно, если R=1, а угол сектора АОВ- то

Следовательно, в тригонометрических функциях за аргумент можно принимать не только угол, а и площадь соответствующего сектора.

Рассмотрим теперь равнобокую гиперболу с асимптотами , уравнение которой имеет вид

Повторим предыдущие рассуждения:

— выберем на гиперболе т. А(х, у);

— проведём радиусы ОА и ОВ ().

Образовавшуюся фигуру OANB называют гиперболическим сектором (сектором ),

Возьмём за аргумент площадь гиперболического сектора . Получим:

Найдём площадь гиперболического сектора, как разность площади треугольника АОВ и криволинейной трапеции ANB.

Потому, что фигура симметрична, имеем

либо, решив систему

Аналогично как в тригонометрии вводят понятия тангенса и котангенса

Свойства гиперболических функций

Чётность и нечётность проверим подставив (-х) в соответствующие формулы

Следовательно, как и в тригонометрических функциях, имеем чётная, а нечётные.

Остальные свойства легко установить построив графики гиперболических функций.

Для построения воспользуемся записью

то есть графики функций

Полученные графическим сложением ординат графики функций имеют вид:

Графики следующие

Видим, что в отличии от тригонометрических, гиперболические функции непериодические. Основные свойства каждой из гиперболических функций указаны в опорном конспекте (п. 10.5).

Дифференцирование и интегрирование гиперболических функций

Гиперболические функции можно дифференцировать и интегрировать. Выведем формулы производных и интегралов.

Переход от гиперболических функций к тригонометрическим и наоборот

Используя гиперболические функции можно вывести формулы Эйлера. Действительно, вспомним разложение в ряд Маклорена функций

Положим в разложении функции у=е х за аргумент х=zj. Получим:

Учитывая, что где будем иметь:

Именно эти формулы позволяют установить зависимость между тригонометрическими и гиперболическими функциями.

Принимаем без доказательств, что все тригонометрические формулы действительны и для воображаемого аргумента. Это предположение позволит установить зависимость между гиперболическими функциями.

Аналогично можно получить формулы для

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник

Гиперболические функции

Гиперболические функции

Каждое тригонометрическое выражение имеет нечто похожее на теорию гиперболических функций. Людмила Фирмаль

Связь с гиперболой. x = cos t, y = sin t (4) Представляет параметрическое уравнение окружности jc * — <- y * = 1. х = й, у = шт. Людмила Фирмаль

Для кругов ch t и sh t играют ту же роль, что и cos t и sin t. Указанные связи между функциями ch t и sh t и гиперболой носят несколько формальный характер. Изучите эту связь подробно. По этой причине (рис. 390) площадь кругового сектора при угле AOM = t Поскольку AOM равен, вы можете написать: Правила.

Чтобы создать стоимость и грех на рисунке, вы должны найти по кругу Точка M (xt y), где площадь сектора AOM равна y. Далее x = cos t, y = sin t. Используя похожие правила, вы можете создавать ch t и sh t. Чтобы установить это, рассмотрим точку M (X, y) на правой ветви a Рис. 390 М / JBM o A 9 Рисунок 391. Xb — y гипербола ss 1. Для ясности пусть 5> 0 (рис. 391). Найдите область F в секторе АОМ.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Гипербола: определение, функция, формула, примеры построения

В данной публикации мы рассмотрим, что такое гипербола, приведем формулу, с помощью которой задается ее функция, а также на практических примерах разберем алгоритм построения данного вида графика.

Определение и функция гиперболы

Гипербола – это график функции обратной пропорциональности, которая в общем виде задается следующей формулой:

Пример 1

Дана функция y = 4 /_x. Построим ее график.

Решение

Так как k > 0, следовательно, гипербола будет находиться в I и III координатных четвертях.

Чтобы построить график, сначала нужно составить таблицу соответствия значений x и y. То есть мы берем конкретное значение x, подставляем его в формулу функции и получаем y.

» data-lang=»default» data-override=»<"emptyTable":"","info":"","infoEmpty":"","infoFiltered":"","lengthMenu":"","search":"","zeroRecords":"","exportLabel":"","file":"default">» data-merged=»[]» data-responsive-mode=»2″ data-from-history=»0″>

0,5

8

1

4

2

2

4

1

8

0,5

Чтобы построить ветвь в третьей четверти, вместо x в формулу подставляем -x. Так мы вычислим значения y. Соединив полученные точки получаем следующий результат. На этом построение гиперболы завершено. Пример 2 Рассмотренный выше пример был одним из самых простых (без смещения асимптот). Давайте усложним задачу и построим гиперболу, заданную функцией ниже: Источник ← Что такое плагин не установлен в личном кабинете налоговой Что такое перехватывающая автостоянка → Вам также понравится Что такое гарантирующая организация 27.10.202314.04.2022 admin 0 Что такое мхл в хоккее расшифровка 26.10.202317.04.2022 admin 0 Что такое мягкий хэндовер 26.10.202317.04.2022 admin 0 Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сохранить моё имя, email и адрес сайта в этом браузере для последующих моих комментариев.