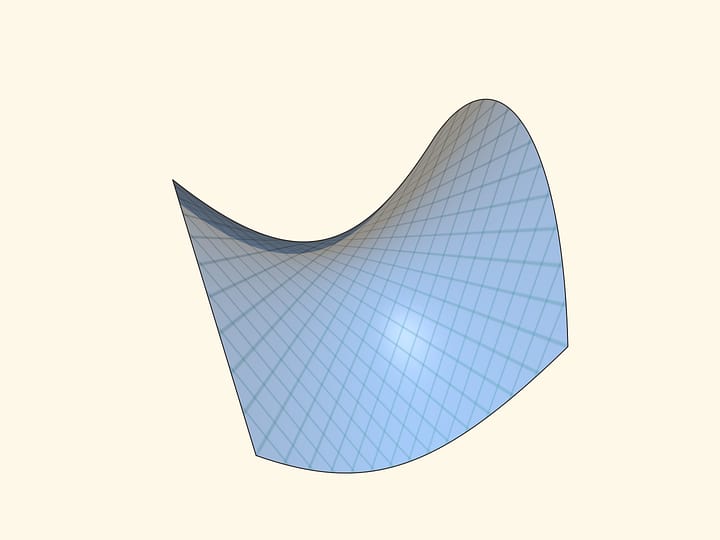
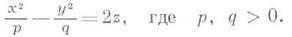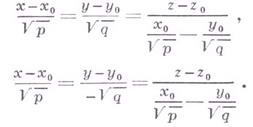Что такое гиперболический параболоид

Параболический гиперболоид

Параболо́ид ― тип поверхности второго порядка. Параболоид может быть охарактеризован как незамкнутая нецентральная (т.е. не имеющая центра симметрии) поверхность второго порядка.

Канонические уравнения параболоида в декартовых координатах:

Содержание

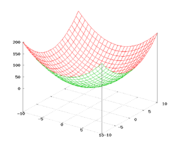
Эллиптический параболоид

Эллипти́ческий параболо́ид — поверхность, описываемая функцией вида

,

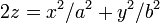
где a и b одного знака. Поверхность описывается семейством параллельных парабол с ветвями, направленными вверх, вершины которых описывают параболу, с ветвями, также направленными вверх.

Если a = b то эллиптический параболоид представляет собой поверхность вращения, образованную вращением параболы вокруг вертикальной оси, проходящей через вершину данной параболы.

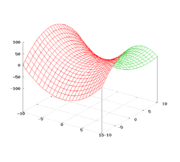
Гиперболический параболоид

Гиперболи́ческий параболо́ид (называемый в строительстве «гипар») — седлообразная поверхность, описываемая в прямоугольной системе координат уравнением вида

.

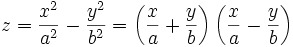
Из второго представления видно, что гиперболический параболоид является линейчатой поверхностью.

Поверхность может быть образована движением параболы, ветви которой направлены вниз, по параболе, ветви которой направлены вверх, при условии, что первая парабола соприкасается со второй своей вершиной.

Параболоиды в мире

В технике

В искусстве

В литературе

Устройство, описанное в Гиперболоид инженера Гарина должно было быть параболоидом.

Полезное

Смотреть что такое «Параболический гиперболоид» в других словарях:

ПОВЕРХНОСТЬ ВТОРОГО ПОРЯДКА — множество точек 3 мерного действительного (или комплексноро) пространства, координаты к рых в декартовой системе удовлетворяют алгебраич. уравнению 2 й степени (*) Уравнение (*) может и не определять действительного геометрич. образа, в таких… … Математическая энциклопедия

Поверхность второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида в котором по крайней мере один из коэффициентов … Википедия

Поверхности второго порядка — Поверхность второго порядка геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида a11x2 + a22y2 + a33z2 + 2a12xy + 2a23yz + 2a13xz + 2a14x + 2a24y + 2a34z + a44 = 0 в котором по крайней мере один из… … Википедия

Коноид — тело, образуемое вращением какой нибудь кривой линии около неподвижной оси; так может быть К. параболический или параболоид вращения, К. гиперболический или гиперболоид вращения и пр. Сечение К. плоскостью перпендикулярно оси обычно круг, но… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Источник

ГИПЕРБОЛИЧЕСКИЙ ПАРАБОЛОИД

незамкнутая нецентральная поверхность второго порядка. В надлежащей системе координат (см. рис.) уравнение Г. п. имеет вид:

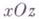
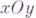
Сечения Г. п. плоскостями, параллельными плоскостям и , являются параболами, а сечения плоскостями, параллельными плоскости ,- гиперболами (плоскостью — двумя прямыми). Ось симметрии Т. п. наз. его осью; точка пересечения Г. п. с осью наз. вершиной Г. п. Если p = q, то Г. п. имеет две оси симметрии. Г. п.- линейчатая поверхность;

уравнения прямолинейных образующих, проходящих через данную точку 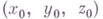Г. п., имеют вид:

Смотреть что такое «ГИПЕРБОЛИЧЕСКИЙ ПАРАБОЛОИД» в других словарях:

ГИПЕРБОЛИЧЕСКИЙ ПАРАБОЛОИД — один из двух типов параболоидов … Большой Энциклопедический словарь

гиперболический параболоид — один из двух типов параболоидов. * * * ГИПЕРБОЛИЧЕСКИЙ ПАРАБОЛОИД ГИПЕРБОЛИЧЕСКИЙ ПАРАБОЛОИД, один из двух типов параболоидов (см. ПАРАБОЛОИДЫ) … Энциклопедический словарь

Гиперболический параболоид — один из двух видов параболоидов (См. Параболоиды) … Большая советская энциклопедия

Гиперболический параболоид — см. Косая плоскость … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

ГИПЕРБОЛИЧЕСКИЙ ПАРАБОЛОИД — один из двух типов параболоидов … Естествознание. Энциклопедический словарь

Гиперболический параболоид — форма крыши, имеющая двойную кривизну. (Архитектура: иллюстрированный справочник, 2005) … Архитектурный словарь

ПАРАБОЛОИД — ПАРАБОЛОИД, параболоида, муж. (см. парабола) (мат.). Поверхность второго порядка, не имеющая центра. Параболоид вращения (образуется вращением параболы вокруг ее оси). Эллиптический параболоид. Гиперболический параболоид. Толковый словарь Ушакова … Толковый словарь Ушакова

ПАРАБОЛОИД — ПАРАБОЛОИД, поверхность, получаемая при движении параболы, вершина которой скользит по другой, неподвижной параболе (с осью симметрии, параллельной оси движущейся параболы), тогда как ее плоскость, смещаясь параллельно самой себе, остается… … Современная энциклопедия

Параболоид — ― тип поверхности второго порядка. Параболоид может быть охарактеризован как незамкнутая нецентральная (то есть не имеющая центра симметрии) поверхность второго порядка. Канонические уравнения параболоида в декартовых координатах: если и одного… … Википедия

Источник

Седловидная поверхность: гиперболический параболоид ⁠

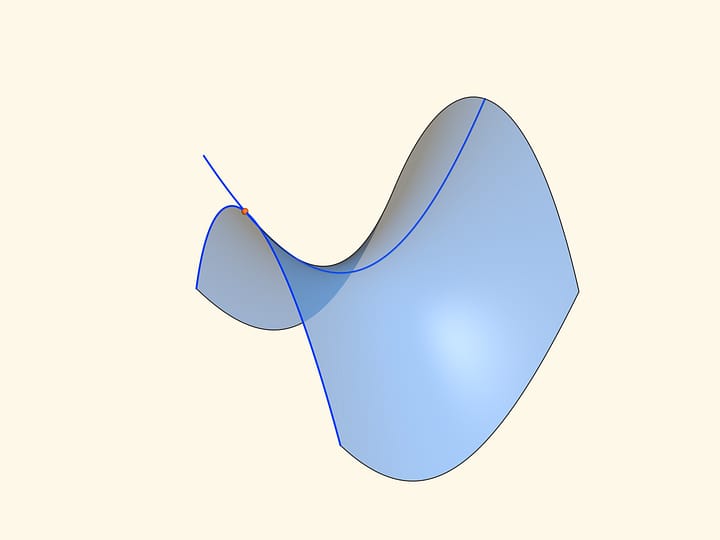
Гипер­бо­ли­че­ский пара­бо­лоид — поверх­ность, напоми­нающая седло. Она обра­зу­ется при таком движе­нии пара­болы с вет­вями вниз, что её вершина сколь­зит по дру­гой, непо­движ­ной пара­боле с вет­вями вверх. Плос­ко­сти пара­бол в каж­дый момент времени перпен­ди­ку­лярны, оси парал­лельны.

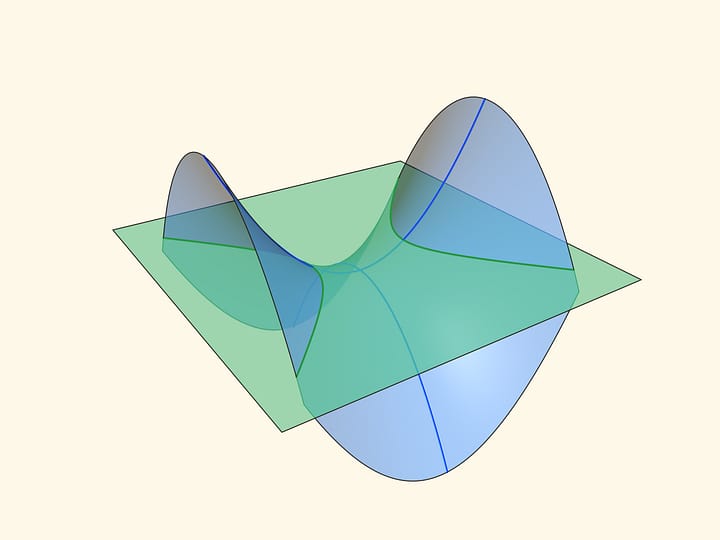
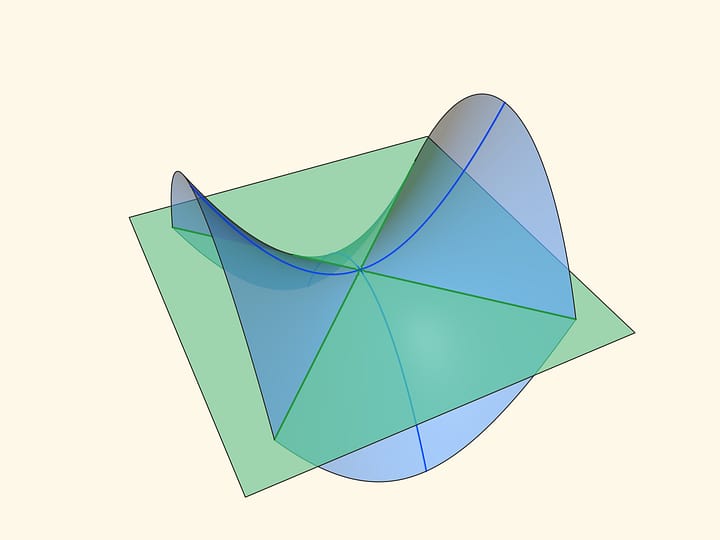
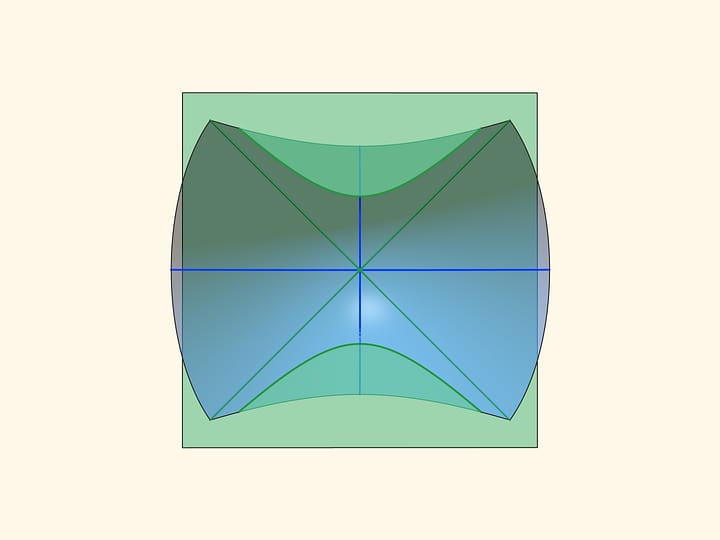
При пере­се­че­нии гипер­бо­ли­че­ского пара­бо­ло­ида с любой гори­зон­таль­ной плос­ко­стью полу­ча­ется гипер­бола. Если плос­кость про­хо­дит через центр седла, то гипер­бола вырож­да­ется в пару пере­се­кающихся прямых. (Если на эту плос­кость спро­еци­ро­вать гипер­болу из парал­лель­ного сече­ния, то прямые будут асимп­то­тами гипер­бо­лы‐про­екции.)

Ока­зы­ва­ется, гипер­бо­ли­че­ский пара­бо­лоид — линей­ча­тая поверх­ность, она также может быть обра­зо­вана движе­нием прямой линии!

Между двумя парал­лель­ными прямыми через рав­ные рас­сто­я­ния пустим набор отрез­ков. Повер­нём прямые вокруг цен­траль­ного отрезка в раз­ные сто­роны. (При этом длины всех отрез­ков, кроме цен­траль­ного, изме­нятся.) Так рас­по­ложен­ные в про­стран­стве отрезки лежат на гипер­бо­ли­че­ском пара­бо­ло­иде.

Эта поверх­ность допус­кает кра­си­вую реа­ли­за­цию в виде модели из тру­бо­чек.

Гаус­сова кри­визна во всех точ­ках гипер­бо­ли­че­ского пара­бо­ло­ида отрица­тельна. Такие поверх­но­сти назы­вают сед­ло­выми из-за визу­аль­ного сход­ства с сед­лом для вер­хо­вой езды.

Источник

Параболоид

В этом положении гиперболический параболоид открывается вниз по оси x и вверх по оси y (то есть парабола в плоскости x = 0 открывается вверх, а парабола в плоскости y = 0 открывается вниз).

СОДЕРЖАНИЕ

Свойства и приложения [ править ]

Эллиптический параболоид [ править ]

В подходящей декартовой системе координат эллиптический параболоид имеет уравнение

Очевидно, круговой параболоид содержит круги. Это верно и в общем случае (см. Раздел Циркуляр ).

Плоские сечения эллиптического параболоида могут быть:

Параболический отражатель [ править ]

Поэтому форма круглого параболоида широко используется в астрономии для параболических отражателей и параболических антенн.

Поверхность вращающейся жидкости также представляет собой круговой параболоид. Это используется в телескопах с жидкостными зеркалами и в изготовлении твердых зеркал телескопов (см. Вращающуюся печь ).

Параллельные лучи, попадающие в круглое параболоидальное зеркало, отражаются к фокусной точке F или наоборот.

Вращающаяся вода в стакане

Гиперболический параболоид [ править ]

Это свойство упрощает изготовление гиперболического параболоида из различных материалов и для различных целей, от бетонных крыш до закусок. В частности, жареные закуски Pringles напоминают усеченный гиперболический параболоид. [4]

Плоское сечение гиперболического параболоида с уравнением

Поверхность, изображающая гиперболический параболоид

Restaurante Los Manantiales, Сочимилько, Мексика

Цилиндр между карандашами эллиптических и гиперболических параболоидов [ править ]

Карандаш эллиптического параболоида

и пучок гиперболических параболоидов

подходить к той же поверхности

Кривизна [ править ]

Эллиптический параболоид, параметризованный просто как

имеет гауссову кривизну

и средняя кривизна

которые всегда положительны, имеют максимум в начале координат, становятся меньше по мере удаления точки на поверхности от начала координат и асимптотически стремятся к нулю по мере того, как указанная точка бесконечно удаляется от начала координат.

Гиперболический параболоид [2], параметризованный как

имеет гауссову кривизну

и средняя кривизна

Геометрическое представление таблицы умножения [ править ]

Если гиперболический параболоид

z = x 2 a 2 − y 2 b 2 <\displaystyle z=<\frac >>>-<\frac >>>>

поворачивается на угол π / 4 в направлении + z (согласно правилу правой руки ) результатом является поверхность

z = ( x 2 + y 2 2 ) ( 1 a 2 − 1 b 2 ) + x y ( 1 a 2 + 1 b 2 ) <\displaystyle z=\left(<\frac +y^<2>><2>>\right)\left(<\frac <1>>>-<\frac <1>>>\right)+xy\left(<\frac <1>>>+<\frac <1>>>\right)>

и если a = b, то это упрощается до

Две параболоидальные ℝ 2 → функции

являются гармонически сопряженными и вместе образуют аналитическую функцию

Размеры параболоидальной тарелки [ править ]

Размеры симметричной параболоидальной тарелки связаны уравнением

Объем блюда, количество жидкости, которое оно могло бы удержать, если бы край был горизонтальным, а вершина находилась на дне (например, вместимость параболоидального вок ), определяется выражением

Источник

Что такое гиперболический параболоид

Гиперболоидную форму конструкций ввёл в архитектуру В. Г. Шухов (патент Российской Империи № 1896; от 12 марта 1899 года, заявленный В. Г. Шуховым 11.01.1896). Первая в мире стальная сетчатая башня в форме гиперболоида вращения была построена Шуховым для крупнейшей дореволюционной Всероссийской промышленной и художественной выставки в Нижнем Новгороде, проходившей с 28 мая (9 июня) по 1 (13) октября 1896 года.

Однополостный гиперболоид вращения первой башни Шухова образован 80 прямыми стальными профилями, концы которых крепятся к кольцевым основаниям. Сетчатая стальная оболочка из ромбовидно пересекающихся профилей упрочнена 8 параллельными стальными кольцами, расположенными между основаниями. Высота гиперболоидной оболочки башни — 25,2 метра (без учёта высот фундамента, резервуара и надстройки для обозрения).

Диаметр нижнего кольцевого основания — 10,9 метра, верхнего — 4,2 метра. Максимальный диаметр бака — 6,5 метра, высота — 4,8 метра. От уровня земли из центра основания башни до уровня дна резервуара поднимается красивая стальная винтовая лестница. В центральной части бак имеет цилиндический проход с прямой лестницей, ведущей на смотровую площадку на верхней поверхности резервуара.

Над смотровой площадкой на баке сделана гиперболоидная надстройка с прямой лёгкой лестницей, ведущей на более высокую малую смотровую площадку. Гиперболоидная надстройка смонтирована из 8 прямых профилей, упирающихся в кольцевые основания, между которыми расположено ещё одно упрочняющее кольцо. Верхняя площадка в 1896 году имела деревянный настил и ограждение (не сохранились до настоящего времени). Общая высота башни составляет 37 метров. Все стальные элементы конструкции башни соединены заклёпками.

После выставки первая башня Шухова была перенесена в имение мецената Ю. С. Нечаева-Мальцова в село Полибино Данковского района Липецкой области. Башня сохранилась до нашего времени, является памятником архитектуры, охраняется государством. Первая в мире гиперболоидная конструкция страдает от коррозии и нуждается в реставрации.

В начале 20-го века многие боевые корабли, в основном в США, строились с ажурными гиперболоидными мачтами.

Такое решение объясняется необходимостью размещения большого объёма наблюдательных и дальномерных приборов на большой высоте от палубы, меньшей уязвимостью в бою и амортизацией ударов от отдачи собственных, очень мощных, орудий.

Дальнейшей модификацией идеи сетчатых гиперболоидных конструкций стала конструкция радиобашни на Шаболовке в Москве, построенной Шуховым в 1919—1922 гг. Первоначальный проект высотой 350 м из-за дефицита металла был заменен на 150-метровый вариант, который эксплуатируется и поныне. В течение своей жизни Шухов построил более двухсот гиперболоидных башен различного назначения.

Гиперболоидные конструкции впоследствии строили многие великие архитекторы: Гауди, Ле Корбюзье, Оскар Нимейер.

Гиперболоидные шуховские башни востребованы и в настоящее время. В 1963 году в порту города Кобе в Японии по проекту компании Nikken Sekkei (недоступная ссылка) была построена 108-метровая гиперболоидная шуховская башня (Kobe Port Tower).

А в 1968 году в Чехии по проекту архитектора Карела Хубачека была построена гиперболидная башня «Йештед» высотой 100 метров. В 2003 году была построена гиперболоидная башня Шухова в Цюрихе. Авторы башни — архитекторы Даниэль Рот и Александр Ком (Daniel Roth, Alexander Kohm). Идеи гиперболоидных конструкций башен Шухова известный архитектор Михаил Посохин предложил использовать при проектировании новых небоскрёбов в деловом центре «Москва-Сити».

600-метровая гиперболоидная сетчатая шуховская башня построена в 2010 году в Гуанчжоу в Китае компанией Arup. На 2017 год это вторая по высоте башня в мире.

Гиперболоид

В математике гиперболоид — это вид поверхности второго порядка в трёхмерном пространстве, задаваемый в декартовых координатах уравнением

где a и b — действительные полуоси, а c — мнимая полуось;

где a и b — мнимые полуоси, а c — действительная полуось.

Если a = b, то такая поверхность называется гиперболоидом вращения. Однополостный гиперболоид вращения может быть получен вращением гиперболы вокруг её мнимой оси, двуполостный — вокруг действительной. Двуполостный гиперболоид вращения также является геометрическим местом точек P, модуль разности расстояний от которых до двух заданных точек A и B постоянен: | AP — BP | = const

В этом случае A и B называются фокусами гиперболоида.

Однополостный гиперболоид является дважды линейчатой поверхностью; если он является гиперболоидом вращения, то он может быть получен вращением прямой вокруг другой прямой, скрещивающейся с ней.

В сечении однополостного гиперболоида плоскостью можно получить кривую любого эксцентриситета (e) от нуля до бесконечности.

Параболоид

Параболо́ид ― тип поверхности второго порядка в трёхмерном евклидовом пространстве.

Параболоид может быть охарактеризован как незамкнутая нецентральная (то есть не имеющая центра симметрии) поверхность второго порядка.

Канонические уравнения параболоида в декартовых координатах:

где t и u — действительные числа не равные нулю одновременно.

если t и u одного знака, то параболоид называется эллиптическим, частный случай эллиптического параболоида t = u в этом случае поверхность принято называть параболоидом вращения;
Далее, если t и u разного знака, то параболоид называется гиперболическим;
если один из коэффициентов равен нулю, то параболоид называется параболическим цилиндром.
Cечения параболоида вертикальными (параллельными оси z) плоскостями произвольного положения — параболы.

Сечения параболоида горизонтальными плоскостями, параллельными плоскости x\ y для эллиптического параболоида — эллипсы, для параболоида вращения эти пересечения — окружности, когда такое пересечение существует.

Пересечения для гиперболического параболоида — гиперболы.

В частных случаях пересечения, сечением может оказаться прямая или пара прямых (для гиперболического параболоида или пара параллельных прямых для параболического цилиндра) или вырождаться в одну точку (для эллиптического параболоида).

Материал из Википедии — свободной энциклопедии.

Источник